一类执行器偏移/卡死故障下的自适应容错控制

金小峥

一类执行器偏移/卡死故障下的自适应容错控制

金小峥

(沈阳大学 装备制造综合自动化辽宁省重点实验室,辽宁 沈阳 110044)

研究执行器故障下的连续时不变线性系统主动容错控制问题.考虑执行器部分失效和偏移/卡死故障,并假设偏移/卡死故障可以被分为状态依赖时变部分和常值偏移部分,且状态依赖权值和常值偏移量未知.设计自适应律在线故障执行器失效因子和状态依赖权重与常值偏移/卡死量,并基于自适应估计值构造状态反馈控制增益方程补偿故障带来的影响.通过李亚普诺夫第二稳定性定理,证明所提出的自适应容错控制策略能够保证系统在执行器故障情况下渐近稳定.最后,通过数值实例显示了该方法的有效性.

容错控制;状态反馈;执行器;偏移/卡死故障;自适应控制

容错控制技术是一种提高系统的可靠性与安全性的关键控制技术.容错控制系统的特点表现在当系统执行器、传感器、对象本身及其他系统元部件发生故障时,系统的安全运行仍然能够得到保障并保持满意性能.在过去40多年的发展中,学者们将容错控制方法分为被动控制方法和主动控制方法.基于鲁棒控制技术的被动容错控制对预先给定的故障模式设计固定增益控制器,使系统的反馈对预知的故障起到不敏感的作用并优化不同故障模式下的性能.而通过在线调节控制策略的主动容错控制补偿故障所带来的影响,使系统稳定并保持满意性能.不同于故障诊断方法需要诊断机构提供较为精确的故障诊断信号,主动容错方法中的自适应方法不需要自适应机构精确估计故障,从而不会产生故障误诊导致容错失败.由于自适应技术可以提供未知参数的每一个瞬间估计,并且可以使控制增益以最快的速度响应测量参数的变化,这一特征针对故障的未知性,以及控制系统的实时鲁棒性和性能起着重要作用.因此,基于自适应技术的主动容错控制方法受到学者们的广泛关注.

在已有的容错控制研究中,针对执行器故障的研究已经取得了很多成果.文献[13]分别用线性矩阵不等式、代数Riccati方法和极点配置等被动容错控制方法对执行器的失效故障和中断故障进行了研究.许多学者提出不同的基于故障诊断检测(FDI)技术在线重构控制策略来达到容错目的,如文献[45].而在自适应容错控制系统设计中,针对执行器故障的容错控制研究也取得了较多成果.在这些文献中,多类执行器故障模型被学者们重点研究.文献[6]利用间接自适应方法研究了有执行器部分失效的飞行控制跟踪问题.文献[79]则设计了直接自适应控制律,保证系统在执行器参数化卡死情况下跟踪参考模型信号.文献[7]在非参数化卡死故障的界已知的条件下,得到了跟踪误差有界的结果.针对非参数化卡死故障,文献[1012]分别提出了直接自适应、间接自适应和切换自适应方法解决系统渐近稳定问题.文献[1314]则结合自适应方法和线性矩阵不等式方法,分别设计了状态反馈和动态输出反馈下的容错H∞补偿控制器,既补偿了故障,又优化了系统的性能.文献[15]也对自适应容错H∞问题有所研究.在主从大系统下,文献[16]针对执行器偏移故障研究了系统自适应同步问题.

本文将偏移/卡死故障的范数有界条件退化为依赖于系统状态部分和常值部分,针对这类执行器故障,提出自适应控制策略可以保证系统渐近稳定,并不会出现控制输入抖震现象.

1 系统描述

考虑连续时间线性时不变系统,其状态空间方法描述如下:

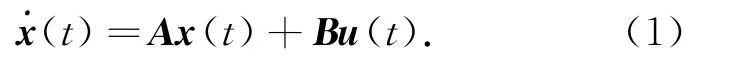
式中,x∈Rn表示系统状态,u∈Rm表示系统控制输入,矩阵A和B为有恰当维数的已知常矩阵.

本文考虑执行器出现失效和偏移故障,其故障模型描述如下:

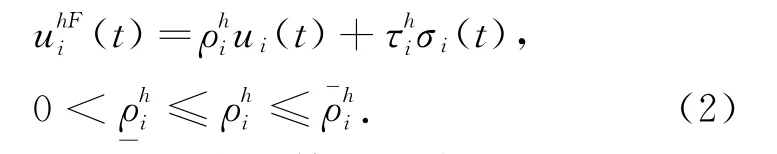
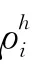
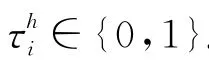
定义

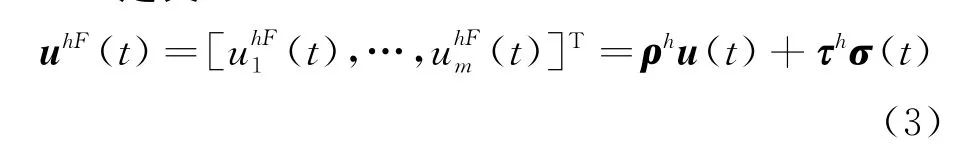
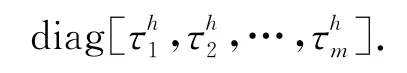
定义集合如下:

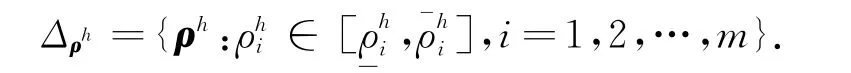
为描述方便,将对整个故障模式简写成

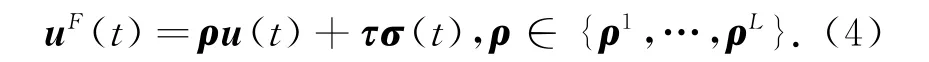
由此,系统(1)可以写成如下形式:

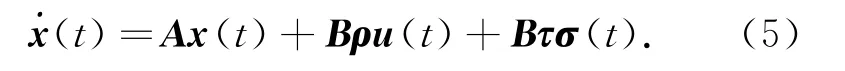
这里,假设偏移/卡死量σ(t)由时变部分σ1(t)和常值部分σ2组成,即:

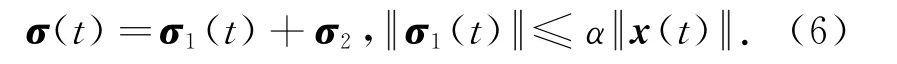
其中α为未知正常数.

为了解决执行器故障(4)下系统的渐近稳定问题,设计如下状态反馈控制器:

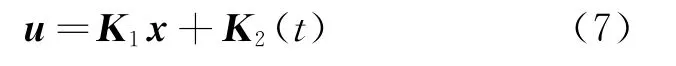
式中,K1∈Rm×n和K2∈Rm分别用来保证无执行器故障和有执行器故障下的系统的渐近稳定.

则将式(7)代人式(5),可以得到相应的闭环系统:

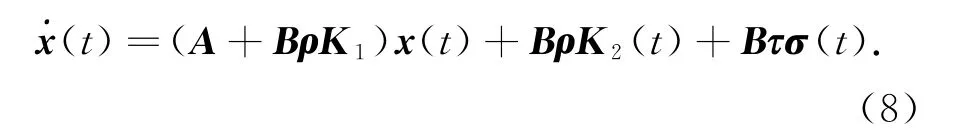
由此,本文的主要目标为构造控制器u(t)使得闭环系统(8)在执行器故障下渐近稳定.

2 自适应容错控制

式中,P∈Rn×n为正定矩阵.并假设存在一个足够大的正常数λ使得如下不等式成立:

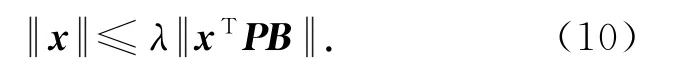
根据系统在正常情况和故障情况下的可控性,则对任意模式ρ∈Δρh存在一个正定矩阵Q∈Rn×n和恰当维数矩阵W使得如下线性矩阵不等式成立

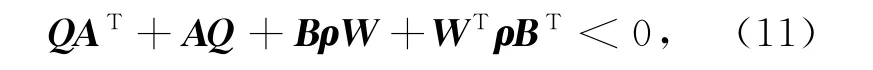
则控制增益矩阵K1=WQ-1.

另一方面,选取K2(t)为

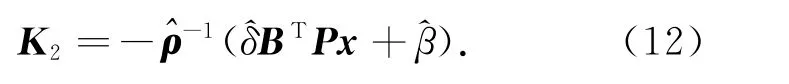
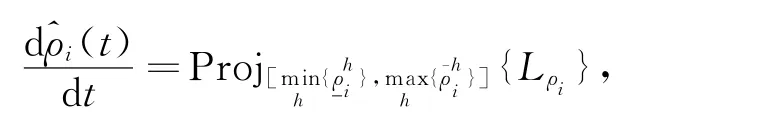
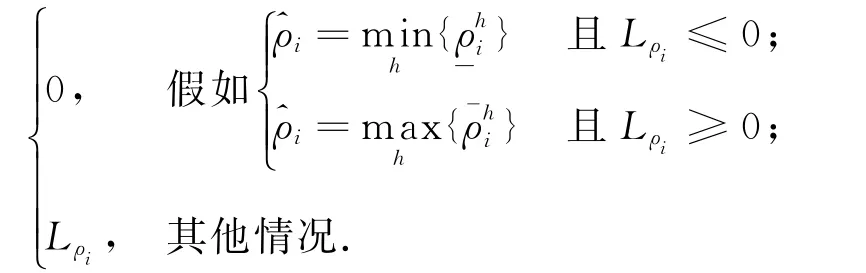
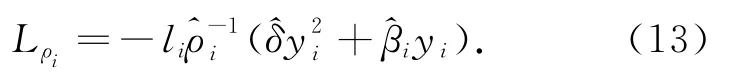
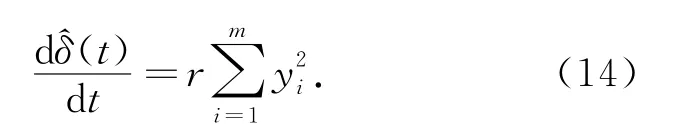
而^βi为未知常数βi=τiσ2i,i=1,2,…,m的估计值,由如下自适应律自动调节

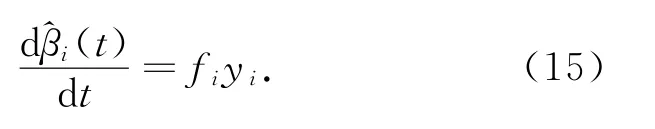
在上述三个自适应方程中,li,r和fi分别为自适应律(13)、(14)和(15)的权重,yi在式(9)中被定义.令

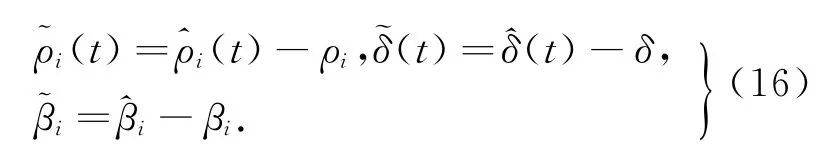
由于ρi,δ和βi均为常数,则有如下误差系统:

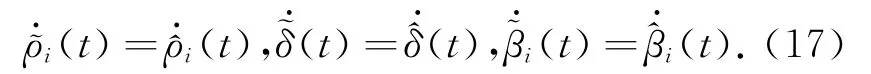
式中,i=1,2,…,m.

定理1 对闭环容错控制系统(8)和误差系统(17),假如式(11)有解,且采用式(12)所示的控制方程以及式(13)～式(15)的参数自适应律,则对任意的ρ∈Δρh闭环系统渐近稳定.

证明 选择如下所示的Lyapunov方程:

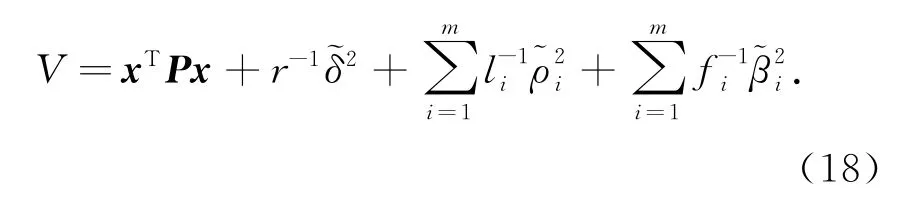
则对任意的ρ∈Δρh,式(18)沿闭环系统求导得到: ˙V(t)≤

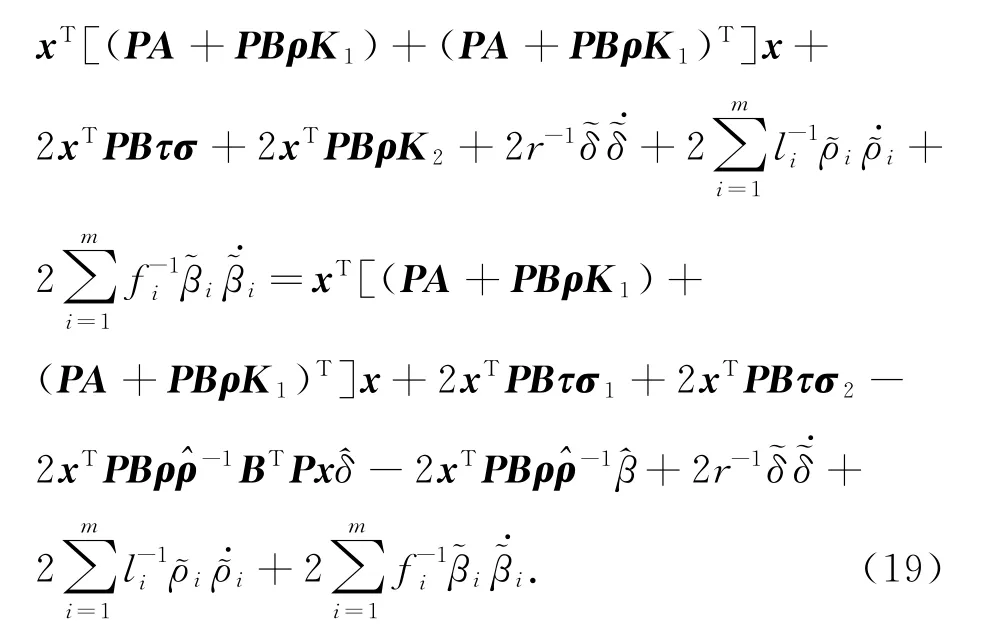
由于τhi∈{0,1}且根据不等式(6)、式(10)和等式(16),得到

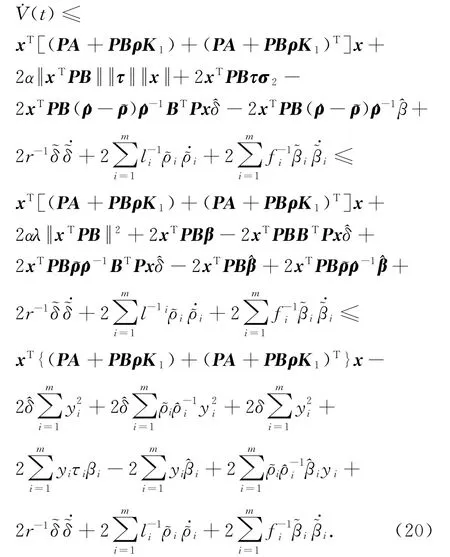
选取自适应律(13)～(15),则有

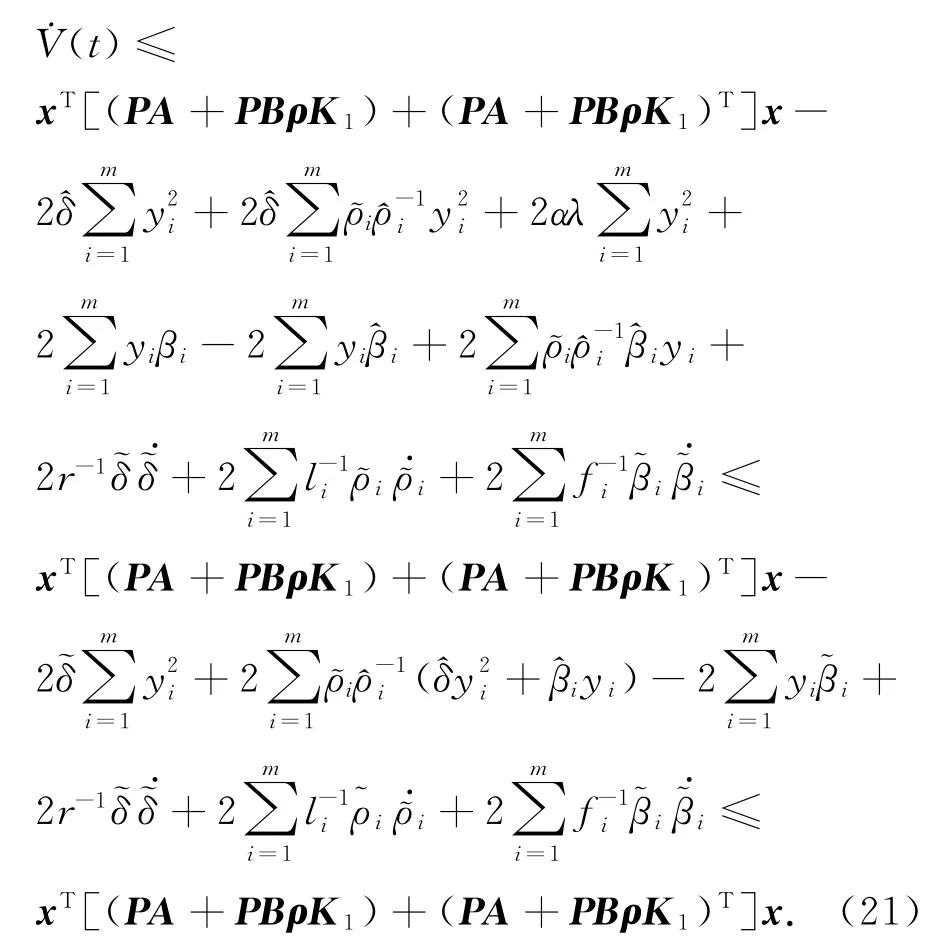
将式(21)分别左乘和右乘P-1,并令Q=P-1,W =K1Q,式(21)化为式(11).因此,若式(11)有解,则有˙V＜0.则对任意ρ∈Δρh,闭环系统稳定且所有信号有界.

注1:本文提出的自适应控制方法也需要估计执行器失效因子ρi,并应用估计值的倒数^ρ-1i(t)构造控制策略.只要选择权值li足够小,就可以保证^ρi(t)在初始值为^ρi(0)=1的情况下有限时间t1内不会趋向于0.可以调节其他自适应律权值fi,r,使得系统在有限时间t2＜t1内渐近稳定.

注2:本文提出的时变执行器偏移/卡死故障由状态依赖部分和常值卡死部分组成.显然如果系统达到渐近稳定状态,时变偏移/卡死故障转化为常值偏移/卡死故障.因此基于条件(6),本文提出的方法可以保证系统控制输入在系统状态趋于0时不会出现抖震现象.

3 仿真算例

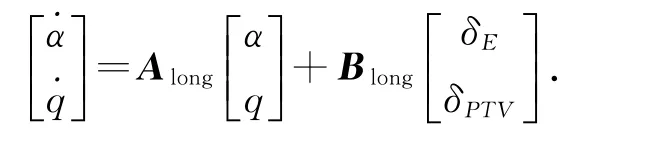
式中,

以及α=攻角,q=俯仰角速度,˙α=攻角变化率,˙q =俯仰角加速度,δE=升降舵位置,δPTV=俯仰推进速度.

考虑如下三种系统可能的模式:

正常模式1:所有两个执行器正常运行,即ρ11=ρ12=1.

故障模式2:第一个执行器可能正常运行,也可能发生偏移,第二个可能正常运行,也可能部分失效,描述为ρ21=1,0.1≤ρ22≤1.

故障模式3:第二个执行器可能正常运行,也可能发生偏移,第一个可能正常运行,也可能部分失效,描述为ρ32=1,0.1≤ρ31≤1.

为了证实所提出自适应方法的有效性,给出如下参数和初始值进行仿真:

r=1.5,li=0.2,fi=5,x(0)=[-4,5]T, ^δ(0)=5,^ρi(0)=1,^βi(0)=1,i=1,2.

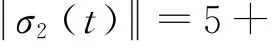
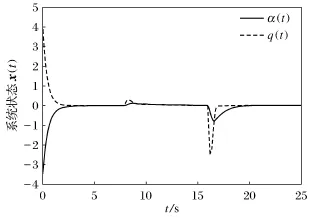
图1 系统状态响应曲线Fig.1 System status response curve

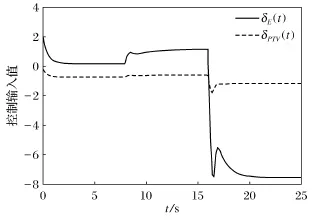
图2 系统输入响应曲线Fig.2 System input response curve

图1和图2分别描述了如上情形下系统的状态响应和控制输入曲线.图3～图5则分别是常值执行器失效因子ρi、偏移故障的状态依赖权重δ和偏移常量βi,i=1,2的估计响应曲线.从图中容易看出,本文所提出的自适应方法能够保证系统在执行器部分失效和偏移故障下的渐近稳定,且所有信号均收敛.

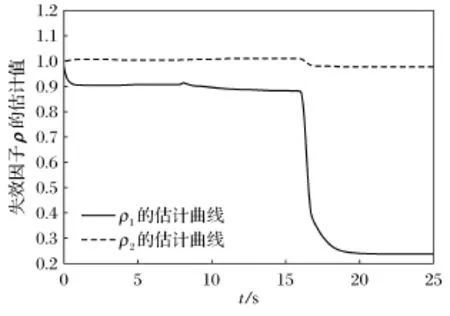
图3 执行器失效因子ρi,i=1,2估计曲线Fig.3 Estimation curve of actuator failurefactorρi,i=1,2

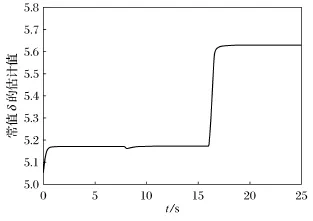
图4 偏移/卡死故障的状态依赖权重δ估计曲线Fig.4 Estimated curve of bias/stuck fault state-dependent weightsδ

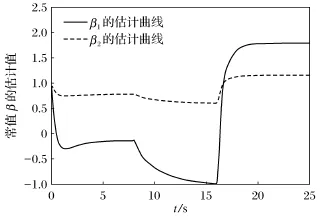
图5 偏移/卡死常量βi,i=1,2估计曲线Fig.5 Estimated curve of bias/stuck constantsβi,i=1,2

4 结 语

本文针对执行器部分失效和偏移的线性时不变系统,提出了一种自适应状态反馈控制策略,解决系统渐近稳定问题.所提出的自适应律在线调节了执行器失效因子、状态依赖权值和常值偏移故障,并且基于调节信息构造自适应控制器补偿故障所带来的影响.所得到的渐近稳定结果由李亚普诺夫方法得以证明.最后通过一个线性解耦的F18战斗机模型仿真显示了所提方法的有效性.

[1]Liao F,Wang J L,Yang G H.Reliable Robust Flight Tracking Control:An LMI Approach[J].IEEE Transactions on Control Systems Technology,2002,10 (1):7689.

[2]Veillette R J,Medanic J V,Perkins W R.Design of Reliable Control Systems[J].IEEE Transactions on Automatic Control,1992,37(3):290 304.

[3]Zhao Q,Jiang J.Reliable State Feedback Control System Design against Actuator Failures[J].Automatica,1998, 34(10):12671272.

[4]Wang H,Daley S.Actuator Fault Diagnosis:An Adaptive Observer-based Technique[J].IEEE Transactions on Automatic Control,1996,41(7):10731078.

[5]Jiang B,Chowdhury F N.Fault Estimation and Accommodation for Linear MIMO Discrete-time Systems [J].IEEE Transactions on Control Systems Technology,2005,13(3):493 499.

[6]Ye D,Yang G H.Adaptive Fault-tolerant Tracking Control against Actuator Faults with Application to Flight Control[J].IEEE Transactions on Control Systems Technology,2006,14(6):10881096.

[7]Tao G,Chen S H,Joshi S M.An Adaptive Control Scheme for Systems with Actuator Failures[J]. Automatica,2002,38(6):1027 1034.

[8]Tang X D,Tao G,Wang L F.Robust and Adaptive Actuator Failure Compensation Designs for a Rocket Fairing Structural-acoustic Model[J].IEEE Transactions on Aerospace and Electronic Systems,2004,40(4):13591366.

[9]Wang L F,Huang B,Tan K C.Fault-tolerant Vibration Control in a Networked and Embedded Rocket Fairing System[J].IEEE Transactions on Industrial Electronics, 2004,51(6):11271141.

[10]Jin X Z,Yang G H.Robust Adaptive Fault-tolerant Compensation Control with Actuator Failures and Bounded Disturbances[J].Acta Automatica Sinica, 2009,35(3):305309.

[11]Jin X Z,Yang G H,Li Y P.Robust Fault-tolerant Controller Design for Linear Time-invariant Systems with Actuator Failures:An Indirect Adaptive Method[J]. Control Theory&Applications,2010,8(4):391398.

[12]Jin X Z.Robust Adaptive Switching Fault-tolerant Control of a Class of Uncertain Systems Against Actuator Faults[J].Mathematical Problems in Engineering, 2014:11(Article ID 852502).

[13]Jin X Z,Yang G H,Chang X H.Robust H∞and Adaptive Tracking Control against Actuator Faults with a Linearised Aircraft Application[J].International Journal of Systems Sciences,2013,44(1):151165.

[14] 金小峥,杨光红,常晓恒,等.容错控制系统鲁棒H∞和自适应补偿设计[J].自动化学报,2013,39(1):3142. (Jin Xiaozheng,Yang Guanghong,Chang Xiaoheng,et al. Robust Fault-tolerant H∞Control with Adaptive Compensation[J].Acta Automatica Sinica,2013,39(1): 3142.)

[15]金小峥.一种自适应容错H∞控制方法研究[J].沈阳大学学报:自然科学版,2012,24(5):5558. (Jin Xiaozheng.Study on an Adaptive Fault-tolerant H∞Control Method[J].Journal of Shenyang University: Natural Science,2012,24(5):5558.)

[16]Jin X Z,Yang G H,Che W W.Adaptive Synchronization of Master-slave Large-scale Systems against Bias Actuators and Network Attenuations[J].International Journal of Control,Automation and Systems,2012,10 (6):11021110.

【责任编辑:王 颖】

Adaptive Fault-tolerant Control with a Class of Actuator Bias/Stuck Faults

Jin Xiaozheng
(Liaoning Provincial Key Laboratory of Manufacturing Industrial Integrated Automation,Shenyang University,Shenyang 110044,China)

An active fault-tolerant control problem of continuous-time linear invariant control systems with actuator faults is studied.The faults of losing of effectiveness and actuator-bias/stuck are considered,and the bias faults are assumed to be divided into two parts,that is,the time-varying state-dependence part and constant-bais/stuck part,where the dependency weight and constant values are unknown.Then,some adaptive laws are designed to estimate the unkown effency factors and dependency weight and constant values,and simultaneously,a state-feedback control function is constructed based on the estimations to compensate for the effects of actuator faults.Based on Lyapunove stability theory,it is proved that the proposed adaptive control strategy can guarantee the asymptotic stability of systems even in the cases of actuator faults.A numerical example is given to demonstrate the effectiveness of the proposed method.

fault-tolerant control;state feedback;actuator;bias/stuck faults;adaptive control

2095-5456(2014)01-0050-05

TP 13

A

20131105

国家自然科学基金资助项目(61104029);辽宁省高校杰出青年学者成长计划资助项目(LJQ2013122).

金小峥(1982),男,浙江金华人,沈阳大学副教授,博士.