变系数分数阶反应 扩散方程的数值解法

马亮亮,刘冬兵

(攀枝花学院数学与计算机学院,四川攀枝花 617000)

变系数分数阶反应 扩散方程的数值解法

马亮亮,刘冬兵

(攀枝花学院数学与计算机学院,四川攀枝花 617000)

考虑了变系数分数阶反应 扩散方程,将一阶的时间偏导数和二阶的空间偏导数分别用Caputo分数阶导数和Riemann-Liouville分数阶导数替换,利用L1算法和G算法对方程的变系数分数阶导数进行适当的离散,给出了该方程的一种计算有效的隐式差分格式,并证明了这个差分格式是无条件稳定和无条件收敛的,且具有o(τ+h)收敛阶.最后用数值例子说明差分格式是有效的.

变系数;反应 扩散方程;隐式差分;稳定性;收敛性

分数阶微分方程是经典的整数阶常微分方程的推广,它是将整数阶的导数用分数阶导数来替换.与整数阶微分方程相比,分数阶微分方程的优势在于它能更好地模拟自然界的物理过程和动态系统过程[1].当前,分数阶微分方程的研究正引起越来越多专家学者的关注,并已广泛应用于科学和工程的各个领域.

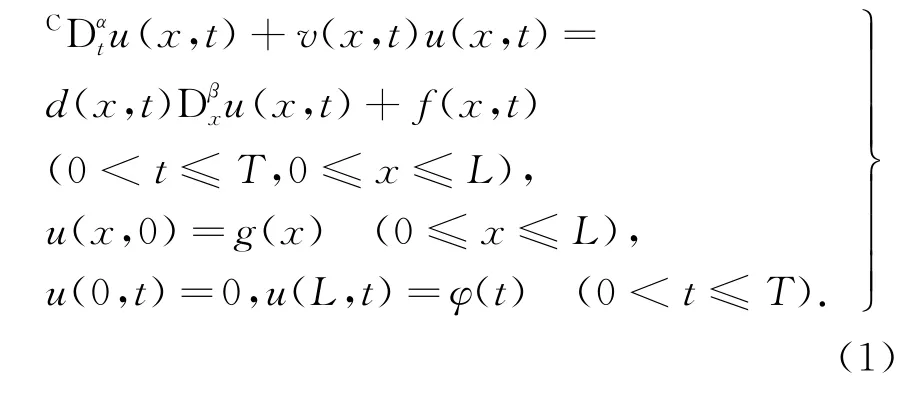
式中,0＜α≤1,1＜β≤2,且v(x,t)≥0,d(x,t)≥ 0u(x,t)是Caputo时间分数阶导数[9]:

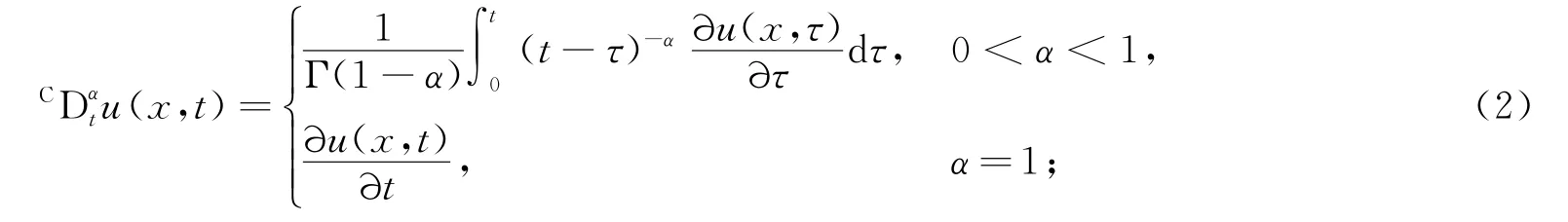
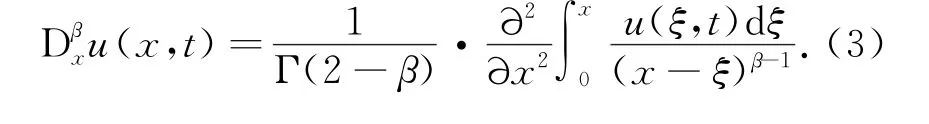
1 差分格式的建立

引理1(L1算法) 当0＜α≤1时,Caputo分数阶导数可以表示为

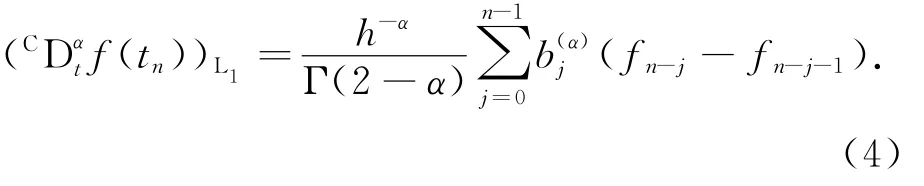
引理2(G算法) 分数阶微积分的差商逼近格式可以写成如下形式:

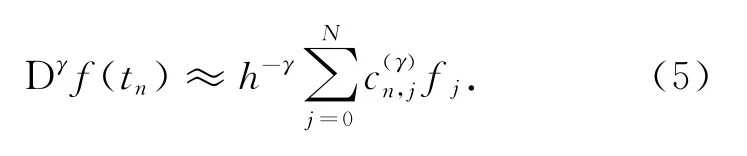
式中,系数c(γ)n,j依赖于n,j,γ,但与f无关,由各算 法确定,其中Gs(p)算法(p为正整数)如下:

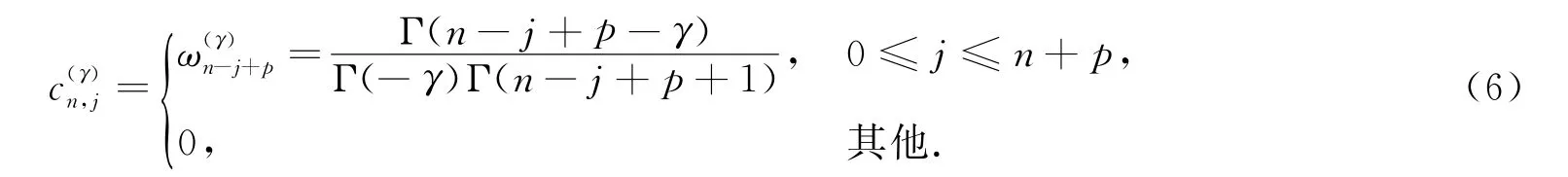
作网格剖分,令τ,h分别为时间步长和空间步长,设xi=ih(i=0,1,2,…,N;h=L/N),tk= kτ(k=0,1,2,…,M;τ=T/M).在方程(1)中, Caputo时间分数阶导数CDαtu(x,t)采用L1算法离散:

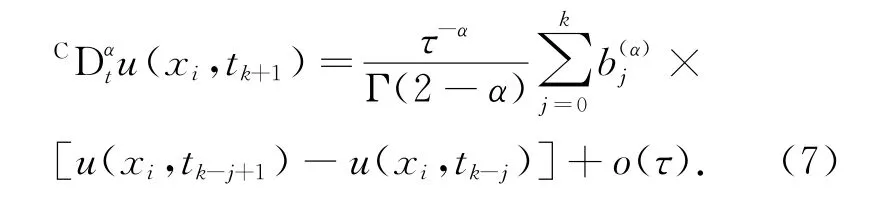
简记b(α)j=bj.

对于Riemann-Liouville空间分数阶导数,采用G算法替代.由于1＜β≤2,因此,Dβxu(x,t)的G算法中,最佳移位数是p=1,即采用Gs(1)算法离散:

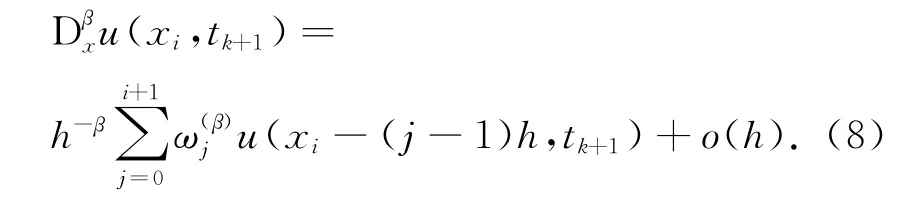
式中

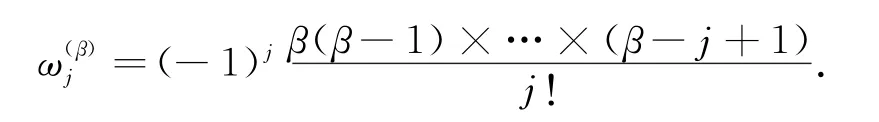
于是可得到如下隐式差分格式:

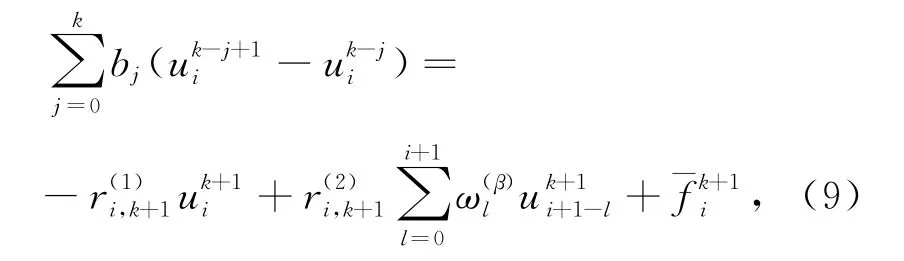
或改写为

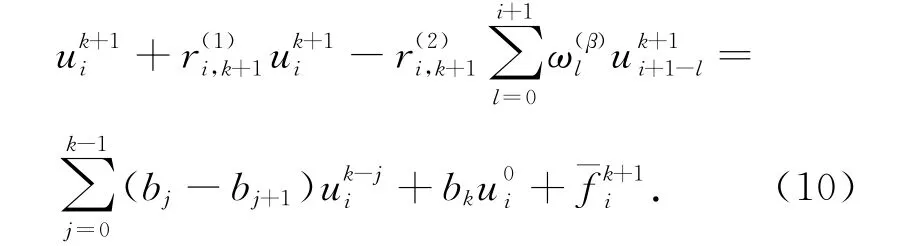
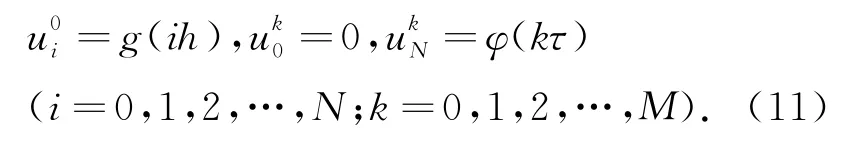
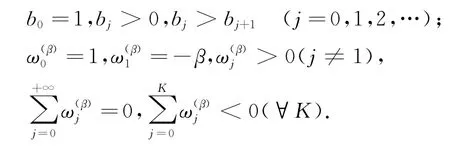
2 差分格式的分析

2.1 稳定性分析

记r(m)i,k=rm(m=1,2).定义两个差分算子L1和L2:

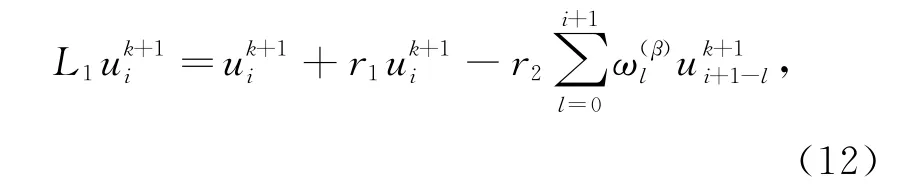
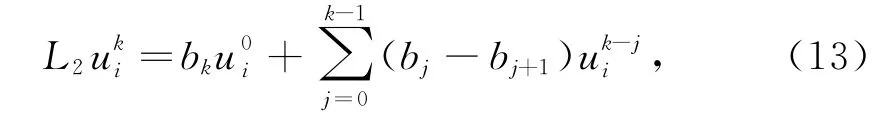
则隐式差分格式(10)可以写成

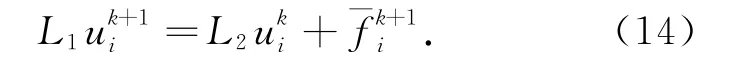
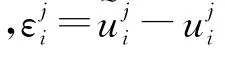
定理1 隐式差分格式(10)和格式(11)由初值引起的误差满足

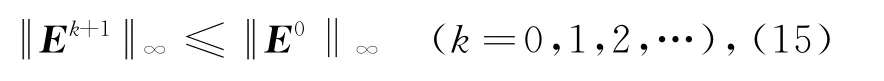
即差分格式无条件稳定.

证明 用数学归纳法证明.

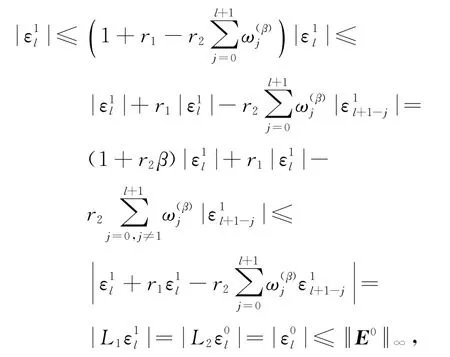
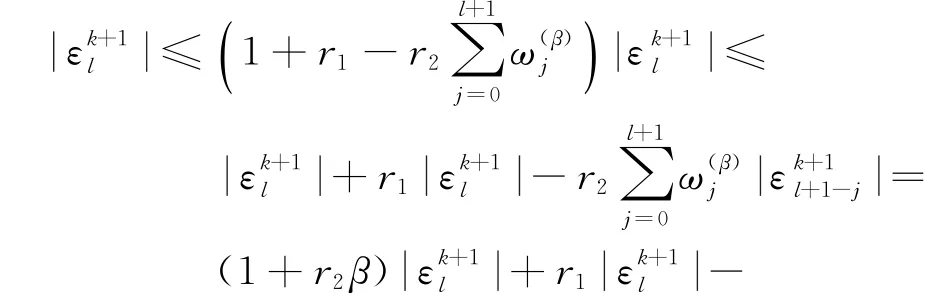
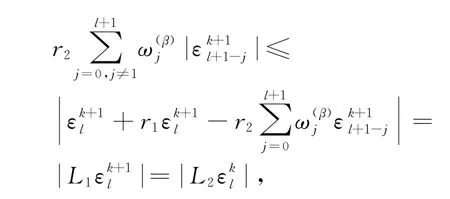
因此

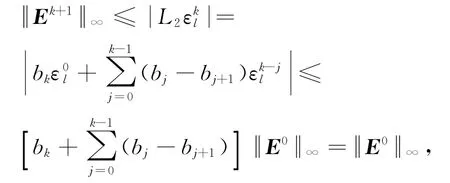
即隐式差分格式(10)和格式(11)关于初值无条件稳定.

2.2 收敛性分析

设u(xi,tk)(i=1,2,…,N-1;k=1,2,…, M)是方程(1)在网格节点上的精确解.定义该精确解与隐式差分格式(10)和格式(11)的数值解的误差为eki=u(xi,tk)-uki(i,k=1,2,…),并记ek=(ek

1,ek2,…,ek

N-1)T.显然e0=0,误差满足如下方程:

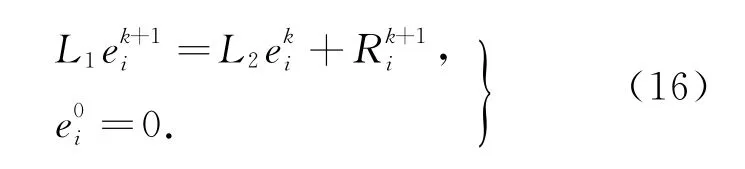
式中,Rik≤Cτα(τ+h);i=1,2,…,N-1;k=0, 1,2,…,M-1.

引理4 隐式差分格式(10)和格式(11)的数值解与精确解的误差满足

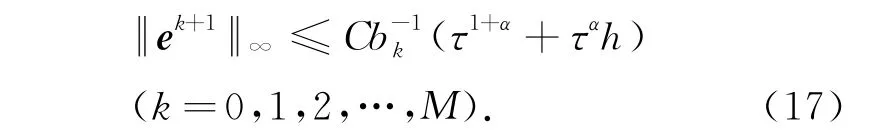
证明 采用数学归纳法证明.

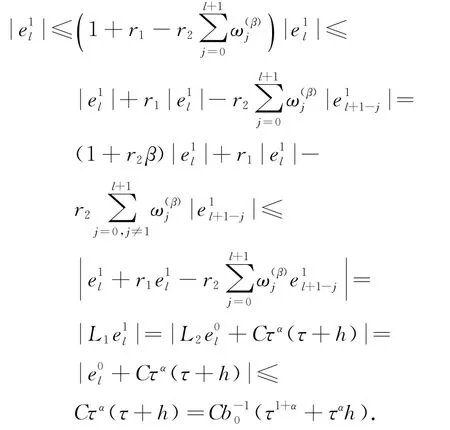
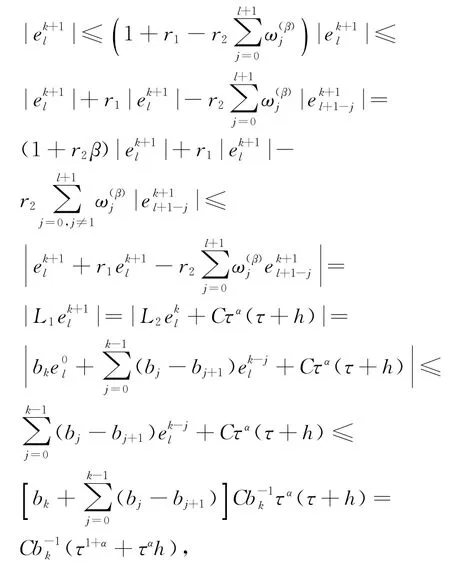
定理2 隐式差分格式(10)和格式(11)的数值解与精确解的误差满足

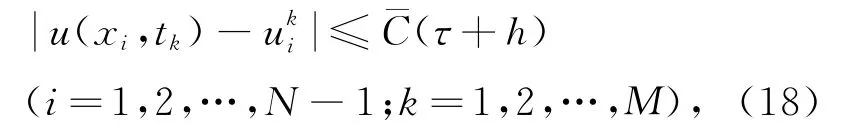
即差分格式收敛.

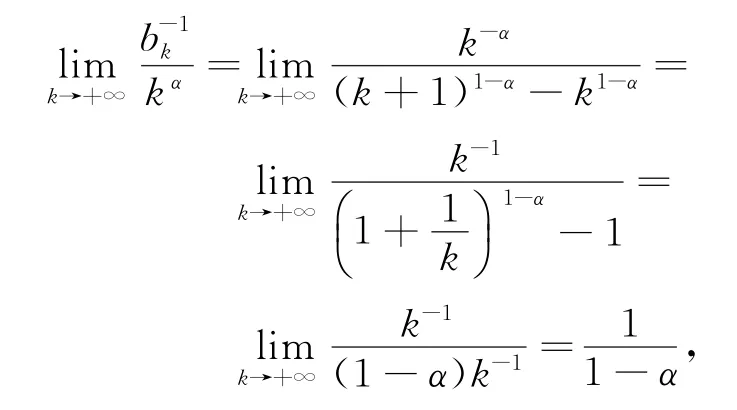
证明 因为所以,存在一个常数~C,使得bk-1≤C~kα.因为kτ≤T有限,所以,根据引理4有

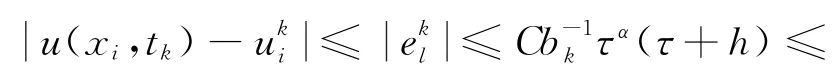
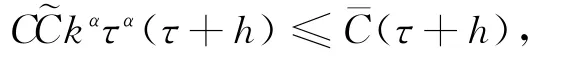
即差分格式收敛.

3 数值例子

考虑如下变系数分数阶反应-扩散方程:

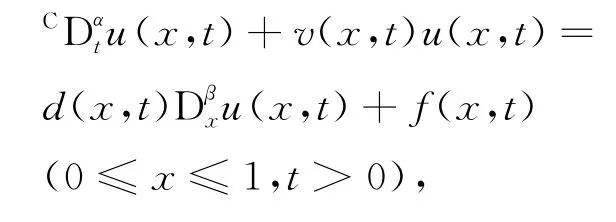
式中,

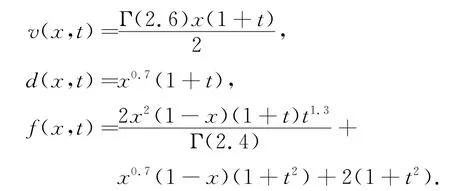
其边界条件为u(0,t)=u(1,t)=0(t＞0),初始条件为u(x,0)=g(x)=x2(1-x).此方程有精确解:u(x,t)=x2(1-x)(1+t)(1+t2).

取定时间步长τ=0.000 1,空间步长h= 0.02,α=0.7,β=1.3.图1是在t=0.01 s时刻由隐式差分格式(10)和格式(11)计算得到的数值解与精确解的平面图,可以看出,数值解收敛于精确解.图2是由隐式差分格式(10)和格式(11)计算得到的数值解与空间轴、时间轴之间的三维立体图.

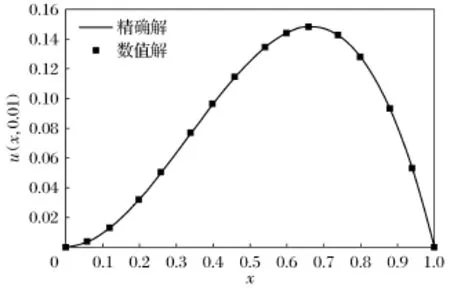
图1 数值解与精确解比较图Fig.1 Comparison on numerical solution and exact solution

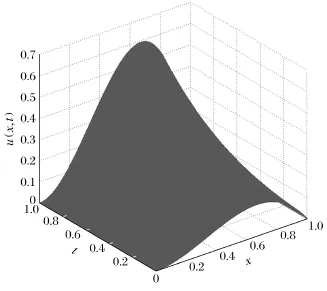
图2 三维立体图Fig.2 Stereoscopic graphic

4 结 语

本文考虑了一种与时间和空间都相关的变系数分数阶反应 扩散方程,利用L1算法和G算法对变系数分数阶导数进行离散,给出了一种计算有效的隐式差分格式,证明了此差分格式是无条件稳定的.然后利用分数阶离散系数的特点,证明了此差分格式也是无条件收敛的,且具有o(τ+h)收敛阶.

[1] 陈一鸣,仪明旭,魏金侠.小波方法求一类变系数分数阶微分方程数值解[J].西北师范大学学报:自然科学版, 2012,48(6):1721. (Chen Yiming,Yi Mingxu,Wei Jinxia.Wavelet Method to the Numerical Solution for a Class of Fractional Differential Equation with Variable Coefficient[J]. Journal of Northwest Normal University:Natural Science,2012,48(6):1721.)

[2]Wyss W.The Fractional Diffusion Equation[J].Journal of Mathematical Physics,1986,27(11):27822785.

[3]Mainardi F,Luchko Y,Pagnini G.The Fundamental Solution of the Space-time Fractional Diffusion Equation [J].Fractional Calculus and Applied Analysis,2001,4 (2):153192.

[4]Gorenflo R,Mainardi F,Moretti D,et al.Discrete Random Walk Models for Space-time Fractional Diffusion[J]. Chemical Physics,2002,284(1/2):521541.

[5]庄平辉,刘发旺.空间 时间分数阶扩散方程的显式差分近似[J].高等学校计算数学学报,2005,27(12):223228. (Zhuang Pinghui,Liu Fawang.An Explicit Approximation for the Space-time Fractional Diffusion Equation[J].Numerical Mathematics A Journal of Chinese Universities,2005,27(12):223228.)

[6]Gorenflo R,Mainardi F.Random Walk Models for Spacefractional Diffusion Processes[J].Fractional Calculus& Applied Analysis,1998,1(2):167191.

[7]覃平阳,张晓丹.空间 时间分数阶对流扩散方程的数值解法[J].计算数学,2008,30(3):305310. (Qin Pingyang,Zhang Xiaodan.An Numerical Method for the Space-time Fractional Convection-Diffusion Equation [J].Mathematics Numerica Sinica,2008,30(3):305310.)

[8]陈景华.Caputo分数阶反应 扩散方程的隐式差分逼近[J].厦门大学学报:自然科学版,2007,46(5):616 619. (Chen Jinghua.An Implicit Approximation for the Caputo Fractional Reaction-Dispersion Equation[J].Journal of Xiamen University:Natural Science,2007,46(5):616619.)

[9]Podlubny I.Fractional Differential Equations[M].San Diego:Academic Press,1999.

[10] 郭柏灵,蒲学科,黄凤辉.分数阶偏微分方程及其数值解[M].北京:科学出版社,2011. (Guo Bailing,Pu Xueke,Huang Fenghui.Fractional Partial Differential Equations and their Numerical Solutions[M].Beijing:Science Press,2011.)

【责任编辑:王 颖】

A Numerical Method for Fractional Reaction-Dispersion Equation with Variable Coefficients

Ma Liangliang,Liu Dongbing
(College of Mathematics and Computer,Panzhihua University,Panzhihua 617000,China)

A fractional reaction-dispersion equation with variable coefficients is considered which the first-order time derivative and the second-order space derivative is replacing by Caputo fractional derivative and Riemann-Liouville derivative respectively,and an implicit difference scheme is presented by using the algorithm of L1and G to discrete the variable coefficients fractional derivative efficaciously.It is showed that the scheme is unconditional stable and convergence respectively,the convergence order of the scheme is o(τ+h).Finally,a numerical example demonstrates the difference method is effective.

variable coefficients;reaction-dispersion equation;implicit difference;stability; convergence

2095-5456(2014)01-0076-05

O 241.82

A

2013 03 30

国家自然科学基金资助项目(10671132,60673192);攀枝花学院校级科研项目(2013YB05).

马亮亮(1986),男,甘肃天水人,攀枝花学院讲师.