一类高阶泛函微分方程解的振动性

曾海璇

（韩山师范学院数学与统计学系，广东潮州 521041）

1 引言和引理

1987年，G.S.ladas等人系统地提出并证明可以利用特征方程没有实根来建立常参数微分方程的振动准则．2012年，Hasan Öğünmez利用特征方程没有实根来建立方程的振动准则，研究并得到系数为矩阵的奇数阶泛函微分方程的振动准则[1]．本文以特征方程特征根存在与否作为判断方程振动性的依据，研究以下中立型泛函微分方程：

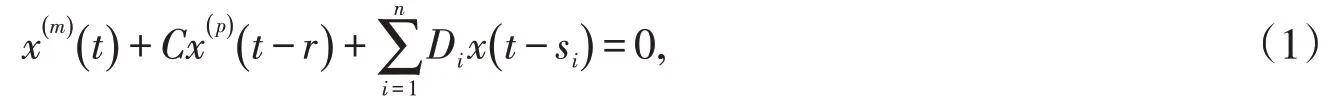
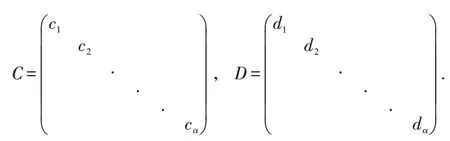
给出其振动的充分条件、必要条件等判定定理．其中C，Di∈Rα×α，r ＞0，si＞0(i=1,2,...,n)对应的特征方程为

定义1 设x(t)是某一泛函微分方程的解，如果x(t)不是最终零解，且存在一序列{ti} ，使得x(ti)=0，则称x(t)是此方程的一个振动解，或称x(t)是振动的，否则，则称x(t)是此方程的非振动解，或称解x(t)是非振动的．

定义2 设P ∈Rα×α， μ(P)为P 的对数范数，取，其中(Pξ,ξ)是Rα空间中的内积，且

引理1 若si＞r ＞0,C,Di∈Rα×α，方程（1）的所有解振动当且仅当对应的特征方程（2）没有实根．

引理2 假设方程（1）中，m=p=n=1，C 和D1为对角阵，则方程（1）所有解振动的必要条件是s1＞r，且C 正定．

引 理3 若 在 方 程（1） 中， m=p=n=1 ， C=I （ I 为 单 位 矩 阵）， s1＞r ， D1在上没有特征根，则方程（1）振动．

证明 若m=p=n=1，C=I，方程（1）对应的特征方程为：

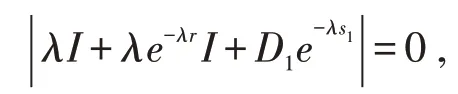
即

由引理1可知，当D1在上没有特征根时，方程（1）的所有解振动．

引理4 若在方程（1）中，m=p=1，C=I （I 为单位矩阵），si＞r(i=1,2,...,n)，满足

则方程（1）的所有解振动．

证明 利用反证法，假设方程（1）存在非振动解，则对应的特征方程（2）存在实根λ0，即存在向量u ∈Rα且‖ ‖u =1，使得

则有

当λ0＞0 时，当λ0＜0 时,

引理5 若在方程（1）中，m=p=n=1，s1＞r，C+D1=0．方程（1）的所有解振动，则矩阵D1在(]-∞,0 上没有特征根．

证明 由C+D1=0 可知，特征方程

令z=min{v (λ)|0 ＜λ ＜λ0} ，知z ＜0，则v(λ) 的值域为[ z,+∞)，根据引理1即当且仅当C 在(- ∞,z]上没有特征根时，方程（1）的所有解振动．又(- ∞,0]⊂(-∞,z]，则方程（1）的所有解振动可知C在(- ∞,0]上没有特征根．

2 主要结果

定理1 若在方程（1）中，m=p=1，C=I （I 为单位矩阵），si＞r，μ(-Di)≤0(i =1,2,...,n)，若满足下列其中一个条件，方程（1）的所有解振动：

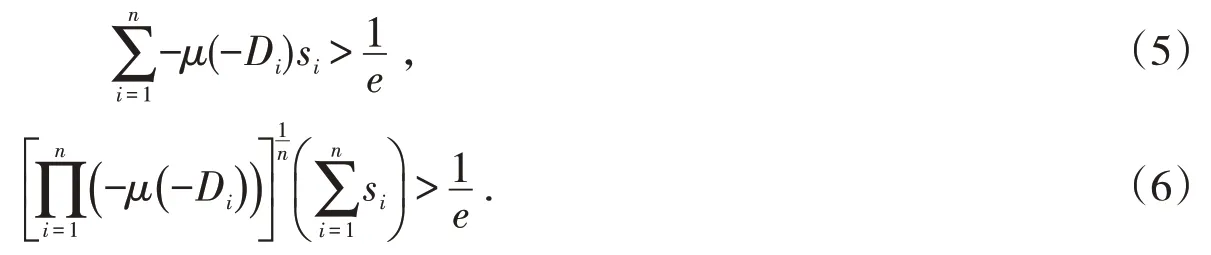
证明 利用引理4，由μ(-Di)≤0，知（3）成立，下证（4）成立．若（5）成立，当λ ＜0 时，

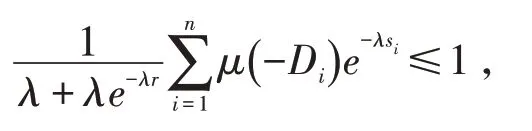
即

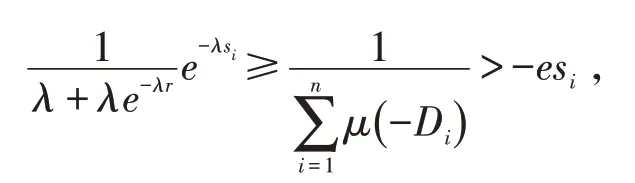
则有

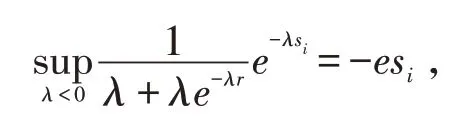
所以

得

即有

结合式（6），则可证（4）式成立．

推论1 若在方程（1）中，m ＞p ≥1，si＞r(i=1,2,...,n)，C=I （I 为单位矩阵），且m,p 为奇数，满足则方程（1）振动．

证明 与引理4证明方法类似．

推论2 若在方程（1）中，m ＞p ≥1，si＞r(i =1,2,...,n)，C=I （I 为单位矩阵），且m,p 为奇数，满足下列其中一个条件

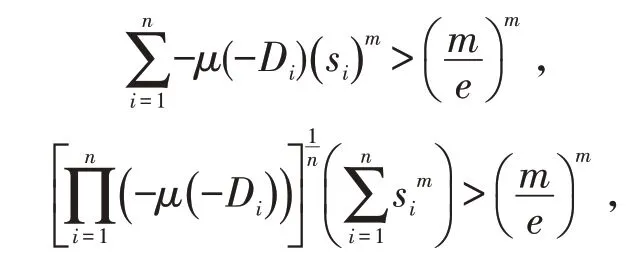
则方程（1）振动．

证明 与定理1证明方法类似．

推论3 若在方程（1）中，n=1，m ＞p ≥1，s1＞r，m 和p 为奇数且C+D1=0．方程（1）的所有解振动，则矩阵C 在(]-∞,0 上没有特征根．

证明 与引理5的证明方法类似．

定理2 假设在方程（1）中，m=p=n=1， s1＞r ，C 和D1为对角阵且C 正定．若存在满足(l+h)r ＞e-1+kr的常数k ＞0，l ＞0，l+h ＞0，且

其中

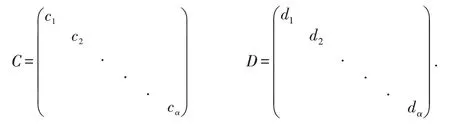
则方程（1）的一切解振动．

证明 在方程（1）中，m=p=n=1，s1＞r，C 和D1为对角阵

因为C 正定，所以ci∈R+．

引入常参数k ＞0，l ＞0，l+h ＞0 及待定参数a ＞0,b ＞0 （a+b=1），方程（1）对应的特征方程为

由（7）、（8）及（9）式可得

若对∀λ ∈R，ωi()λ ＞0，则方程（1）振动．

要使ωi()λ ＞0，则只要成立

所以（11）式和（12）式等价于

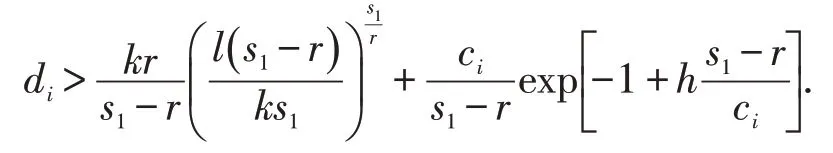
限制C，s1，r，可得到

定理3 若在方程（1）中，m=p=n=1，s1＞r，C 和D1为对角阵．

（1）当C 正定，且r ＜s1＜2r 时，方程（1）的一切解振动的充要条件为

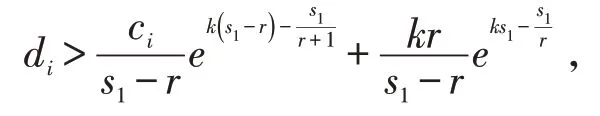
（2）当C 负定，r ＞s1时方程（1）的一切解振动的充要条件为

定理4 若在方程（1）中，m=p ＞1，n=1，s1＞r，CD1=I 且C 和D1为对角阵，m 为奇数．则方程必存在非振动解．

其中

证明 m=p ＞1，n=1，则方程（1）对应的特征方程为

因为CD=I ，可知cidi=1，即ci≠0，di≠0．所以的零解即为vi()λ的零解．

又因为e-λs1＞0,即g(di)有最小值，又因为对称轴为

综上所述，存在λ0，使得h(λ0)=0，即方程（1）必存在非振动的解．

3 附注

附注1 若方程（1）中C=0，n=1，s1＞0，m 为正奇数，则由本文引理3和引理5，即得到文献[1]的定理2.1．

附注2 若方程（1）中C=0，si＞0(i=1,2,...,n)，m 为正奇数，则由本文引理4和定理1，即得到文献[1]的引理3.1和定理3.2．

附注3 若方程（1）中m=p=n=1，s1＞r，α=1，则由本文定理2，即得到文献[2]第九章的引理2.2，定理2.1和定理2.2．

[1]Hasan Öğünmez, Özkan Öcaln.Oscillation of Higher Order Systems of Differential Equations[J].Journal of Math Analysis，2013，15：735-740．

[2]郑祖庥．泛函微分方程理论[M]．合肥：安徽教育出版社，1994：331-356．

[3]李森林，温立志．泛函微分方程[M]．长沙：湖南科学技术出版社，1987：380-416.