关于一个特殊的自相似集的Hausdorff测度的准确值的计算

洪若诗，黄小燕

（韩山师范学院数学与统计学系，广东潮州 521041）

1 引言与预备知识

众所周知，Hausdorff 测度理论是分形几何的理论基础，因此如何计算或估计分形集的Hausdorff测度是个十分重要的问题．近年来，许多作者都致力于一类自相似集的Hausdorff 测度的准确值的研究，得到了很多有价值的成果，见文献[1-10]．文献[1]研究了由如下5个相似压缩

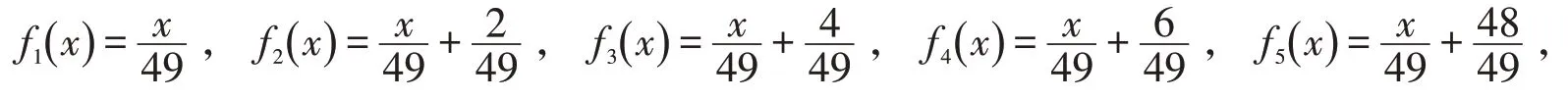
确定的自相似集，得到了该自相似集的Hausdorff测度的准确值，即

命题A 设E 是由上述迭代函数系{ f1，f2，f3，f4，f5} 确定的自相似集，记则

为证明命题A，文献[1]利用了如下引理．

事实上，引理A中的不等式（1）不成立，因而命题A的结论不可靠．本文旨在进一步研究这些问题．首先建立一些新的不等式，然后在此基础上利用文献[10]给出的一个基本结论，计算出上述自相似集的Hausdorff测度的准确值．

下面给出计算自相似集的Hausdorff测度准确值的一个基本结论．

引理1[10]设E ⊂Rn是由相似压缩{ }S1,∙∙∙,Sm所确定的满足开集条件的自相似集，dimHE=s，且压缩比相等(c1=c2=∙∙∙=cm=c)，则.若存在正整数k0与N0()以及某k0级拷贝串（即N0个ck0-E 之并），使得，对任意k ≥0，N()1 ≤N ≤mk，以及任意表示的任意N个级拷贝串之并），则

2 主要结果

为了得到命题A所讨论的自相似集的Hausdorff测度的准确值，首先给出两个有用的引理.

证明 令

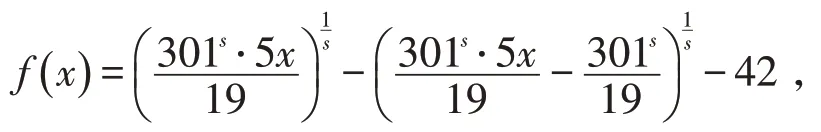
则

又

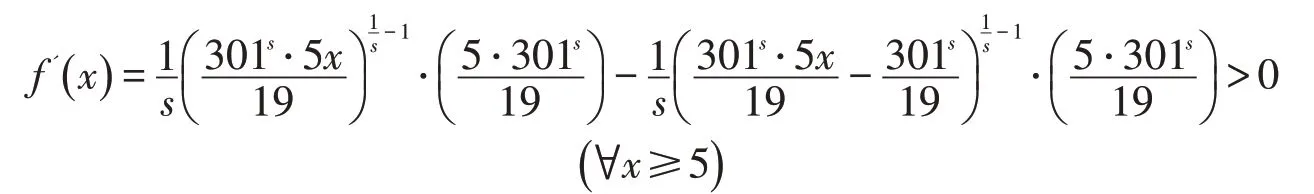
故

成立.

引理3 设n ≥3，s=log75，则以下不等式成立：

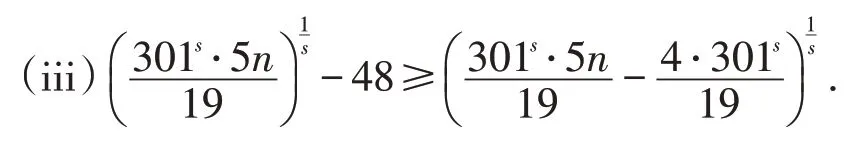
证明 令

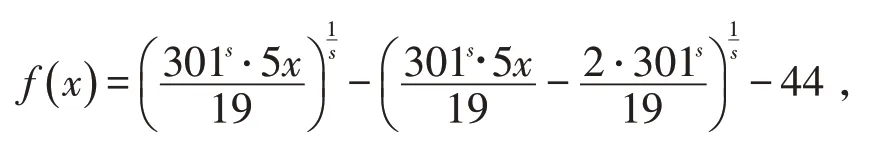
则

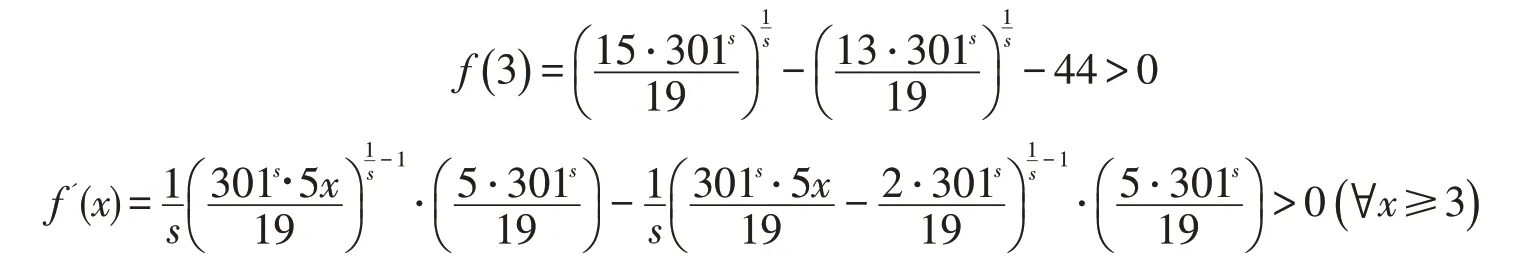
故（i）成立.

（i）与（iii）的证明方法同（1），从略.

定理1 设E 是命题A中迭代函数系{ f1，f2，f3，f4，f5} 所确定的自相似集，则

证明 下面验证自相似集E 满足引理1的条件.

首先，取k0=2，N0=19，于是

下证，对任意k 及N(1 ≤N ≤5k)有

当k=1时，

若N=1，则

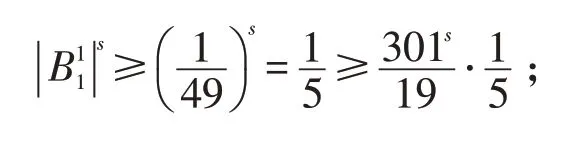
若N=2，则

若N=3，则

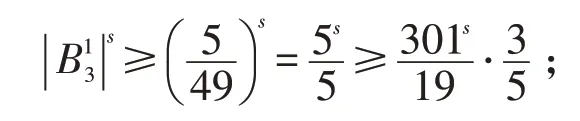
若N=4，则

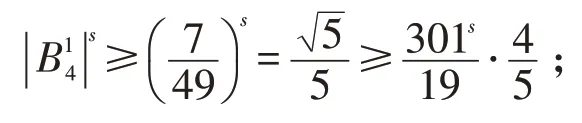
若N=5，则

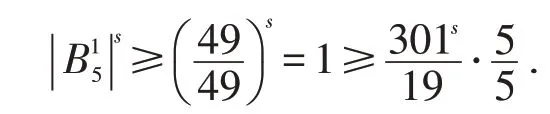
所以，当k=1时，（1）式成立.

假设对于正整数k 以及任意正整数N(1 ≤N ≤5k)，（1）式成立，则对于正整数k+1：

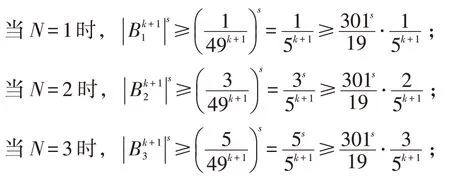
当N=5n-1时，

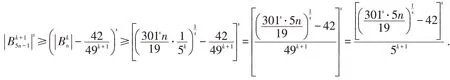
由引理2可得

当N=5n-2 时，

当N=5n-3 时，

由引理3（ii）可得

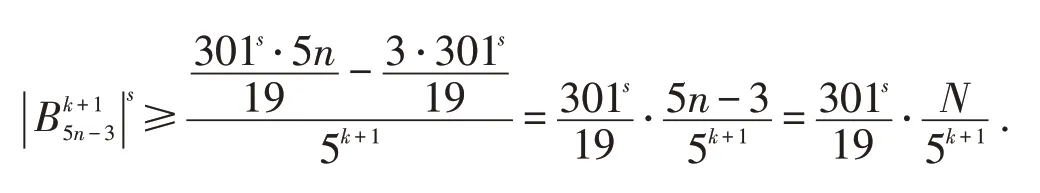
当N=5n-4 时，

由引理3（iii）可得

因此，对任意正整数N(1 ≤N ≤5k)，有成立.

[1]殷峰丽．一个特殊的自相似集的Hausdorff测度[J]．周口师范学院学报，2014，31（2）：14-17.

[2]ZHOU Z, FENG L.TwelveOpenProblemsontheExactValueoftheHausdorffMeasureandonTopological Entropy: a Brief Survey of Recent Results[J].Nonlinearity,2004(17):493-502.

[3]MARION J.Mesures de Hausdorff D’ensembles Fractals[J].Ann.Sci.Math.Quebec,1987(11):111-132.

[4]SRICHARTS R S.Exact Hausdorff Measure and Intervals of Maximum Density for Cantor Sets[J].Trans.Amer.Math.Soc.,1999,351:3725-3741.

[5]WU M.The Hausdorff Measure of Some Sierpinski Carpets[J].Chaos,Solitons and Fractals,2005,24:717-731.

[6]ZHOU Z.Hausdorff Measure of Self-Similar Set-the Koch Curve[J].Sci.China.Ser.,A:1998,41:723-728.

[7]ZHOU Z,FENG L.A New Estimate of the Hausdorff Measure of the Sierpinski Gasket[J].Nonlinearity, 2000(13):479-491.

[8]ZHOU Z,WU M.The Hausdorff Measure of a Sierpinski Carpet[J].Sci.China,A1999,47:673-680.

[9]ZHOU Z,WU M,ZHAO Y.The Hausdorff Measure of a Class of Ggeneralized Sierpinski Sponges[J].Chin.J.Contemp.Math.,2001,22:55-64.

[10]许绍元，周作领，苏维宜．自相似集的质量分布原理与Hausdorff测度及其应用[J]．数学学报：中文版，2010，53（1）：117-124.