含多个p-Laplacian算子Duffing型方程周期解的存在唯一性
2014-10-30陈仕洲
陈仕洲
(韩山师范学院数学与统计学系,广东潮州 521041)
1 引言及引理
p-Laplacian 方程作为一物理模型,在非牛顿流体力学、非线性弹性理论和工程技术等许多重要领域中有广泛的应用[1-6].在这些应用中,重要的是要知道p-Laplacian 方程周期解的存在性.文献[2]、文献[3]分别研究了一类具偏差变元的二阶p-Laplacian方程
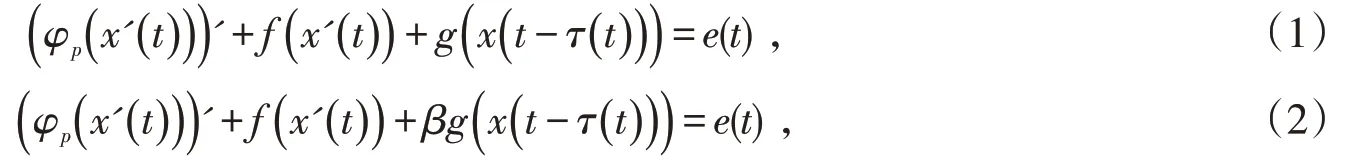
周期解的存在问题.文献[4]、文献[5]分别研究了

周期解的存在性和唯一性()p ≥2 .文献[6]研究了
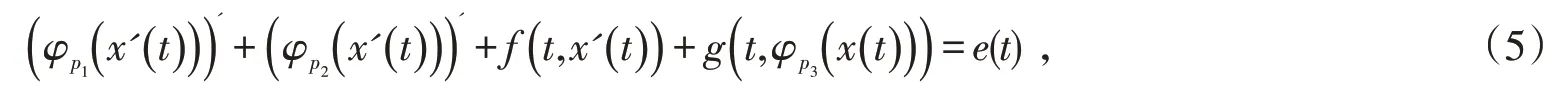
周期解的存在性,其中pi>1()i=1,2,3 ,p1>p2,p3<2.本文将利用重合度Mawhin连续定理,研究
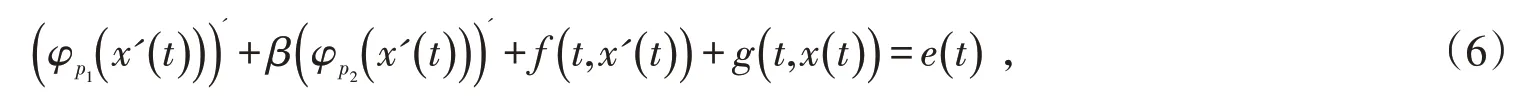
且当β=0 时实质上推广和改进了文献[5]的结果.
为证明本文的主要结果,需要以下引理.
引理1[1]设为有界开集,是Caratheodory函数.如果
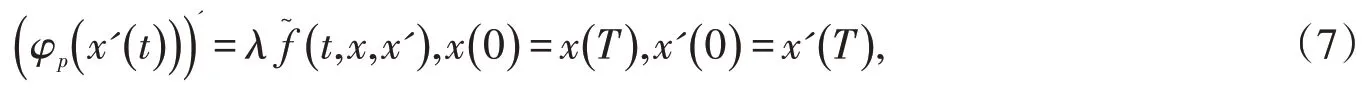
在∂Ω 上无解.
(ii)方程
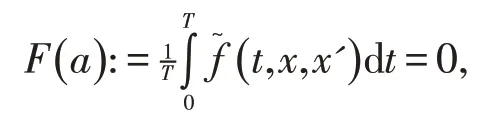
在∂Ω ⋂R 上无解.
(iii)Brouwer度deg{F,Ω ⋂R,0}≠0.
2 主要结果
定理1 设
(H3) p1>α;或p1=α,d ⋅r <1.则方程(6)存在一个T-周期解.
证明 考虑方程(6)的同伦方程
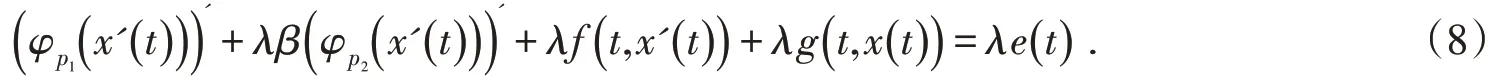
设x ∈C1T是方程(8)的任一解,t1,t2∈分别是x(t)在[0 ,T]上的最大值点和最小值点,则x'(ti)=0,i=1,2,则可以断言:
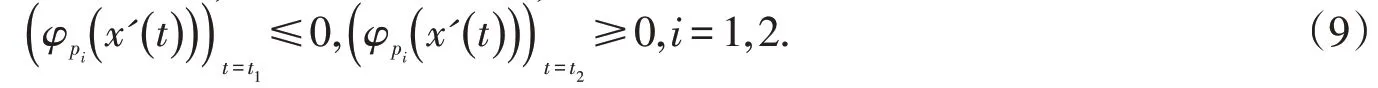
由方程(8)得

由(10)和(H2)即得

由(11)即得 ||x∞≤d.
方程(8)两边同乘以x()t ,并应用(H1)和(12)得


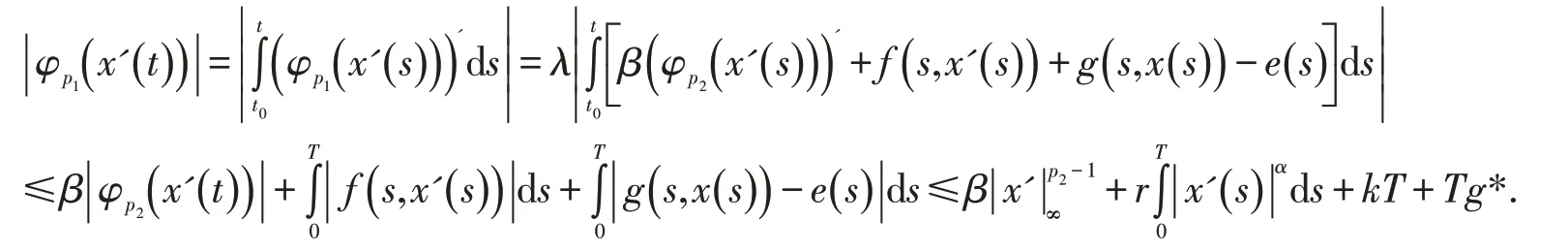
并注意到(14),可得
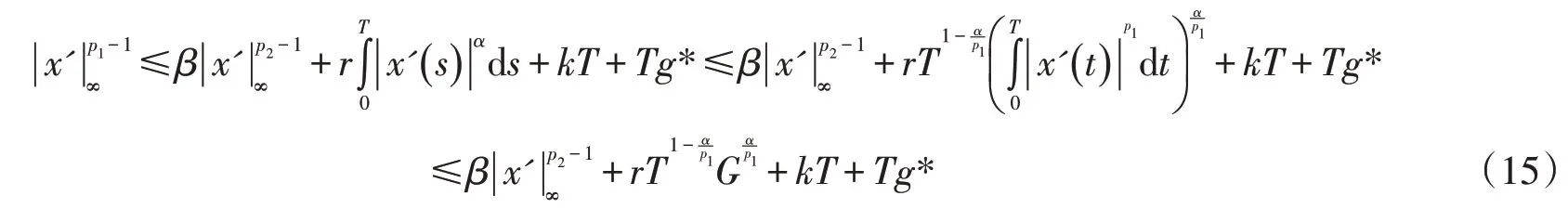

因此引理1的条件(ii)被满足.作变换
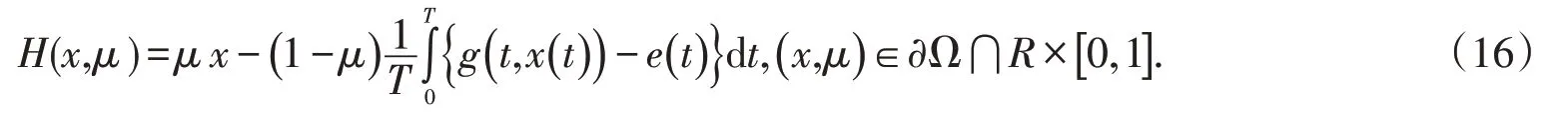
由(H2)有
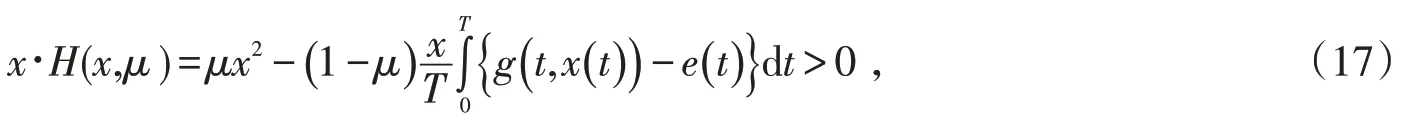
故H(x,μ)为同伦变换且
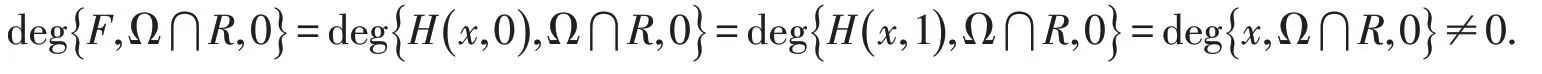
因此引理1的条件(iii)也被满足.由引理1,方程(6)有一个T-周期解x(t).
定理2 设
(H4)
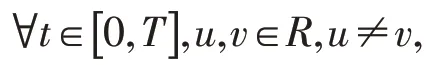

则方程(6)至多存在一个T-周期解.
证 设x1(t),x2(t)为方程(6)的两个T周期解,则


由(19)、(20)和(H3),得
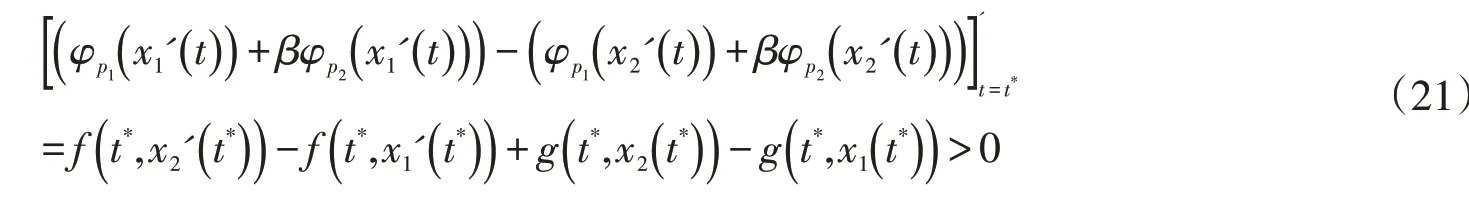
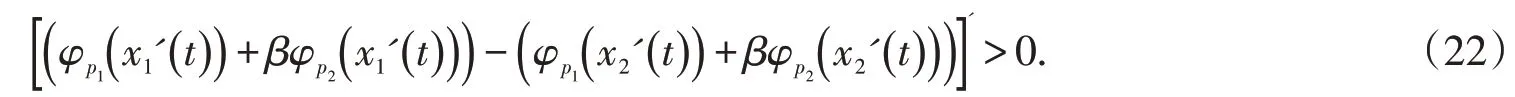
注意到

即得
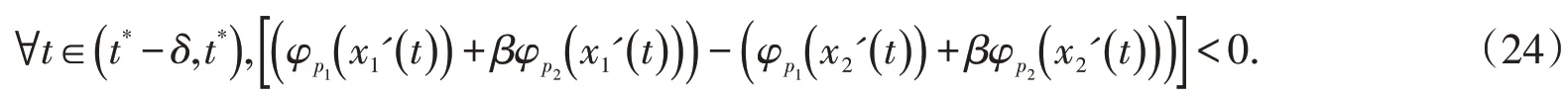
由于函数φp1(v)+βφp2(v)是严格递增的,故

即方程(6)至多有一个T-周期解.
由定理1-2立即得到.
定理3 设(H1) 、(H2)、(H3) 、(H4)都被满足,则方程(6)有且仅有一个T- 周期解.
3 注记和例子
注记1 将定理2、定理3中条件()H4 替换为
(H4)*∀t ∈[0 ,T],u,v ∈R,u ≠v,(g(t,u)-g(t,v))(u -v)>0
其余条件不变,定理2、定理3结论仍然成立.
注记2 令β=0,f()t,u =cu,则由定理3即得文献[4]的主要结果.
注记3 令β=0,则容易看出定理3推广和改进文献[5]的主要结果.
例 考虑方程

容易验证定理3的条件都被满足,故方程(26)有唯一2π 周期解.
[1]MANáSEVICH R, MAWHIN J.Periodic solutions for nonlinear systems with p-Laplacian-like operator [J].J.Differ.Equ,1998,145:367-393.
[2]鲁世平,葛渭高.具偏差变元的二阶Laplacian方程周期解存在性问题[J].数学学报,2005,48(5):841-850.
[3]CHEUNG W S, REN J.On the existence of periodic solutions for p-Laplacian generalized Liénard equation[J].Nonlinear Analysis:Theory,Methods&Applications,2005,60(1):65-75.
[4]HE Zhan-bing,WANG Wen-tao,YI Xue-jun.Existence and uniqueness of periodic solutions for Rayleigh type Laplacian equation[J].Journal of Computational and Applied Mathematics,2009,232(2):558-564.
[5]YANG X,KIM Y I,LO K.Periodic solutions for a generalized p-Laplacian equation[J].Applied Mathematics Letters,2012,25:586-589.
[6]ZHOU Zong-fu,ZENG Li,JIA Bao-rui,et al.Periodic Solutions to Duffing Type p-Laplacian equation with several p-Laplacian operations[J].Ann.of Diff.Eqs,2013,29(1):121-126.
