锥度量空间中两类混合单调算子的公共不动点定理

李承耕，刘 波

（韩山师范学院数学与统计学系，广东潮州 521041）

混合单调算子是一类非常重要的算子，1987年由郭大钧教授和V.Lakshmikantham 提出．很多学者对此做了大量的研究，得到了一批很好的结果[1-7]，它的很多理论被应用于非线性微分方程和非线性积分方程解的存在性问题的研究．本文在文献[8]的基础上，并结合文献[9]的基本计算技巧讨论了两类混合单调算子的公共不动点问题，并给出了迭代序列收敛于解的误差估计，推广了已有文献的一些结论．

1 预备知识

设E 是一个实Banach空间，如果P 是E 中的非空凸闭集，且满足以下条件：

（1） x ∈P，λ ≥0 ⇒λx ∈P；

（2） x ∈P，-x ∈P ⇒x=θ，θ 是P 中零元；则称P 为E 中的一个锥．

设半序“≤”是E 中的锥P 产生的，即∀x,y ∈E，若y-x ∈P，则x ≤y.如果x ≤y，且x ≠y，则记x ＜y.

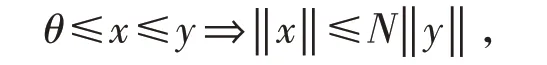
定义1[3]设P 是E 中一个锥，如果存在常数N ＞0，使得则称P 是正规锥，满足上式的正数N 中最小者叫做P 的正规常数．

显然，正规常数N ≥1．

定义2[3]设D ⊂E，算子A:D×D →E，

（1）如果x1,x2,y1,y2∈D，x1≤x2,y1≥y2蕴含着A(x1,y1)≤A()x2,y2，则称A 是混合单调算子；如果A 与第一变元无关，则称A是减算子；

（2）如果(x*,y*) ∈D×D 满足x*=A(x*,y*) ，y*=A(y*,x*) ，则称(x*,y*) 是A 的耦合不动点；

2 主要结果

定理1 设E 是完备的锥度量空间，且A,B:[u0,v0]×[u0,v0]→E，是两个混合单调算子，且满足下列条件：

(i) 存在常数β ∈(0,1) ，使得A(v,u)-A(u,v)≤2β(v-u)，u0≤u ≤v ≤v0；

(ii)A(v,u)-B(u,v)≥-2α(v-u)，当u ≤v；

则算子方程组

在[u]0,v0中有唯一的公共解u*．而且迭代序列

n=0,1,2,.......，都收敛于u*，并且有误差估计

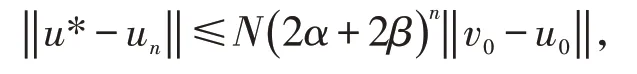
其中N 为P 的正规常数．

证明 构造迭代序列为

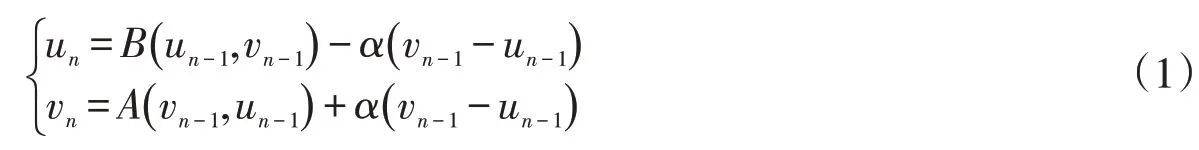
其中n=0,1,2,........由数学归纳法，当n=1时，由条件()iii 和A，B为混合单调算子，有

由迭代式（1）和条件(ii)

即u0≤u1≤v1≤v0成立.

假设n=k 时，有

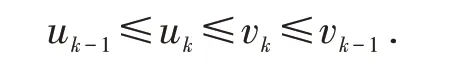
当n=k+1时，由A,B为单调混合算子可得

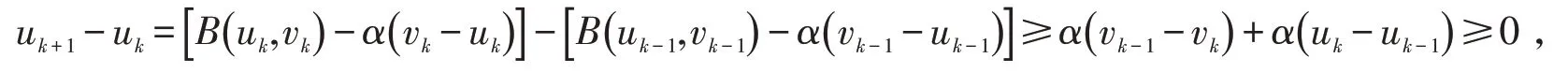
同理有，

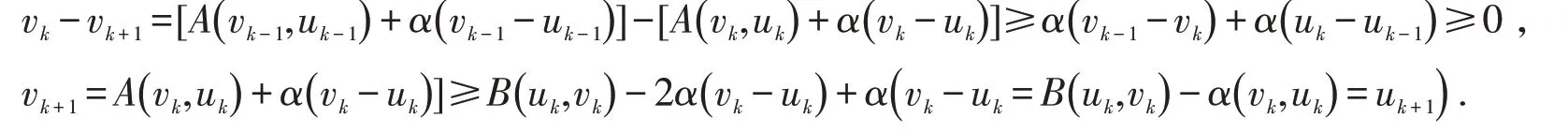
得到

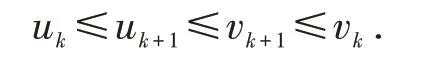
综上可得

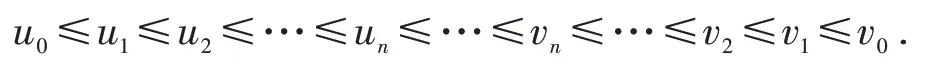
下证{un} ,{vn} 是Cauchy列．由条件（i）有

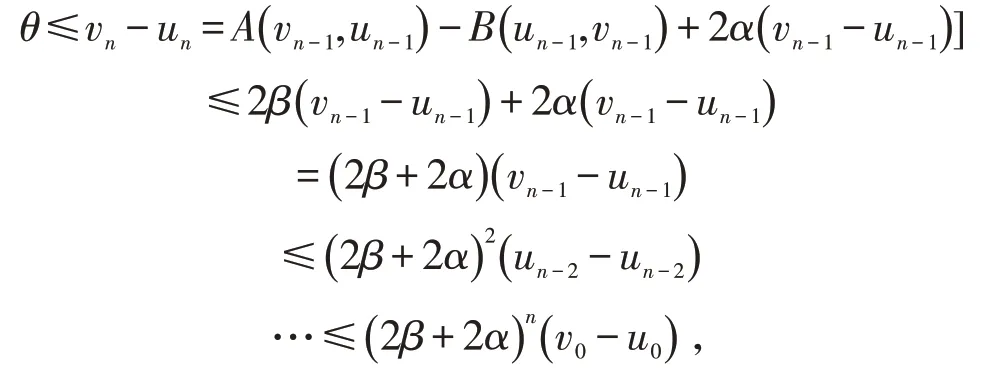
于是，对于任意的自然数m,n 有，

于是，由P 的正规性，有

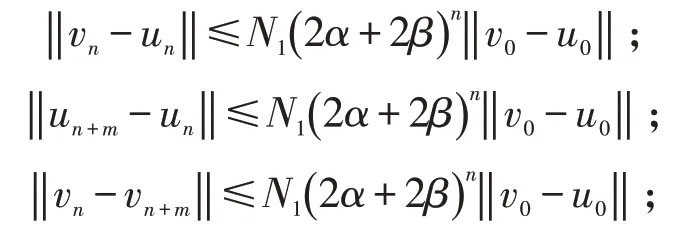
其中N1为P 的正规常数．又2(α+β)∈(0,1) ，于是{un} ,{ vn} 为E 中的Cauchy列．

下证u*为

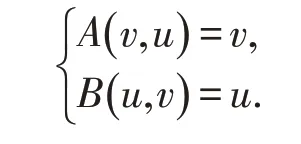
在[]u0,v0中唯一公共解．

由vn+1≥un+1和条件（ii）得，

由A，B 的连续性，和un→u*,vn→u*(n →∞)，可得B(u *,u*) ≤B(u *,u*) +2α(u*-u*) ，即B(u*,u*) ≤A(u *,u*) .

由A，B 为混合单调算子有，

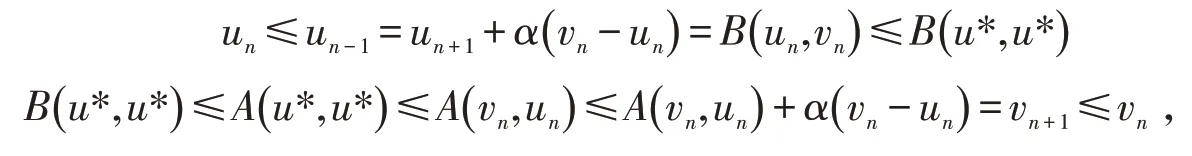
即

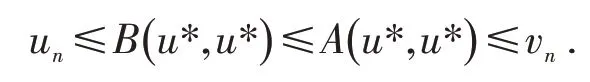
于是，θ ≤B(u *,u*) -un≤vn-un，由P 的正规性，有

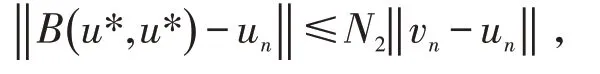
N2为P 的正规常数．

由上式可得

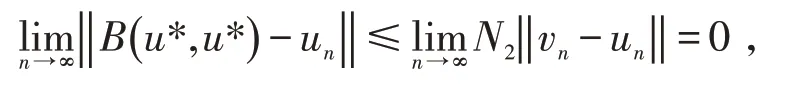
即

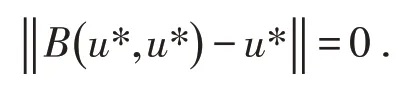
故B(u *,u*) =u*．类似可以证明A(u *,u*) =u*．即u*为

使用SRV 3/4”NPT螺纹型在线黏度计，根据稀释釜的尺寸和投料情况，准备适合长度的加长套管、法兰和内外丝连接头，从釜顶插入釜中，见图1。

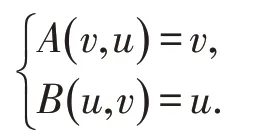
在[]u0,v0的公共解．

下证u*的唯一性．

设v*为（1.1）的另一个公共解．由迭代式（1）及A，B 为混合单调算子，类似可以得到

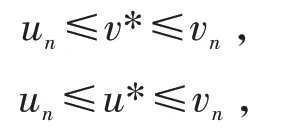
由上式可得

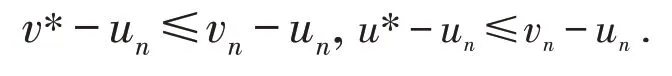
由P 的正规性，有

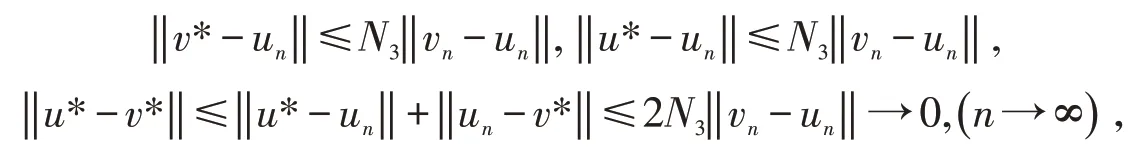
故u*=v*．唯一性得证．

由

令m →∞，得到误差估计为

类似有

将增算子看成是一种特殊的混合单调算子，于是有以下结论．

定理2 设E 为完备的锥度量空间， A:[]u0,v0→E， A 为增算子，且满足下列条件：（i）存在常数β ∈(0,1) ，使得Av-Au ≤2β(v-u)，∀u,v ∈[u0,v0]，且u0≤u ≤v ≤v0；（ii） u0+α(v0-u0)≤Au0, Av0≤v0-α(v0-u0)，其中α ∈[0 ,1]，且则算子A 在[u0,v0]中有唯一的不动点u*．有误差估计

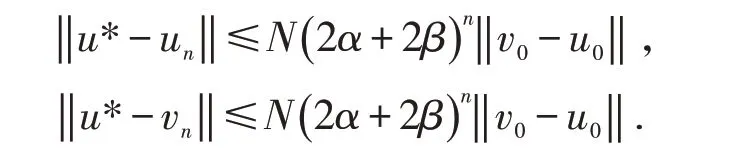
其中N 为P 的正规常数．

证明 构造迭代序列

类似定理1的证明，由归纳法知

由条件（i）有

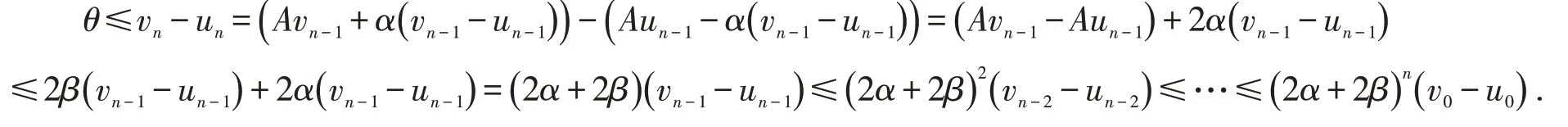
于是对于任意的自然数n,m，有

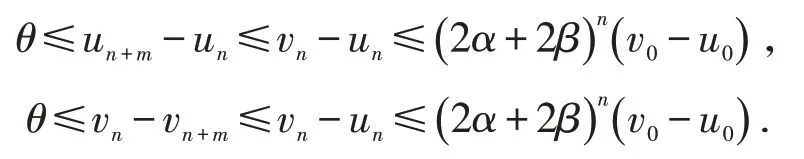
由P 的正规性有

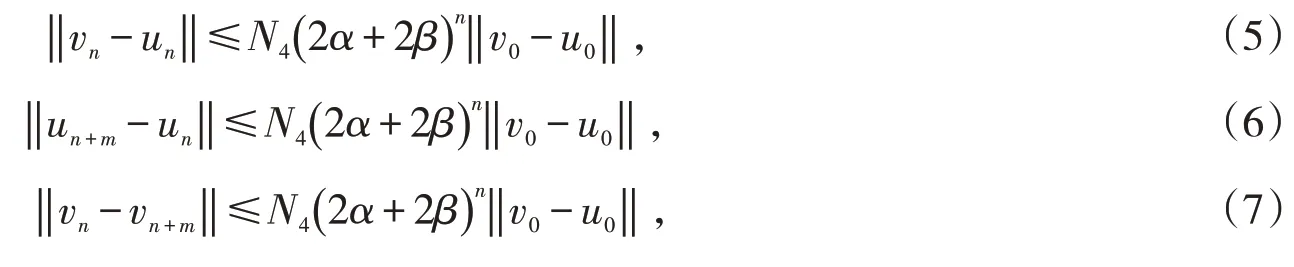
其中N4为P 的正规常数．

于是{un} ,{ vn} 为E 中的Cauchy列．由E 的完备性，所以存在，使得

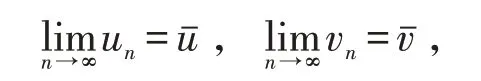
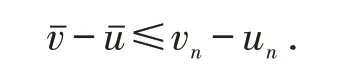
由P 的正规性和式（5），得到

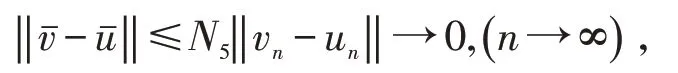
现证u*为A 在[]u0，v0中的不动点．由A 为增算子及迭代式（4），有

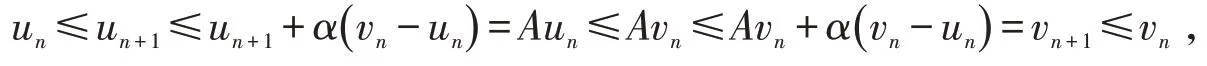
即un≤Aun≤Avn≤vn，得到Aun-un≤vn-un.

由P 的正规性，有

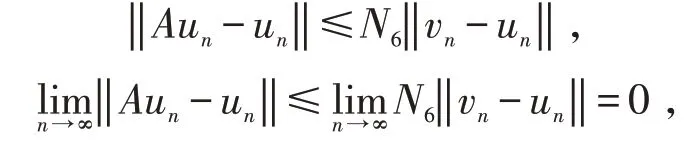
其中N6为P 的正规常数．

即得到

故Au*=u*，u*为A 在[]u0,v0中的不动点．

设v*也是迭代序列产生的另一个不动点，则有un≤v*≤vn．又由于un≤u*≤vn及P 的正规性，有

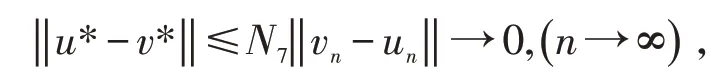
其中N7为P 的正规常数，故u*=v*．不动点的唯一性得证．

由‖ un+m-un‖≤N(2α+2β)n‖ v0-u0‖，令m →+∞，得误差估计为

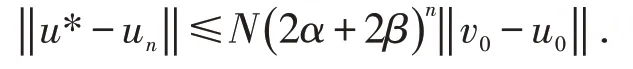
类似有

[1]GUO Da-jun,LAKSHMIKANTHAM V.Coupled fixed points of nonlinear operators with application[J].Nonlinear Analysis,TM A.,1987,11(5):623-637.

[2]孙经先．非线性泛函分析及其应用[M]．北京：科学出版社，2008.[3]郭大钧．非线性泛函分析[M]．济南：山东科技出版社，1985.

[4]郭大钧．非线性分析中的半序方法[M]．济南：山东科技出版社，2000：18-141.

[5]李国祯，朱传喜．关于混合单调算子的藕合不动点定理[J]．工程数学学报，1993，10（1）：9-16．

[6]许绍元．混合单调算子不动点存在唯一性定理及其应用[J]．吉首大学学报：自然科学版，2011,32（1）：11-13.

[7]盛梅波．一类减算子新的不动点定理及其应用[J]．南昌大学学报：理科版，2005，29（1）：35-37．

[8]GUO Da-jun,LAKSHMIKANTHAM V.Nonlinear problems in abstract cone[M].New York:Academic Press,1988.

[9]揭成文武，朱传喜．Menger PN-空间中两类混合单调算子新的公共不动点定理[J]．应用泛函分析学报，2011，13（1）：100-107．