捷联惯导基于地球系的动基座间接精对准算法
2014-10-24江一夫严恭敏
谢 波,江一夫,严恭敏,陈 勇
(1. 西安航天精密机电研究所,西安 710100;2. 西北工业大学自动化学院,西安 710072)
捷联惯导基于地球系的动基座间接精对准算法
谢 波1,江一夫1,严恭敏2,陈 勇1
(1. 西安航天精密机电研究所,西安 710100;2. 西北工业大学自动化学院,西安 710072)
为了将惯性凝固思想延伸到行进间精对准中并提升计算效率,提出了基于地球系的间接精对准算法。描述了地球系下的捷联惯导/里程计系统模型和相应的Ψ角误差模型。考虑安装偏差角、杆臂等因素,建立了相应的卡尔曼滤波方程。六组行车轨迹的行进间对准结果表明,相对于地理系精对准算法,地球系间接算法整体对准性能更加优越,系统的稳定性和快速性得到提高,在对准第600 s方位失准角可以稳定在 1 mil(1σ)的误差限内。另外,地球系滤波算法具有更好的初始化参数适应性,有利于工程实现。
行进间对准;地球坐标系;里程计;卡尔曼滤波
惯导系统受限于工作环境,往往需要在动态条件下完成初始对准。行车状态下的对准不可避免地需要外部设备提供的载体运动信息以滤除行进状态下的机动加速度和干扰加速度[1]。由于里程计(OD)输出噪声小、成本低廉、安装简易,同时与惯性传感器一样,具有自主、隐蔽、高采样率等特点,因而常作为车载惯性基定位定向系统的辅助信息源,本文也主要针对里程计辅助的车载捷联惯导系统行进间对准。
为了提高对准快速性并保证误差模型的鲁棒性,工程上的行进间对准遵循先粗对准后精对准的流程。文献[2-4]应用惯性凝固思想,较好地解决了动态条件下粗略姿态信息快速获取的问题。但对于后续精对准,绝大多数学者[5-7]都选择利用滤波算法直接估计相对地理系的姿态。为了将惯性系算法原理延伸到精对准中,文献[8-9]提出了引入惯性坐标系作为中间坐标系的间接算法,但两篇文献都没有说明这种算法的优势所在,也没有给出惯性系的重力模型和地球引力加速度误差模型,需要在不同坐标系之间的反复转换导航参数,这无疑增加了算法的繁复度和计算量。
事实上,地球系间接对准也是相对宏观空间的一种对准算法,地球相对惯性空间的单一自转角运动决定了地球系算法原理和惯性凝固思想在本质上的等同性。受此启发,本文详细推导了里程计辅助下的地球系间接精对准算法。一方面,地球系算法将粗对准中惯性凝固思想延伸到了精对准中,提升了精对准的鲁棒性和抗干扰性;另一方面,相对地理系算法,地球系的捷联解算和卡尔曼滤波运算可以分别提升40%和10%的计算效率[10],有利于在工程实践中实现一些复杂的高精度算法。
本文先推导地球系下的系统模型和卡尔曼滤波精对准模型,之后给出地球系间接精对准算法的详细运算流程,最后利用试验结果比较地理系算法和地球系间接算法的对准性能。结果表明地球系算法确实可以提升系统的快速性和稳定性,其整体对准性能更加优越,并且卡尔曼滤波器对初始化参数不敏感,有利于在工程上实现滤波参数的固化。
1 地球系下的系统模型描述
由于SINS/OD系统以地球系作为参考系,那么在新的坐标系下重新描述系统模型是非常必要的。以 e表示地球系,b表示捷联惯导坐标系,利用SINS输出量测可以写出e系地心位置矢量 re、e系地速 ve以及姿态矩阵的动态微分方程:
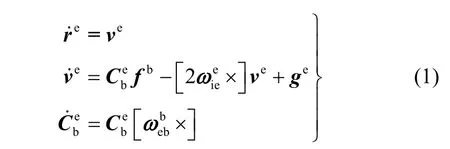
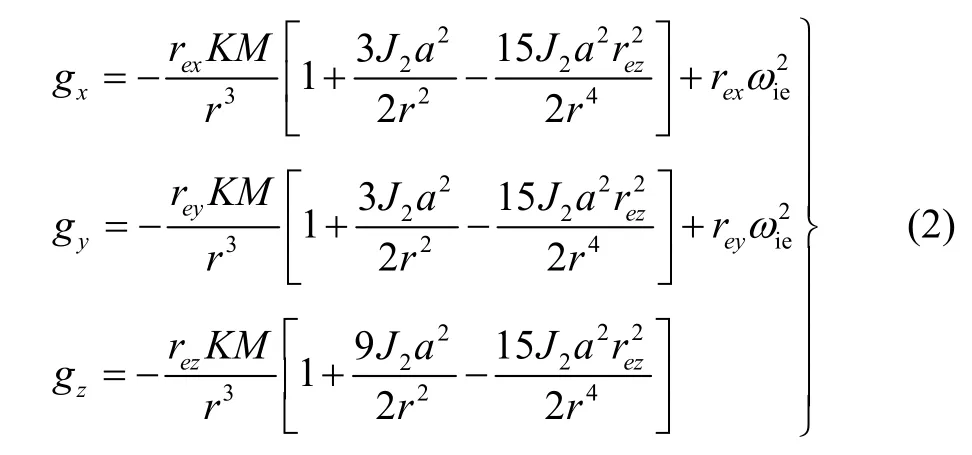
假设里程计和惯组刚性固联,以 m表示原点在OD安装轮轴中心的车体坐标系, lb表示m系原点相对 b系原点的安装杆臂,则里程计和捷联惯导之间存在如图 1所示的安装角度关系和位置关系。
里程计测量的是图1所示“o”点在m系的前向速度,同时考虑车辆运动约束,则里程计的输出 yod满足
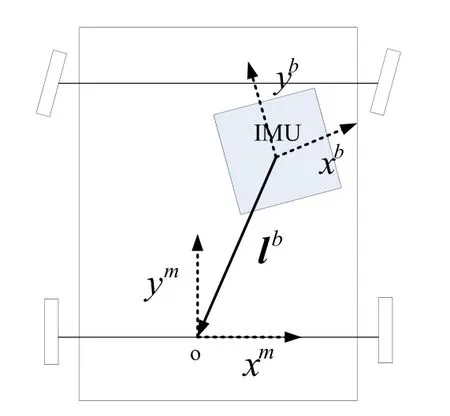
图1 惯组坐标系与车体坐标系的相互关系Fig.1 Relationship between IMU frame and vehicle frame
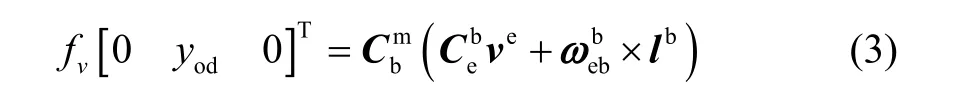
式中, fv表示将OD输出转换为载车前向速度的标度因数。假设m系相对b系存在俯仰安装偏差角 αθ、横滚安装偏差角 αγ和方位安装偏差角 αψ,此时式(3)可以改写为:
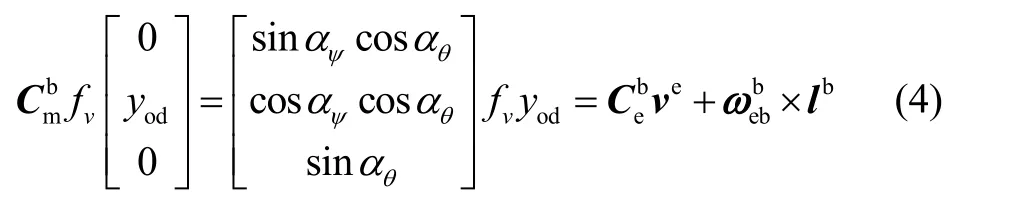
式(4)也说明横滚安装偏差角 αγ与OD量测无关。
2 地球系间接精对准算法
惯性导航系统误差模型是卡尔曼滤波器执行的数学载体,按照通用Ψ角误差模型,地球系下的捷联惯导误差传播方程可以表示为[11]:
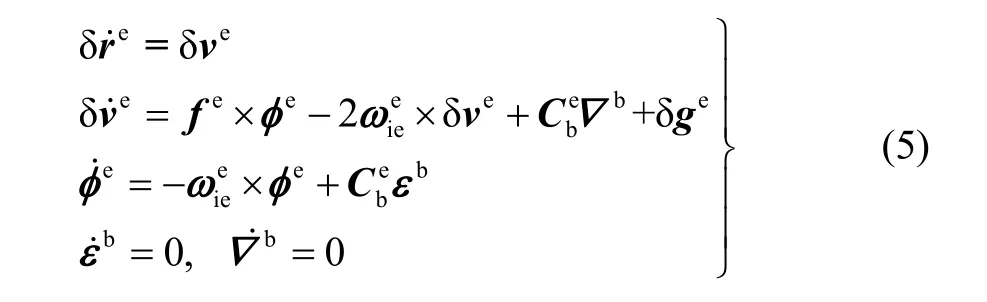
式中, δre表示地球系地心位置矢量误差, δve表示地球系地速误差,φe为姿态角误差矢量,εb、▽b分别为陀螺常值漂移和加计零偏。重力加速度误差矢量 δge由两部分组成:一是由不精确的瞬时载体位置计算重力加速度产生的计算误差 Δge;二是地球各点的扰动重力矢量 δgn,其中包括垂线偏差和重力异常。一般情况下忽略重力扰动矢量或者将其考虑为e系加计误差▽e的一部分,把两者作为一个整体来对待;重力加速度计算误差 Δge的一阶近似表达式可以写为:
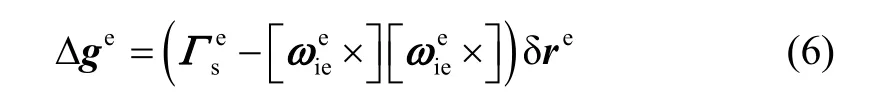
考虑到人员数量变动、车体减振等因素的影响,捷联惯导与里程计之间的姿态安装角是实时变化的;同时不同行驶路面条件、环境温度、轮胎状况和履带松紧将引起OD标度因数的变化。因此在建立Kalman滤波模型时,将安装偏差角估计误差矢量η和OD标度因数误差 Δfv作为状态量的一部分,实际中假设上述误差量为未知的随机常值,即:

而认为里程计与捷联惯导之间的安装杆臂在载车运行过程中变化不大,因此直接利用预标定结果,滤波过程中不再反馈校正。因此,选取如下18维状态量:
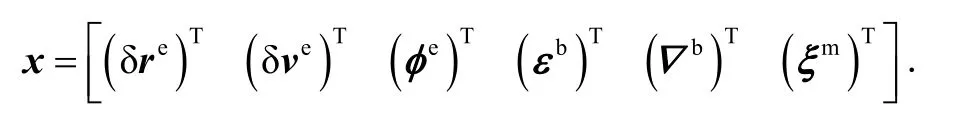
由IMU捷联解算e系速度可以计算得到图1所示“o”点的e系地速:
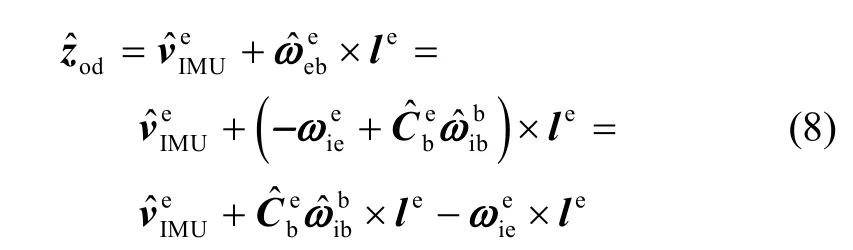
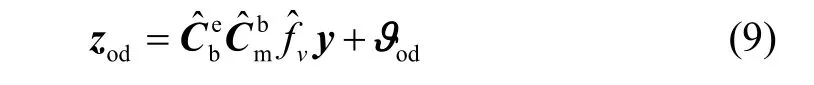
式中, ϑod为里程计的输入噪声,以两者速度之差作为观测量,同时忽略高阶误差项,可得:
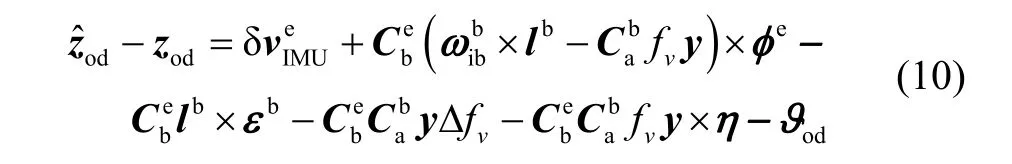
至此可以写出卡尔曼滤波器的系统方程和量测方程:
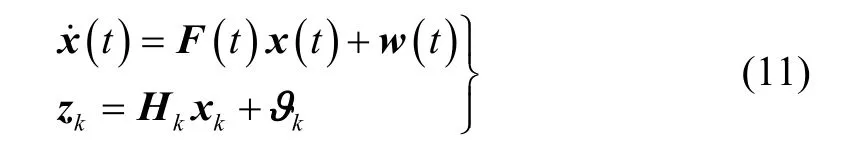
式中, F (t)为系统矩阵,可以由式(5)(7)得到; Hk为量测矩阵,可以由式(10)得到; w (t)、ϑk分别为系统噪声和量测噪声。
3 地球系间接精对准方案的具体实现
行进间精对准算法需要在已知粗略姿态信息的条件下才能达到线性最优,本文动态条件下的粗对准依然利用惯性凝固的思想来实现,在文献[2]中已经给出了具体算法。本文在100 s惯性系粗对准后初始化卡尔曼滤波器,之后切换到地球系行进间间接精对准开始实时姿态估计,同时反馈校正器件误差。最终相对地理系的姿态矩阵通过两个矩阵间接计算得到。

算法的具体流程如图2所示。
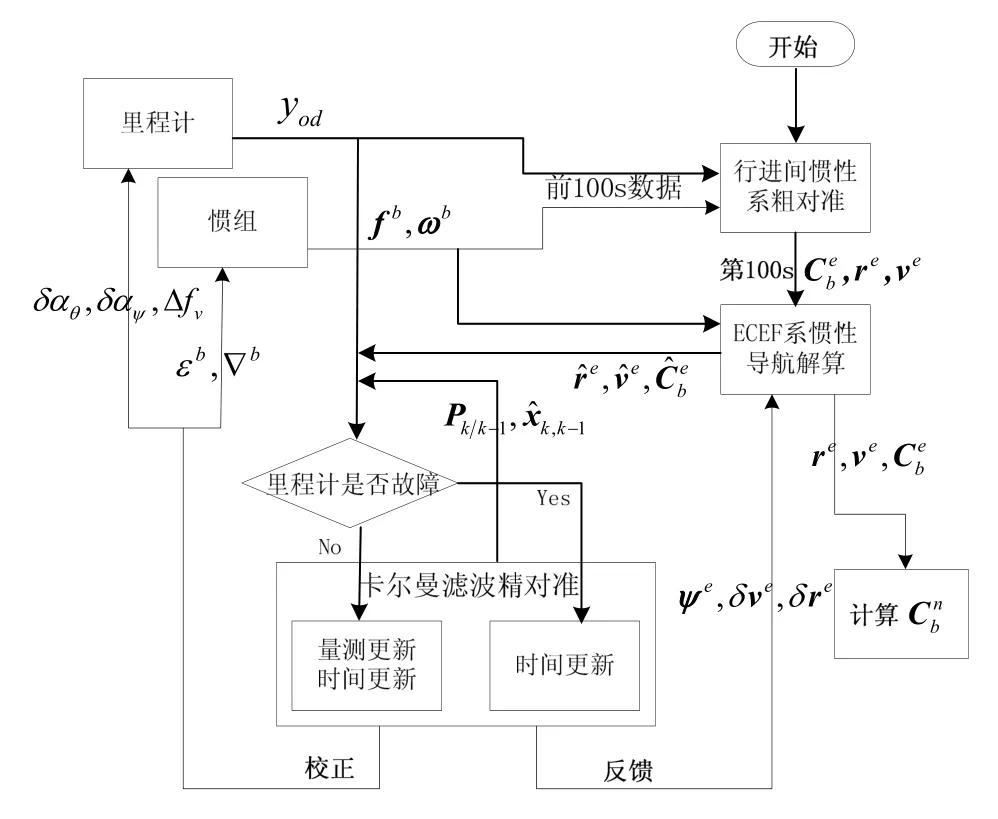
图2 ECEF系间接精对准算法的实现流程Fig.2 Flow chart of ECEF-frame indirect fine-alignment
4 实验验证
车载实验采用的惯导系统陀螺零偏为0.03 (°)/h,加计零偏在100 μg的水平,里程计分辨率约为43 mm/脉冲。为了验证地球系Kalman滤波精对准算法的有效性,分三次启电进行了三组车载实验,每组实验包括一段自由行车轨迹和一段矩形轨迹。图3给出了6段行车轨迹的具体路径,其中前三段轨迹为自由行车轨迹,后三段为设定的矩形轨迹,*和o分别表示轨迹的起讫点。
行进间对准从载车离开原点时刻开始,完成100 s惯性系粗对准后分别按照本文所提地球系间接算法和地理系算法开始精对准,且两种算法都采用各自固化的最优初始化参数。图4、5是以静止精对准转导航状态的姿态结果为参考值的方位失准角收敛曲线。
图4给出了前三组自由行车轨迹的方位失准角收敛曲线,图5为后三组矩形轨迹的方位角估计误差曲线。由图4和图5可以发现,对于轨迹2、5、6,地球算法的方位精度在170 s左右就已经稳定在相当高的一个水平,而地理系算法仍然存在大幅的误差波动。同样,对于轨迹 1、3、4,地球系间接算法的收敛趋势也要平稳得多。虽然两种算法在700 s左右对准精度基本一致,但是地球系算法能更早的稳定在1 mil(1σ)的误差限内。另外,离线处理轨迹数据可以明显发现,地理系滤波算法对初始化参数的变化非常敏感,小幅改变初始条件对系统性能影响很大,而地球算法却对滤波初始化参数具有很好的适应性,这也是地球系算法在工程应用上的优势所在。
以上结论说明,地球系间接精对准算法具有更好的鲁棒性和快速性。收敛过程中遇到量测扰动时,方位失准角不会出现大幅波动。基本上六组轨迹在对准第600 s就可以达到1 mil的方位对准精度。
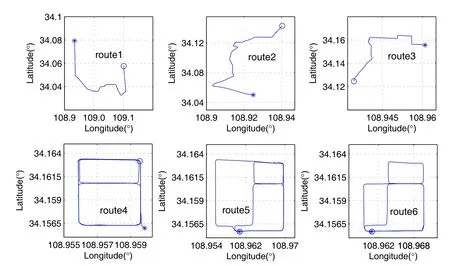
图3 车载实验行车轨迹Fig.3 Trajectory of vehicular test
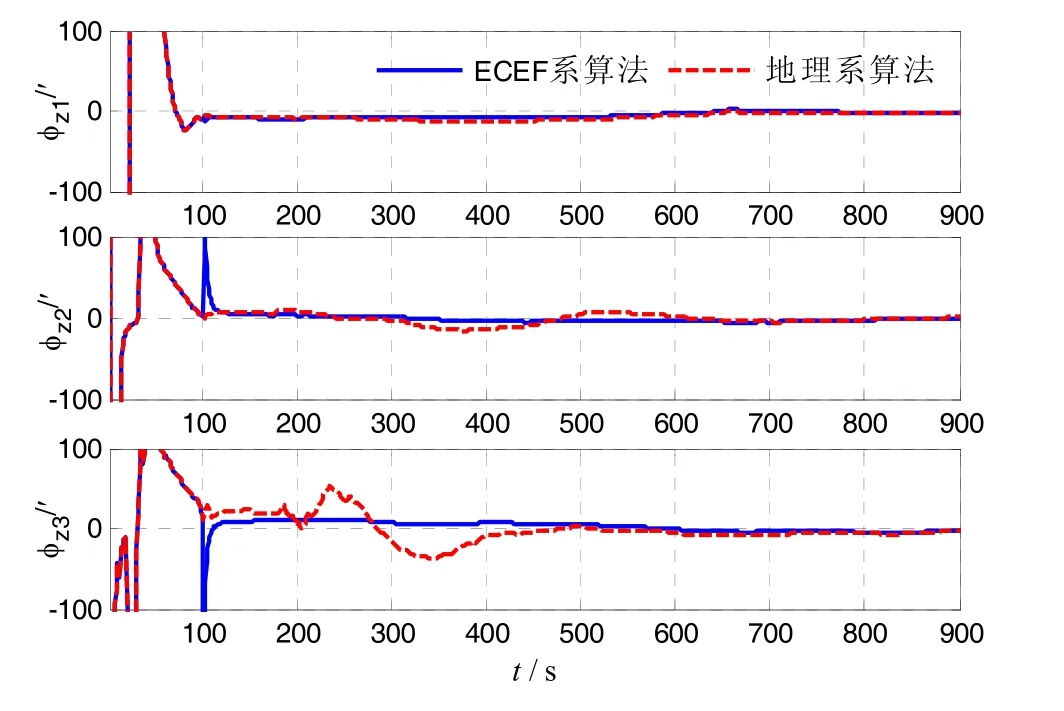
图4 三组自由行车轨迹的方位失准角Fig.4 Yaw errors of the three free traveling paths
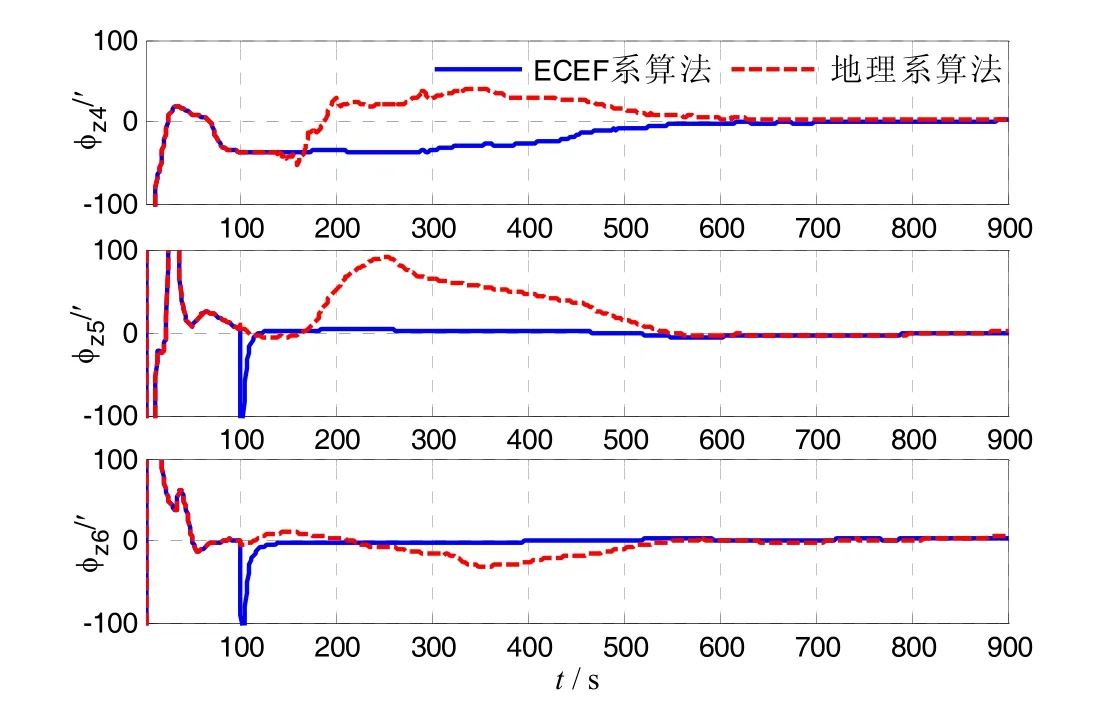
图5 三组矩形轨迹的方位失准角Fig.5 Yaw errors of the three rectangle paths
5 结 论
本文将惯性凝固算法原理延伸到了行进间精对准,为惯性系粗对准提出了一种基于地球参考系的后续间接精对准算法,提升了精对准卡尔曼滤波器的鲁棒性和抗干扰性。六组车载实验表明,相对地理系滤波算法,本文所提间接精对准算法收敛趋势更加平稳,稳定时间更短,极大地提升了整体对准性能。由实验结果可以看出,地球系算法在对准第600 s就能满足优于1 mil的方位对准精度要求。另外算法大幅提升了计算效率,对动态条件下滤波参数初始化的要求也宽松许多,有利于算法的工程实现。
(
):
[1] Silson P. Coarse alignment of a ship’s strapdown inertial attitude reference system using velocity loci[J]. IEEE Transactions on instrument and measurement, 2011, 60(6): 1930-1941.
[2] 严恭敏,翁浚,白亮,等. 基于惯性参考系的动基座初始对准与定位导航[J]. 系统工程与电子技术,2011,33 (3):618-621.
YAN Gong-min, WENG Jun, BAI Liang, et al. Initial in-movement alignment and position determination based on inertial reference frame[J]. Systems Engineering and Electronics, 2011, 33(3): 618-621.
[3] Wu Y X, Pan X F. Velocity/position integration formula part I: application to in-flight coarse alignment[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1006-1023.
[4] Jiang Y F, Xie B, Weng J. SINS in-motion alignment and position determination for land-vehicle based on quaternion Kalman filter[C]// The 32nd Chinese Control Conference. Xi’an, China, July 26-28, 2013.
[5] 肖烜,王清哲,付梦印,等. 里程计辅助陆用惯导行进间对准方法[J]. 中国惯性技术学报,2012,20(2):140-145.
XIAO Xuan, WANG Qing-zhe, FU Meng-yin, et al. INS in-motion alignment for land-vehicle aided by odometer[J]. Journal of Chinese Inertial Technology, 2012 20(2): 140-145.
[6] Seo J, Lee H K, Lee J G, et al. Lever arm compensation for GPS/INS/odometer integrated system[J]. International Journal of Control, Automation, and Systems, 2006 4(2): 247-254.
[7] Ali J, Ushaq M. A consistent and robust Kalman filter design for in-motion alignment of inertial navigation system[J]. Measurement 2009 42: 577-582.
[8] 缪玲娟,高伟熙,沈军,等. 基于惯性系采用 Kalman滤波的车载SINS行进间对准方法[J]. 兵工学报,2013,34(2):143-148.
MIAO Ling-juan, GAO Wei-xi, SHEN Jun, et al. SINS initial alignment algorithm base on inertial frame[J]. Acta Armamentarii, 2013 34(2): 143-148.
[9] 吴枫,秦永元,成妍. 基于GPS的弹载捷联惯导动基座传递对准技术[J]. 中国惯性技术学报,2013,21(1):56-60.
WU Feng, QIN Yong-yuan, CHENG Yan. Transfer alignment for missile-borne SINS using airborne GPS on moving base[J]. Journal of Chinese Inertial Technology, 2013 21(1): 56-60.
[10] Wei M, Schwarz K P. A strapdown inertial algorithm using an earth-fixed Cartesian frame[J]. Journal of the institute of navigation, 1990, 37(2):153-167.
[11] Godha S. Performance evaluation of low cost MEMS-based IMU integrated with GPS for land vehicle navigation application[D]. Calgary: University of Calgary, 2006.
Indirect fine-alignment algorithm of in-motion SINS based on ECEF-frame
XIE-Bo1, JIANG Yi-fu1, YAN Gong-min2, CHEN Yong1
(1. Xi’an aerospace precision electromechanical institute, Xi’an 710100, China; 2. College of Automation, Northwestern Polytechnical University, Xi’an 710072, China)
For the purpose of extending the application of inertia freezing methodology into moving-base fine-alignment and promoting computational efficiency, an indirect fine-alignment algorithm is presented which introduces earth-centered and earth-fixed (ECEF) frame as intermediate reference. The mathematical formulation of the inertial sensor/odometer integration system is given within ECEF frame, and the corresponding ψ-angle error model is outlined. By taking the SINS-vehicle misaligning angle and lever arm into account, the derivation of the appropriate Kalman filter (KF) is discussed. The proposed algorithm is verified through experimental data collected from six traveling routes. In comparison with geographic-frame KF algorithm, the ECEF-frame indirect approach has shorter stabilizing time and performs better in robustness, and a better overall accuracy of 1 mil(1σ) azimuth error within 600 s can be achieved. The ECEF-frame KF is less sensitive to changes of initialization parameters, which is useful for practical application.
in-motion alignment; ECEF frame; odometer; Kalman filter
1005-6734(2014)05-0593-04
10.13695/j.cnki.12-1222/o3.2014.05.007
U666.1
A
2014-05-18;
2014-09-03
国家自然科学基金(61273333);总装备部惯性技术预研基金(51309040501)
谢波(1978—),男,高级工程师,主要从事惯性导航技术研究。E-mail:reyoble@126.com
