无反馈的雷达网络系统误差协同配准方法

崔乃刚，张 龙，王小刚

（哈尔滨工业大学 航天工程系，哈尔滨 150001）

无反馈的雷达网络系统误差协同配准方法

崔乃刚，张 龙，王小刚

（哈尔滨工业大学 航天工程系，哈尔滨 150001）

在传统的雷达系统误差估计策略中，融合中心对雷达的观测数据进行处理，估计出系统误差并反馈给雷达对观测信息补偿误差。该策略会造成时延误差，不适于误差校准实时应用。为解决这一问题，构建了一种无需雷达观测信息和融合中心双向输入与反馈的雷达网络系统结构，提出了一种以雷达对目标状态估计信息为输入的系统误差协同估计算法。该算法采用扩展卡尔曼滤波对多雷达网络系统误差进行估计和配准。通过数学仿真，该方法对测角系统误差的估计精度达到了99%，目标的位置估计精度在系统误差补偿校正后达到96%，并且快速收敛。说明该方法能有效地估计出雷达的测角系统误差，并可直接校正和补偿雷达得到的状态估计信息，避免数据传输过程中产生的时延误差。

雷达组网；系统误差；协同配准；无反馈

现代战场中日益复杂的空情环境对防空预警系统提出了严峻的挑战，发展多雷达组网系统是有效解决该问题的途径之一，而雷达系统误差估计和校准是支撑雷达组网应用的关键技术[1]。

雷达系统误差估计一般分为两种方式：1）与理想数据比对方式[2]；2）多部雷达同时对同一目标的观测数据比对方式[3]。目前，对后者的研究较为深入，算法包括实时精度控制算法[4]、最小二乘法[5]，以及基于最大期望算法[6]（EM 算法）、极大似然法[7]的系统误差估计方法等。

徐惠群在文献[8]中针对分布式雷达—融合中心模式下的雷达系统误差估计问题，分析了在地心坐标系下和组网中心站的直角坐标系下的误差修正原理，给出了利用最小二乘算法和广义最小二乘算法进行误差修正的公式，并对实时质量控制算法、最小二乘算法、广义最小二乘算法和扩展卡尔曼滤波算法实现误差配准进行对比。吴泽民在文献[9]中基于数据链网络，提出了一种飞机与地面雷达的协同配准方法，利用能对自身精确定位的飞机构造虚拟雷达，获得配准的高精度基准源，实现对地面雷达的有效系统误差估计。虽然采用飞机进行雷达模拟，但本质仍然是组网雷达对同一目标协同观测。

为了实现雷达与ESM之间的配准问题，文献[10]将 ESM坐标系作为公共参考坐标系，提出采用扩维UKF[11,12]滤波方法实现雷达与ESM之间的误差配准，同时估计目标的运动状态和传感器的系统误差。崔亚奇在文献[13]中提出了扩展的MEX算法(EMEX)，并推广应用到多机动雷达情况下的系统误差估计中。文献[14]结合改进的相关函数序列设计了自适应卡尔曼滤波器，对海上多传感器平台的系统误差进行在线估计，减小了系统误差对多传感器数据融合精度的影响。

上述多雷达组网系统均采用有信息反馈的估计和配准方式，其雷达系统误差的估计和配准过程一般是：1）组网雷达将观测信息和状态估计信息传输给融合中心；2）融合中心采用最小二乘法或者卡尔曼滤波方法对雷达观测数据进行处理，估计出雷达的系统误差；3）融合中心将系统误差反馈给雷达；4）雷达使用系统误差对测量信息直接补偿以提高定位精度。

但在实际应用中，为了避免数据传输过程中的时延误差，并减小数据量，雷达不向融合中心传输观测数据，融合中心也不向雷达反馈系统误差，即雷达组网系统是无反馈的，在融合中心内同时完成雷达的系统误差估计和对雷达估计结果的补偿。因此，有必要对无反馈的雷达组网系统误差配准问题展开研究。

本文针对无反馈的多雷达组网系统误差配准问题，首先构建无信息反馈的多雷达组网结构，提出一种基于多雷达对目标状态估计信息的系统误差协同配准方法。为了满足系统实时性的需求，采用扩展卡尔曼滤波方法实时估计雷达系统误差，并对雷达的跟踪结果进行误差补偿和校准，以提高估计精度。仿真结果证明，本算法在保证雷达配准的效率和精确性的同时，更加贴近工程需求。

1 问题的描述

对无反馈雷达组网系统而言，组网雷达仅向融合中心传送对目标的状态估计信息，不传送雷达的观测信息，如测角和测距；融合中心不向雷达反馈系统误差信息。在这种情况下，融合中心只能根据雷达传输来的目标信息估计雷达的系统误差，并对估计信息进行校正以消除雷达系统误差的影响。

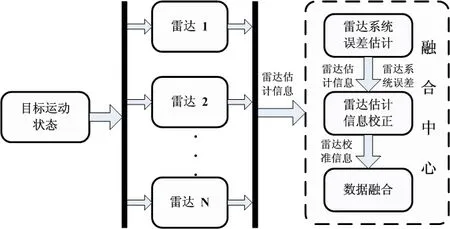
图1 无反馈雷达组网系统误差校准示意图Fig.1 Collaborative registration diagram for radar system error by feedback-free radar network

如图1所示，雷达系统误差的估计和配准在无反馈雷达组网系统中的一般过程如下：1）组网雷达将状态估计信息传输给融合中心；2）融合中心采用最小二乘法或者卡尔曼滤波方法对雷达估计信息进行处理，估计出雷达的系统误差；3）融合中心使用系统误差对估计信息补偿以提高定位精度。

为便于讨论系统误差的校准问题，假设组网雷达传送到融合中心的信息已经在时间上对齐，并且融合中心已完成对目标的航迹关联。雷达对目标的跟踪坐标系以及数据融合中心均为地球固连坐标系。不失一般性的，本文对含有两部地基雷达网络的系统误差校准方法进行详细推导。

2 系统误差配准模型

2.1 配准算法

假设两部雷达的工作体制相同，雷达对目标的测量值是以雷达为坐标原点的极坐标值，为：

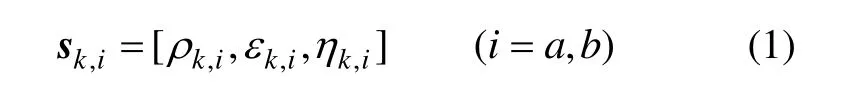
式中，ρ为目标测距，ε为目标高低角，η为目标方位角；k是采样的时刻，i是雷达的编号。则在以雷达为坐标原点的直角坐标系中，目标可以表示为：

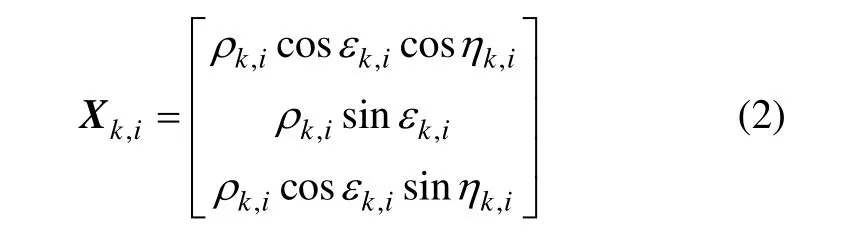
假设两部雷达的测量值均包含了系统误差和随机误差，随机误差满足高斯白噪声，系统误差保持很长时间不变，可看作常值。具体量测形式满足以下关系：

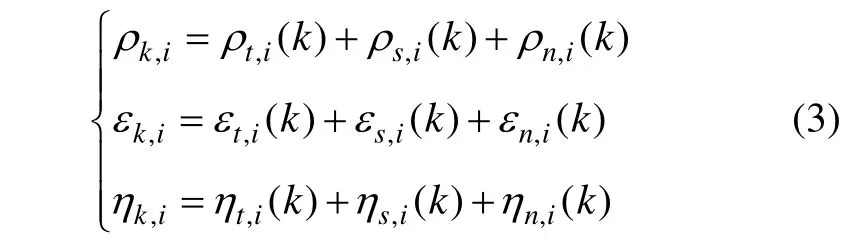
式中，下标 t,s,n分别表示真值、系统误差和随机误差。将目标在雷达直角坐标系中的坐标值转换到地心直角坐标系（ECEF）下，则有：

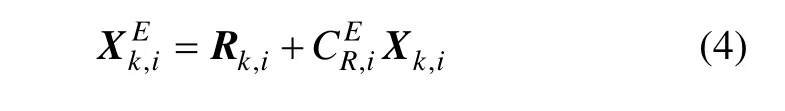
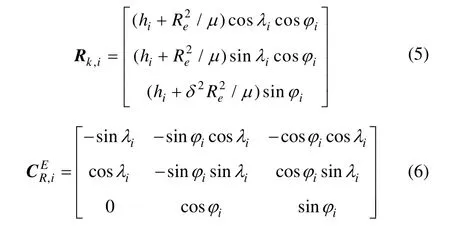
通过式(4)，将两个雷达分别得到的地心系下的坐标值作差，差值为：

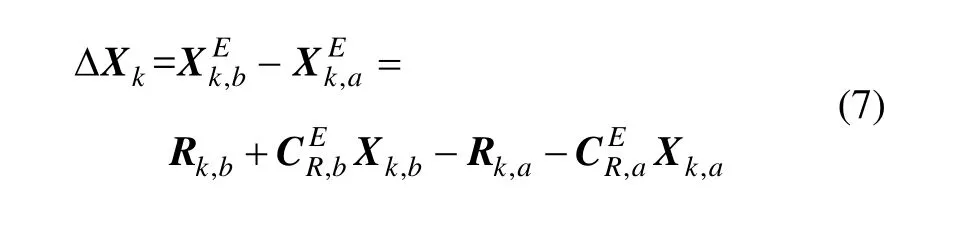
令式(2)在雷达真实观测值处对目标的局部直角坐标值进行一阶泰勒展开，忽略高阶项的影响，并且系统误差和随机误差相对测量值很小，则有：

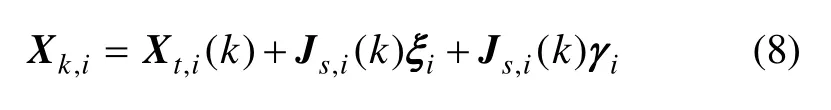
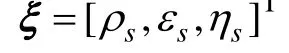
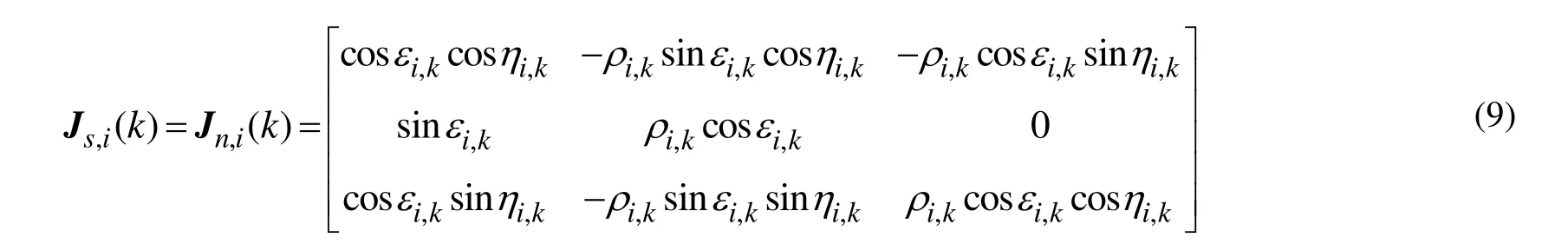
为了减少数据传输量，传送到融合中心的只有雷达对目标的估计信息而不包含雷达的观测数据，因此需要首先通过坐标变化将目标状态估计值转换到雷达直角坐标系下，再解算出雷达的极坐标观测值，进而求取上述雅可比矩阵。

由于系统误差和随机误差相对测量值很小，于是下式成立：

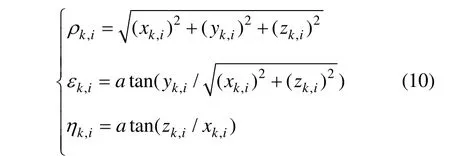
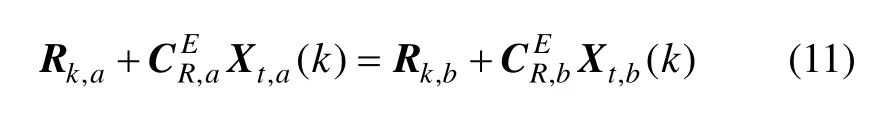
将式(8)和式(11)代入式(7)中，得到雷达观测误差与雷达系统误差和随机误差的关系有：

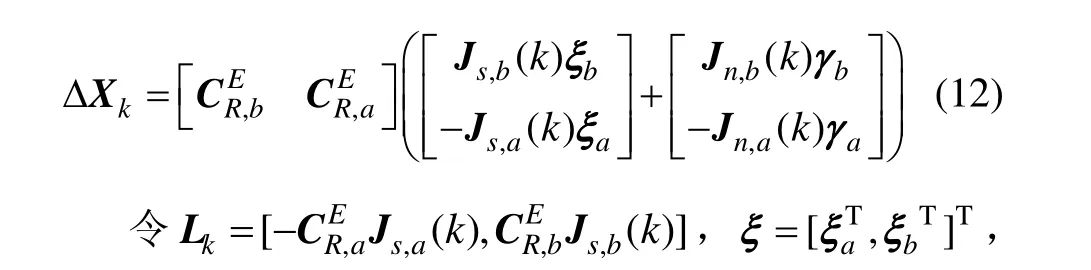
整理式(12)可得系统误差与随机误差的量测方程得到：

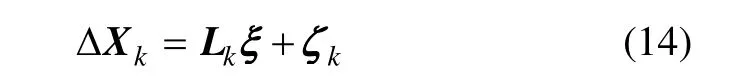
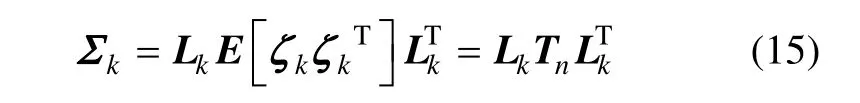
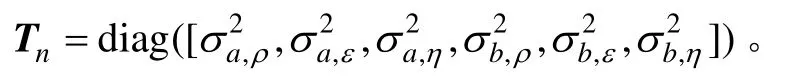
为了避免估计出的系统误差在传回雷达过程中出现时间延迟，同时可以实时地对雷达的估计结果进行校正，融合中心根据系统误差的估计结果可以通过下式对雷达的目标状态估计进行校正，公式为：

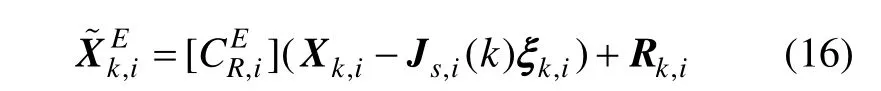
2.2 扩展卡尔曼滤波算法

2.2.1 状态方程

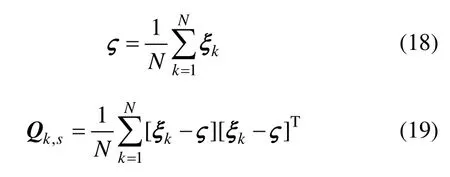
2.2.2 观测方程

根据式(14)，观测方程为：

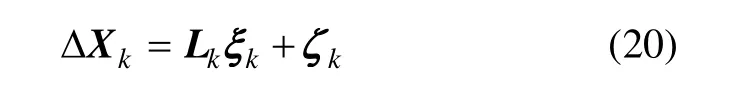
此式表明了两部雷达对目标的跟踪偏差与雷达系统误差和随机误差的关系。同时，也证明本方法的创新之处，即仅利用雷达对目标的估计结果就可以实现对雷达系统误差的估计。

2.2.3 EKF算法流程

根据扩展卡尔曼滤波算法[15]，选取系统误差状态变量初值 ξ0以及误差协方差矩阵 P0，则对雷达系统误差估计的扩展卡尔曼滤波算法流程如下：

时间更新方程：

1）一步状态预测值：

2）预测误差协方差：

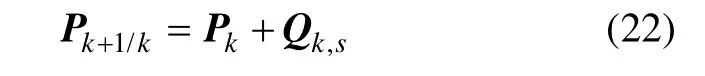
量测更新方程：

3）卡尔曼滤波增益：

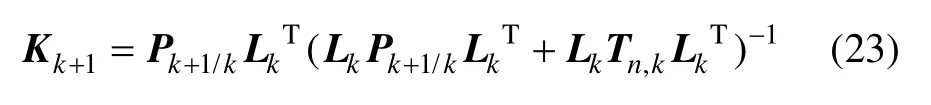
4）状态更新滤波值：

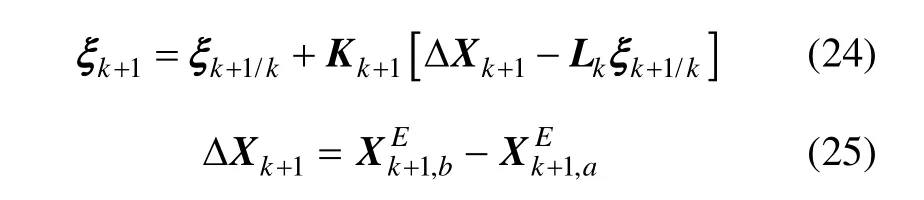
5）滤波误差协方差：

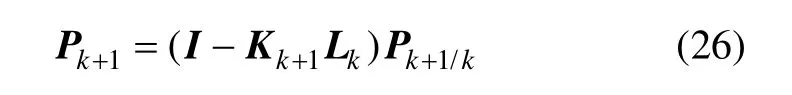
2.3 算法步骤

结合以上配准算法和EKF计算流程，对组网的两部雷达系统误差的校准步骤设计如下：

1）假定雷达a和雷达b同时对同一目标跟踪滤波，数据采样率与融合中心相同，忽略雷达向融合中心传输数据的时间延迟，则两部雷达的估计结果是同步的。

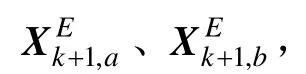
3）按照式(21)~(26)进行EKF计算，估计k时刻的系统误差向量。计算完成后返回(2)，继续下一个时间步长的计算。

4）设置误差配准开始时刻T，在该时刻对雷达的估计结果进行补偿。

3 数学仿真验证

本文采用两个预警雷达对同一弹道导弹目标进行跟踪。为了测试协同配准算法的性能，假定雷达和融合中心的时间同步已经完成，且雷达和融合中心的数据率相同，均为 0.1 s。设定雷达 1的地理坐标为（E115.74°, N29.43°, 5 m），雷达极坐标形式的系统误差是（20 m, 0.1°, 0.2°），随机误差的均根方为（10 m, 0.07°, 0.15°）；雷达2的地理坐标为（E114.11°, N30.71°, 5 m），雷达极坐标形式的系统误差是（20 m, 0.1°, 0.2°），随机误差的均根方为（10 m, 0.07°, 0.15°）。导弹目标在地心系下的初始状态为[-2664, 5350, 2870]Tkm，速度为[1700, 104, 1100]Tm/s。两部雷达同时对目标跟踪，并将估计结果传送到融合中心，忽略雷达数据处理时间和数据传输延迟。融合中心根据雷达对目标的跟踪结果估计雷达的系统误差，并在第80 s开始对雷达的估计结果进行补偿。仿真结果如图2~图10所示。

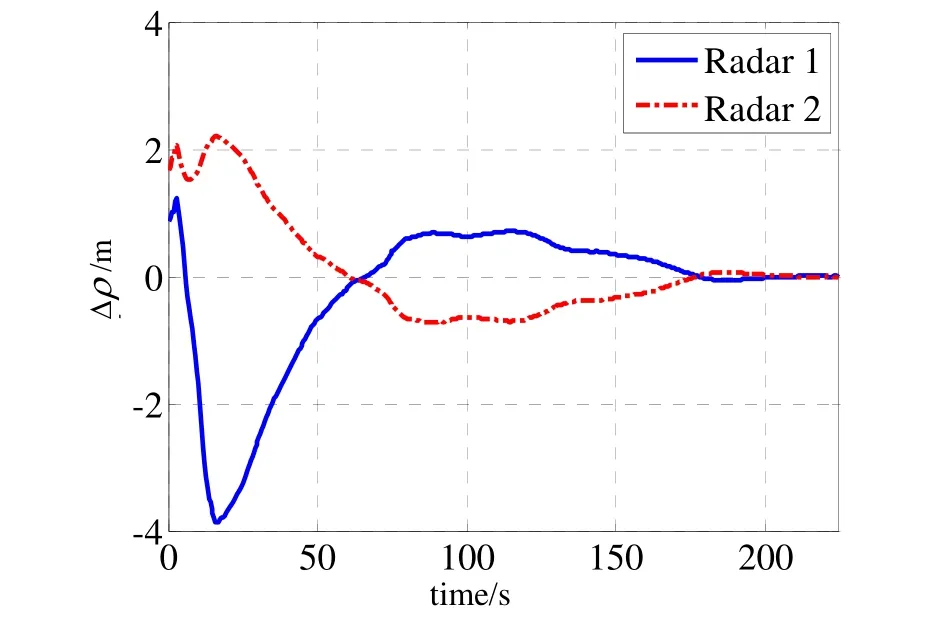
图2 雷达测距系统误差估计误差曲线Fig.2 Estimated error diagram of ranging system bias

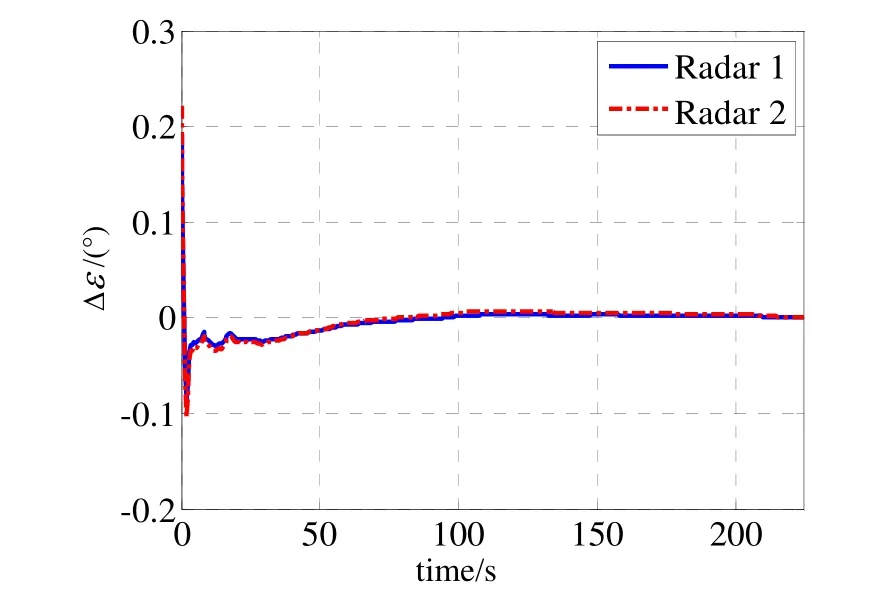
图3 雷达高低角系统误差估计误差曲线Fig.3 Estimated error diagram of pitch system bias

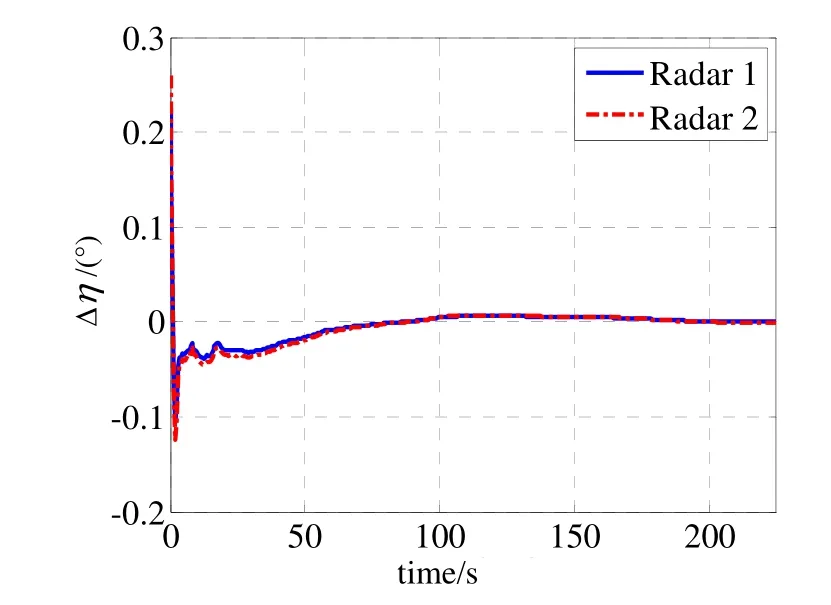
图4 雷达方位角系统误差估计误差曲线Fig.4 Estimated error diagram of azimuth system bias

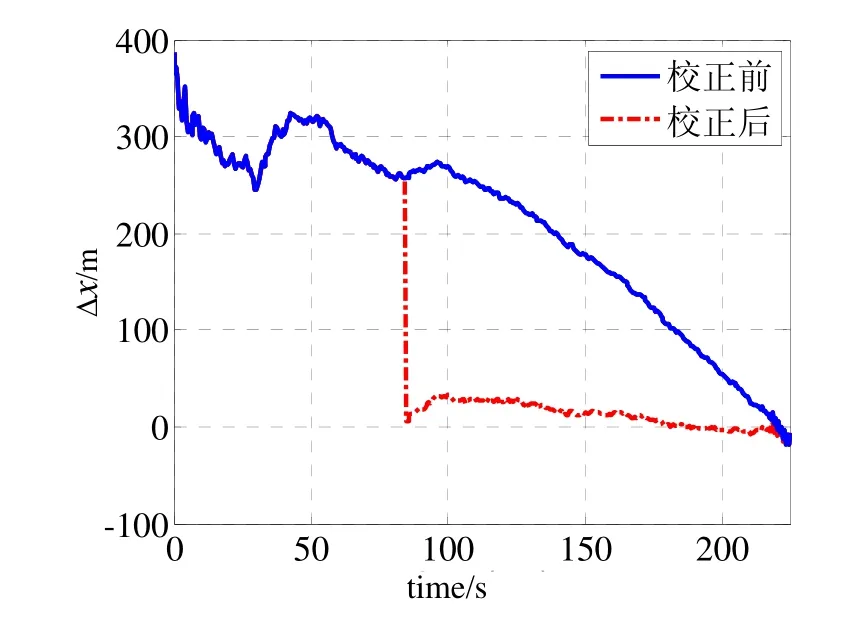
图5 雷达1 配准前后对目标x方向的位置估计误差Fig.5 Comparison of estimated position errors in x-coordinate between before and after registration by radar 1

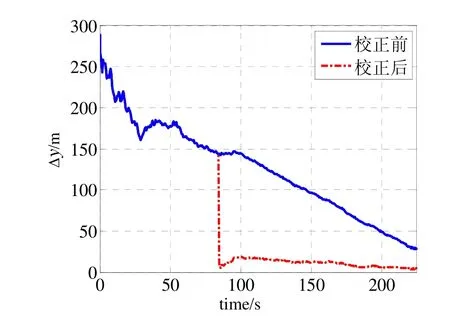
图6 雷达1 配准前后对目标y方向的位置估计误差Fig.6 Comparison of estimated position errors in y-coordinate between before and after registration by radar 1

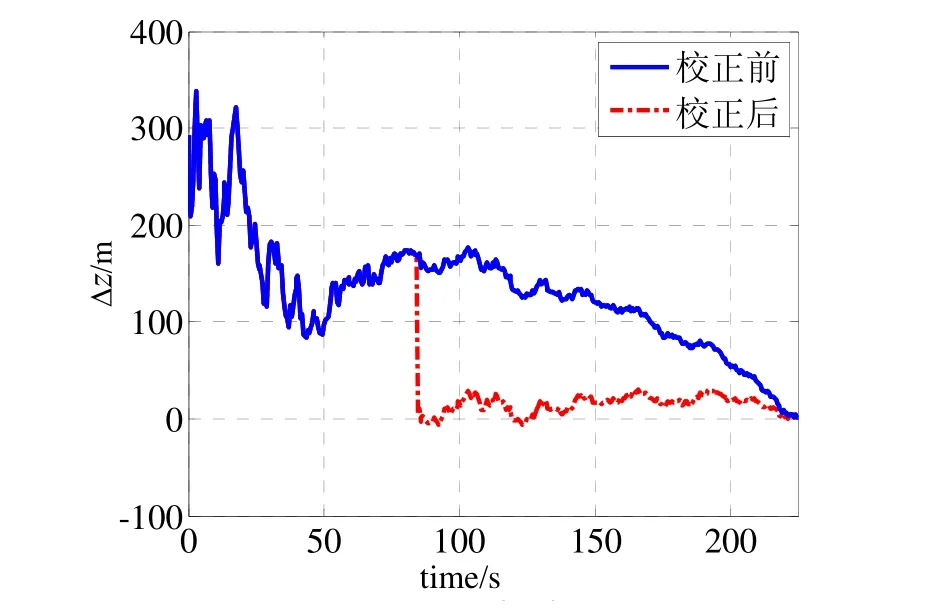
图7 雷达1 配准前后对目标z方向的位置估计误差Fig.7 Comparison of estimated position errors in z-coordinate between before and after registration by radar 1

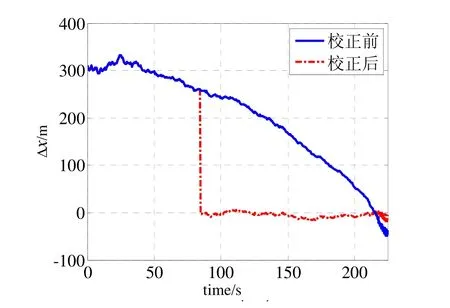
图8 雷达2配准前后对目标x方向的位置估计误差Fig.8 Comparison of estimated position errors in x-coordinate between before and after registration by radar 2

图9 雷达2配准前后对目标y方向的位置估计误差Fig.9 Comparison of estimated position errors in y-coordinate between before and after registration by radar 2

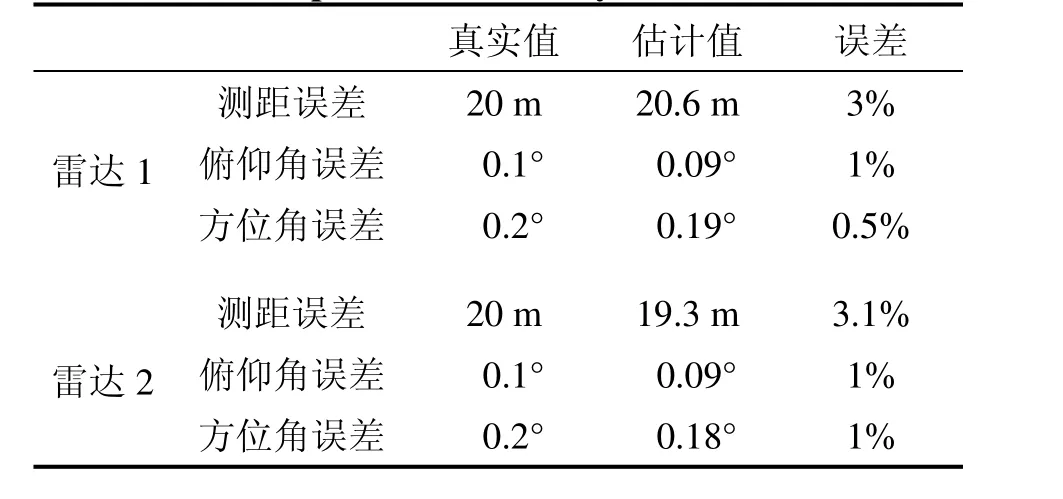
表1 80 s时系统误差的估计精度Tab.1 Estimated precision of radar system biases at time 80 s

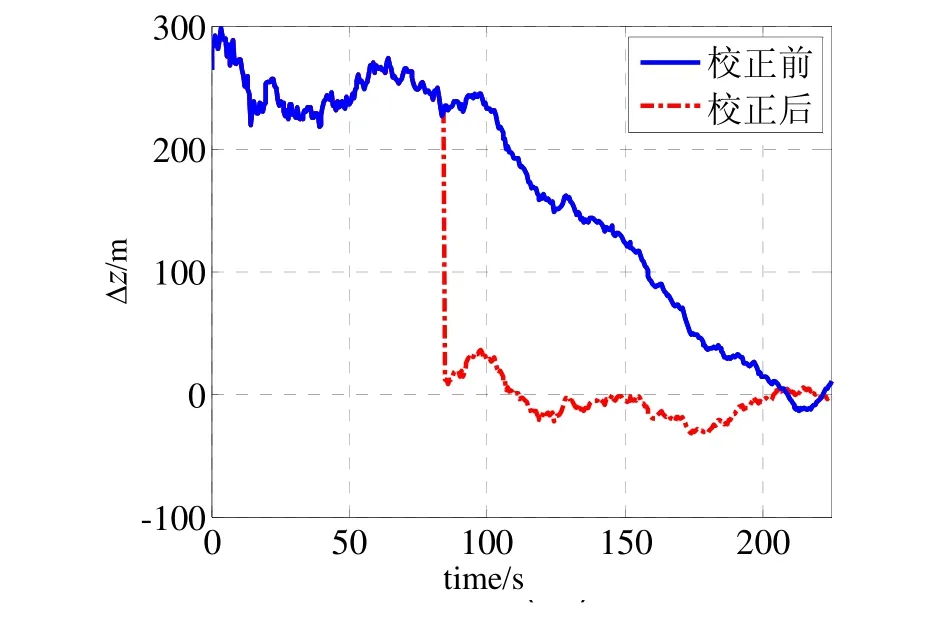
图10 雷达2配准前后对目标z方向的位置估计误差Fig.10 Comparison of estimated position error in z-coordinate between before and after registration by radar 2

图2显示了融合中心对两部雷达的测距系统误差的估计精度，经过170 s后两部雷达的测距系统误差才收敛，表明对测距系统误差的估计难度较大。图3~图4分别是对两部雷达的高低角和方位角系统误差的估计精度曲线，经过80 s误差完全收敛，表明对测角的系统误差估计精度较高。

表1为80 s时系统误差的估计结果。从表1可以清楚看到雷达1和雷达2测角系统误差的估计精度在80s时，达到了99%甚至更高的99.5%，而测距的估计精度稍低，为97%左右。

图5~图7同时显示了系统误差配准前后雷达1对目标的位置分量估计误差，在80 s时，校准前三个方向分量的雷达估计误差分别是260 m、145 m、170 m，校准后的误差分别是6 m、5 m、6 m，精度提高了96%以上。图8~图10同时显示了系统误差配准前后雷达2对目标的位置分量估计误差，在80 s时，校准前三个方向分量的雷达估计误差分别是265 m、125 m、230 m，校准后的误差分别是-3 m、3 m、7 m，精度提高了97%以上。从图中可以明显看到，在80 s开始对系统误差补偿校正，目标的位置估计精度迅速提高，并且快速收敛。

4 结 论

本文针对无反馈的多雷达组网系统误差配准问题，构建了无信息反馈的多雷达组网结构，根据雷达对目标状态的估计信息，采用基于EKF的协同配准算法有效估计雷达系统误差，同时不需要向雷达反馈系统误差估计结果，直接对雷达的估计信息校正补偿。仿真结果表明该方法提高了对目标的状态估计精度，有效地减小了雷达系统误差对状态估计的影响，解决了无反馈雷达网络的系统误差估计和雷达估计信息校准问题，避免了系统误差数据传输过程中造成的时延误差。因此，作为一种在线的雷达系统误差校正和配准方法，具有较高的工程应用价值。

（

）：

[1] Cheng long-He, Xia Zhu. System error registration algorithm for radar network using PSO[C]//IEEE: 2012 Fifth International Symposium on Computational Intelligence and Design(ISCID). 2012(1): 26-29.

[2] Ferry J P. Exact association probability for data with bias and features[J]. Journal of Advances in Information Fusion (S1557-6418), 2010(1): 41-66.

[3] Wu Z, Ren S, Liu X. Collaborative error registration algorithm for radar system[J]. Journal of China Ordnance (S1673-002X), 2009(3):198-202.

[4] 王波，王灿林，董云龙. RTQC误差配准算法性能分析[J]. 系统仿真学报，2006(11): 3067-3069.

WANG Bo, WANG Chan-lin, DONG Yun-long. Analysis of performance of RTQC registration algorithm[J]. Journal of System Simulation, 2006(11): 3067-3069.

[5] Fortunati S, Farina A, Gini F. Least squares estimation and Cramer-Rao type lower bounds for relative sensor registration process[J]. IEEE Transactions on Signal Processing(S1053-587X), 2011(3): 1075-1087.

[6] Li Zhen-hua, Chen Si-yue, Leung H. Joint data association, registration, and fusion using EM-KF[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010(2): 496-507.

[7] 朱洪伟，何友. 两坐标雷达组网中目标高度与系统误差联合估计[J]. 系统工程与电子技术，2013，35(9): 1861-1866.

ZHU Hong-wei, HE You. Joint estimation of target height and systematic error for two-dimensional radar network[J]. Systems Engineering and Electronics, 2013, 35(9): 1861-1866.

[8] 徐惠群，高秉亚. 组网雷达系统误差的估计原理与性能分析[J]. 现代雷达，2009，31(5): 39-42.

XU Hui-qu, GAO Bing-ya. Theory of system error estimation and its performance for network radar system[J]. Modern Radar, 2009, 31(5): 39-42.

[9] 吴泽民，任姝婕，刘熹. 雷达系统误差协同配准算法研究[J]. 兵工学报，2008，19(10): 1192-1196.

WU Ze-min, REN Shu-jie, LIU Xi. Research on collaborative registration algorithm for radar system error [J]. Acta Armamentarii, 2008, 19(10): 1192-1196.

[10] 刘德浩，王国宏. 基于UKF的雷达与ESM误差配准技术研究[J]. 电子测量技术，2011，34(6)：29-33.

LIU De-hao, WANG Guo-hong. Research on registration between radar and ESM using UKF[J]. Electronic Measurement Technology, 2011, 34(6): 29-33.

[11] Chang Lubin, Hu Baiqing, Li An, Qin Fangjun. Transformed unscented Kalman filter[J]. IEEE Transactions on Automatic Control, 2013, 58(1): 252-257.

[12] Liu Xing, Jiang Shoushan. Research on target tracking based on unscented Kalman filter[C]//Sensors & Transducers, 2013, 153(6): 13-21.

[13] 崔亚奇，宋强，何友. 基于改进 EX 的机动雷达误差配准算法[J]. 宇航学报，2011，32(4)：903-910.

CUI Ya-qi, SONG Qian, HE You. A modified exact method-based mobile radar registration algorithm[J]. Journal of Astronautics, 2011, 32(4): 903-910.

[14] Zhang Pixu, Wang Hangyu, Shi Zhangsong. Registration algorithm of multi-sensor system errors based on highprecision navigation equipments[J]. Advances in Computer Science and Information Engineering, 2012, 169(2): 375-380.

[15] 郭瑶，吴文启，罗兵，唐康华. 加速度辅助的EKF跟踪环及时间延迟影响分析[J]. 中国惯性技术学报，2011，19(4): 462-466.

GUO Yao, WU Wen-qi, LUO Bing, TANG Kang-hua. Acceleration aided EKF-PLL and analysis of time delay effect[J]. Journal of Chinese Inertial Technology, 2011, 19(4): 462-466.

Collaborative registration algorithm for system errors of feedback-free radar network

CUI Nai-gang, ZHANG Long, WANG Xiao-gang
(Department of Astronautics Engineering, Harbin Institute of Technology, Harbin 150001, China)

In traditional estimation strategy for radar’s systematic errors, the radar’s measurement data are transferred to fusion center, and the estimation of system errors obtained by radar measurement is feedback to radars to compensate the new measurement data. This strategy would cause delay error, so it is not suitable for applying in real time calibration. To resolve this problem, a structure of network radar system without bidirectional inputs is built, in which the radar measurement and feedback of system error is not required. A new collaborative registration algorithm for network radar system error is proposed which uses estimation of target state as input, and the Extended Kalman Filter (EKF) is applied in this algorithm. Through the simulation, the estimation precision of bearing system errors is achieved to 99%, and the accuracy of target position estimation is improved by 96% after registration. It is demonstrated that the new algorithm has excellent estimation precision of radar’s bearing system error, the convergence performance after emendating state estimation is excellent, and it has no constraint on delay error in system transmission.

radar network; system error; collaborative registration; feedback free

1005-6734(2014)05-0649-06

10.13695/j.cnki.12-1222/o3.2014.05.018

TN953

A

2014-07-04；

2014-10-17

国家自然科学基金（61304236）

张龙（1987—），男，博士研究生，从事目标跟踪、飞行器制导等研究。E-mail：longtoulinchang@163.com

联 系 人：崔乃刚（1965—），男，教授，博士生导师。E-mail：cui_naigang@163.com