改进的强跟踪UKF算法及其在INS/GPS组合导航中的应用
2014-10-24胡高歌刘逸涵高社生
胡高歌,刘逸涵,高社生,杨 一
(西北工业大学 自动化学院,西安 710072)
改进的强跟踪UKF算法及其在INS/GPS组合导航中的应用
胡高歌,刘逸涵,高社生,杨 一
(西北工业大学 自动化学院,西安 710072)
针对标准 UKF缺乏对系统状态异常的自适应调整能力,导致滤波精度降低的问题,提出一种改进的强跟踪UKF算法。该算法采用假设检验的方法对异常状态进行检测,当系统状态发生异常时,对预测协方差阵引入次优渐消因子自适应的调整滤波增益,实现对系统真实状态的强跟踪。该算法中次优渐消因子的确定无需计算系统模型的雅克比矩阵,提高了传统强跟踪 UKF的实用性。将提出的算法应用于INS/GPS组合导航系统进行仿真验证,并与标准UKF进行比较,结果表明,在系统状态存在异常时,提出的带单重次优渐消因子的强跟踪UKF得到的东向、北向位置误差在[-13.7 m, 14.9 m]以内,带多重次优渐消因子的强跟踪UKF得到的东向、北向位置误差在[-10.0 m, 12.1 m]以内,滤波性能明显优于标准UKF,提高了组合导航系统的解算精度。
强跟踪滤波;无迹卡尔曼滤波;次优渐消因子;INS/GPS组合导航
惯性导航系统(INS)与全球定位系统(GPS)在误差传播性能上具有互补特征,前者长期稳定性差、短期稳定性好,而后者刚好相反,因此采用组合导航技术将二者有机结合起来,构成INS/GPS组合导航系统,可以提高组合导航系统的整体性能[1-2]。
当前,扩展卡尔曼滤波(Extended Kalman filter, EKF)被广泛应用于组合导航系统设计[3]。EKF的基本思想是围绕状态估值将非线性系统模型进行一阶Taylor展开,然后采用卡尔曼滤波算法进行计算。然而,EKF存在理论上的局限性:系统模型的线性化近似对系统状态的后验均值与方差引入较大的截断误差,当系统模型非线性较强时,滤波精度将严重降低甚至发散;Jacobian矩阵的求取复杂、计算量大,个别情形下Jacobian矩阵可能不存在;模型失配、存在未知干扰或状态突变等情况下,EKF鲁棒性差。
为了克服EKF的缺陷,学者们提出了Unscented卡尔曼滤波(Unscented Kalman filter, UKF)算法[4]。UKF的核心思想是采用Unscented变换对非线性系统状态的后验概率密度函数进行近似。与 EKF相比,UKF以二阶以上精度近似高斯非线性系统状态的后验均值与方差,且无需计算Jacobian矩阵,具有实现简单、滤波精度高以及收敛性好等优点[5-6]。然而,同EKF类似,UKF算法在模型不准确或状态发生突变的情况下鲁棒性不佳、跟踪能力差。
文献[7]基于新息向量的正交性原理提出了强跟踪滤波器(strong tracking filter,STF)的概念,STF与通常的滤波器相比具有以下优良特性:较强的关于模型参数失配的鲁棒性以及较低的关于噪声与初值统计特性的敏感性;极强的关于突变状态的跟踪能力,并在滤波器达到稳态时仍保持这种能力;适中的计算复杂性。因此,可以将STF的思想与UKF结合起来以弥补后者鲁棒性差的不足。文献[8]将STF与UKF相结合,设计了一种强跟踪UKF,并用于航天器自主导航,提高了系统的可靠性。文献[9]将强跟踪UKF应用于视觉跟踪,改善了非线性视觉跟踪的鲁棒性与跟踪精度。然而,以上强跟踪UKF都是通过引入单重次优渐消因子对预测误差协方差阵进行调整,对于复杂的多变量系统,上述算法无法保证对每个变量都具有很好的跟踪能力。文献[10]提出一种带多重次优渐消因子的强跟踪UKF,克服了带单重次优渐消因子的强跟踪UKF对多变量跟踪能力差的缺陷。然而,同文献[8-9]设计的两种算法一样,该算法中多重次优渐消因子的求取需要计算系统模型的Jacobian矩阵,给实际应用带来诸多不便。
针对标准 UKF缺乏对系统状态异常的自适应调整能力,导致滤波精度降低的问题,本文从强跟踪滤波的基本理论着手,结合UKF算法框架,推导了强跟踪UKF次优渐消因子的具体形式,并在此基础上提出一种改进的强跟踪UKF(improved strong tracking UKF, ISTUKF)滤波算法。与传统的强跟踪UKF不同,提出的ISTUKF中次优渐消因子的确定无需计算系统模型的Jacobian矩阵,便于实际应用。此外,该算法采用假设检验的方法对系统异常状态进行检测,以判断是否引入次优渐消因子对预测误差协方差阵进行调节。提出的ISTUKF有两种形式:带单重次优渐消因子与带多重次优渐消因子。将提出的 ISTUKF应用于INS/GPS组合导航系统进行仿真验证,结果表明:当系统状态存在异常时,ISTUKF滤波性能明显优于标准UKF;相比于带单重次优渐消因子的ISTUKF,带多重次优渐消因子的ISTUKF对不同的状态分量以不同的速率调节,因而精度更高。
1 标准UKF
考虑非线性离散系统
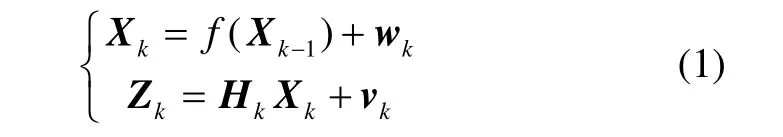
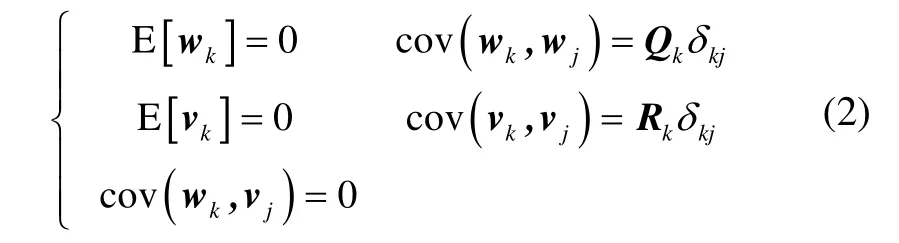
式中, Qk为非负定矩阵, Rk为正定矩阵, δkj为Kronecker-δ函数。
对于非线性系统(1),标准UKF滤波算法如下:① 初始化
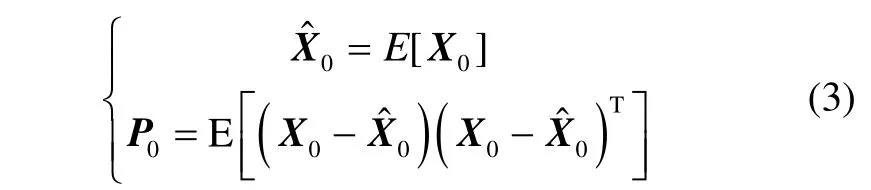
② Sigma点计算
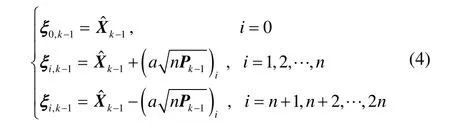
③ 时间更新
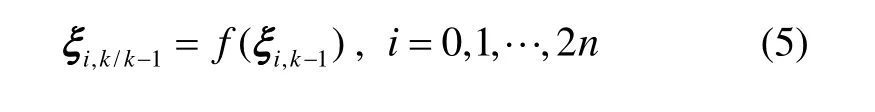
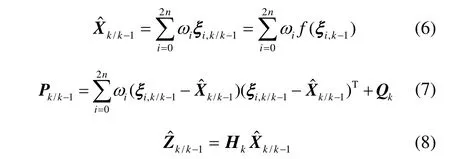
其中权值 ωi选取为:
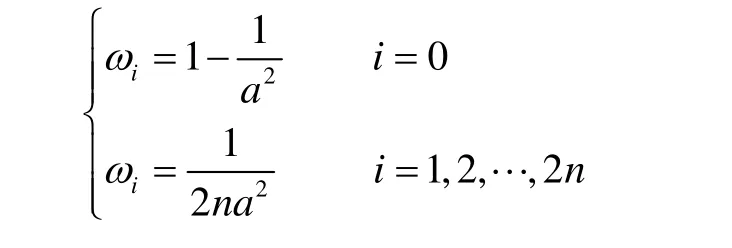
④ 量测更新
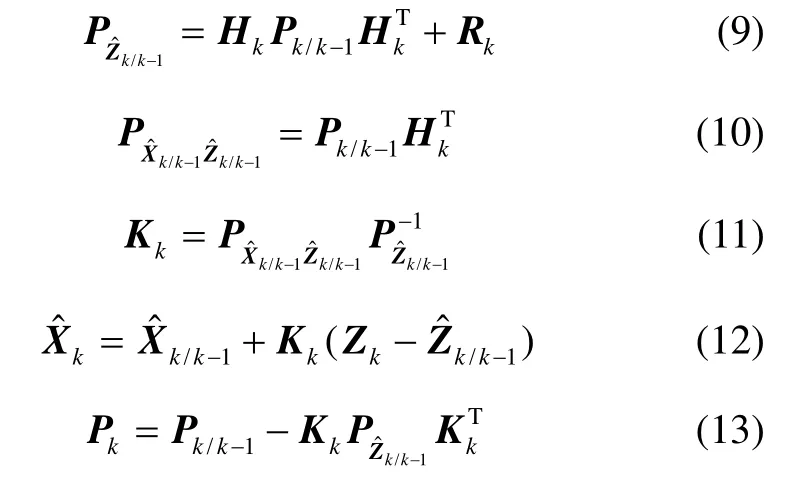
2 改进的强跟踪UKF
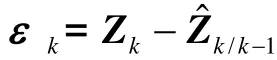
2.1 STF基本原理
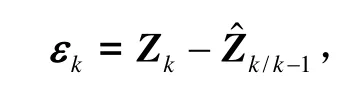
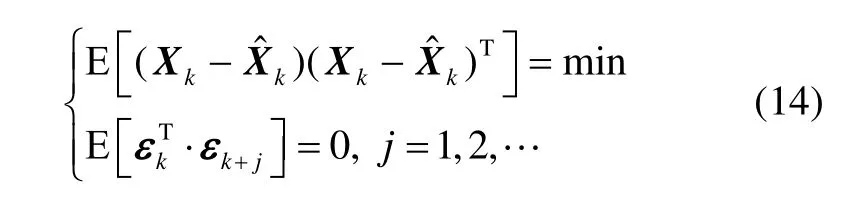
式中,第一个等式为滤波器实现最优估计的性能指标;第二个等式称作正交性原理,要求不同时刻的新息向量保持正交关系,且具有类似白噪声的性质,表明已将新息序列中的一切有效信息提取出来。强跟踪滤波器将新息序列的不相关性作为衡量滤波性能是否优良的标志。
2.2 ISTUKF次优渐消因子的确定
强跟踪UKF将次优渐消因子 λk引入预测协方差阵 Pk/k-1以提高系统的鲁棒性与自适应能力,具体为:
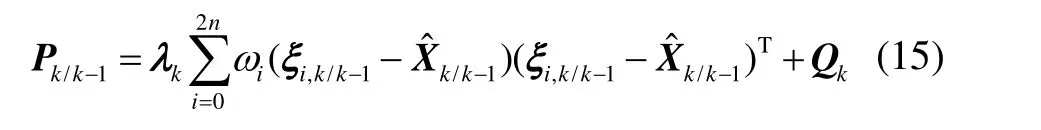
记UKF的估计误差与预测误差分别为:
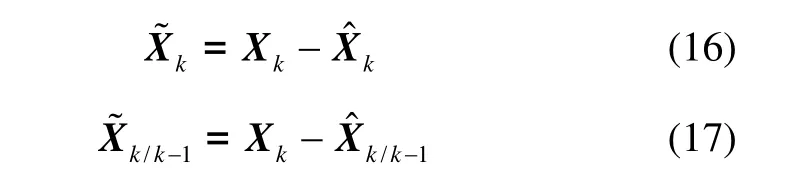
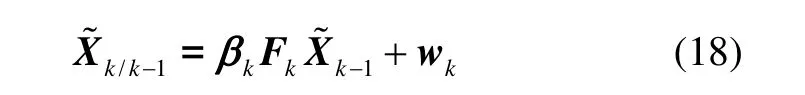
由式(1)(8)(18)可得新息序列:
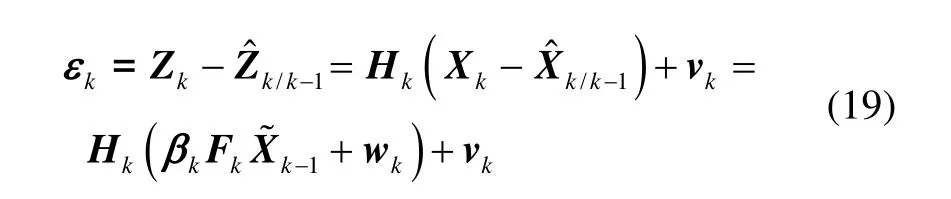
因而:
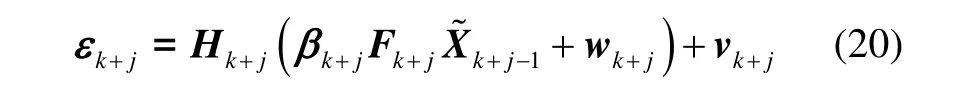
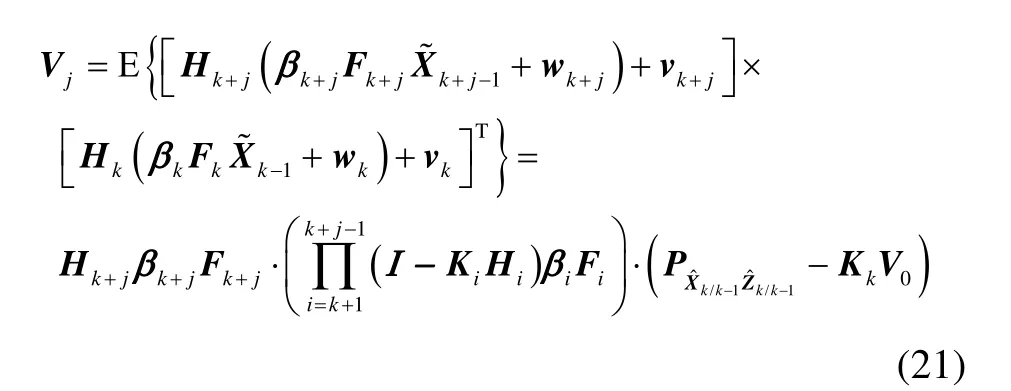
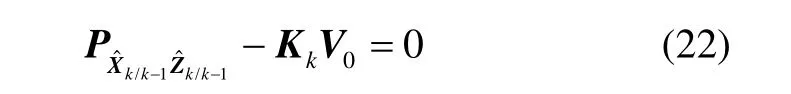
将式(9)-(11)代入式(22)有:
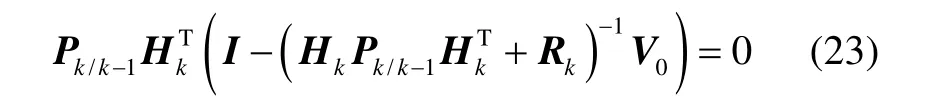
即:
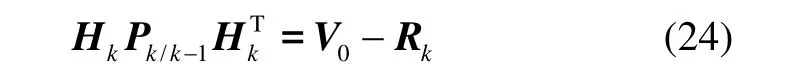
将修改后的预测协方差阵(15)代入式(24)可以得到:
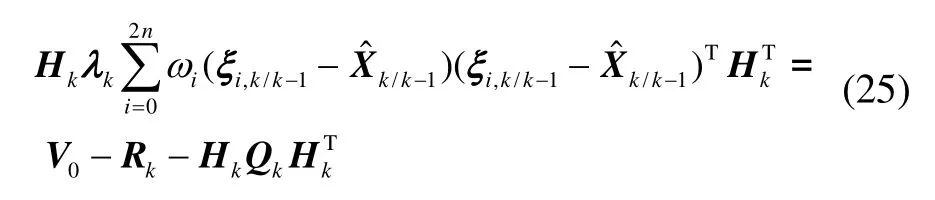
式(25)中 V0为滤波器实际输出的新息协方差阵,可根据下式计算:
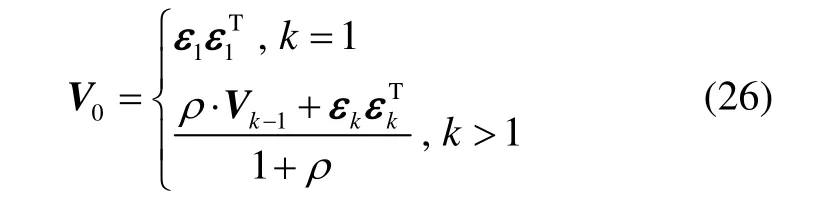
2.2.1 单重次优渐消因子
若次优渐消因子 λk为标量,对(25)求迹可得:
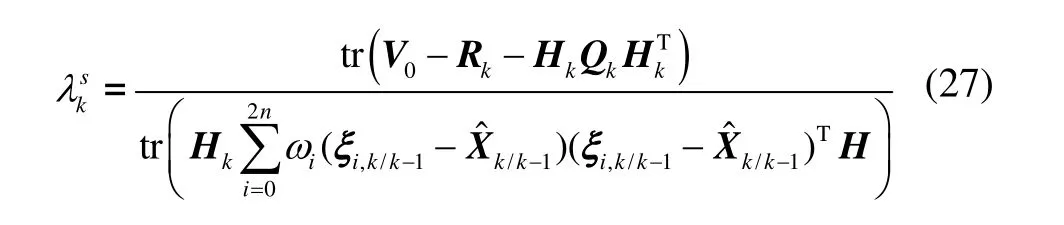
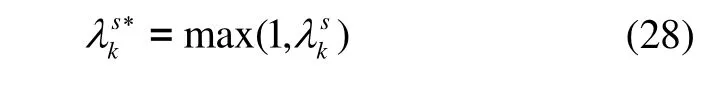
2.2.2 多重次优渐消因子
令
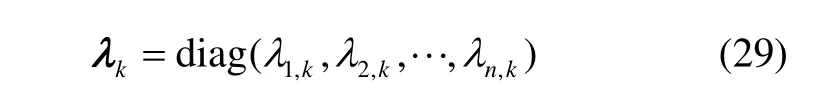
将(29)代入(25)并求解该矩阵方程,得其解:
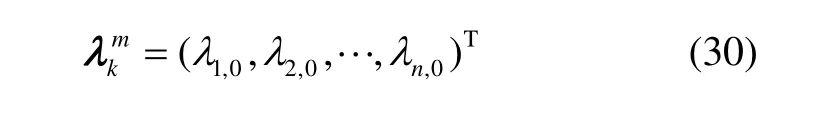
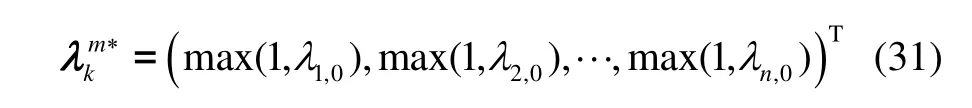
2.3 系统状态异常检测
ISTUKF中,修改后的预测协方差阵(15)仅在系统状态出现异常时采用,其他情形下仍使用式(7)进行计算。本节采用假设检验的方法,利用新息向量的统计信息,对系统异常进行检测。
定义统计量
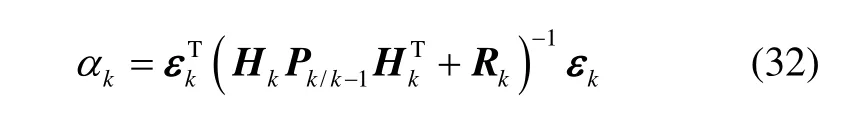
及以下假设:
零假设 γ0:系统正常工作;
备选假设 γ1:系统存在异常。
统计量 αk服从自由度为m的 χ2分布。对于取定的显著性水平α(0 < α≤1),由
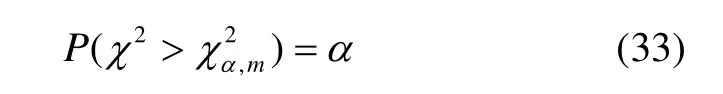
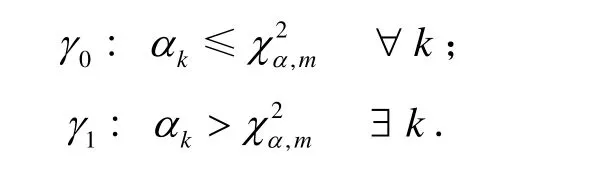
2.4 ISTUKF算法实现
对于非线性系统(1),提出的ISTUKF算法主要步骤如下:
① 采用式(3)对滤波算法初始化;
② 利用式(4)进行Sigma点计算;
③ 采用式(5)(6)计算状态一步预测;
④ 运用2.3节提出的方法对系统状态进行检测,若存在异常,采用式(15)计算预测协防矩阵,否则采用式(7)进行计算;
⑤ 采用式(8)-(13)完成时间更新的其余计算与量测更新;
⑥ 返回步骤②,进行下一时刻滤波解算。
3 仿真实验及分析
将提出的ISTUKF算法应用于INS/GPS组合导航系统进行仿真验证,并与标准UKF进行比较。仿真采用文献[2]中设计的INS/GPS组合导航系统模型。
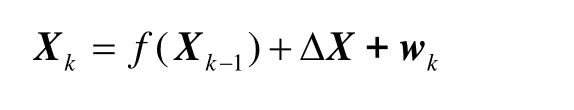
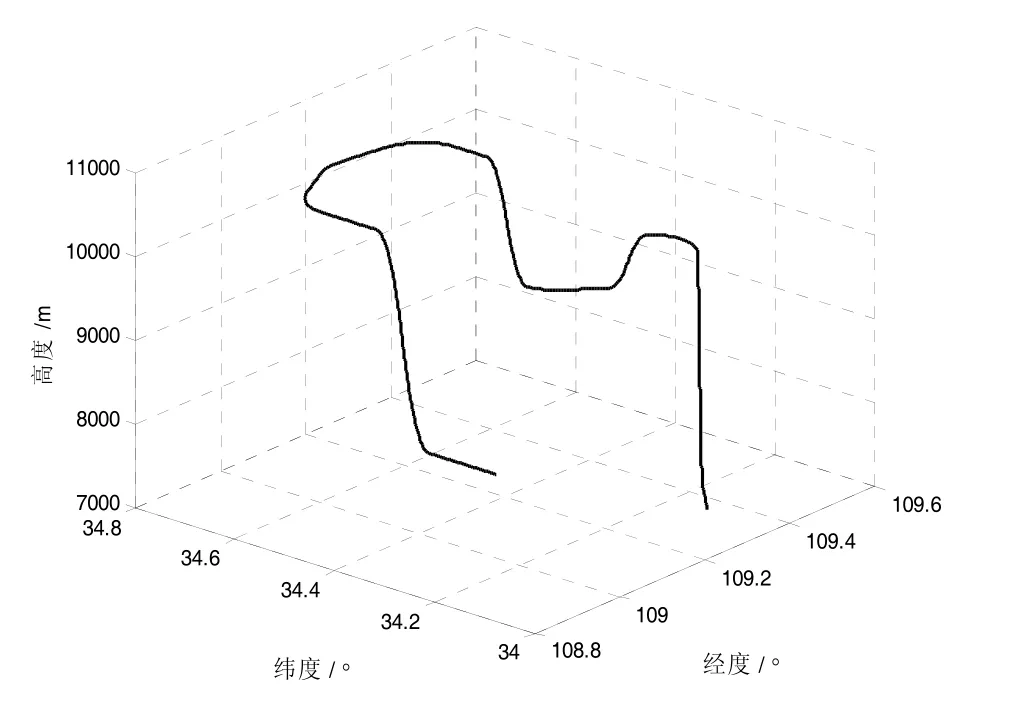
图1 飞机理想飞行轨迹Fig.1 Ideal flight trajectory of the aircraft
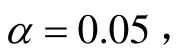
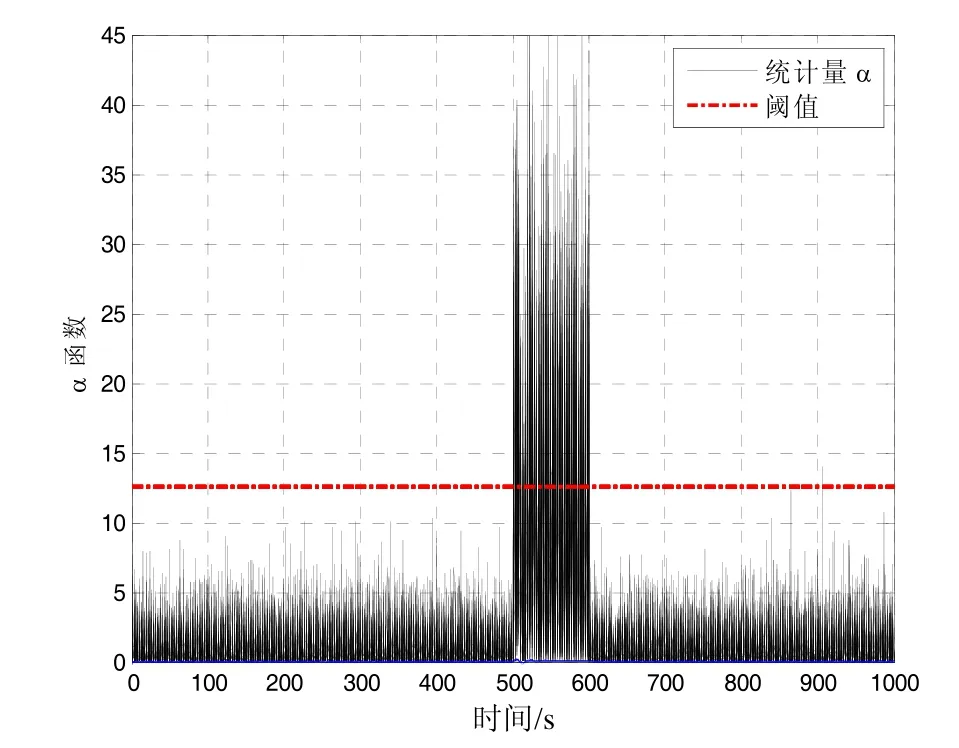
图2 采用标准UKF时 αk变化曲线Fig.2 Behavior of αk as the standard UKF is used

图3 采用单重次优渐消因子的ISTUKF时 αk变化曲线Fig.3 Behavior of αk as the ISTUKF with single suboptimal fading factor is used
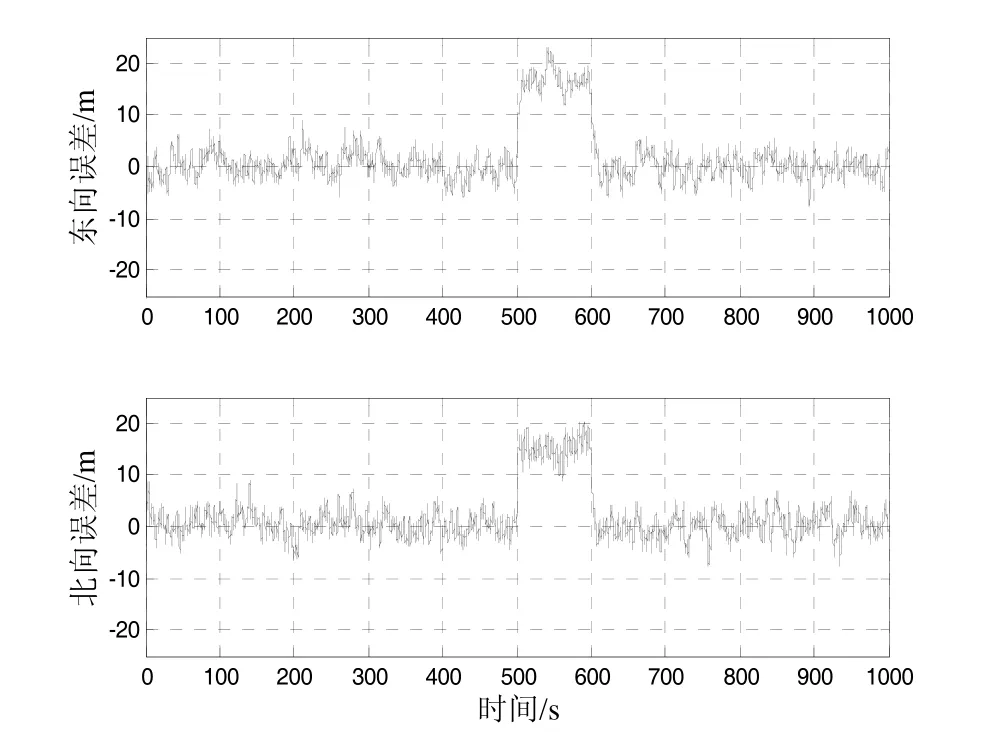
图4 标准UKF定位误差Fig.4 Position error of standard UKF
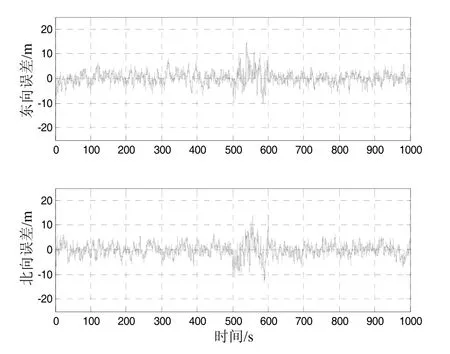
图5 带单重次优渐消因子的ISTUKF定位误差Fig.5 Position error of ISTUKF with single suboptimal fading factor
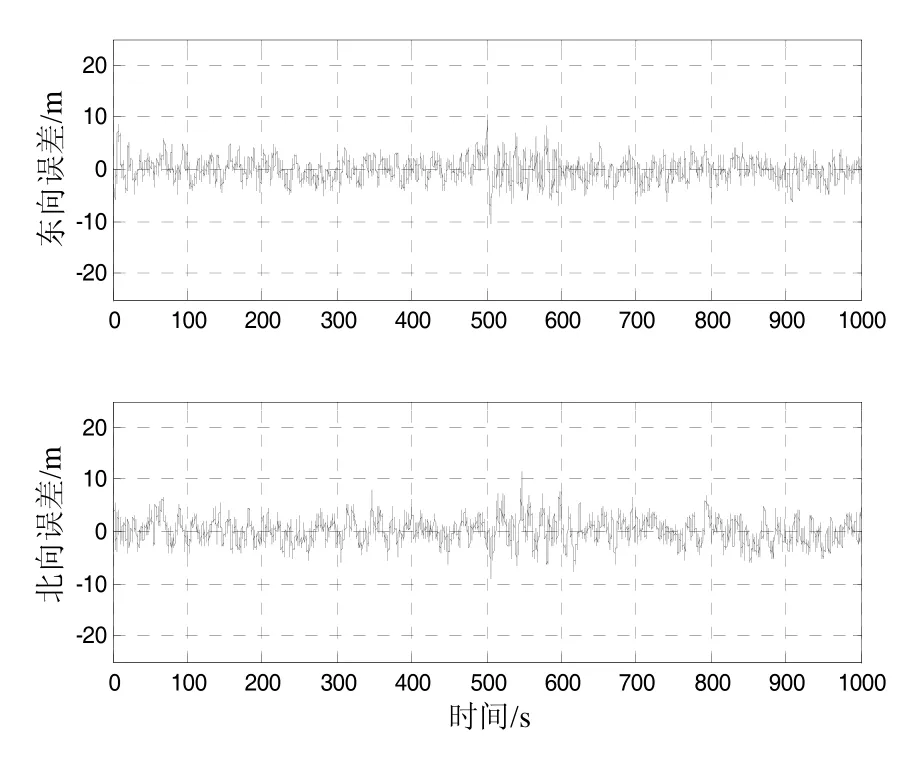
图6 带多重次优渐消因子的ISTUKF定位误差Fig.6 Position error of ISTUKF with multiple suboptimal fading factor
标准UKF与提出的ISTUKF得到的东向、北向位置误差如图4~6所示。可以看到,在系统正常状态下,标准UKF与提出的ISTUKF均可实现飞机的准确定位。当在500~600 s时间段引入状态突变量后,标准UKF定位误差急剧增大,在该时间段内,标准 UKF得到的东向、北向位置误差在[9.3 m, 23.5 m]内。提出的ISTUKF由于能够快速检测出状态异常并实时调整滤波增益矩阵,得到的定位精度相比标准UKF明显提高,在 500~600 s时间段,带单重次优渐消因子的ISTUKF得到的东向、北向位置误差在[-13.7 m, 14.9 m]内;带多重次优渐消因子的ISTUKF得到的东向、北向位置误差在[-10.0 m, 12.1 m]内。与带单重次优渐消因子的ISTUKF相比,带多重次优渐消因子的ISTUKF由于对不同的状态分量以不同的速率调节,因而得到的定位精度更高。
表1给出了标准UKF与ISTUKF在500~600 s时间段内东向、北向位置误差的平均误差(mean error)与均方根误差(root mean square error, RMSE)。由表1可以看出,提出的ISTUKF的平均误差与均方根误差均明显小于标准UKF,表明当系统状态存在异常时,提出的ISTUKF滤波算法可以有效地提高滤波精度,减小INS/GPS组合导航系统的定位误差。
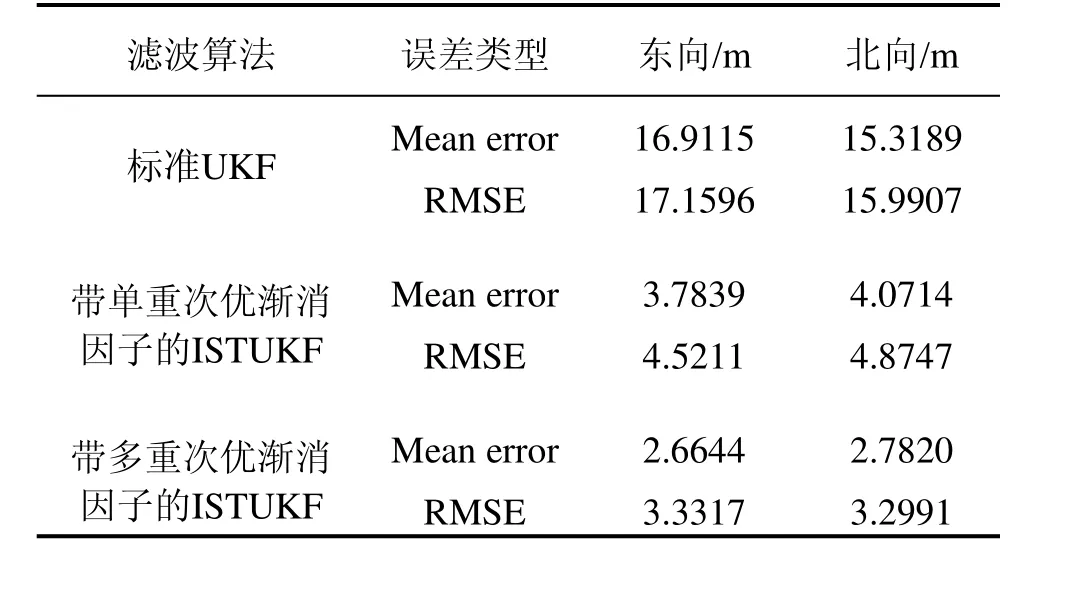
表1 INS/GPS组合导航系统误差比较Tab.1 Error comparison for the INS/GPS integration
4 结 论
本文提出一种改进的强跟踪UKF滤波算法以克服标准UKF在系统状态异常时滤波精度降低的缺陷。该算法采用假设检验的方法对异常状态进行检测,当系统状态出现异常时,通过对预测协方差阵引入次优渐消因子来自适应地调整滤波增益,进而实现滤波算法对系统真实状态的强跟踪。该算法中次优渐消因子的确定无需计算系统模型的雅克比矩阵,提高了传统强跟踪UKF的实用性。提出的强跟踪UKF具有两种形式:带单重次优渐消因子与带多重次优渐消因子。将提出的算法应用于INS/GPS组合导航系统进行仿真验证,并与标准UKF进行比较,结果表明,在系统状态存在异常时,提出的强跟踪UKF可以有效地检测出异常状态并自适应调节滤波增益,滤波性能明显优于标准UKF,提高了INS/GPS组合导航系统的定位精度。
(
):
[1] Groves P D. Principles of GNSS, inertial, and multisensor integrated navigation systems[M]. London, Boston: Artech House, 2008.
[2] 杨波,秦永元,柴艳. UKF 在 INS/GPS 直接法卡尔曼滤波中的应用[J]. 传感技术学报,2007,20(4):842-846.
YANG Bo, QIN Yong-yuan, CHAI Yan. Application of UKF in direct method of Kalman filter for INS/GPS[J]. Chinese Journal of Sensors and Actuators, 2007, 20(4): 842-846.
[3] Ali J, Mirza M R U B. Performance comparison among some nonlinear filters for a low cost SINS/GPS integrated solution[J]. Nonlinear Dynamics, 2010, 61(3): 491-502.
[4] Xiong K, Zhang H Y, Chan C W. Performance evaluation of UKF-based nonlinear filtering[J]. Automatica, 2006, 42(2): 261-270.
[5] 薛丽,高社生,胡高歌. 自适应 Sage-Husa 粒子滤波及其在组合导航中的应用[J]. 中国惯性技术学报,2013,21(1):84-88.
XUE Li, GAO She-sheng, HU Gao-ge. Adaptive Sage-Husa particle filtering and its application in integrated navigation[J]. Journal of Chinese Inertial Technology, 2013, 21(1): 84-88.
[6] Gao S S, Hu G G, Zhong Y M. Windowing and random weighting-based adaptive unscented Kalman filter[J]. International Journal of Adaptive Control and Signal Processing, 2014 (in press).
[7] 周东华,席裕庚,张钟俊. 一种带多重次优渐消因子的扩展卡尔曼滤波器[J]. 自动化学报,1991,17(6): 689-695.
ZHOU Dong-hua, XI Yu-geng, ZHANG Zhong-jun. A suboptimal multiple fading extended Kalman filter[J]. Acta Automatica Sinica, 1991, 17(6): 689-695.
[8] 杨文博,李少远. 基于强跟踪UKF的航天器自主导航间接量测滤波算法[J]. 系统工程与电子技术,2011,33(11):2485-2491.
YANG Wen-bo, LI Shao-yuan. Autonomous navigation filtering algorithm for spacecraft based on strong tracking UKF[J]. Systems Engineering and Electronics, 2011, 33(11): 2485-2491.
[9] Zhang Z T, Zhang J S. A strong tracking nonlinear robust filter for eye tracking[J]. Journal of Control Theory and Applications, 2010, 8(4): 503-508.
[10] 钱华明,黄蔚,孙龙,等. 基于多重次渐消因子的强跟踪 UKF姿态估计[J]. 系统工程与电子技术,2013,35(3):580-585.
QIAN Hua-ming, HUANG Wei, SUN Long, et al. Attitude estimation of strong tracking UKF based on multiple fading factors[J]. Systems Engineering and Electronics, 2013, 35(3): 580-585.
Improved strong tracking UKF and its application in INS/GPS integrated navigation
HU Gao-ge, LIU Yi-han, GAO She-sheng, YANG Yi
(School of Automatics, Northwestern Polytechnical University, Xi’an 710072, China)
The performance of the standard UKF would be degraded when the system states are abnormal due to the absence of capability to adapt itself to the changing conditions. This paper presents an improved strong tracking UKF (ISTUKF) to overcome the limitation of the standard UKF. The hypothesis testing method is employed in the ISTUKF to identify the abnormal system states, and in case they occur, the suboptimal fading factors are introduced into the prediction covariance to adaptively adjust the Kalman gain matrix to realize the strong tracking of the real state. Compared with the traditional strong tracking UKF, the proposed ISTUKF avoids the cumbersome evaluation of Jacobian matrices involved in the calculation of the suboptimal fading factors, making it more applicable. The proposed ISTUKF is applied to the INS/GPS integrated system for simulation in comparison with the standard UKF. The simulation results demonstrate that the position errors in east and north obtained by the ISTUKF with single suboptimal fading factor are within [-13.7 m, 14.9 m], and the corresponding errors obtained by the ISTUKF with multiple suboptimal fading factors are within [-10.0 m, 12.1 m]. The performance of the proposed ISTUKF is significantly superior to that of the standard UKF, leading to improved position precision.
strong tracking filter; unscented Kalman filter; suboptimal fading factor; INS/GPS integrated navigation
联 系 人:高社生(1956—),男,教授,博士生导师,研究方向为导航、制导与控制。E-mail:gshshnpu@163.com
1005-6734(2014)05-0634-05
10.13695/j.cnki.12-1222/o3.2014.05.015
U666.1
A
2014-05-20;
2014-09-04
国家自然科学基金(基金号61174193);西北工业大学博士论文创新基金(项目号CX201409)
胡高歌(1988—),男,博士研究生,从事组合导航与非线性滤波算法研究。E-mail:hugaoge1111@126.com
