基于克里格重构的区域地磁变化场短时预测模型

牛 超，刘代志，王跃钢，李夕海，杨晓君

（第二炮兵工程大学，西安 710025）

基于克里格重构的区域地磁变化场短时预测模型

牛 超，刘代志，王跃钢，李夕海，杨晓君

（第二炮兵工程大学，西安 710025）

区域地磁变化场建模与预测是地磁辅助导航、空间环境监测与预报等领域的重要研究课题。结合时域上的单台站地磁变化场预测，以及空间域上的区域地磁变化场重构，提出了一种基于克里格重构的区域地磁变化场短时预测模型。以区域范围（101°E~111°E，30°N~40°N）的地磁测站2009年的数据为实例，结果表明：1）基于克里格方法重构的区域地磁变化场 Z分量，准确合理的反映了其时空变化特性；2）在短时预测中，区域模型能紧跟地磁变化场的变化趋势，说明其能很好地描述变化磁场的时空演化特性，且位于区域边缘的台站预测误差稍大。当预测期为1 h、6 h、12 h、24 h时，区域地磁变化场预测模型的平均绝对误差分别为1.67 nT、2.19 nT、2.72 nT、3.14 nT。

克里格重构；区域地磁变化场；预测模型；地磁导航

地磁导航是利用地球稳定磁场（包括主磁场和局部磁异常场）进行匹配制导的一种新型导航方法[1-2]。变化磁场虽然只占地球总磁场的 1%左右，但是对地磁导航的影响巨大，一般来说，其日变幅高达几十纳特[3]。文献[4]亦指出在我国某区域，地磁分量值每千米的最大变化量也不过3.6 nT。而目前普通的地磁匹配基准图只能反映地球稳定磁场，无法对地球变化磁场做出自适应的修正。因此，区域地磁变化场的分析和建模研究很重要，并且其在应用地磁学研究的许多领域都有作用体现，如高精度陆地、海洋磁力测量中的日变改正；震磁效应研究等。

变化磁场建模不同于稳定磁场。稳定磁场中的地壳磁异常场其空间分布复杂但时间演化上较稳定。小至一块磁性岩石，大至整个地壳，都有其特有的磁场分布，因此，要建立稳定磁场模型，需要大量的空间采样点。而地球变化磁场虽然也具有复杂的空间分布与时间演化，但其规律性也较明显，一个地磁观测站能够以一定精度表达一片区域的变化磁场，如果利用区域内多个地磁测站，则能以更高精度表达较大区域的变化磁场，循此规律性利用现代智能信号处理方法辅以地统计学理论，就可对其做出较高精度的预测。因此，本文结合时域上的单台站地磁变化场预测，以及空间域上的区域地磁变化场克里格重构，提出了一种基于克里格重构的区域地磁变化场预测模型。

1 基于改进克里格法的区域地磁变化场重构及精度评估

1.1 区域地磁变化场的克里格重构理论

克里格法是由Krige提出的一种地统计学方法。已有学者基于克里格法进行了电离层相关参数（如电离层TEC、f0F2）的区域重构问题研究[5-8]，并取得了较好的效果。

将克里格法用于地磁变化场区域重构，设 B(x,y)为地磁变化场的某个地磁分量，已知区域内n个地磁台站的地磁变化场某地磁分量值 B(xi,xj)，其中 i= 1,2,…, n，则区域内任一点 (x0,y0)的克里格估计量 Bp(x0,y0)可表示为：

式中， Wi为权重系数。Benkova[9]指出，在一定空间范围内，地磁变化场的差异性在经度和纬度方向上是不同的，纬度效应较经度效应更大些，两者大概差一个量级。因此，这里对算法中的空间距离进行了改进，以将克里格法用于地磁变化场区域重构。对于空间两点 Pi和 Pj，引入地磁变化场距离d，则 Pi和 Pj的之间距离 dij定义为：

式中，Lon(i)和Lat(i)分别为i点的经度和纬度；ε为尺度因子，以考虑地磁变化场随空间的分布在经向和纬向的区别，这里选取 ε= 10。

变异函数采用通过原点的线性型：

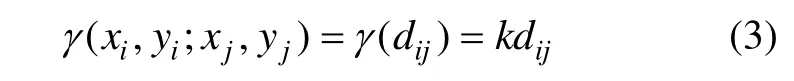
可得到用于地磁变化场区域重构的克里格方程组：

该方程组与变异函数的斜率无关，及线性模型的斜率并不影响重构的结果。

1.2 重构精度评估

地磁变化场的重构精度用交叉验证法（Cross validation）来衡量。计算重构值 ZEstimation和实测值ZMeasure之差的均方根值σ(称为重构误差)，并作为评估重构方法优劣的标准：

式中，N为参加评估的样本数。

2 区域地磁变化场重构实例

2.1 数据基础

我国有着分布合理的国家地磁台网和区域地磁测阵。这些地磁台站能够提供比较准确的地磁分量值，对于区域地磁变化场的分析与建模有很大帮助。图 1为所选区域（101°E～111°E，30°N～40°N）的地磁测站位置示意图。

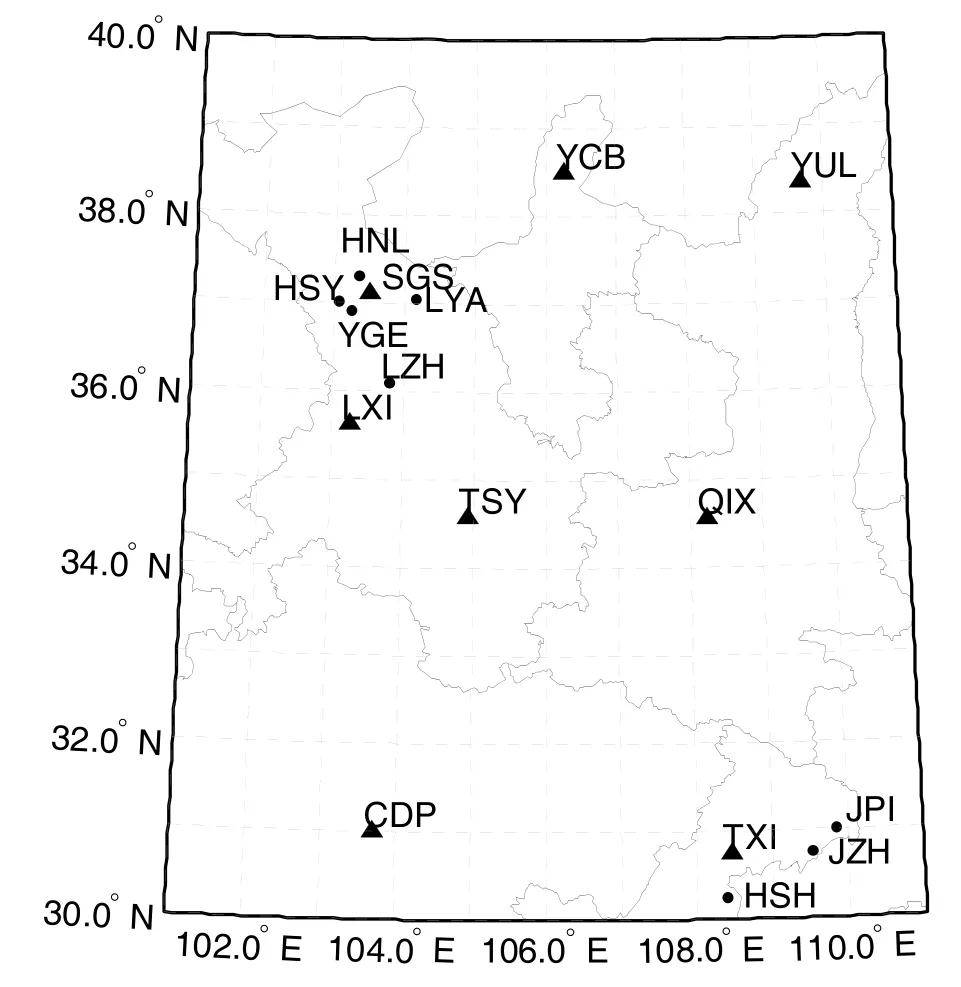
图1 区域地磁测站的位置示意图Fig.1 Location map of the geomagnetic observatory in regional area

由于Z分量是地磁辅助导航中地磁场建模与预测的优良匹配分量[10]，因此，本文选择地磁场Z分量进行区域重构及建模分析。

2.2 重构实例

在该区域内，选取了8个地磁台站（榆林YUL、天水TSY、乾陵QIX、银川YCB、天星TXI、临夏LXI、松山SGS、成都CDP，台站位置见图1中三角形所示）的2009年实测数据，基于改进克里格法，进行区域地磁变化场重构。

地磁变化场Z分量在时间上的演化规律主要随地方时变化。午夜时段（0200LT）曲线较为平缓，在太阳升起前一段时间（一般到0800LT），地磁Z分量逐渐增大，此后，随后随着太阳高度角的逐渐增大，地磁Z分量逐渐减小，一直到正午（1200LT左右），此时，地磁Z分量达到最低点，之后地磁Z分量开始逐渐增大，一直到日落（2000LT），地磁Z分量趋于平缓。如图2所示。

因此，这里选取了四个典型时刻（0800LT（日出）、1200LT（午后）、2000LT（日落）、0200LT（午夜））进行地磁Z分量的重构。图3给出了该区域2009年8月18日0800LT（日出）、1200LT（正午）、2000LT（日落）、2009年8月19日0200LT（午夜）的四幅实测地磁变化场Z分量重构图。根据该区域内8个地磁台站实测地磁变化场Z分量值，以30＇×30＇为网格，重构了该区域的地磁变化场Z分量等值线图。图中三角形代表地磁台站位置，临近的数字代表相应时刻的实测地磁变化场Z分量值，等值线上的数字代表等值线对应的值。

图 3(a)为 2009.8. 18日出（0800LT）的重构图像，由于太阳从东方升起，所以从图 3(a)可以看出等值线上的数值从东向西递增，东西向梯度较显著；图3(b)为2009. 8.18正午（1200LT）的重构图像，由于太阳高度角比较大，地磁变化场Z分量绝对值整体较大，且等值线从北向南逐渐增大，梯度变化也较大，在 25°N 附近达到最大值，这反映了它正处于北半球Sq电流涡焦点处；图3(c)(d)分别为2009.8.18日落（2000LT）和2009.8.19午夜（0200LT）的重构图像，此时已处于夜晚，所以等值线数值较小。可见，用Kriging方法重构区域范围的地磁变化场Z分量，以三维的形式（时间，纬度，经度）展示了地磁变化场Z分量的变化，合理的反映了其时空变化特性，所以可以预期把该方法应用于区域地磁变化场Z分量的现报和预报中。

图2 地磁变化场Z分量日变化曲线（成都台站2009.8.13LT0000:2400）Fig. 2 Diurnal curve of geomagnetic Z component (CDP observatory 2009.8.13LT0000:2400)

图3 地磁变化场Z分量四个典型时刻重构等值线分布图：(a) 0800LT日出；(b) 1200LT正午；(c) 2000LT日落；(d) 0200LT午夜Fig. 3 Reconstruction contour maps of geomagnetic Z component at four typical time: (a) 0800LT Sunrise; (b) 1200LT Noon; (c) 2000LT Sunset; (d) 0200LT Midnight

2.3 重构误差分析

为了评估地磁变化场Z分量重构的准确性和合理性，对其重构误差进行了统计。因地磁变化场具有明显的劳埃德（Lloyd）季节变化，3、4、9、10月为分点月份，用E表示，5、6、7、8月为夏至点月份，用J表示，11、12、1、2月为冬至点月份，用D表示，且每天的地磁活动情况均不同，所以为了更全面地说明地磁变化场Z分量的区域重构效果，表1~3分别给出了该区域2009年8月份四个典型时刻、2009年三个不同劳埃德月份，以及不同地磁活动水平的平均重构误差结果。

对结果进行分析发现：地磁场本身的变化、地磁活动水平和台站布局是区域重构误差的主要来源。对于第一个因素，根据地磁变化场的日变特性，午夜Z分量的数值较小，且变化比较稳定，因此重构误差较小，而在正午时，磁层——电离层电流体系强度较大，Z分量绝对值较大，此时的重构误差就大些，这由表1结果可以直观看出。对于第二个因素，不同的地磁活动水平影响着区域地磁变化场的重构精度，从长时间范围看，主要体现在不同的劳埃德季节方面，地磁夏至点月份（J）误差较大，其次为地磁分点月份（E），地磁冬至点月份误差最小（D），其根源为日地距离不同引起的辐射不同，这由表2可以直观看出。从短时间范围来看，重构误差正比于地磁活动水平，地磁活动较剧烈时，重构误差较大，比如发生大的地磁扰动，甚至磁暴，从表3可以直观看出。对于第三个因素，从表1-3均可以看出，若一个台站其周围有多个台站，且形成包围布局，比如天水TSY和乾陵QIX，该台站的重构误差就比较小；反之，若台站处于区域边缘，则误差较大。

表1 区域地磁变化场Z分量重构误差（2009年8月四个典型时刻）Tab.1 Reconstruction error of regional geomagnetic Z component (four typical times in 2009.8) unit: nT

表2 区域地磁变化场Z分量平均重构误差（不同劳埃德季节）Tab.2 Reconstruction error of regional geomagnetic Z component (different geomagnetic Lloyd seasons) unit: nT

表3 区域地磁变化场Z分量平均重构误差（不同地磁活动水平）Tab.3 Reconstruction error of regional geomagnetic Z component (different geomagnetic activity levels) unit: nT

3 基于克里格重构的区域地磁变化场预测模型

3.1 建模步骤

前期已做了单站地磁变化场的 MEEMD-样本熵-LSSVM预测模型相关研究，这里将时域上的单站地磁变化场Z分量预测，和地域上的区域地磁变化场重构相结合，以进行区域地磁变化场的短时预测。利用地磁台站的实测地磁变化场数据，给出区域范围的预测等值线，并对该方法的预测精度进行评估。

预测任务：区域范围内任一地点地磁变化场的短时预测值（提前1~24 h预测）。

具体步骤：

1）数据处理：将区域内所有地磁台站的变化磁场Z分量序列最小时间尺度划归到10 min，形成各台站10 min均值的地磁变化场Z分量序列；

2）单站预测：对区域内的每个地磁台站，采用MEEMD-样本熵-LSSVM预测模型，预测各个站提前1~24 h的地磁变化场Z分量值，评估单站预测精度；

3）区域重构及预测：对区域内N个地磁台站某一时刻的地磁变化场Z分量预测值进行区域重构，即可求得区域内任一地点地磁变化场Z分量预测值，给出提前 1 ~24 h的预测等值线，评估其预测误差。

3.2 短时预测实例

首先进行单站预测。用2009.8.13LT0800LT至8.18LT0800T共5天的数据做模型训练，用2009.8.18LT0800至2009.8.19LT0800共1天的数据做模型预测检验，分别做提前1 h、6 h、12 h、24 h的单站预测。在此基础上，对区域内 8个地磁台站某一时刻的预测值，进行区域重构。图4(a)(c)(e)(g)分别为提前1 h、6 h、12 h、24 h预测的等值线分布图，网格为30＇×30＇，图 4(b)(d)(f)(h)为对应时刻根据实测值重构的等值线分布图。提前 1 h预测的时刻为2009.8.18LT1200，提前 6 h预测的时刻为2009.8.18LT1400LT，提前12 h预测的时刻为2009.8.18LT2000，提前24 h预测的时刻为2009.8.19LT0800。

从图4(a)(b)(c)(d)可以看出，根据预测值以及实测值重构的等值线图，其形状、大小及尺度很相似，这说明了本文提出的预测方法在提前1 h和6 h预测情况下是可以实施的并达到了一定的精度，预测结果比较准确的反映地磁变化场的时空变化特性，但从图4(e)(f)(g)(h)可以看出，根据预测值重构的等值线图与根据实际观测值重构的等值线图差异性较大，说明随着预测时长的增大，预测难度增大。

图4 根据预测值和实测值重构的等值线分布图，(a)(c)(e)(g)分别为提前预测1 h、6 h、12 h、24 h等值线分布图，(b)(d)(f)(h)分别为对应时刻的根据实测值重构的等值线分布图Fig. 4 Reconstruction contour map of forecasting value and observed value, (a)(c)(e)(g) respectively represent the contour map for 1 h, 6 h, 12 h, 24 h ahead predictions, (b)(d)(f) (h) respectively represent the contour map of observed value for the corresponding time

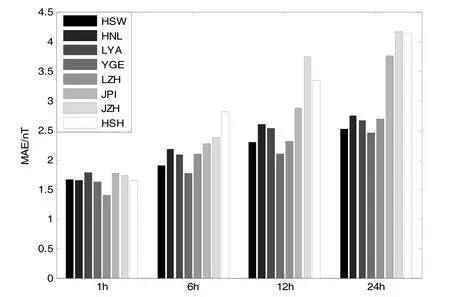
图5 区域内检验台站预测期分别1 h、6 h、12 h、24 h的平均绝对误差Fig. 5 Mean absolute errors for forecasting period 1 h, 6 h, 12 h, 24 h of test geomagnetic observatory

图6 区域内检验台站预测结果Fig. 6 Forecasting results of test geomagnetic observatory

3.3 区域预测精度评估

基于区域内其它几个检验地磁台站(图 1中圆点所示台站)进行精度评估，采用平均绝对误差(Mean Absolute Error，MAE)作为预测评价函数。在所选区域内获取数据的台站还有：红沙湾(HSW）、横梁(HNL)、芦阳(LYA)、莺歌(YGE)、兰州(LZH)、建坪(JPI)、荆竹(JZH)、黄水(HSH)，用这些台站的数据分别做预测期为1 h、6 h、12 h、24 h的检验。图5为区域内各检验台站预测期为1h、6 h、12 h、24 h的平均绝对误差。图6为检验台站预测期分别为1 h、24 h的预测结果示意图。

4 结 论

本文讨论了一种基于克里格重构的区域地磁变化场预测模型，以区域范围（101°E~111°E，30°N~ 40°N）的地磁测站2009年的数据为实例，结果表明：1）基于克里格方法重构的区域地磁变化场Z分量，准确合理地反映了其时空变化特性；2）在短时预测中，重构预测模型能紧跟地磁变化场的变化趋势，说明其能很好地描述变化磁场的时空演化特性。本文为实现区域地磁变化场短时高精度预测提供了新的思路，对于更好地推动地磁辅助导航等军事工程应用有一定的意义。

（References）：

[1] 朱占龙，杨功流，单友东，等. 一种关于地磁图适配型分析的综合评价方法[J]. 中国惯性技术学报，2013，21(3)：375-380.

ZHU Zhan-long, YANG Gong-liu, SHAN Youdong, et al. Comprehensive evaluation method of geomagnetic map suitability analysis[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 375-380.

[2] 王仕成，刘元元，孙渊，等. 基于 Legendre函数的超高阶地磁场建模方法[J]. 中国惯性技术学报，2012，20(3)：333-338.

WANG Shi-cheng, LIU Yuan-yuan, SUN Yuan, et al. Method for ultra highorder magnetic model based on Legendre function[J]. Journal of Chinese Inertial Technology, 2012, 20(3): 333-338.

[3] 李军辉，李琪，王行舟，等.中国大陆地磁场Z分量日变幅的时空特征分析[J]. 中国地震，2012，28(1)：42-50.

LI Jun-hui, LI Qi, WANG Xing-zhou, et al. Spatial and temporal variation of geomagnetic vertical daily ranges in Chinese mainland[J]. Earthquake Research in China, 2012, 28(1): 42-50.

[4] 陈励华，王仕成，孙渊，等. 地磁缓变区域的多维特征量匹配方法[J]. 中国惯性技术学报，2011，19(6)：720-724.

CHEN Li-hua, WANG Shi-cheng, SUN Yuan, et al. Matching of multi-dimensional feature elements in areas with smooth magnetic fields[J]. Journal of Chinese Inertial Technology, 2011, 19(6): 720-724.

[5] Sparks L, Blanch J, Pandya N. Estimating ionospheric delay using kriging: 1. Methodology[J]. Radio Science, 2011, DOI: 10.1029/2011RS004667.

[6] Foster M P, Evans A N. An evaluation of inter- polation techniques for reconstructing ionospheric TEC Maps[J]. Geoscience and Remote Sensing, 2008, 46(7): 2153-2164.

[7] Wang R, Zhou C, Deng Z, et al. Predicting foF2 in the China region using the neural networks improved by the genetic algorithm[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2013, 92: 7-17.

[8] Habarulema J B, Mckinnell L A. Investigating the performance of neural network backpropagation algorithms for TEC estimations using South African GPS data [J]. Ann. Geophys., 2012, 30: 857-866.

[9] Benkova N P. Spherical harmonic analysis of the Sq variations[J]. Terr. Mag. Atomos. Elect, 1940, 45, 425.

[10] 齐玮，王秀芳，李夕海，等. 基于统计建模的地磁匹配特征量选择[J]. 地球物理学进展，2010，25(1)：324-330.

QI Wei, WANG Xiu-fang, LI Xi-hai, et al. Selection of characteristic components for geomagnetic matching based on statistical modeling[J]. Progress in Geophysics, 2010, 25(1): 324-330.

Regional geomagnetic short-term forecasting model based on Kriging reconstruction method

NIU Chao, LIU Dai-zhi, WANG Yue-gang, LI Xi-hai, YANG Xiao-jun
(The Second Artillery Engineering University, Xi’an 710025, China)

The modeling and forecasting of regional geomagnetic variation field is an important research topic of geomagnetic navigation and space environment monitoring. Combining the time-domain forecasting of the single geomagnetic observatory and the space-domain reconstruction of the regional geomagnetic variation field, this paper proposes a regional geomagnetic forecasting model based on Kriging reconstruction method. It shows that: 1) the regional geomagnetic Z component reconstructed by Kriging method can reasonably and accurately reflect its spatial-temporal variation characteristics; 2) the regional model can closely keep up with the trend of geomagnetic variation field in short-term forecasting, which indicates that the model can accurately describe the spatial-temporal evolution characteristics. The forecasting errors of geomagnetic observatory located in the area edge are larger. When the forecasting period is 1 h, 6 h, 12 h, 24 h, the mean absolute error of the regional model is 1.67 nT, 2.19 nT, 2.72 nT and 3.14 nT, respectively.

Kriging reconstruction; regional geomagnetic variation field; forecasting model; geomagnetic navigation

牛超 （1986—），男，博士，工程师，从事地磁导航、地磁信息处理等理论与方法研究。E-mail：niuchao0511@163.com

1005-6734(2014)04-0492-06

10.13695/j.cnki.12-1222/o3.2014.04.013

P318.2

A

2014-02-27；

2014-05-30

国家自然科学基金资助项目（41374154，61304240）