基于速度阻尼的双轴旋转式激光陀螺捷联惯导标定方法

王 彬，翁海娜，汪湛清，张宇飞，胡小毛

（1. 天津大学 机械工程学院，天津 300072；2. 天津航海仪器研究所，天津 300131；3. 北京理工大学 自动化学院，北京 100081）

基于速度阻尼的双轴旋转式激光陀螺捷联惯导标定方法

王 彬1，翁海娜2，汪湛清3，张宇飞2，胡小毛2

（1. 天津大学 机械工程学院，天津 300072；2. 天津航海仪器研究所，天津 300131；3. 北京理工大学 自动化学院，北京 100081）

惯性元件参数的长期稳定决定着惯导系统的精度，目前对于激光陀螺捷联惯导系统（RLG-SINS）主要是采用系统级旋转调制技术来实现高精度导航能力，同时系统级旋转也提高了初始对准精度以及惯性元件误差的可观测性。针对激光陀螺惯导系统惯性元件误差项的特点，同时结合分立式标定与系统级标定各自的优势，设计了一种水平阻尼模式下的 Kalman滤波方案，利用双轴旋转机构，通过观测导航位置误差来实现初始对准以及部分惯性元件误差参数的标定，可以有效地减小惯性元件逐次启动误差对导航精度的影响。仿真结果表明，系泊状态零速度阻尼模式下工作4 h，可以标定出石英加速度计标度因数误差、零偏与激光陀螺零偏，共计9项误差参数。加速度计零偏估计误差小于2%，陀螺零偏估计误差小于8%，误差估计精度满足高精度惯性导航要求，该方法具备一定的工程实用性。

速度阻尼；双轴旋转调制；系统级标定；系泊状态

惯性导航系统可以不间断提供载体全部的运动参量(姿态、速度、位置等)，对外既不吸收能量也不辐射能量，同时具有较强的隐蔽性、抗干扰能力以及较高的信息输出精度。为了满足高精度惯性导航的需求，目前主要采用系统级旋转调制技术[1-2]，它可以有效地降低研制高精度惯性元件所带来的高昂费用，本质是通过旋转改变惯性元件慢变漂移的传播特性，抑制其在导航误差中的积累。此外，惯性导航系统属于积分推算过程，初始对准和惯性元件误差的标定过程也直接或间接影响着导航定位精度，由于初始速度、位置信息可以通过其他设备精确测得，只需着重考虑初始姿态信息的获取。文献[3]借助了旋转式系统框架的旋转，通过绕垂向轴往复旋转，调制了水平惯性元件的输出误差，可以有效提高初始对准的精度和时间。通过转位机构，还可以有效激发惯性元件误差可观测性，实现标定过程，因此旋转可以实现初始对准、惯性元件误差标定与导航输出三方面精度的共同提升。

激光陀螺惯性测量组件(IMU)的精确标定是实现高精度导航的重要前提，目前，按照观测量的不同，标定分为两种——分立式标定和系统级标定[4-6]。分立式标定法主要借助实验室环境下高精度的三轴转台，由于高精度转台的回转误差和不垂直度很小，惯性元件的标定极限精度可以达到转台的误差精度，但不能克服逐次启动误差；系统级标定降低了转台精度限制，只需要低精度的转位机构即可完成惯性元件的标定，但需要设定专门的误差激励路径，会存在状态量过多、可观性复杂所导致的误差项激励不彻底的情况。因此本文针对激光陀螺惯性测量组件的误差特性，结合两种标定方法的各自优势，借助双轴旋转机构，在系泊状态下采用水平阻尼工作模式[7-8]，设计一种适用于工程实践的惯性元件系统标定和初始对准方案，同时进行了数学仿真，验证了该方案的可行性。

1 双轴旋转惯导系统初始对准与标定方法

1.1 初始对准方法

首先定义下文所用到的正交坐标系：n系为东北天导航坐标系；b系为右艏上载体坐标系；e系为地球坐标系，与地球相固联；i 系为惯性坐标系；p系为旋转坐标系，即惯性元件安装的坐标系。由于捷联式惯导系统需要建立数学平台，初始对准最重要的任务是得到载体(或惯组)坐标系相对于导航坐标系的姿态变换矩阵，主要是通过粗对准和精对准两个过程实现，其中失准角估计的极限精度表示为如下公式[9-10]：

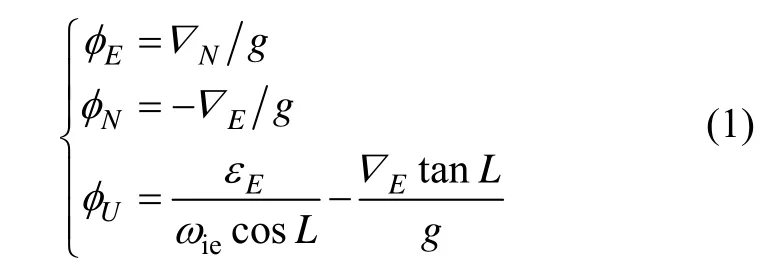
通过式(1)可以得出，姿态对准的精度大都与水平惯性元件误差有关，由于海浪属于周期性摇摆，横纵摇摆平衡位置也近似水平，通过绕垂向轴旋转可以使绝大部分的水平惯性元件误差调制成周期性变化，间接改变了惯性元件慢变漂移在导航坐标系的传播途径，使得▽N、▽E和 εE在一个旋转周期内对惯导系统的影响降低到最小。同时，姿态对准过程与惯性元件误差标定过程是紧密联系的，高精度的姿态对准也保证了高精度的元件误差标定。

1.2 标定方法

惯性测量组件在出厂之前首先是在实验室条件下的高精度三轴转台标定，惯性元件的安装误差可以得到精确的标定，具有较高的长期稳定性，同时激光陀螺的标度因数也非常稳定[9]，但是石英加速度计标度因数误差、零偏和激光陀螺零偏容易受到环境变化因素影响，具有逐次启动误差，但是这些误差项大都具有较高的一次通电稳定性。针对这一问题，设计一种系统级标定方案，用来标定这9项惯性元件的误差参数。采取一次通电标定误差后对惯导系统进行反馈校正，然后直接转入导航模式，以提高惯导系统导航精度。

通过绕垂向轴旋转可以在保证初始姿态对准精度的同时，也可以有效地提高了与转轴相垂直的惯性元件误差的可观测性[3]，尤其是水平加速度计零偏可以在较短的时间内得到较高的估计精度。同时由于惯导系统等效北向陀螺零偏可观测，因此可通过捷联姿态矩阵，转换为水平陀螺零偏的估计。基于此方法，对上述9个误差项进行估计和补偿，惯性元件误差如下：

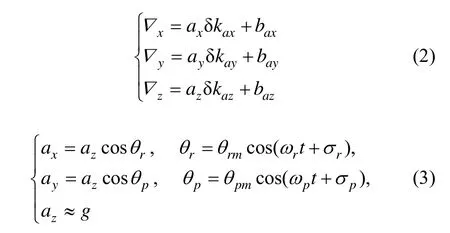
式中：▽i、δkai和bai(i = x,y,z)为石英加速度计总的测量误差、标度因数误差和零偏， ai(i = x,y,z)为三轴加速度计测量输出，θr和 θp表示海浪横摇和纵摇变量，θrm、ωr、σr和 θpm、ωp、σp分别表示为横纵摇摆幅度、频率和初相位。在海浪周期性摇摆状态下，垂向加速度 az通过姿态分解传递给水平加速度计 ax和ay，耦合标度因素误差δkax和δkay后，叠加零偏 bax和bay造成水平加速度计总的测量误差▽x和▽y；同时可以看出，由于 ax和 ay是时变的，因此可以从▽i中分离出δkai和 bai。系泊状态下位置固定，由于载体存在三个自由度的振荡性线运动（横移、纵移和升沉），虽然幅度很小，也会使惯导产生微小的运动加速度；同时也存在未完全补偿掉的杆臂误差、尺寸效应耦合海浪摇摆所产生运动加速度，如果选用导航输出的速度误差作为滤波器观测量将会带来估计误差，所以选取导航输出的位置误差作为观测量。通过可观测性分析可知，这9项惯性元件误差在一定的双轴旋转条件下均是可以观测估计的[4,11]。

2 水平阻尼工作模式下惯导的误差方程

2.1 水平阻尼方法引入

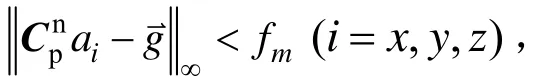
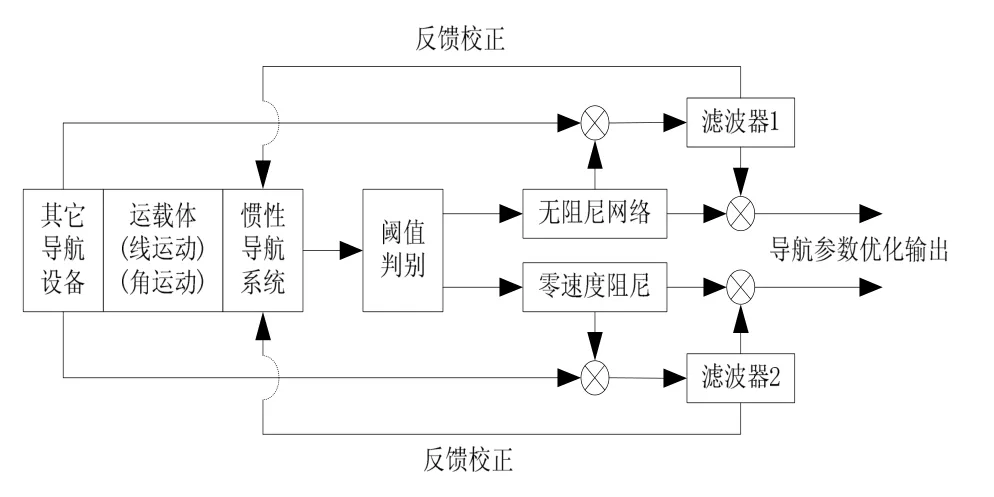
图1 水平阻尼模式下Kalman滤波框图Fig.1 Block diagram of Kalman filter in level-damp mode

2.2 阻尼条件下的惯导误差方程

在水平阻尼条件下构建惯性元件9项误差参数滤波器系统模型，由于系泊状态下位置已知，状态选为姿态误差(φ)、速度误差(δv)、位置误差(δp)、加速度计标度因数误差(δka)、加速度计零偏(ba)、陀螺零偏(ε)以及阻尼网络中间变量(ℓ)，共 20维，则滤波器系统方程和观测方程表示为：

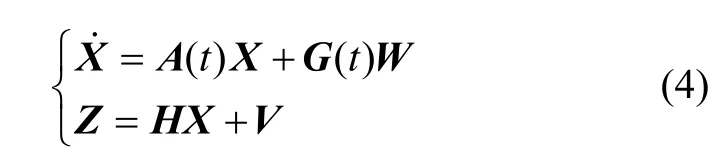
式中：X=[φ δvδpδkabaε ℓ]T，A( t)、G(t)分别为时变的状态矩阵和系统噪声矩阵，观测量Z选为位置误差，H为观测矩阵，系统噪声W和观测噪声V服从正态分布的高斯白噪声，系统方程和观测方程详细的数学描述可参见文献[9]。由于惯导系统近似为低通系统，仿真过程中，考虑到误差方程的简化、运算维数的降低，水平阻尼网络采用一阶形式，同时两水平通道采用相同的阻尼网络，如下所示：

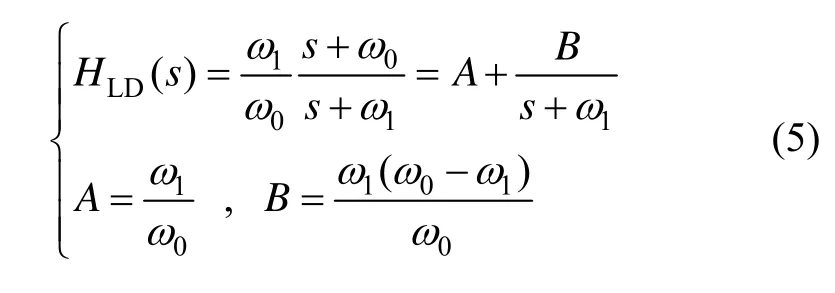
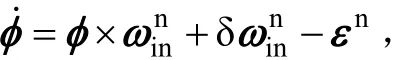
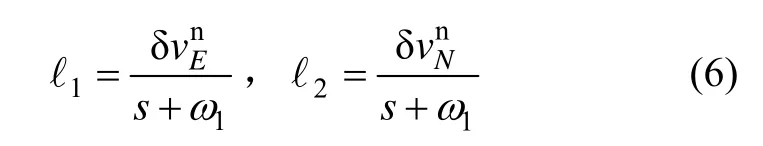
考虑到采用闭环Kalman滤波估计之前已经完成了粗对准，不考虑大失准角影响，从而保证了误差方程的线性化，则水平阻尼模式下的惯导误差方程可以表示为公式(7)形式：

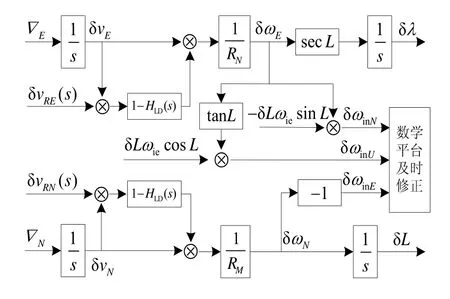
图2 水平阻尼模式下惯导系统误差简化框图Fig.2 Simplified block diagram of INS error in level-damp mode

3 仿真验证

3.1 仿真条件设置

为进一步验证系泊状态下水平阻尼滤波器算法的有效性，下面利用仿真数据进行处理分析，需要说明的是，仿真实验是建立在粗对准已经完成基础之上的，仿真实验参数设定值如表1所示。

表1 仿真实验参数设定值Tab.1 Parameter setting of digital simulation

将上述噪声项与海浪摇摆共同叠加至惯性元件生成的原始数据中，惯导系统采用单子样算法，解算频率为400 Hz，测试地点位置信息固定已知，利用水平阻尼方案，结合Kalman滤波器对惯性元件的9项误差参数和初始姿态角度进行估计，并与参考值对比，位置1是初始位置，整个旋转过程分为以下步骤进行：

步骤1：绕 zb轴正反两位置转停2 h；

步骤2：绕 yb轴正向旋转90°到达位置3；

步骤3：绕 zb轴正反两位置转停2 h；

步骤4：绕 yb轴反向旋转90°回到初始位置1。

整个旋转过程如图3所示。

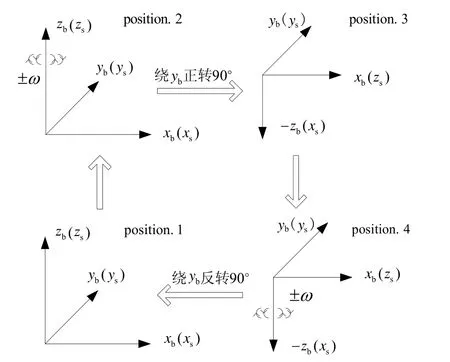
图3 系泊状态下对准标定双轴转位示意图Fig.3 Schematic diagram of dual-axis rotation for alignment and calibration on mooring base

3.2 仿真结果与分析

水平阻尼模式下，误差估计曲线图如图4所示。

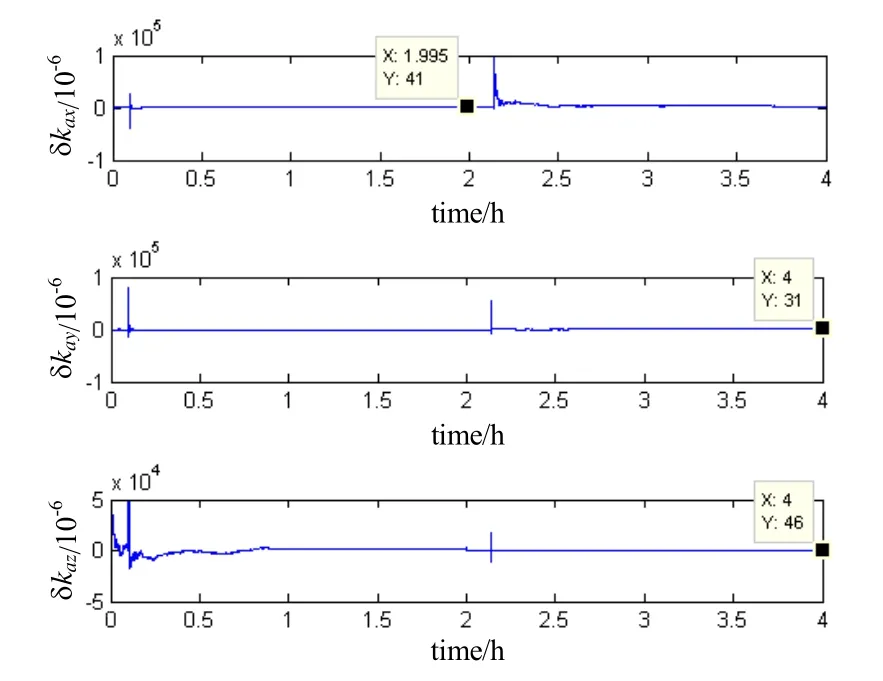
图4 加速度计标度因数误差的估计曲线Fig.4 Estimating curves of accelerometer scale factor error

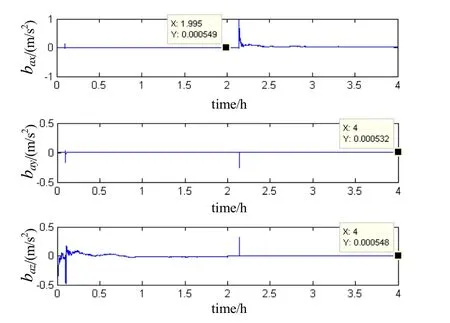
图5 加速度计零偏的估计曲线Fig.5 Estimating curves of accelerometer bias

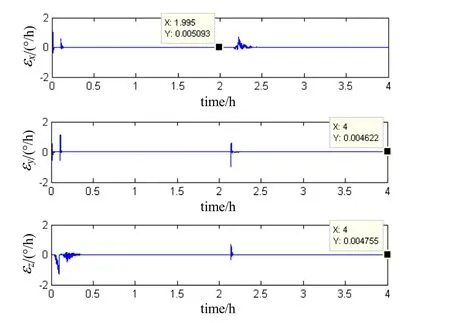
图6 陀螺零偏的估计曲线Fig.6 Estimating curves of gyroscope bias

数据处理结果表明：由于标定方案是通过旋转双轴框架，采用两次绕垂向轴进行单轴旋转，可以使得与转轴垂直方向上的惯性元件误差得到充分激励，提高了可观测性。图 4～6分别代表水平阻尼模式下加速度计标度因数误差、零偏和激光陀螺零偏的估计曲线图，仿真实验时间长度共计4 h，在2 h结束时可以估计出δkax、δkay、bax、bay、εx、εy，在4 h结束时可以估计出δkay、δkaz、bay、baz、εy、εz。

从图4～6中标记部分可以看出，在4 h的仿真过程中，此种方法能够实现对加速度计标度因数误差、零偏和陀螺零偏这9项误差参数的估计。其中加速度计零偏估计误差在设定值 2%以内，陀螺零偏估计误差在设定值8%以内，估计精度基本满足系统精度要求；但对加速度计标度因数误差估计精度较低，最大相对估计误差可达25%，这是由于载体处在横纵摇摆运动状态下，重力加速度g通过姿态分解投影到水平加速度计，再通过耦合标度因数误差δkai后产生的等效加速度计零偏▽i。整个传递过程都是受重力加速度g激励完成的，因此加速度计的随机噪声（零偏稳定性）的大小最终决定了标定因数误差的量级[6,12]。简单的估算形式可以表示为：15μg/1g=15×10-6。图4的标定仿真结果基本上符合了这一情况，说明了加速度计的标度因数误差δkai不能得到较高精度的估计，但可作为一种折中的误差补偿手段。

4 结 论

结合分立式标定的惯性元件安装误差精度高以及激光陀螺标度因数稳定度高的特点，针对惯性元件具有逐次启动误差、一次通电稳定的特点，构造了惯性元件9参量误差模型，利用一阶水平阻尼的参量模型，共同构造了20维误差方程的Kalman滤波器。由于系泊状态下位置信息精确已知，采用水平阻尼方案，能有效抑制惯性元件非平稳的随机漂移等杂散误差源所带来的系统振荡性的输出误差。仿真结果表明，当惯性元件存在较大的随机误差条件下，此方案能使惯性元件的9个误差项得到一定程度上的估计，因此，作为一种系统级姿态初始对准及惯性元件误差标定方法，具有较高的工程应用价值。

（References）：

[1] Levinson E, Majure R. Accurary enhancement techniques applied to the marine ring laser inertial navigator (MARLIN) [J]. Journal of the Institute of Navigation, 1987, 34(1): 64-86.

[2] Yuan Ballun, Liao Dan, Han Songlai. Error compensation of an optial gyro INS by multi-axis rotation[J]. Measurement Science and Technology, 2012, 23(2): 025102.1-9.

[3] 翁海娜，姚琪，胡小毛. 舰船单轴旋转激光捷联惯导系统动态初始对准[J]. 中国惯性技术学报，2012，20(1)：34-38.

WENG Hai-na, YAO Qi，HU Xiao-mao. Dynamic inertial alignment for single-axis rotation laser gyro SINS on the board ship[J]. Journal of Chinese Inertial Technology, 2012, 20(1): 34-38.

[4] 黄凤荣，侯斌，孙伟强，等. 双轴旋转式SINS自主标定技术[J]. 中国惯性技术学报，2012，20(2) : 146-151.

HUANG Feng-rong, HOU Bin, SUN Wei-qiang. Selfcalibration for dual-axis rotary SINS[J]. Journal of Chinese Inertial Technology, 2012, 20(2): 146-151.

[5] Xie Bo, Qin Yongyuan, Wan Yanhui. A high-accuracy calibration method of optical gyro SINS[C]//3rd international symposium on Aeronautics and Astronautics. Harbin, 2010: 507-510.

[6] Zhang Hongliang, Wu Yuanxin, Wu menqi, et al. Improved multi-position calibration for inertial measurement unit[J]. Measurement Science and Technology, 2010, 21(1): 015107.1-11.

[7] 卢雁. 基于速度阻尼的天文/惯性组合导航技术研究[J].光学与光电技术，2012,10(4): 62-67.

LU Yan. Study of CNS/INS integrated navigation system based on speed damping technology[J]. Optics & Optoelectronic Technology, 2012, 10(4): 62-67.

[8] 周章华，徐海刚，吴亮华，等. 单轴旋转SINS方位陀螺漂移分析与估计[J]. 中国惯性技术学报，2013，21(1)：31-36.

ZHOU Zhang-hua, XU Hai-gang, WU Liang-hua, et al. Analysis and estimation for azimuth gyro drift of single-axis rotation SINS[J]. Journal of Chinese Inertial Technology, 2013, 21(1): 31-36.

[9] Savage P G. Strapdown analytics[M]. Maple Plain. Minnesota: Strapdown Associates, Ins., 2007.

[10] Kenneth R. Britting. Inertial navigation systems analysis [M]. Artech House Publishers, 2010.

[11] 杨晓霞，孟浩然，王帅. 激光捷联惯导系统的外场动态标定方法[J]. 中国惯性技术学报，2011，19(4)：393-398.

YANG Xiao-xia, MENG Hao-ran, WANG Shuai. Calibraiton method for laser gyro SINS under outer field dynamic conditions[J]. Journal of Chinese Inertial Technology, 2011, 19(4): 393-398.

[12] Bekkeng J K. Calibration of a novel MEMS inertial reference unit[J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(6): 1967-1974

Calibration method for two-axis indexing RLG-SINS with speed damping

WANG Bin1, WENG Hai-na2, WANG Zhan-qing3, ZHANG Yu-fei2, HU Xiao-mao2
(1. School of Mechanical Engineering, Tianjin University, Tianjin 300072, China; 2. Tianjin Navigation Instrument Research Institute, Tianjin 300131, China; 3. School of Automation, Beijing Institute of Technology, Beijing 100081, China)

The long-term stability of inertial element parameters determines the accuracy of inertial navigation systems, and the present laser gyroscope strapdown inertial navigation system(RLG-SINS) is mainly by means of systematic modulation techniques to achieve the capability of high accuracy navigation or improve the accuracy of initial alignment and the observability of inertial component errors. According to the inertial component error characteristics of RLG-SINS, and combining with the respective advantages of discrete calibration and systematic calibration, a Kalman filter scheme is designed in lever-damp mode to achieve the initial alignment and to calibrate parts of inertial component errors by observing navigation position errors and using two-axis indexing. This scheme can effectively reduce the influence of inertial component’s each startup error on navigation accuracy. The simulation results show that the total nine error parameters (scale factor error and bias of the quartz accelerometer, laser gyroscope bias) can be estimated on mooring base during 4 h operation in zero-speed damping mode. The estimated error for accelerator bias is less than 2%, and the estimated error for gyroscope bias is less than 8%, meeting the demands of high accuracy inertial navigation, and showing that this method has certain engineering practicability.

speed damping; two-axis rotation modulation; systematic calibration; mooring base

联 系 人：翁海娜（1969—），女，研究员，博士后。E-mail：hainaweng@eyou.com

1005-6734(2014)04-0421-05

10.13695/j.cnki.12-1222/o3.2014.04.001

U666.1

A

2014-03-230；

2014-07-21

国防科技重点预研项目（51309030101）

王彬（1986—），男，博士研究生，从事导航、制导与控制研究。E-mail：wang_bin@tju.edu.cn