应用于雷达方位超分辨的改进Richardson－Lucy算法*

邹建武，祝明波董 巍，李相平

(1.海军航空工程学院，山东烟台264001;2.海军航空管制设备维修中心，北京100071)

1 引言

雷达方位超分辨就是在不改变雷达工作体制前提下，利用数字信号处理技术分辨同一雷达波束内的几个等距目标，一直以来都是雷达探测领域研究的热点。主要的方位超分辨方法有迭代反卷积法、RL算法、广义逆滤波法和维纳逆滤波算法等[1－9]。

Mark A.Richards等[1]提出了一种约束迭代反卷积法(CID)和一种快速迭代反卷积法 (FCID)，CID算法在特定情况下，方位分辨力改善了4倍，但算法收敛速度慢，计算量较大;FCID虽然提高了运算速度，但是分辨性能下降。文献[2－3]利用基于Bayesian准则的RL算法实现了雷达方位超分辨，并对算法的超分辨性能进行了深入研究，该算法在信噪比0 dB条件下，方位分辨力提高2倍。但是，上述两种方法均是基于噪声分布为泊松分布的情况下。丁义元等[4]提出利用广义逆滤波方法提高实孔径雷达角分辨力，在高信噪比的条件下，有效地改善了实孔径雷达的角分辨力，但时域计算较为复杂。文献[5－7]利用维纳逆滤波算法对提高雷达方位角分辨力进行了研究，在雷达回波信噪比大于30 dB的情况下，该方法可实现方位超分辨，证明了维纳逆滤波算法实现方位超分辨是可行的，但不适用于低信噪比条件。

RL 算法由 Richardson[8]和 Lucy[9]先后独立提出，主要用于射电天文学和医学中图像的复原，具有良好的频谱外推能力，但其是基于噪声分布为泊松分布的分辨算法。本文将RL算法应用于噪声服从高斯分布的雷达方位超分辨问题中，在噪声存在的条件下，虽然RL算法也能分辨目标，但噪声使得分辨结果出现虚假目标，且RL算法收敛速度慢。本文针对上述问题，将去噪和加速RL算法相结合，得到一种改进RL算法，应用于高斯噪声条件下雷达超分辨问题中。

2 雷达方位回波信号统计观测模型

为简化分析，仅考虑方位角的变化。假设常规雷达在方位向上扫描，实孔径雷达的方位回波信号表现为天线方向图与目标方位信息卷积，雷达目标方位回波模型可以表示为

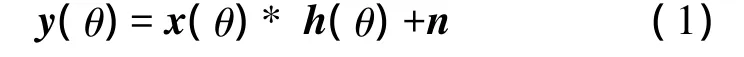
式中，x(θ)为目标方位信息;h(θ)为雷达天线方向图;n为加性噪声，主要是接收机噪声，本文主要考虑加性噪声。将式(1)转换为矩阵－向量表达式:

其中:

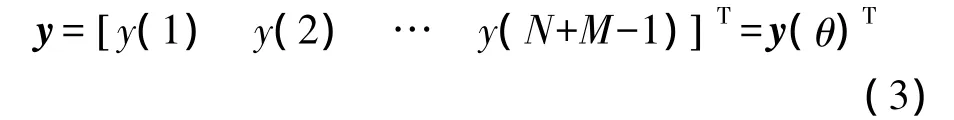
式(2)解释为雷达方位回波信号统计观测模型，当n～pn(n)，假设y中每个元素的分布是相互独立 ，则有

因此，雷达超分辨问题可以转化为参数估计问题，常见的估计方法有极大似然估计，最大后验概率估计和矩阵估计方法。

3 RL算法及其改进

3.1 RL 算法

RL算法是一种具有频谱外推能力的迭代算法，假设噪声为泊松分布。采用最大似然法进行估计，通过Picard迭代算法得到如下迭代公式:

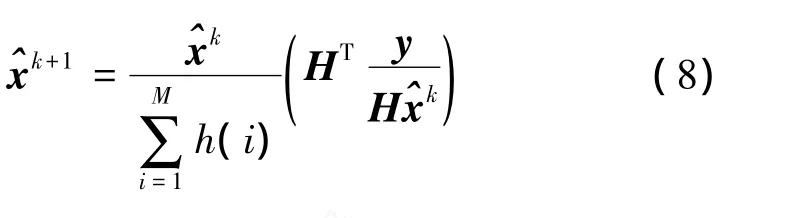
3.2 改进 RL算法

RL算法是一种最大化可能性数据逼近算法，该算法在噪声影响可忽略或较小时，随着k不断增大，会依概率收敛于x;但在噪声不可忽略，尤其是在低信噪比条件下，经过多次迭代，恢复的目标中会出现虚假目标，在应用RL算法过程中，为消除噪声的影响，在出现虚假目标或者算法结果变差以前，终止迭代[2]，因而RL算法难以获得较好的超分辨效果，且RL算法收敛速度较慢。基于上述问题，本文对RL算法进行了改进。

当存在噪声时，将式(2)代入式(8)得

从上式可知，若存在噪声，则上述的收敛性难以保证，存在噪声被放大的缺陷，消除噪声对RL算法很重要。由于雷达目标回波信息主要集中分布在低频段，噪声的信息主要集中在高频段，因此我们将高频段的噪声去除，来降低噪声对RL算法的影响。

综上所述，本文中的改进RL算法，首先利用低通滤波器[11]对雷达目标信号进行去噪处理，同时鉴于RL算法收敛速度慢的缺点，我们利用加速RL算法[12]来对滤波后的信号进行超分辨运算，改进RL算法的迭代公式

式中，accRL(·)为加速RL算法，Y(ω)为y的傅里叶变换，G(ω)为低通滤波传递函数，F－1为傅里叶逆变换。加速RL算法是一种矢量外推加速方法，其数学表达如下:

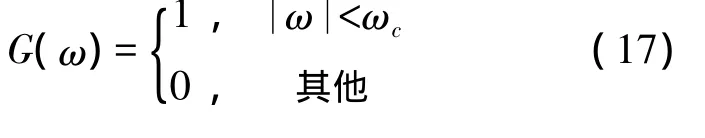
3.3 迭代次数选择

RL算法迭代次数直接影响方位超分辨结果和计算时间。在低信噪比条件下，用RL算法得到的结果会先接近真实目标，再偏离真实目标。本文选用基于均方误差(MSE)准则的迭代次数选择方法:

在不存在噪声时，随着迭代的进行，MSE的值会变小，最后趋于平稳，考虑到超分辨效果和计算时间，此时选择使MSE值趋向平稳时的最小迭代次数即可。在存在噪声的条件下，随着迭代的进行，MSE的值会先变小，后变大，此时可选择MSE值最小时的迭代次数作为算法的总迭代次数。

4 RL算法与改进RL算法对两点目标的分辨性能仿真

4.1 无噪声条件下RL算法仿真

假设脉冲重复频率为1 kHz，扫描速度为100°/s，扫描范围为－15°～15°，天线方向图采用辛克型，半功率波束宽度为2.7°。在不存在噪声条件下，用RL算法对间隔1/2半功率波束宽度的两个等幅点目标(分别位于－0.675°和 0.675°)进行了分辨，分辨结果与相应的均方误差如图1和图2所示。

图1 无噪声条件下的分辨结果Fig.1 Resolution result without noise

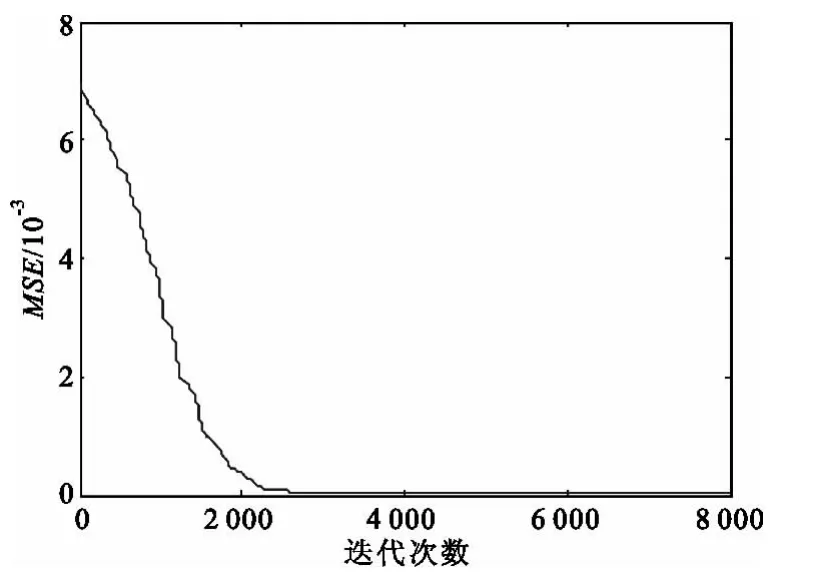
图2 均方误差Fig.2 MSE

上述的仿真条件是针对小型实孔径雷达平台提出的，研究雷达对海或对空搜索目标时的雷达目标方位超分辨问题，此仿真不考虑真实场景的影响。图1中的*表示点目标的实际位置，由图可看出，无噪声时，利用RL算法可以分辨出间隔1/2半功率波束宽度的两个点目标，且随着迭代次数的增加，MSE值趋于零。此时综合考虑，我们选择终止迭代次数为2 000。

4.2 噪声存在条件下RL算法与改进RL算法仿真

针对上述仿真参数，分别利用RL算法和改进RL算法，在信噪比分别为30 dB和20 dB条件下对方位间隔分别为1/4和1/2半功率波束宽度的两个等幅点目标进行了分辨，仿真结果如图3～6所示。

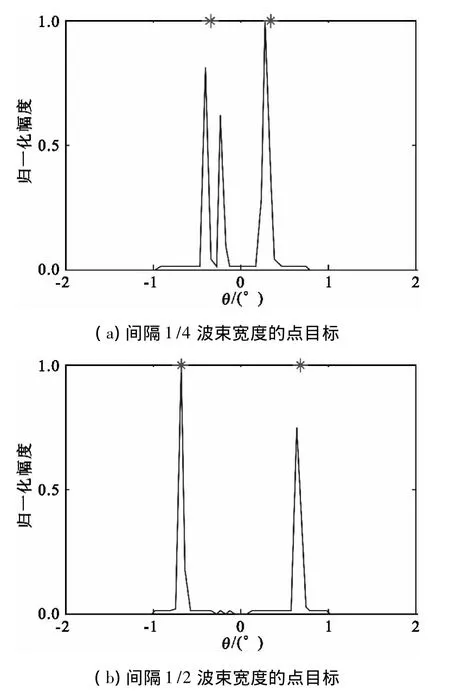
图3 30 dB条件下RL算法结果Fig.3 Results of RL algorithm with SNR=30 dB

图4 30 dB条件下改进RL算法结果Fig.4 Results of improved RL algorithm with SNR=30 dB

图5 20 dB条件下RL算法结果Fig.5 Results of RL algorithm with SNR=20 dB

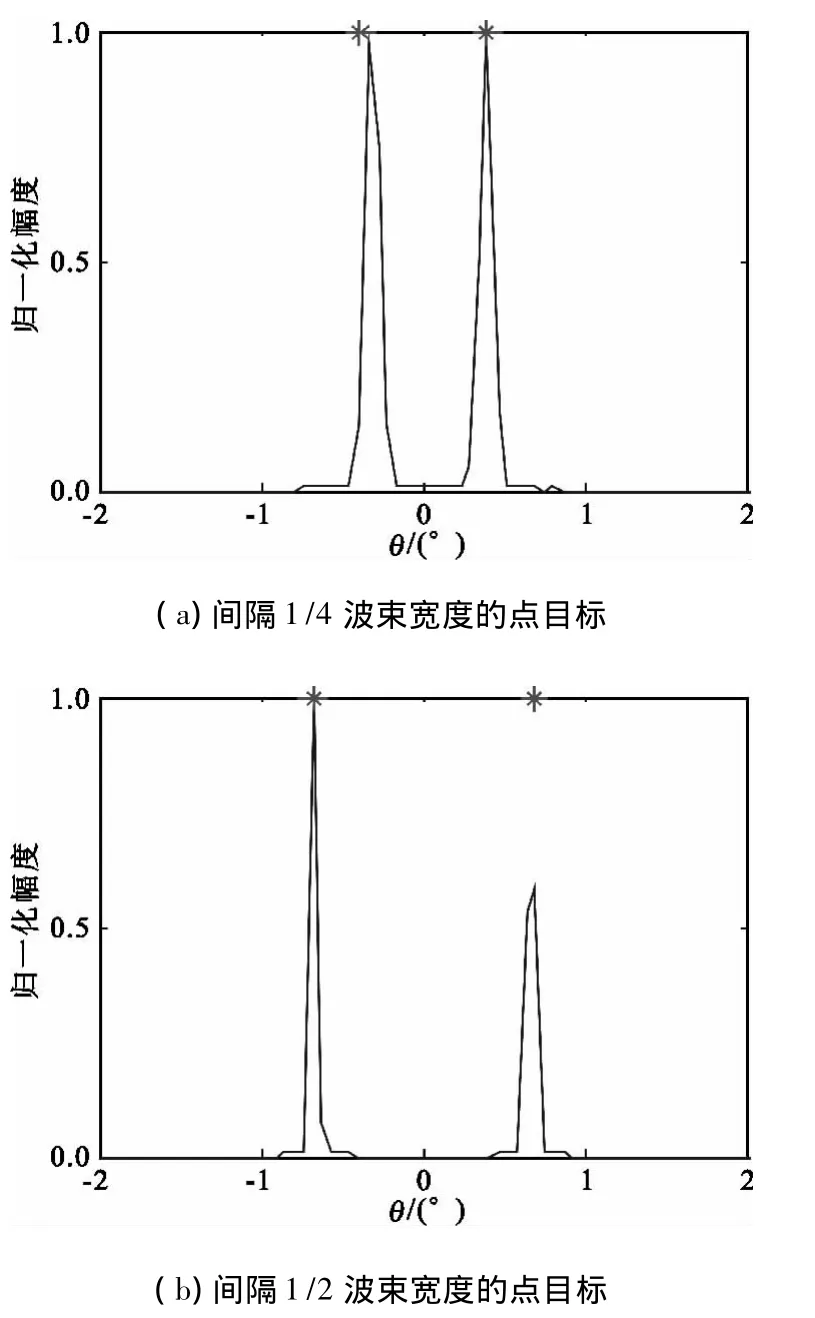
图6 20 dB条件下改进RL算法结果Fig.6 Results of improved RL algorithm with SNR=20 dB

由图3和图5可看出，在噪声存在条件下，利用RL算法进行分辨目标，当两个目标间隔为1/2半功率波束宽度时，噪声对分辨结果没造成太大影响，如图3(b)和图5(b)所示。但是，随着两目标间隔的缩小，噪声会使得分辨结果产生虚假目标，如图3(a)和图5(a)所示。

由图4(a)和图6(a)可看出，在噪声存在条件下，利用改进RL算法能够分辨两个点目标，而不产生虚假目标。与图3(a)和图5(a)相比，改进RL算法在一定程度上，可以降低噪声对分辨结果的影响。由此可看出，改进RL算法可用于高斯噪声条件下的雷达方位超分辨问题的研究。

需要注意的是，由于RL算法受噪声影响，产生虚假目标，导致算法性能不稳定，因此我们用维纳逆滤波算法与改进RL算法相比较，在不同信噪比条件下，两种方法对两个等幅点目标所能分辨的最大分辨倍数(半功率波束宽度/改进RL算法所能分辨的两目标间隔的最小角度)如表1所示。

表1 改进RL和维纳逆滤波算法的分辨性能Table1 Performance of improved RL algorithm and Wiener inverse filtering algorithm

由表1可知，随着SNR值的降低，算法的分辨性能下降。与维纳逆滤波相比，改进RL算法可在低信噪比条件下分辨两个点目标，当噪声为0 dB时，虽然此时能分辨目标，但是由于低频段噪声的影响，使得改进RL算法的分辨精度变差，且有可能出现虚假目标，如何降低低频段噪声的影响还有待于进一步研究。

5 结束语

利用RL算法良好的频谱外推能力对雷达方位超分辨问题进行了研究，主要针对RL算法存在噪声被放大的缺陷，提出一种改进RL算法来降低噪声的影响。初步仿真结果表明，改进RL算法能降低噪声的影响，可用于雷达方位超分辨，与维纳逆滤波相比，噪声适应性更好，具有一定的实际应用价值。但在低信噪比条件下，改进RL算法的分辨性能下降，如何减小低信噪比条件下低频段噪声的影响尚待进一步研究。

[1]Richards M A.Iterative Noncoherent Angular Superresolution[C]//Proceedings of 1988 IEEE National Radar Conference.Ann Arbor，MI:IEEE，1988:100－105.

[2]李惠.实孔径雷达波束锐化算法研究[D].成都:电子科技大学，2010.LI Hui.Research on Beam Sharpening Algorithm of Real Aperture Radar[D].Chengdu:University of Electronic Science and Technology of China，2010.(in Chinese)

[3]Li D Y，Huang Y L，Yang J Y.Real Beam Radar Imaging Based on Adaptive Lucy－Richardson Algorithm[C]//Proceedings of 2011 IEEE Radar Conference.Chengdu:IEEE，2011:14－17.

[4]丁义元，杨建宇，张卫华，等.改进实孔径雷达角分辨力的广义逆滤波方法[J].电子学报，1993，21(9):15－19.DING Yi－yuan，YANG Jian－yu，ZHANG Wei－hua，et al.Improvement of Angular Resolution of Real Aperture Radar Via Generalized Inverse Filtering[J].Acta Electronica Sinica，1993，21(9):15－19.(in Chinese)

[5]单荣光，李士国，朱力.去卷积实现雷达方位超分辨[J].现代雷达，1993(6):25－32.SHAN Rong－guang，LI Shi－guo，ZHU Li.Radar Azimuth Super－resolution Using Deconvolution[J].Modern Radar，1993(6):25－32.(in Chinese)

[6]Zhao K，Wang J G.Improved wiener filter superresolution algorithm for passive millimeter wave imaging[C]//Proceedings of 2011 IEEE Radar Conference.Chengdu:IEEE，2011:1768－1771.

[7]高明哲，祝明波.噪声对维纳滤波反卷积算法性能影响的分析[J].舰船电子工程，2012，32(12):35－37.GAO Ming－zhe，ZHU Ming－bo.Analysis on Noise's Impact on the Performance of Wiener Filter Deconvolution Algorithm[J].Ship Electronic Engineering，2012，32(12):35－37.(in Chinese)

[8]Richardson W H.Bayesian－based iterative method of image restoration[J].Journal of the Optical Society of A-merica，1972，62(1):55－59.

[9]Lucy L B.An iterative technique for the rectification of observed distributions[J].The Astronomical Journal，1974，79(6):745－754.

[10]周昌雄，苏品刚，颜廷泰，等.应用改进自蛇模型和LR算法恢复毫米波图像[J].激光与红外，2012，42(4):468－472.ZHOU Chang－xiong，SU Pin－gang，YAN Ting－tai，et al.Millimeter wave image restoration based on the improved self－snake model and L－R algorithm[J].Laser＆ Infra-red，2012，42(4):468－472.(in Chinese)

[11]王志明，殷绪成.数字图像处理与分析[M].北京:清华大学出版社，2012:72－73.WANG Zhi－ming，YIN Xu－cheng.Digital image processing and analysis[M].Beijing:Tsinghua University Press，2012:72－73.(in Chinese)

[12]David S，Biggs C，Andrews M.Acceleration of Iterative Image Restoration Algorithms [J].Applied Optics，1997，36(8):1766－1775.