基于自相关函数相位的正弦信号频率估计新算法*

黄 超，索继东，于 亮

(1.大连海事大学信息科学技术学院，辽宁大连116026;2.大连理工大学城市学院电子与自动化学院，辽宁 大连116600;3.大连理工大学 软件学院，辽宁 大连116600)

1 引言

对淹没于噪声中的正弦信号进行频率估计，无论在理论中还是在实际应用中都具有非常重要的研究价值，国内外众多学者对此做了大量的研究，主要从频域和时域两个角度进行分析，如基于FFT的频率估计算法[1－2]。本文从时域的角度对频率估计算法进行研究。传统基于时域的自相关方法有:V.Pisarenko利用少量的自相关函数进行频率估计[3]，此类方法计算简单，但其性能不高;K.Lui等人在在文献[3]的基础上加以改进，并定义新的自相关函数[4]，但由于选取的自相关函数系数较低，估计性能受到限制;K.Lui等人在文献[4]的基础上加以修正，采用较高序号的自相关系数[5]，使得估计性能得到一定的提升，但是在信噪比偏低时，估计性能不够理想;为了充分挖掘自相关函数包含的频率信息，Rim，H.C.So，Yan Cao等人尽可能地利用多个自相关函数进行频率估计[6－8]，使得估计性能得到很大提升，但同时算法的计算量也增大;为了进一步提升频率估计性能，K.Lui提出了两步自相关算法[9]，Yan Cao等人提出了基于扩展自相关的频率估计算法[10]，在低信噪比估计性能得到进一步改善，在中高信噪比时，频率估计方差接近克拉美罗下界(CRLB)[11]。然而，在现有很多算法中，估计性能的提升都是利用更多的自相关系数或者多步自相关函数，这样必然会带来算法计算量的增大，即存在频率估计精度与算法复杂度的矛盾问题。

为了解决上述问题，本文同样从自相关函数的角度，充分利用自相关函数包含的频率信息，推导了一种新的自相关函数相位的频率估计式，并且针对频率估计范围与频率估计精度之间的矛盾问题，提出了一种消除相位模糊的方法。计算机仿真表明，在信噪比较高时，估计方差接近克拉美罗下界(CRLB)，与TSA算法相比，在估计性能相同条件下，本文算法的计算量大大降低，具有很好的应用价值。

2 正弦信号频率估计算法原理

设混有高斯加性白噪声的单频正弦信号表示式为

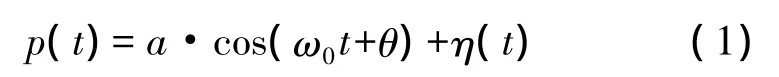
其中，a、ω0、θ分别为信号的幅度、频率、相位，η(t)为均值为零、方差为σ2的加性高斯白噪声。对其在观察时间0≤t≤T内进行采样N个样本值，于是得到离散序列为

对上式定义其自相关函数为

当N足够大时，由文献[10]可知，式(3)可写为

Pisarenko[3]算法利用低阶自相关 r1、r2进行频率估计，如下式所示:

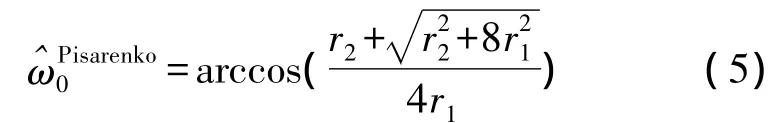
Pisarenko算法虽然计算量小，但是频率估计方差和CRB相差较大。为了进一步减小频率估计偏差，K.Lui等人在PHD算法的基础上加以改进，提出了K.Lui算法[4]。其算法仅对Pisarenko算法的r1、r2进行重新定义，改进了r1、r2的估计性能，如下式所示:

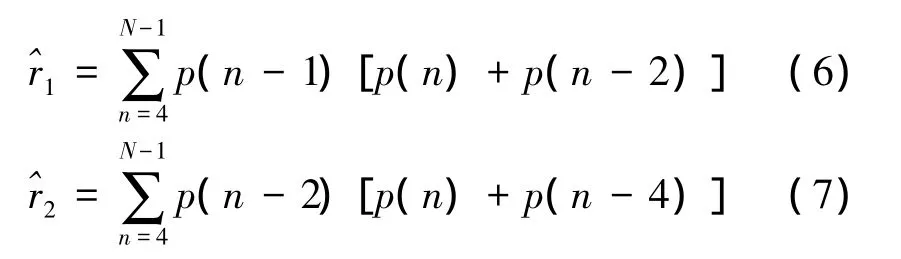
于是，式(5)可改写为

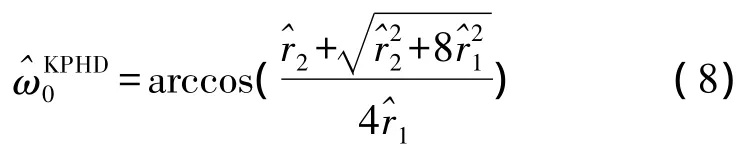
为了进一步提高载波频率估计性能，TSA算法[9]利用更多的自相关函数进行频率估计:

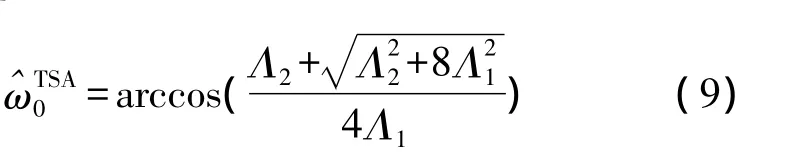
其中:

从上式可以看出，TSA算法经过自相关函数的多次组合，充分挖掘自相关函数包含的频率信息进行频率估值，理论分析及仿真结果表明，SNR≥0 dB时，频率估计方差接近CRLB，且频率估计范围宽;但是其算法的计算量较大(与O(N3)成正比)，不利于实时信号的处理。

3 本文提出的新的频率估计式

目前，基于自相关函数的频率估计算法中，很多都是通过利用多个自相关系数，使得频率估计的性能得到提升，如 Yan 算法[8，10]、TSA 算法[9]等，但同时会带来计算量的增加，不利于实时通信的信号处理。针对频率估计精度与算法复杂度的矛盾问题，本文从自相关函数相位的角度，推导了一种新的频率估计式，较好地解决了上述矛盾问题。

由正弦信号的三角函数特性可知

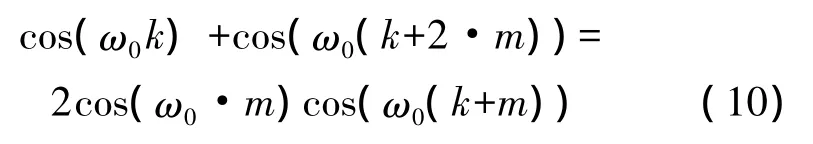
于是，可得下式:

为了进一步提高频率估计性能，对上式进行展开:

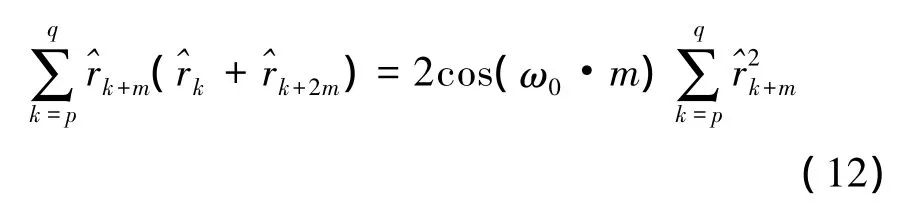
其中，p≥1，p≤q≤N－2m－1。于是，可得出本文新的频率估计式:

式中，ξm为整数。

为了研究参数(p，q，m)对频率估值的影响，对上式进行了仿真。在仿真中，当(m，p，q·m)在(0，π)范围内时，此时 ξm=0，令信号幅度 a=1，θ=0，ω0=0.01π，SNR=10 dB，N=200，p=1(蒙特卡洛仿真100次)。图1给出了m=1时不同q值时的频率估计方差，从图1可以看出，随着q值增大，估计性能不断提升，当q为50左右时，估计性能逐渐接近最佳值。图2给出了q=1时不同m取值的估计方差，从图2可以看出，当m为60左右时，频率估计性能最佳。

由上式可得频率估计值为

图2 不同m值的估计性能Fig.2 Mean square error versus m

以上仿真中，假设频率范围为(0，π/m)。从图1和图2可以得出，为了提高频率估计精度，(p，q，m)参数的取值很关键，不难得出(p=1，q=50，m=60)的性能会好于(p=1，q=50，m=1)及(p=1，q=1，m=60)的性能;而m＞1时会缩小频率估计范围，为了扩大估计范围，即m，p，q∈(0，π)，此时ξm有2m+1种可能的值，即存在相位模糊问题，为了准确地找出 ξm值，消除相位模糊，可采取以下措施(令 m=1，2，…，ε，):

(1)m=1，此时不存在相位模糊问题，即ξ1=0，可求出频率估计值1，p，q;(2)m=2，求出

时对应的 ξ2，再根据式(13)求出频率估计值(|·|min为取最小值);

(3)以此类推;

(4)m=ε，求出

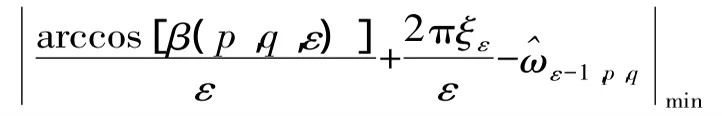
时对应的ξε，再根据式(13)求出频率估计值ε，p，q。

综上可知，q值的增大会带来频率估计精度的提升，但同时会导致计算量过大，因此，在实际应用中，应综合考虑估计性能和计算量之间矛盾的问题。

4 计算量及性能分析

图1 不同q值的估计性能Fig.1 Mean square error versus q

4.1 计算机仿真及性能分析

本节通过计算机MATLAB仿真实验(蒙特卡洛仿真100次)来验证本文提出算法的估计性能。图3给出SNR=10 dB时不同频率处的性能比较，本文频率估计算法的性能(m=50，p=1，q=70)在 ω0∈[0.15π，0.85π]达到 CRLB，频率估计范围与 TSA算法[9]相当，都宽于 K.Lui算法[5]的频率估计法范围。图4给出了ω0=0.3π、N=200时不同信噪比下各种算法的性能比较，可以看出，在SNR＞0 dB时，随着信噪比增大，本文算法(m=50，p=1，q=50，m=50，p=1，q=70 及m=50，p=1，q=80)与TSA 算法的估计性能相当，都接近于CRLB，且性能都好于K.Lui算法[5];在 SNR＜0 dB 时，随着 SNR 的减小，估计性能偏离CRLB的程度从大到小依次为K.Lui算法[5]、本文算法(m=50，p=1，q=50)、本文算法(m=50，p=1，q=70)、本文算法(m=50，p=1，q=80)和 TSA 算法[9]。

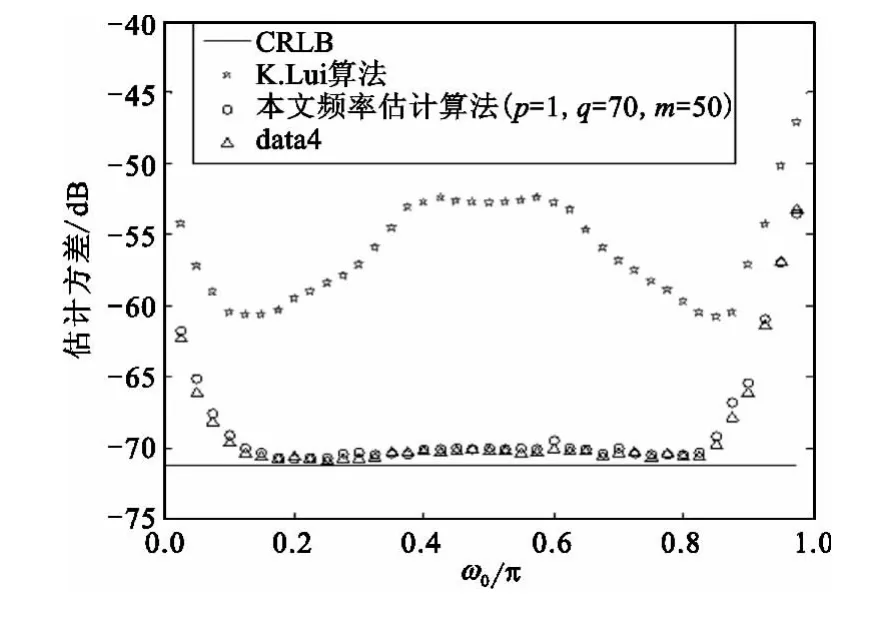
图3 不同频率处的性能比较Fig.3 Mean square error versus ω0

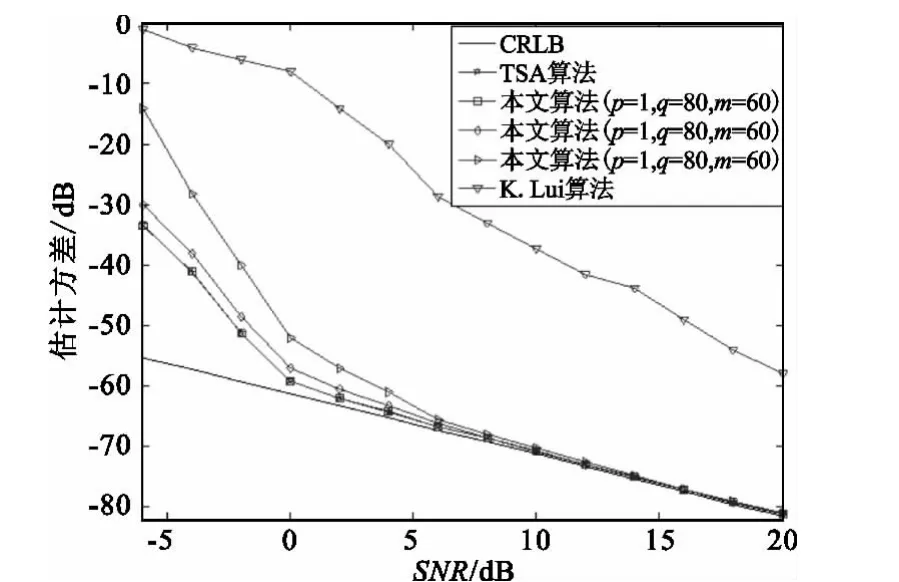
图4 不同信噪比下的性能比较Fig.4 Mean square error versus SNR

综上分析可得，在信噪比较高时，本文算法中q值可以选择较小(q值越小，计算量越小)，如q=50，其估计性能也接近CRLB;在信噪比较低时，本文算法中q值可以选择较大，如q=80，其估计性能偏离CRLB最小。

4.2 算法复杂度比较

从表1可以看出，本文算法的计算量(与 O(N2)成正比)高于 K.Lui算法[5]，低于 TSA算法[9]的计算量(与 O(N3)成正比)。由式(8)、式(9)、式(13)可以看出，K.Lui算法[5]只利用几个自相关系数进行频率估计，本文算法利用多个自相关系数且通过递推的方式求出频率值，而TSA算法[9]是在一步自相关的基础上再作自相关运算，其计算量最大。从图4的仿真结果来看，本文算法(m=50，p=1，q=80)与TSA算法的频率估计性能非常接近，但本文算法的计算量约为TSA算法[9]的2/5，非常有利于信号的实时处理。

表1 算法计算量比较Table1 Comparison of arithmetic operations

5 结论

充分利用自相关函数包含的频率信息进行频率估计，可以使估计性能得到提升。本文针对加性高斯白噪声的正弦信号，提出了基于加窗自相关函数相位噪声的频率估计算法。文中推导了自相关函数相位噪声的频率估计式，并针对频率估计范围与频率估计精度之间的矛盾问题，提出了一种消除相位模糊的方法。仿真结果表明，在信噪比较高时，估计方差接近克拉美罗下界(CRLB)，且在估计性能相同条件下，与TSA算法相比，本文算法的计算量大大降低，在工程上具有很好的应用价值。

然而，在现有的众多算法中，低信噪比时的估计性能还是不够理想，如何更好地挖掘自相关函数包含的频率信息，降低频率估计的信噪比阀值，将是我们进一步研究的内容。

[1]王宏伟，赵国庆，齐非林.一种实时精确的正弦波频率估计算法[J].数据采集与处理，2009，24(2):208－211.WANG Hong－wei，ZHAO Guo－qing，QI Fei－lin.Real－Time and Accurate Single Frequency Estimation Approach[J].Journal of Data Acquisition ＆ Processing，2009，24(2):208－211.(in Chinese)

[2]路伟涛，杨文革，洪家财，等.一种新的正弦信号频率和初相估计方法[J].电讯技术，2012，52(9):1459－1464.LU Wei－tao，YANG Wen－ge，HONG Jia－cai，et al.A Novel Method for Frequency and Initial Phase Estimation of Single－ tone Signals[J].Telecommunication Engineering，2012，52(9):1459－1464.(in Chinese)

[3]Pisarenko V.The retrieval of harmonicsby linear prediction[J].Geophysical Journal of the Royal Astronomical Society，1973，33(5):347－366.

[4]Lui K，So H C.Improved Variant of Pisarenko Harmonic Decomposition for Single Sinusoidal Frequency Estimation[J].IEICE Transactions on Fundamentals of Electronics，Communications and Computer Sciences，2007，90(11):2604－2607.

[5]Lui K，So H C.Modified Pisarenko Harmonic Decomposition for Single－tone frequency estimation[J].IEEE Transactions on Signal Processing，2008，56(7):3351－3356.

[6]Elasmi－Ksibi R，Besbes H，L pez－Valcarce R，et al.Frequency estimation of real－valued single－tone in colored noise using multiple autocorrelation lags[J].IEEE Transactions on Signal Processing，2010，90(7):2303－2307.

[7]So H C，Chan K W.Reformulation of Pisarenko harmonic decomposition method for single－tone frequency estimation[J].IEEE Transactions on Signal Processing，2004，52(4):1128－1135.

[8]Cao Yan，Wei Gang，Chen Fang－Jiong.An exact analysis of Modified Covariance frequency estimation algorithm based on correlation of single－tone[J].IEEE Transactions on Signal Processing，2012，92(4):2785－2790.

[9]Lui K，So H C.Two－stage autocorrelation approach for accurate single sinusoidal frequency estimation[J].IEEE Transactions on Signal Processing，2008，88(7):1852－1857.

[10]Cao Yan，Wei Gang，Chen Fang－Jiong.A ClosedformExpanded Autocorrelation Method for Frequency Estimation of A Sinusoid[J].IEEE Transactions on Signal Processing，2012，92(4):1852－1857.

[11]Funga H W，Alex C，Kotb K H Li，et al.ParameterEstimation of A Real Single Tone from Short Data Records[J].IEEE Transactions on Signal Processing，2004，84(3):601－617.