基于混沌同步的噪声鲁棒测距方法*

刘立东，宋焕生，靳 钊

(长安大学 信息工程学院，西安710064)

1 引言

1990年，美国学者Pecora和Carroll提出了混沌同步理论[1]，这个理论为混沌在保密通信[2－6]、雷达[7－15]以及电子信息[16－17]等方面的应用提供了广阔前景。特别是在雷达方面，混沌同步为雷达信号的噪声抑制、发射信号重构等方面提供了简便的操作方法[13－15]。

混沌雷达是雷达发射信号的幅度、相位或频率通过混沌信号调制的雷达。测距研究是混沌雷达研究的一个重要领域。目前，已有多位学者对混沌雷达测距展开了深入研究。文献[13]提出了一种对发射、接收信号作互相关处理并根据互相关函数的峰值得到目标距离的方法，但是在作互相关处理时由于混沌信号的不确定性和未知性使得混沌雷达发射信号的延迟很难实现;为解决这一问题，文献[14]提出了一种基于Chua's混沌系统同步的测距方法，通过比较发射信号和回波信号的相位差得到目标的距离，但是该方法是在无噪声的条件下实现的;文献[15]提出了一种在低噪声环境下基于混沌信号初始值估计重构雷达发射信号的方法，并通过重构的发射信号和回波信号作互相关处理得到目标的距离。由于实际工程中噪声无处不在，如何在实际工程噪声中实现混沌雷达测距有待进一步研究。

本文提出了一种在噪声环境下通过混沌同步实现对目标距离测量的方法:首先，在混沌雷达发射信号中叠加一个参考正弦信号;然后，让雷达接收信号作为主控信号驱动受控系统，以此产生和发射信号相同混沌的信号，通过这种混沌同步方法可以提取回波信号中带有距离信息的恢复正弦信号;最后通过比较参考正弦信号和恢复正弦信号的相位差得到目标的距离。和文献[14－15]相比，本文方法在噪声环境中可以达到良好的测距效果。

2 “快－慢双频”混沌系统

“快－慢双频”混沌系统是Carroll在2005年提出的一种新型混沌系统[12]。这种混沌系统由快速吸引子和慢速吸引子两个部分组成，其表达式见式(1):

其中 ，c1～c6为常数参数;x1～x3构成快速吸引子，是“快－慢双频”混沌系统中的高频部分;x4～x6是x1～x3的耦合阻尼系统，构成慢速吸引子，是“快－慢双频”混沌系统中的低频部分;c3是“快－慢双频”混沌系统中的阻尼因子，决定了低频部分的频率。例如，当c3=0.01时，x4～x6的频率是x1～x3的1%。

3 “快－慢双频”混沌系统的噪声鲁棒性分析

本文研究发现，Carroll提出的“快－慢双频”混沌系统在同步时具有噪声鲁棒性，是通过系统中的阻尼因子实现的。下面给出“快－慢双频”混沌系统同步的噪声鲁棒原理。

令式(1)表示的混沌系统为主控系统，同步时的受控混沌系统见下式:

受控系统的参数和主控系统一致，其中的n(t)为加性高斯白噪声(混沌雷达选取x2作为发射信号，噪声和x2叠加)。式(2)可以改写成

其中，τ=c3t，当c3→0，高频部分y1～y3的方程可以写成

把式(4)代入式(3)的低频部分(y4～y6)可以得到

式(5)的Jacobian矩阵为

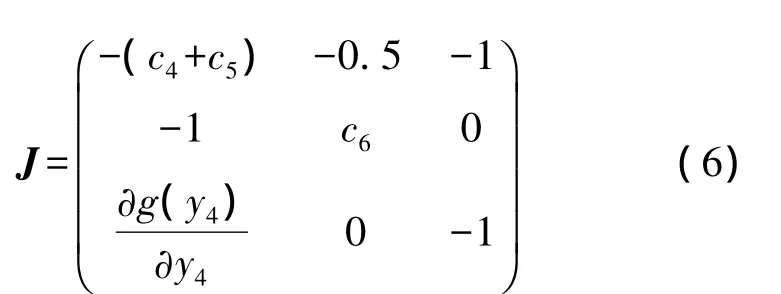
从式(6)中可以看出，高频部分y1～y3没有出现，这意味着低频部分y4～y6没有受到加性噪声的影响，因为加性噪声是叠加在高频信号中(本文噪声叠加在主控系统x2信号中)。事实上，低频部分起到了窄带滤波器的作用，当窄带无限窄的时候，理论上低频部分同步时不会受到噪声的影响。

4 基于混沌同步的噪声鲁棒测距方法

通过对“快－慢双频”混沌系统的研究，本文提出一种建立在混沌同步基础上的新的测距方法，它和已有方法相比，其对噪声的鲁棒性更强。本文方法的思路如下:首先，在“快－慢双频”混沌系统的发射信号中叠加参考正弦信号;然后，让雷达接收信号作为主控信号驱动受控系统，以此产生和发射信号相同混沌的信号，通过回波信号和混沌同步信号的差值可以提取回波信号中带有距离信息的恢复正弦信号;最后，通过比较参考正弦信号和恢复正弦信号的相位差得到雷达回波信号的延迟时间，并通过延迟时间得到目标距离，参见图1。

图1 基于混沌同步的噪声鲁棒测距原理图Fig.1 The schematic of the proposed method fortarget distance measurement

本文雷达发射信号st(t)为

其中，sin(ω1t+θ0)是叠加的参考正弦信号，ω1是固有频率，θ0为初始相位，x2m(t)由下式决定:

回波信号st(t)可表示为

其中，τ表示回波的延迟时间;由于多普勒效应的存在，ω2是不同于ω1的一个角频率;θ1为初相;n(t)为加性高斯白噪声。

令sr(t)为驱动信号，驱动由下式描述的受控混沌系统:

在无噪声的情况下，时间累计到一定程度后，式(10)中 x2s(t－τ)和式(8)中 x2m(t－τ)的输出趋于一致，也就是输出达到同步。此时，sr(t)减去x2s(t－τ)理论上只含有 sin[ω2(t－τ)+θ1]这一项。但是考虑到噪声的存在，则有

其中，εe为由于噪声存在产生的同步误差。从本文第三部分的分析可知，本文选取的“快－慢双频”混沌系统在同步时具有噪声鲁棒性，因此εe是一个很小的值。

接下来，本文详细阐述如何通过计算参考正弦信号和通过混沌同步恢复的正弦信号的相位差来得到目标的距离。令恢复的正弦信号为

为了获得恢复正弦信号m(t)和参考正弦信号sin(ω1t+θ0)的相位差，本文采用了一种新方法——希尔伯特变化的方法，而不是和文献[14]一样直接在时域中提取正弦信号的相位差。其原因是:文献[14]的研究背景并无噪声，直接在时域得到两个正弦信号相位差理论上不会产生误差;而在噪声环境下直接在时域中提取正弦信号相位差会有较大的误差，即使同步误差εe很小，直接在时域中得到的相位差也会有一定的误差。接下来描述如何通过希尔伯特变化的方法得到两正弦信号的相位差。

首先，计算得到m(t)的解析信号

其中，A(t)为 ψ(t)的幅值，θ(t)为 ψ(t)的相位，m'(t)是m(t)的希尔伯特变换，由下式描述:

其中，P.V.表示柯西主值意义下积分。因此，ψ(t)的相位为

雷达回波信号的延迟时间τ为

所以，被测目标的距离可以通过下式得到:

其中，c为光速。

图2 发射信号st(t)波形Fig.2 Transmitted signal st(t)

图3 SNR=0 dB时波形Fig.3 Transmitted signal st(t)under SNR=0 dB

5 数值仿真分析

下面通过仿真实验来验证本文理论的有效性。

令目标距离为1 500 m，信噪比为0 dB，雷达信号带宽为100 MHz，雷达发射信号st(t)由式(7)和式(8)定义，其中式(8)参数 c1=0.02，c2=0.13，c3=0.01，c4=0.1，c5=0.5，c6=0.1。根据文献[12]，这些参数的选择保证了“快－慢双频”混沌系统的最大李亚普诺夫指数大于0，即意味着系统进入混沌状态。图2是st(t)信号的波形，图3是st(t)在0 dB噪声背景下的波形。从图3可以明显看出，雷达发射信号已经淹没在噪声中。接下来，使用本文的方法经过混沌同步后恢复出的雷达回波信号sr(t)见图4，从图中可以看出，经过混沌同步后的回波信号明显过滤了噪声，在不考虑时延的情况下，回波信号的幅值和发射信号幅值几乎相同。为了对比，对已有方法，比如文献[14－15]的方法在相同的条件下进行仿真，其效果图见图5和图6。从图5和图6中可以看出，由于噪声的影响，回波信号的幅值和发射信号幅值存在较大的误差，这不利于从回波信号中准确提取正弦信号的相位，因此本文提出的方法在噪声环境下和文献[14－15]相比误差更小。

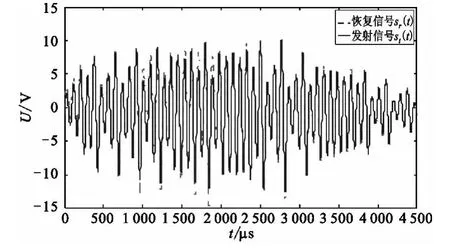
图4 SNR=0 dB时发射信号和通过本文方法后的恢复信号Fig.4 st(t)and the recovered signal through chaotic synchronization method in this paper under SNR=0 dB

图5 SNR=0 dB时发射信号和通过文献[14]方法后的恢复信号Fig.5 st(t)and the recovered signal by using the method in Reference[14]

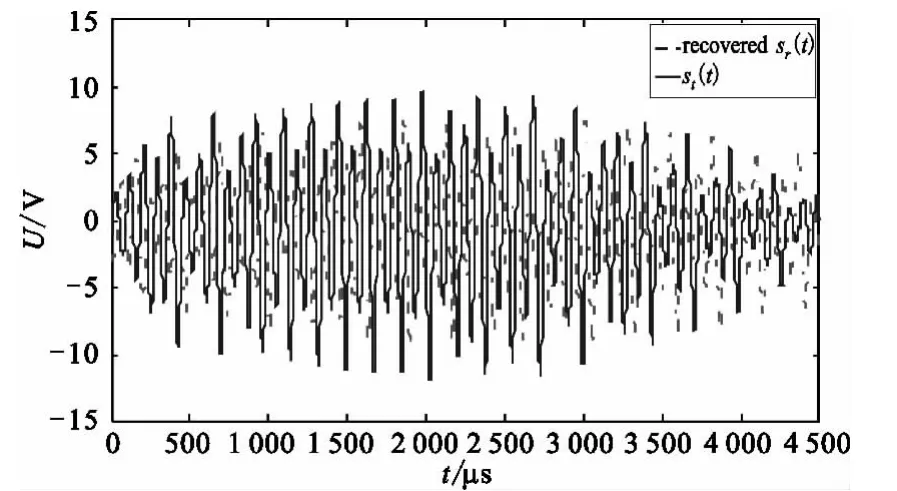
图6 SNR=0 dB时发射信号和通过文献[15]方法后的恢复信号Fig.6 st(t)and the recovered signal by using the method in Reference[15]

接下来，通过本文第4节中希尔伯特变换的方法得到参考正弦信号和恢复正弦信号的相位差，其仿真结果见图7和图8，其中图8是图7的部分放大图。从图8中可以明显看出，参考正弦信号和恢复正弦信号的相位差为0.1 rad，因此通过式(16)计算得到雷达的回波时间是10－5s。最后，通过式(17)计算可以得到目标的距离为1 500 m。

由以上分析可知，虽然文献[14－15]中的方法也可以在无噪声的条件下得到目标的距离，但是随着噪声的增加，其测距效果变差，特别是当信噪比接近0 dB或者信噪比更小的时候，其方法很难实现对目标距离的准确测量。而本文提出的方法具有一定的噪声鲁棒性，在信噪比为0 dB甚至信噪比更小的条件下依然可以实现对目标距离的测量，这种方法为混沌雷达应用于实际工程提供了理论支持。

图7 参考正弦信号和恢复正弦信号的相位Fig.7 The phases of the reference signal and the recovered signal

图8 图7的局部方法图Fig.8 The enlarged figure of Fig.7

6 结论

本文提出了一种基于同步的混沌雷达噪声鲁棒测距方法，并对该方法的噪声鲁棒特性进行了分析，其原理是混沌系统中的低频部分作为噪声滤波器起到了过滤噪声的作用。噪声鲁棒性使得本文方法在混沌同步后能够得到恢复正弦信号的相位，并通过它和发射信号中叠加的参考正弦相位比较得到两者的相位差，从而获得目标的距离。本文方法在0 dB的信噪比环境下可以准确获得目标距离，为混沌雷达应用于实际工程提供了理论支持。考虑到实际雷达工作环境的信噪比往往低于－20 dB，后续的研究工作可以结合文献[18]的噪声抑制算法，先通过抑制噪声来提高信噪比，然后再使用本文的方法得到目标的距离。

[1]Pecora L M，Carroll T L.Synchronization in chaotic systems[J].Physical Review Letters，1990，64(8):821－824.

[2]Ghosh D，Banerjee S.Adaptive scheme for synchronization－based multiparameter estimation from a single chaotic time series and its applications[J].Physical Review E，2008，78(5):1－5.

[3]Wang Kai，Pei Wenjiang，Wang Shaoping，et al.Symbolic Vector Dynamics Approach to Initial Condition and Control Parameters Estimation of Coupled Map Lattices[J].IEEE Transactions on Circuits and Systems I:Regular Papers，2008，55(4):1116－1124.

[4]Wang Kai，Pei Wenjiang，He Zhenya，et al.Estimating initial conditions in coupled map lattices from noisy time series using symbolic vector dynamics[J].Physical Letters A，2007，367(4－5):316－321.

[5]Leung H，Shanmugam S，Xie N.An ergodic approach for chaotic signal estimation at low SNR with application to ultra－wide－band communication[J].IEEE Transactions on Signal Processing，2006，54(5):1091－1103.

[6]Jovic B，Unsworth C.Fast synchronization of chaotic maps for secure chaotic communications[J].Electronics Letters，2010，46(1):1－2.

[7]魏恒东.混沌遥测及其非合作信号检测与参数估计[J].电讯技术，2013，53(6):711－715.WEI Heng－dong.Chaotic Telemetry and its Non－cooperative Signal Detection and Parameters Estimation [J].Telecommunication Engineering，2013，53(6):711－715.(in Chinese)

[8]LIU Li－dong，HU Ji－feng，HE Zi－shu，et al.A Velocity Measurement Method Based on Scaling Parameter Estimation of Chaotic System[J].Metrology and Measurement System，2011，18(2):275－282.

[9]Venkatasubramanian V，Leung H.A novel chaos－based high－resolution imaging technique and its application to through－the－wall imaging[J].IEEE Signal Processing Letters，2005，12(6):528－531.

[10]Kulpa K，Lukin K，Miceli W，et al.Editorial Signal Processing in Noise Radar Technology[J].IET Radar，Sonar and Navigation，2008，2(4):229－232.

[11]Carroll T L.Noise－resistant chaotic synchronization[J].Physical Review E，2001，64(1):1－8.

[12]Carroll T L.Chaotic systems that are robust to added noise[J].Chaos，2005，15(1):1－7.

[13]Shi Z，Qiao S，Chen K S.Ambiguity functions of direct chaotic radar employing microwave chaotic Colpitts oscillator[J].Progress In Electromagnetics Research，2007，77:1－14.

[14]Alonge F，Branciforte M，Motta F.A novel method of distance measurement based on pulse position modulation and synchronization of chaotic signals using ultrasonic radar systems[J].IEEE Transactions on Instrument and Measurement，2009，58(2):318－329.

[15]Lidong L，Jinfeng H，Zishu H.Chaotic signal reconstruction with application to noise radar system[J].EURASIP Journal on Advances in Signal Processing，2011，1(2):1－8.

[16]Lidong L，Jinfeng H，Zishu H.A Robust Controller for Synchronization of Chaotic System[J].Journal of Optoelectronics and Advanced Materials，2011，13(4):354－358.

[17]刘嘉兴，文吉.Ka频段混沌扩频测控系统的设想[J].电讯技术，2009，49(5):33－37.LIU Jia－ xing，WEN Ji.Conception for a Ka－ band chaotic spread spectrum TT＆C system[J].Telecommunication Engineering，2009，49(5):33－ 37.(in Chinese)

[18]Travassos X L，Vieira D，Palade V，et al.Noise Reduction in a Non－Homogenous Ground Penetrating Radar Problem by Multiobjective Neural Networks[J].IEEE Transactions on Magnetics，2009，45(5):1454－1457.