基于统计可信度的压缩感知协作频谱检测算法*
2014-09-28李娜,陈松,李鸥
李 娜,陈 松,李 鸥
(1.信息工程大学 信息系统工程学院,郑州450001;2.信息工程大学导航与空天目标工程学院,郑州450001)
1 引言
认知无线电(Cognitive Radio,CR)的概念起源于1999年Joseph Mitolo博士的奠基性工作,其核心思想是CR具有学习能力,能与周围环境交互信息,以感知和利用在该空间的可用频谱,并限制和降低冲突的发生。FCC在一份调查报告中的测量显示,授权频谱的时空利用率在15% ~85%之间[1]。根据文献[2]统计结果,小于3 GHz的频谱在空间时间上的平均使用率低于5%。CR正是利用了频谱利用率低这一特点,在不影响主用户(Primary User,PU)前提下,认知用户(Cognitive User,CU)利用频谱空穴,提高频谱利用率。因为CU对空闲频谱的使用对于PU是透明的,因此空闲频谱的感知是CR的基础。频谱检测范围越宽,能够检测的频谱的空闲概率也就越大,频谱利用率可灵活性也就越高,但是随着频谱带宽的增加,检测器件的成本和复杂度也呈几何式地增加。如何在较低的成本下实现宽频谱的检测一直以来都是研究的重点。
压缩感知(Compressed Sensing,CS)[3]技术作为宽频谱检测的方法之一,近年来受到了广泛的研究。CS与传统的Nyquist定理最大的不同在于:它直接从全局上去探究信号的本质结构与内容,不是局部地测量信号的物理表征量,脱离了与信号的具体物理测度(如频率之间的联系)[4]。Tian等人在文献[5]中,将CS理论引入宽带认知无线电系统,并利用小波变换进行感知频谱的边缘检测。文献[6]利用了模拟/信息转换器(Analog-to-Information Converter,AIC)进行宽带模拟信号的信息获取,最后通过检测频谱的能量,判定频谱占用情况。文献[7]则给出了一种多滤波器组的方式进行信道能量观测,通过直接检测信道能量降低了系统的复杂度。
认知无线电系统中,单点检测无法从根本上解决隐终端和阴影遮蔽等问题,而要更好地减轻这两个问题对于频谱检测造成的影响就需要引入多点的协作频谱检测[8]。协作频谱检测可分为硬决策和软决策两类决策算法[9]。硬决策的协作频谱检测算法主要包括“AND”和“OR”等。“AND”算法指所有协作认知用户均检测到授权用户的信号时,才判定授权用户使用频带;“OR”算法指任意一个协作用户检测到授权用户的信号,就判定为授权用户使用频带。软决策是指认知用户每次检测时估计认知用户接受信噪比或其他检测参量给中心单元,中心单元根据贝叶斯、奈曼-皮尔逊或最大后验概率等准则进行判决[10]。硬决策方法下,每个CU仅将检测到信道的有无情况反馈到认知中心,此种方式相当于对信道进行了“0或1”的重建,此种方法在减小控制信道的开销的同时也损失了信道的其他相关信息。软判决方法则将信号的所有特征信息传回认知中心,其代价则是占用了大量的控制信道。
文献[11]研究了认知无线电系统中的协同能量检测算法的性能,主要讨论了信噪比、协作用户数以及检测概率之间的关系,提出的SSAMP算法有效降低了算法的复杂度,但是其调节步长的确定需要进一步的研究。文献[12]针对认知无线电中协作频谱感知机制进行了优化,给出了检测周期、检测时间和搜索时间的选取和优化方法,并提出了新的信道搜索方式。上述文献主要针对协作检测的机制和策略进行了研究,但是如何将压缩感知应用于协作频谱检测,并更好发挥两者的优势,将是一个非常值得研究的课题。
2 系统模型
2.1 压缩感知
设离散信号x∈RN为一个N×1向量,x在N×N维正交基 Ψ=[ψ1,ψ2,…,ψN]下是 K-稀疏的,并且K<<N,即
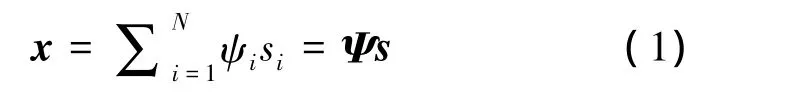
其中,稀疏系数向量s只包含K个非零元素。用观测矩阵Φ∈RM×N对x进行线性观测。测量矩阵需要满足约束等距性(Restricted Isometry Property,RIP)[13],并且观测矩阵 Φ 与基矩阵 Ψ 尽量不相干。其原因在于对信号进行观测时,尽量使每次的观测值包含有原始信号的不同信息成分。本文中观测矩阵Φ选取零均值高斯矩阵。
接收端包含加性噪声n的观测值y:
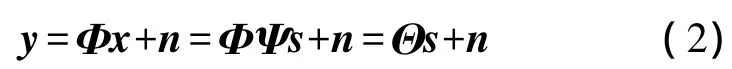
其中,Θ=ΦΨ是一个M×N的压缩感知矩阵,根据压缩感知理论,仅需M次线性观测就能以极大概率精确重构出原信号 x[3]:

再通过求解l1范数下的优化问题可得出稀疏向量s的近似估计值:

解决式(4)的最优化问题,可以使用基追踪方法进行求解,常用的有凸优化方法和匹配追踪方法。其中经典的凸优化算法有 BP-Simplex、BP-Interior[14]、线性规划(Linear Programming,LP)[7]、基追踪(Basis Pursuit,BP)[13]。常用的匹配追踪算法有匹配追踪(Matching Pursuit,MP)[15]、正交匹配追踪(Orthogonal Matching Pursuit,OMP)[16]、正则正交匹配追踪 (Regularized Orthogonal Matching Pursuit,ROMP)算法[17]、压缩采样匹配追踪(Compressive Sampling Matching Pursuit,CoSaMP)算法[18]、稀疏自适应匹配追踪(Sparsity Adaptive Matching Pursuit,SAMP)算法[19]等。其中,OMP算法作为最早的贪婪迭代算法之一,其思想具有典型性。该算法在重构时,每次迭代后都对已选择的原子集合进行正交化,保证了迭代的最优性,并减少了迭代的次数。
2.2 协作频谱感知模型
本文考虑存在认知中心的协作感知场景,具体场景如图1所示。假设网络中有1个PU用户,共有J个CU用户,CU用户通信时单位信道带宽为B,PU所在通信网络的总带宽为W,则信道总数为N=W/B。如果采用传统方式进行宽带频谱感知,每个CU都需要采样率大于等于2W的ADC,工程实现中往往需要达到3~4W。在W较大的情况下,CU的复杂度和成本都将呈现几何式的增长。

图1 协作频谱检测场景图Fig.1 The scene of cooperative spectrum detection
本文采用压缩感知的方法,每个CU独立生成M×N的高斯随机矩阵Φj(j=1,2,…,J)作为测量矩阵,对整个W频宽的信号xj(t)(j=1,2,…,J)进行线性测量。其中M满足取独立高斯同分布的矩阵[20]。
3 基于统计可信度的协作频谱检测算法
3.1 算法思想
协作频谱感知算法中,硬判决算法占用传输信道资源少,但是需要CU对接收的信号进行分析预处理,增加了CU的复杂性;软判决算法回传信息丰富,但是需要的传输信道资源多。
压缩感知的方法中,CU的每个线性测量都包含了原始信号的所有信息,CU可以选择不做任何处理,直接将检测到的M×1维向量回传至认知中心,也可选择对检测到的信号进行预处理,将预处理后的信息传回认知中心进行综合处理。假设yj为第j个CU接收到的信号:

其中,nj为加性噪声。
如果CU选择将Hj直接回传至认知中心,由认知中心对Hj分别使用OMP算法,得到拥有K个非零元素的K×1维向量以及对应的N×1维的正交基Ψ索引向量。假设Ψ使用的是傅里叶正交基,则中非零元素的分布代表了第j个CU所接收到信号的频谱功率分布情况。如yj采用12比特量化,则每个CU回传的数据量为

如果CU能够拥有一定的处理能力,可以由CU对自己的检测数据进行解算重构,并且仅回传重构后的以及非零元素在中的位置索引,由认知中心进行综合处理。假设采用12比特量化的位置索引使用8 b,则回传数据量为
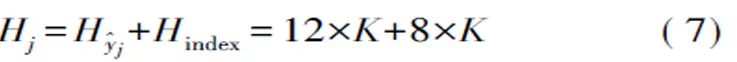
不同的CU在PU的范围内的分布不同,其检测PU所发信号的环境和特点也是不同的,CU如果所处的信道环境好,对于PU所发信号检测的正确概率也更高,反之则拥有较低的检测概率。在信道缓变的情况下,可以根据CU的历史检测概率给予其不同的判决权重,由此提高最终检测正确率。认知中心对CU回传信息设定的可信度为ωj:
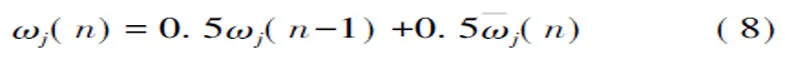

其中
(n)为认知中心根据 ω
1…J
(n-1)得到的第 n 次检测结果
(n)为用户第n次检测的结果。认知中心将获得的索引向量
与可信度ω
j
加权求和,得到Y(n):
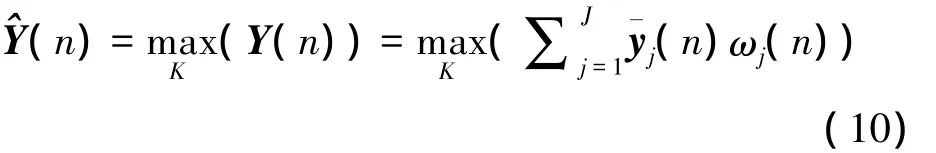
3.2 算法流程
初始化:生成J个观测矩阵Φj,索引集=,残差rj=yj,迭代次数n=1,用户可信度ωj=1。取最大列向量更新到索引集中,并将T中对应列向量置零。,得到的j为最小二乘意义上的最佳解。Step4:判断n≥2K,否,则跳转Step1继续循环;是,则跳转Setp5。
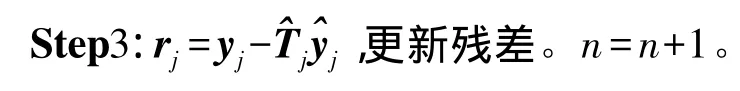
Step5:根据 ωj(n-1)得到
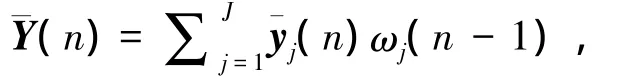
再根据

更新ωj(n)。
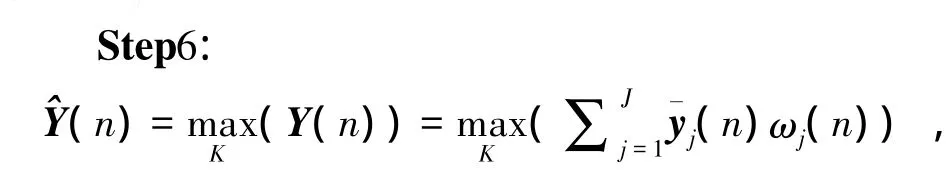
4 仿真与结果比较分析
本文利用Matlab平台进行仿真实验,针对多用户协作感知中用户数目、用户检测信噪比分布范围、检测概率、线性测量数M之间的关系进行仿真分析。为方便计算,假设N=256,随机选取8个信道被PU占用,其余信道为空闲信道。仿真信道为AWGN信道。信噪比范围SNRrange表示的是用户的信噪比随机波动的范围。其中“算术平均法”是认知中心将CU的感知结果直接算术求和。“统计可信度”方法即为本文介绍的方法。每项实验都独立运行1 000次。
图2显示了在 SNRrange∈[-20,20](dB)时,线性采样数M取不同数值的情况下,认知用户数与检测概率的关系。从图中可以看出,使用统计可信度方法的检测概率都要略高于传统的算术平均方法。在用户数较多的情况下,系统获得的多用户分集增益高,两种方法都能够以很大的概率正确检测到频谱的占用情况;而在用户数较少的情况下,统计可信度方法的检测概率比算术平均法约高出10%。
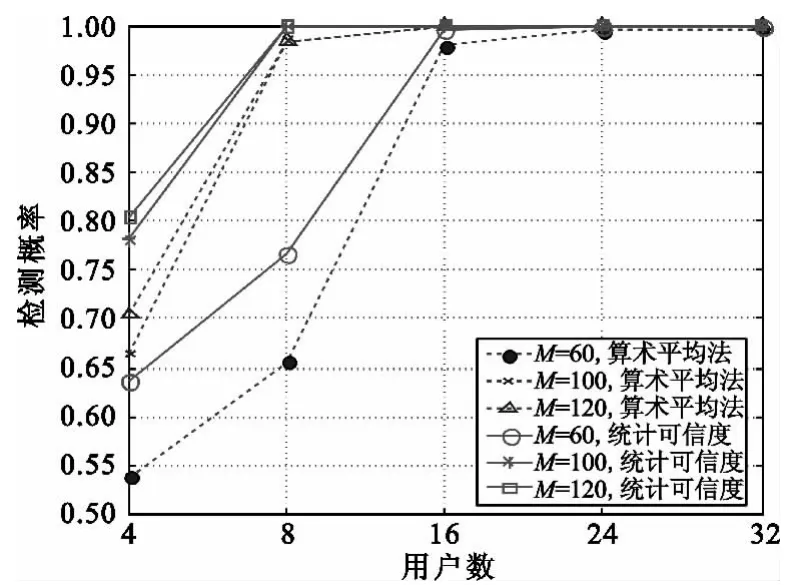
图2 不同M值下用户数与检测概率的关系Fig.2 The relation between the number of users and detection probability in the condition of different M
图3 显示了在 SNRrange∈[-20,20](dB)时,M取值与检测概率的变化关系。从图中可以看出,在用户数较少(如用户数为8)的情况下,统计可信度方法能够比算术平均法提高约10%的检测率;在用户数较多的情况下,也能够获得3% ~5%的检测率提升。

图3 M取值与检测概率的关系Fig.3 The relation between M and detection probability
从图2和图3可以看出,用户数较少时,统计可信度的方法效果更好,其主要原因在于用户数较少,多用户分集增益少,此时统计正确率高的用户也意味着有着较好的检测环境,此时给予其更大的判断权重,能够有效地提高最终的检测概率。
图4显示了在用户数为16时,在不同信噪比范围下,M取值与检测概率的关系。从图中可以看出,信噪比变化范围越大,用户的检测概率越高,并且统计可信度的方法较之算术平均法能够获得更高的检测准确率。

图4 不同信噪比范围下M取值与检测概率的关系Fig.4 The relation between M and detection probability in the condition of different SNR range
图5 显示了M=40时,在不同信噪比范围下,用户数与检测概率的关系。从图中可以看出,随着用户数量的增多,统计可信度方法较之算术平均法获得的增益愈发增大。这是因为用户数较多时,信噪比变化范围增大后,部分高信噪比用户能够得到很高的检测概率,由此整体提高了系统的频谱检测性能。

图5 不同信噪比范围下用户数与检测概率的关系Fig.5 The relation between the number of users and detection probability in the condition ofdifferent SNR range
5 结束语
认知无线网络中为了更好地利用空闲频谱,频谱感知经常需要对较宽的频谱进行检测分析。压缩感知方法是一种将高维稀疏量映射到低维空间进行观测的方法,同时,协作感知机制能够更好地解决频谱检测中的隐终端和阴影遮蔽的问题,降低漏检和误检概率。综合以上考虑,本文给出了基于统计可信度的压缩感知协作频谱检测算法,该算法通过压缩感知方法实现宽频谱的检测,降低了用户与认知中心的交互信息量;同时,利用了协作感知中认知用户的统计可信度,对用户的压缩感知结果加权判断,进一步提高了频谱检测概率。仿真结果表明,本算法对比于直接算术平均的方法,可以进一步提高频谱检测概率,提升了频谱检测的性能。
[1]FCC.ET Docket No 03-222 Notice of Proposed Rule Making and Order[R].Washington,DC:FCC,2003.
[2]Kolodzy P.Dynamic Spectrum Policies:Promises and Chalenges[C]//Proceedings of the 4th Annal Digital Broadband Migration Symposium.[S.l.]:CommLaw Conspectus,2004:147-159.
[3]Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[4]张雄伟,黄建军,朱涛.压缩感知新技术专题讲座(一)[J].军事通信技术,2011,32(4):83-87.ZHANG Xiong-wei,HUANG Jian-jun,ZHU Tao.Special Lecture in Compressed Sensing Technology(1)[J].Military Communications Technology,2011,32(4):83-87.(in Chinese)
[5]Tian Z,Giannakis G B.Compressed sensing for wideband cognitive radios[C]//Proceedings of 2007 International Conference on Acoustics,Speech,and Signal Processing.Honolulu,HI,USA:IEEE,2007:1357-1360.
[6]Polo Y L,Wang Y,Pandharipande A,et al.Compressive wide-band spectrum sensing[C]//Proceedings of 2009 International Conference on Acoustics,Speech,and Signal Processing.San Diego,CA,USA:IEEE,2009:178-183.
[7]Havary-Nassab V,Hassan S,Valaee S.Compressive detection for wide-band spectrum sensing[C]//Proceedings of 2010 International Conference on Acoustics,Speech,and signal Processing.Dallas,TX,USA:IEEE,2010:3094-3097.
[8]Quan Zhi,Cui Shuguang,Poor H V,et al.Collaborative Wideband Sensing for Cognitive Radios[J].IEEE Signal Processing Magazine,2008,25(6):60-73.
[9]Yueek T,Arslan H.A Survey of Spectrum Sensing and Algorithms for Cognitive Radio Applications[J].IEEE Communication Survey & Tutorials,2009,11(1):116-130.
[10]肖林,刘凯.认知无线电网络中的最佳可信度频谱检测算法[J].西安电子科技大学学报(自然科学版),2011,38(5):79-84.XIAO Lin,LIU Kai.Optimal Credibility Spectrum Sensing Algorithm in Cognitive Radio Networks[J].Journal of Xidian University(Natural Science),2011,38(5):79-84.(in Chinese)
[11]虞贵财,罗涛,乐光新.认知无线电系统中协同能量检测算法的性能研究[J].电子与信息学报,2009,31(11):2682-2686.YU Gui-cai,LUO Tao,YUE Guang-xin.Energy Detection Algorithm Investigation Based on Cooperative in Cognitive Radio Systems[J].Journal of Electronics& Information Technology,2009,31(11):2682-2686.(in Chinese)
[12]郭晨,彭涛,王文博.认知无线电网络中合作频谱感知机制的优化[J].电子与信息学报,2009,31(7):1525-1530.GUO Chen,PENG Tao,WANG Wen-bo.Optimization of Cooperative Spectrum Sensing Mechanisms in Cognitive Radio Networks[J].Journal of Electronics & Information Technology,2009,31(7):1525-1530.(in Chinese)
[13]Candes E,Tao T.Decoding by linear programming[J].IEEE Transactions on Information Theory,2005,51(12):4203-4215.
[14]陈宝林.最优化理论与算法[M].3版.北京:清华大学出版社,2005:37-196.CHEN Bao-lin.Optimizing Theory and Algorithm[M].3rd ed.Beijing:Tsinghua University Press,2005:37-196.(in Chinese)
[15]Davis G,Mallat S,Avellaneda M.Adaptive greedy approximations[J].Constructive Approximation,1997,13(1):57-98.
[16]Tropp J A,Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666.
[17]Needell D,Vershynin R.Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J].Foundations of Computational Mathematics,2007,9(3):317-334.
[18]Needell D,Tropp J A .CoSaMP:Iterative signal recovery from incomplete and inaccurate samples[J].Application Computational Harmon Analog,2009,26(3):301-321.
[19]Do T T,Lu Gan,Nam N,et al.Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]//Proceedings of the 42nd Asilomar Conference on Signal,Systems and Computers.Pacific Grove,USA:IEEE,2008:581-587.
[20]于向楠,郑宝玉,见春雨.基于PN编码器的压缩感知超宽带信道估计[J].南京邮电大学学报(自然科学版),2012,32(3):51-55.YU Xiang-nan,ZHENG Bao-yu,JIAN Chun-yu.UWB Channel Estimation Based on PN-encoder Filter Compressive Sensing[J].Journal of Nanjing University of Posts and Telecommunications(Natural Science),2012,32(3):51-55.(in Chinese)
