毫米波信道中波束成形矢量的波束宽度

2022-12-08楼斌剑王海泉黄怡李紫薇俞芸芸

电信科学 2022年11期

楼斌剑，王海泉，黄怡，李紫薇，俞芸芸

毫米波信道中波束成形矢量的波束宽度

楼斌剑，王海泉，黄怡，李紫薇，俞芸芸

（杭州电子科技大学，浙江杭州 310018）

波束成形矢量技术能够集中所发送的能量于某一指定区域，从而提高系统性能，是5G的核心技术之一。但正是由于能量被集中这一特点，信道的任何变化都可能会使接收方越出此特定区域，从而使系统的鲁棒性能降低。波束成形矢量的波束宽度这一概念就是衡量这对矛盾的指标之一。已有的波束宽度大多针对天线而言，并非针对波束成形矢量。针对波束成形矢量，借助格拉斯曼流形中的概念，给出并研究了波束宽度的定义，在此基础上，探讨了拓宽波束宽度的方法。研究发现，天线数越多，能量越能够集中，但波束宽度受限，从而鲁棒性越弱。

毫米波；波束成形；波束宽度；格拉斯曼流形；波束拓宽

0 引言

随着无线通信技术的发展，无线电频谱的低频段趋于饱和，毫米波的高频段因可以提供充裕带宽而受到广泛关注，但是由于其波长短、对材料的穿透性差，相较于低频段的传输，其路径损耗严重。为了解决上述问题，毫米波通信通常采用大型的天线阵列以及波束成形矢量技术，把有限的能量覆盖到指定的区域，以对抗较大的路径损失[1-3]。但是，如果波束变窄，用户或目标的微小变化就会使用户或目标离开波束覆盖区域，导致波束的鲁棒性变差；另一方面，如果波束变宽，则有限的能量就被分散，从而降低了系统性能。所以，宽波束和高辐射功率就是一对矛盾。例如，在高铁场景下，接收端的高速移动需要频繁地切换波束，利用宽波束可以在一定程度上降低切换的频率，从而降低系统的复杂度，但在边缘区域，宽波束的辐射功率通常不满足通信要求，这就需要利用窄波束对抗较大的路径损失；在设计预编码码本时，波束覆盖有效区域的大小也是系统的性能指标之一。当覆盖相同的区域时，若波束宽度较宽，则码本中的码字个数相对少，对波束的管理就较为方便，但同时波束增益较小；若波束宽度较窄，则码字的个数就要增加，波束管理就更为复杂，但波束增益较高。

为了权衡上述两者之间的关系，需要研究波束宽度及寻找控制拓宽波束的方法。为此首先需要研究的是波束宽度的定义。从文献[4-6]看，存在两种波束宽度的定义：第一种是针对天线阵列提出的波束宽度的概念；第二种是针对波束成形矢量提出的概念。显然第一种概念针对系统的硬件，而第二种针对系统的软件[4-5]。对比两者可知，第一种定义没有考虑实际传输过程中天线数量以及毫米波信道特性带来的影响，而第二种定义与天线数量以及毫米波信道特性紧密相关。本文针对第二种定义展开讨论。

其次，需要研究波束拓宽的方法。目前的波束拓宽方法大多基于第一种定义讨论，常用的方法是通过添加额外的射频开关关闭部分天线，从而减少子阵列规模[6]，但这种方法工程实现困难，并且降低了阵元的利用率，使得天线的发射增益下降。文献[7]利用一个功率增强型的水平宽波束以及个垂直波束结合，获得了与7波束接近的覆盖性能，其中={0,1,2,3}，但没有具体指出如何得到宽波束。文献[8]针对硬件添加了反射镜给出加宽的波束。文献[9-13]都利用调整相位的方法拓宽波束。文献[9]通过翻转部分子阵列的权值使得波束宽度可以自由拓宽，而不受振幅控制，也不损失功率。文献[10]假设每个单元阵列的天线相位都是可以独立调整的，这对于连续均匀子阵列来说是不现实的。文献[11]提出了一种有效的连续均匀子阵列波束拓宽方法，用3种改进的迭代傅里叶变化和一种遗传算法求解波束的最佳扩展模式。文献[12]提出了一种基于两步最小二乘法的阵列合成算法，该算法利用阵列天线相位的随机性设计天线阵列。文献[13]提出了一种非迭代的纯相位波束拓宽方法，该方法依赖于线性阵列和平面阵列的二次相位激励模式。

基于第二种波束宽度定义的工作比较少见。文献[6]针对阵列响应矢量提出了基于虚拟子阵列合成的波束拓宽的方法，而文献[14]针对特定的波束成形矢量，将波束拓宽问题表述为非线性优化问题，在满足功率约束条件的前提下，利用序列二次规划（sequence quadratic programming，SQP）技术搜寻最佳波束，使得传输功率阵列因子最大，但上述工作中提到的波束成形矢量都是限定在特定形式下的波束成形矢量。文献[15]针对任意形式的波束成形矢量，给出了约束结构，在满足约束条件的情况下对形成波束的控制参数进行数值穷举，使得增益最大。但是它仅仅考虑了信道中只有一个入射角的情形，没有考虑毫米波信道中多个入射角带来的影响，且波束宽度定义为半功率波束宽度（half-power beamwidth，HPBW），即与主光束峰值相比，辐射图幅度减小3 dB的角度跨度，显然这种定义不够灵活，只能计算半功率时的波束宽度。

综上所述，有必要针对任意的毫米波信道及任意的功率利用率重新定义波束成形矢量的波束宽度。首先，基于任意波束功率利用率的概念给出了单个路径下波束宽度的定义，并给出了理论上界；其次，构造了新的、具有更宽波束宽度的波束成形矢量，并讨论了常用的及新构造的波束成形矢量的性质；最后，把上述结果推广到任意毫米波信道的情况，给出了多个路径下波束宽度的定义及具体计算过程，同样也讨论了常用的波束成形矢量在多径条件下的性质。

1 单路径下的波束宽度

假设信道路径为单路径。

在大规模天线系统中，通常利用波束成形技术聚集所发送信号的能量，消除路径损耗。显然，波束越窄，所发送的能量就越集中，这样就越有利于信号的传送，但是，信道的微小变化就会带来波束的抖动，因此，波束越窄，鲁棒性就越差。为了权衡高增益与强鲁棒性，本文引入波束宽度这一指标描述两者之间的关系。为此有必要先介绍格拉斯曼流形以及格拉斯曼距离的相关概念。

1.1 格拉斯曼流形与格拉斯曼距离

(,)中的元素有多种表示方法，本文采用维矩阵表示，即对于一个的满秩矩阵，它的列向量所生成的子空间，记为[]，表示(,)中的元素。显然对于任意的满秩方阵，的列向量所生成的空间与的列向量所生成的空间相同，因此，[]= []，即在(,)中，它们表示同一个元素。

假设1和2是两个维数为的满秩矩阵，且它们的奇异值分解为：

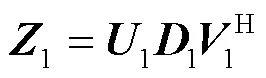
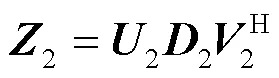
其中，为的酉矩阵，为的对角矩阵，为的酉矩阵，= 1,2。显然，[]= []，且的列向量是[]的一个标准正交基。下面定义[1]与[2]之间的格拉斯曼距离。

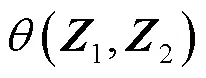
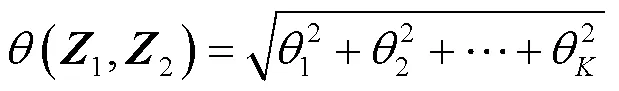
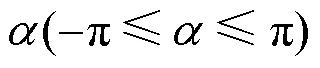
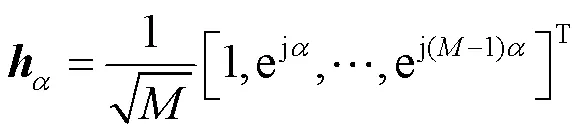
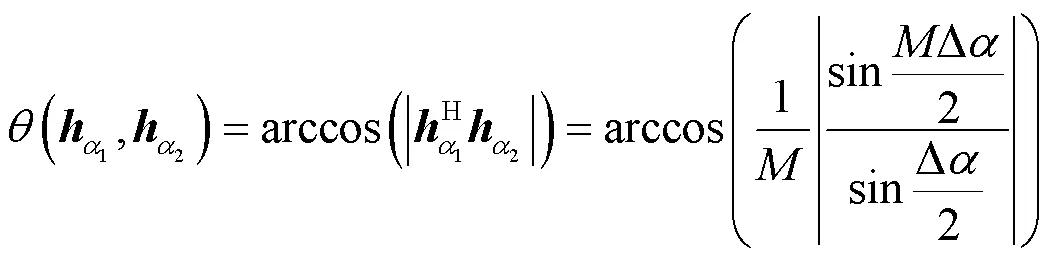
因此，(1,2)∈[0, π/2]。当∆= 0时，(1,2) = 0，当∆= 2π/（≠0）时，(1,2) = π/2，达到最大值。由此可知，当∆从0增加到2π时，(1,2)从0增加到π/2。另外，当增大时，格拉斯曼距离(1,2)的变化幅度增大。∆与格拉斯曼距离的关系如图1所示。

图1 ∆α与格拉斯曼距离的关系

1.2 波束宽度的定义及性质

假设基站配备均匀线性阵列（uniform linear array，ULA），且阵元数为，为阵元的间距，则波束成形矢量可以表示为：

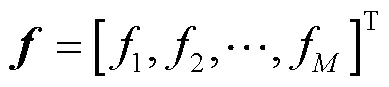
以下定义的波束宽度。

本节只考虑一个主路径，其阵列响应矢量为：

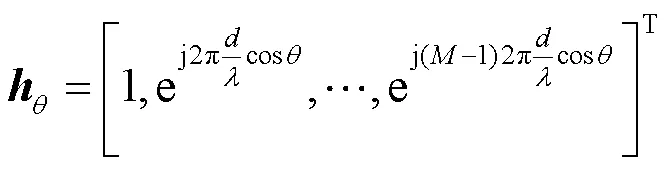
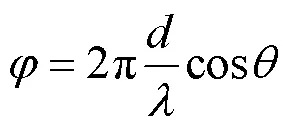
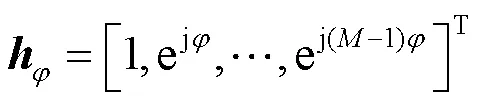
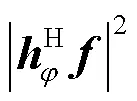
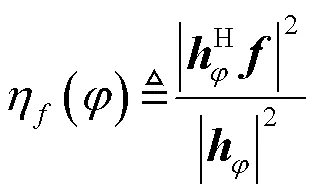
接下来给出波束宽度的定义。不同于常用的半功率波束宽度，本文根据利用率给出一种新的定义，具体定义如下。

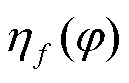
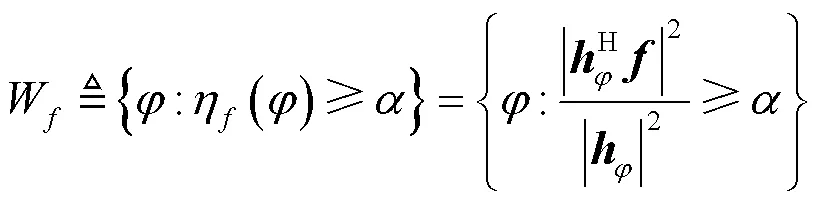
其中，为给定常数，且∈[0,1]，则波束宽度B()定义为波束区域的长度。

以上定义是针对波束成形矢量给出的，有别于天线理论中波束宽度的概念。显然，对于固定的，B()是的减函数，即最小利用率增大，波束宽度减小，当= 05时，就相当于常用的半功率波束宽度。由此可知，以上定义比常见的半功率波束宽度这一概念更加灵活。

如果W是一个连续区间，则有：

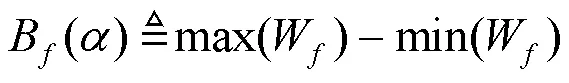
例如，假设波束成形矢量为阵列响应矢量，可以表示为：

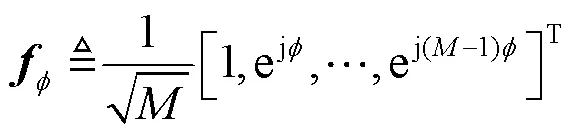
其中，为波束指定的方向。式（9）中的信道矢量的利用率为：

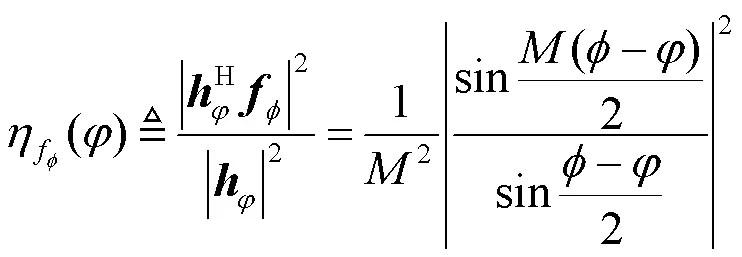
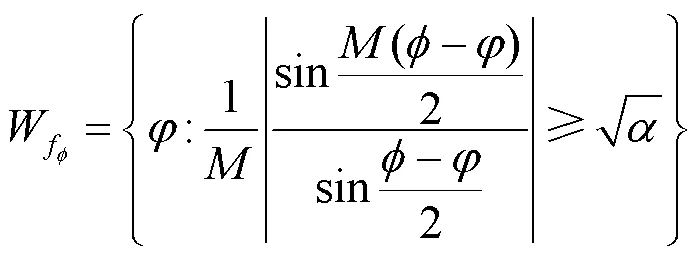
为了方便描述，定义函数：

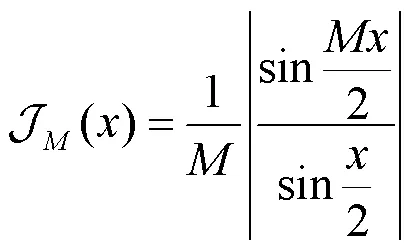
则式（15）可以表示为：

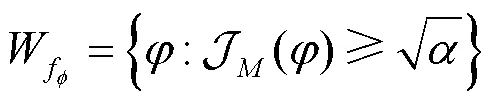
例如，取= 07，当= 32时，其波束宽度为0.127 0 rad（1 rad=180°/π）；当= 64时，其波束宽度为0.063 5 rad；而当= 128时，其波束宽度为0.031 7 rad；由此可见，当天线数增加一倍时，波束宽度大约减少一半。

下面给出波束宽度的几个上界。为此，需要讨论波束宽度与格拉斯曼距离之间的关系。假设是阵列响应矢量（如式（13）所示），则由式（6）、式（16）和式（18）可得：

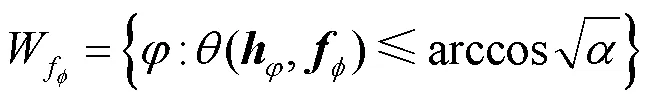
对于一般的波束成形矢量及给定的常数，利用傅里叶变换可以证明波束宽度满足以下的上界。

定理1 对于任意的波束成形矢量及任意的常数，波束宽度B()满足以下不等式。

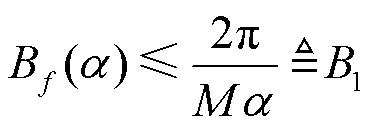
证明如下。

式（22）可以改写为：

从而有：

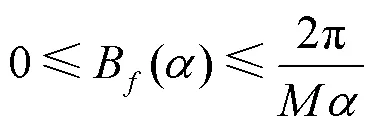
证毕。

由此可见，对于给定的，当天线数增加时，波束宽度线性地减少。例如，取= 07，当= 32时，由计算可得，1= 0280 4 rad；当= 64时，1= 0140 2 rad；而当= 128时，1= 0070 1 rad。上界1还有很大的改进空间。事实上，利用格拉斯曼流形中距离的定义（如第1.1节所示），可以得到更紧致的上界。

定理2 对于任意的波束成形矢量及任意的常数(05)，波束宽度B()满足以下不等式。

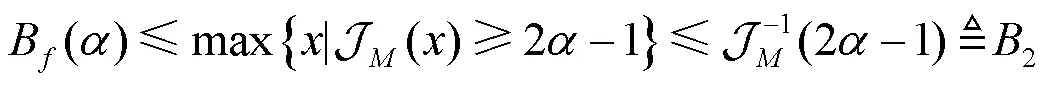
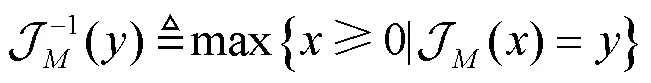
等价地，信道矢量与波束成形矢量之间的格拉斯曼距离(,)满足以下条件。

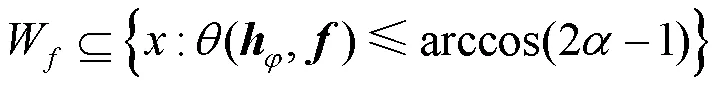
证明如下。

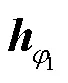
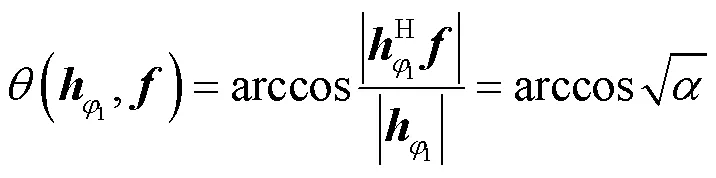
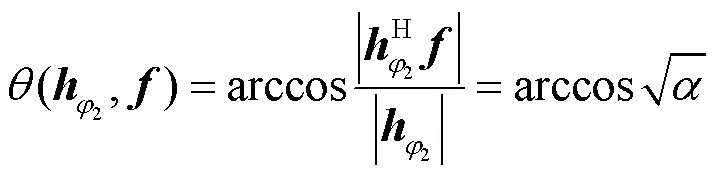
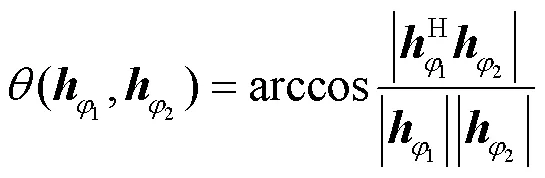
根据式（16），可以将式（31）简化为：

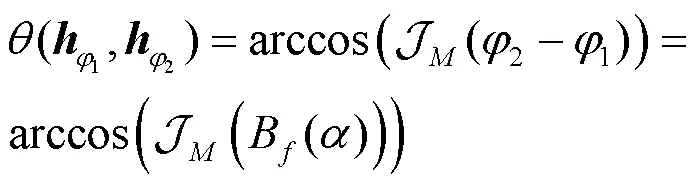
根据三角形两边之和大于第三边的性质，可以得到如下关系。

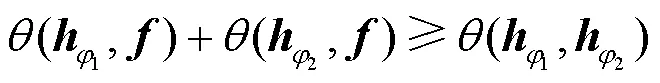
因而有：

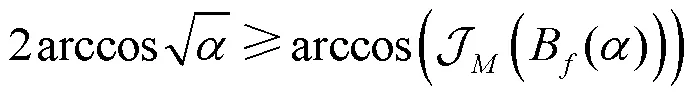
所以：

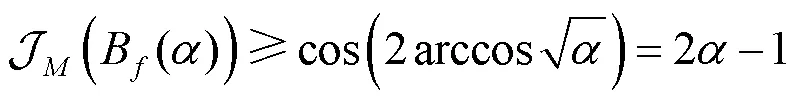
故：

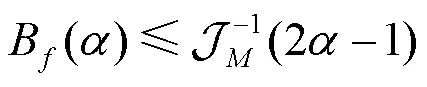
证毕。

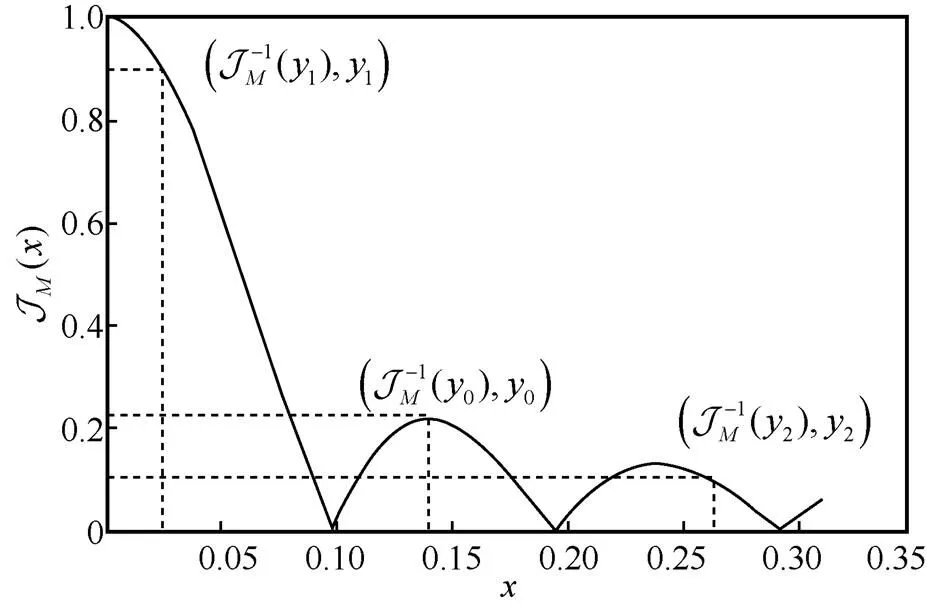
图2 函数曲线

例如，= 07，当= 32时，由计算可得上界2= 0139 2 rad；当= 64时，2= 0066 4 rad；而当= 128时，2= 0033 2 rad。与上界1相比，上界2更加紧致。

1.3 几类特殊波束的波束宽度

1.3.1 阵列响应矢量的波束宽度

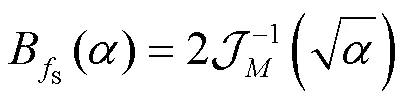
正如前面所指出的，阵列响应矢量作为波束可以达到最大的利用率，但是其波束宽度与波束宽度的上界有较大的差距，因此，希望构造出具有更宽的波束宽度的波束成形矢量。

1.3.2 由理想低通滤波器构造的波束成形矢量

由定理1的证明可知，假设()为理想低通滤波器，其通带长度为2π则通过傅里叶反变换可以得到波束成形矢量的第个分量为：

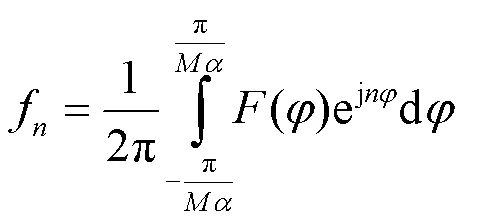
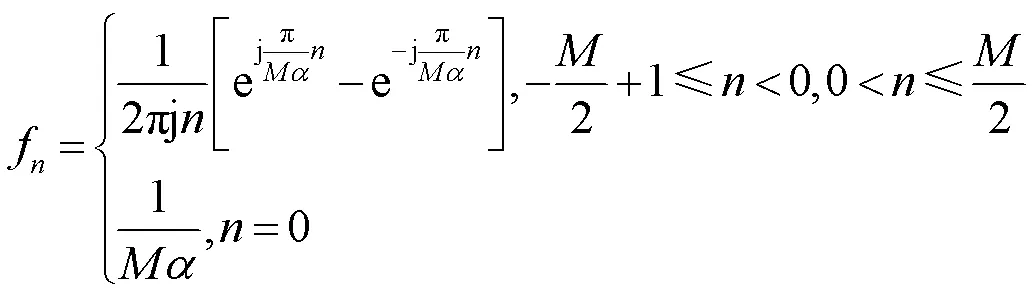
例如，取= 07，当= 32时，由计算可得，其波束宽度为0.131 6 rad，最大利用率为0.933 6；当= 64时，其波束宽度为0.065 8 rad，最大利用率0.933 9；而当= 128时，其波束宽度为0.032 9 rad，最大利用率为0.934 0。由此可见，这种波束成形矢量通过降低最大利用率换取波束宽度的增加。

1.3.3波束

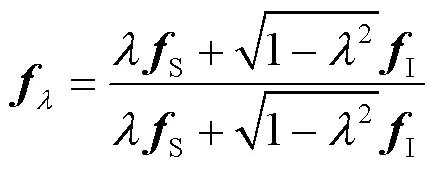
图3 λ波束的利用率与信道方向φ的关系

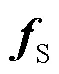
由表1可知，当固定时，随着天线数量的增加，波束宽度逐渐减少，故在实际应用中，基站的天线并不是越多越好，天线越多意味着波束更窄，鲁棒性变差，一旦用户稍微移动一段距离，利用率便快速下降，导致通信质量很差，而波束可以通过选取不同的值权衡最大利用率与波束宽度的关系。

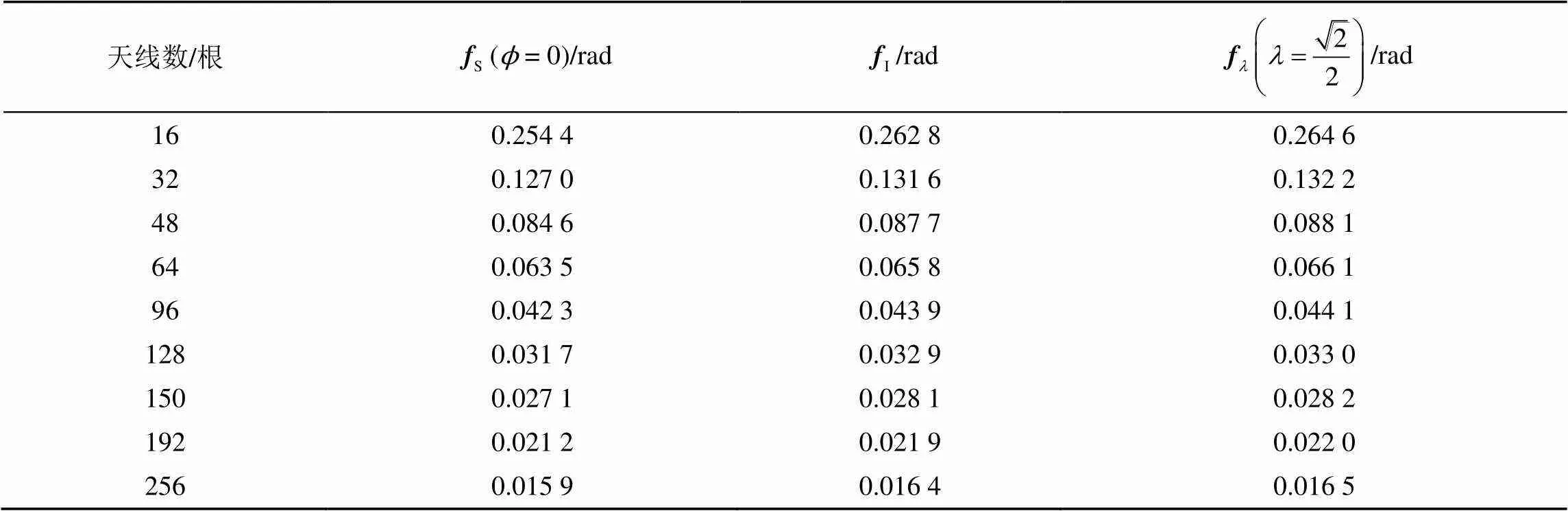
表1 3种波束的波束宽度

2 多路径下的波束宽度

2.1 波束宽度的定义

在实际通信过程中，通常不会只存在一个路径，因此，有必要讨论多路径下的波束宽度的定义及其性质。

假设基站配备阵元数为的均匀线性阵列，路径数为，那么信道向量可以表示为：

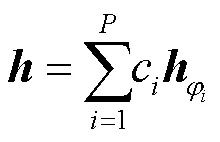
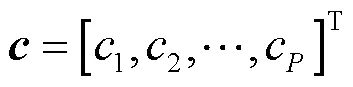
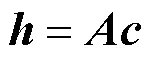
由此可知，信道向量包含在由的列向量所生成的空间[]中。下面讨论波束宽度的定义。

由第1节可知，在多径的环境中，对于给定的波束成形矢量及给定的常数，波束区域W仍然可以表示成以下形式。

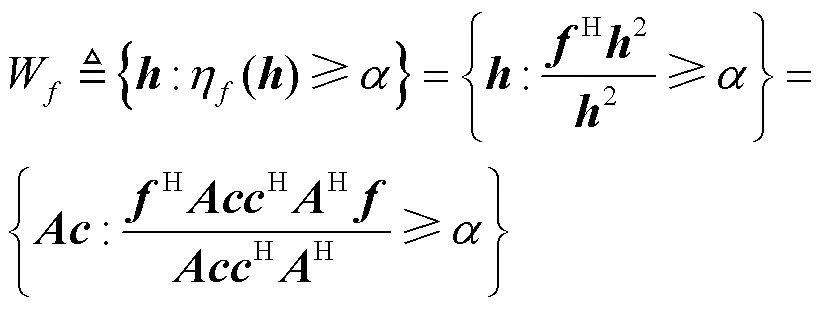
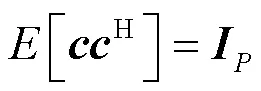
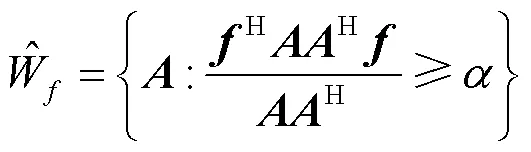
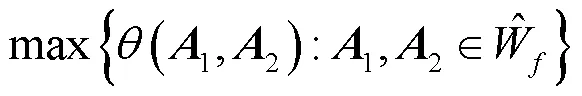
但由于这个最大值与维数有关，而在实际情况中是一个随机变量，因此，求平均得到：

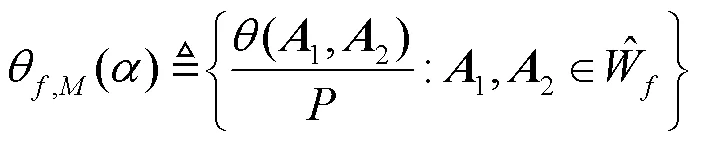
根据式（27）可以给出如下定义。

定义3 对于任意的波束成形矢量及任意

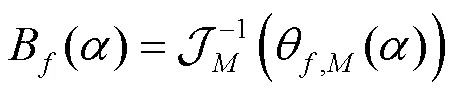
采取上述定义的理由如下。

（1）希望得到一个与路径数无关、统一的定义。

（2）第1节波束宽度的定义过程如下：先给出利用率的定义（如式（10所示）），这是讨论波束宽度的出发点，再根据此定义给出了波束区域的定义（如式（11）所示），最后给出了波束宽度的定义。但在多个路径的场合，波束区域是多维空间中的一个子集，无法采用一个指标衡量一个区域的大小。因此采用格拉斯曼流形中的距离的概念。从式（13）～式（18）得到启发，采用这些步骤，就有了上述定义。

（3）从仿真效果来看（如图4所示），上述定义基本达到要求，即波束宽度基本与无关。

（4）显然，当= 1且为阵列响应矢量时，上述定义与第1节中的波束宽度的定义完全一致。

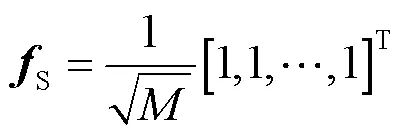
图4 不同路径数下天线数与阵列响应矢量的波束宽度的关系

2.2 几类特殊波束

2.2.1 阵列响应矢量的波束宽度

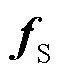
表2 的波束宽度与天线数关系

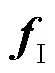
表3 的波束宽度与天线数关系

2.2.2 由理想低通滤波器构造的波束

3 结束语

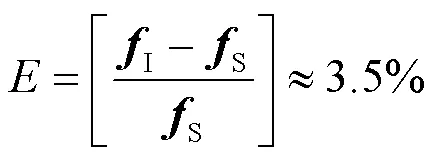
[1] XIAO M, MUMTAZS, HUANG Y M, et al. Millimeter wave communications for future mobile networks[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(9): 1909-1935.

[2] HEMADEH I A, SATYANARAYANA K, EL-HAJJAR M, et al. Millimeter-wave communications: physical channel models, design considerations, antenna constructions, and link-budget[J]. IEEE Communications Surveys & Tutorials, 2018, 20(2): 870-913.

[3] 何世文, 黄永明, 王海明, 等. 毫米波无线通信发展趋势及技术挑战[J]. 电信科学, 2017, 33(6): 11-20.

HE S W, HUANG Y M, WANG H M, et al. Development trend and technological challenges of millimeter-wave wireless communication[J]. Telecommunications Science, 2017, 33(6): 11-20.

[4] 赵珈琪. 高铁通信中面向波束切换的波束成形方法研究[D]. 南京: 南京邮电大学, 2021.

ZHAO J Q. Research on beamforming methods for beam switching in high speed railway communications[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2021.

[5] 谢坚筱. 面向毫米波无线通信的波束成形关键技术研究[D]. 北京: 北京邮电大学, 2020.

XIE J Y. Research of key technologies of beamforming for millimeter wave wireless communication[D]. Beijing: Beijing University of Posts and Telecommunications, 2020.

[6] 张仁民. 毫米波通信系统多分辨率码本设计与低开销波束训练技术研究[D]. 南京: 东南大学, 2019.

ZHANG R M. Multi-resolution codebook design and low-overhead beam training for millimeter-wave communications[D]. Nanjing: Southeast University, 2019.

[7] 李贝, 胡煜华, 王鑫炎, 等. 5G网络SSB 1+X波束技术应用研究[J]. 电信科学, 2022, 38(1): 150-158.

LI B, HU Y H, WANG X Y, et al. Research on SSB 1+X beam technology of 5G network[J]. Telecommunications Science, 2022, 38(1): 150-158.

[8] CALLAGHANP, YOUNG P R. Beam-and band-width broadening of intelligent reflecting surfaces using elliptical phase distribution[J]. IEEE Transactions on Antennas and Propagation, 2022, PP(99): 1.

[9] RAJAGOPAL S. Beam broadening for phased antenna arrays using multi-beam sub arrays[C]//Proceedings of 2012 IEEE International Conference on Communications. Piscataway: IEEE Press, 2012: 3637-3642.

[10] KERCE J C, BROWN G C, MITCHELL M A. Phase-only transmit beam broadening for improved radar search performance[C]//Proceedings of 2007 IEEE Radar Conference. Piscataway: IEEE Press, 2007: 451-456.

[11] DANIEL B K, ANDERSON A L. Phase-only beam broadening of contiguous uniform sub arrayed arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(5): 4001-4013.

[12] ZENG X N, ZHANG Y S, HE F, et al. Practical beam broadening for space-borne SAR using phase-only pattern synthesis[C]//Proceedings of 2011 International Conference on Wireless Communications and Signal Processing (WCSP). Piscataway: IEEE Press, 2011: 1-4.

[13] FONTENEAU C, CRUSSIÈRE M, JAHAN B. A systematic beam broadening method for large phased arrays[C]//Proceedings of 2021 Joint European Conference on Networks and Communications & 6G Summit (EuCNC/6G Summit). Piscataway: IEEE Press, 2021: 7-12.

[14] ELSHAFIY A, SAMPATH A. Beam broadening for 5G millimeter wave systems[C]//Proceedings of 2019 IEEE Wireless Communications and Networking Conference. Piscataway: IEEE Press, 2019: 1-6.

[15] RAGHAVAN V, CEZANNEJ, SUBRAMANIANS, et al. Beamforming tradeoffs for initial UE discovery in millimeter-wave MIMO systems[J]. IEEE Journal of Selected Topics in Signal Processing, 2016, 10(3): 543-559.

Beamwidth of beamforming vectors in millimeter-wave channels

LOU Binjian, WANG Haiquan, HUANG Yi, LI Ziwei, YU Yunyun

Hangzhou Dianzi University, Hangzhou 310018, China

The beamforming technology is one of the core technologies in 5G and it can concentrate the transmitted energy in a specified area, thereby improving the performance of the system. But it is because of this feature that the energy is concentrated，any changes of the channel may cause to keep the receiver outside the specified area, and therefore, the performance of robustness is reduced. The concept of the beam width of a beamforming is one of the indicators to measure this tradeoff. Existing definition of beam widths are based on antennas, not on beamforming. Interms of beamforming, the definition of beam width was given and studied with the help of the concept in Grassmannian manifolds. On this basis, the method of beam width was discussed. It is found that the beam width of beamforming is closely related to the number of the transmitting antennas. The more the number of antennas, the more concentrated the energy, and the weaker robustness is.

millimeter wave, beamforming, beam width, Grassmannian manifold, beam broadening

TN91

10.11959/j.issn.1000–0801.2022288

2022–04–21；

2022–11–10