SiCP/6061Al复合材料高温单轴拉伸时相关棘轮行为的细观本构模型

郭素娟，康国政，张 娟，轩福贞

（1.华东理工大学机械与动力工程学院承压系统与安全教育部重点实验室，上海 200237；2.西南交通大学力学与工程学院，成都 610031）

0 引 言

颗粒增强金属基复合材料（PRMMCs）具有密度小、强度高、热稳定性好、制造成本低和宏观各向同性等特点，已广泛用于汽车、航空航天、军工和体育用品等行业，如汽车的活塞和气缸、制动件、飞机前缘加筋板、轻质装甲和高尔夫球杆头等。在这些应用中，复合材料件通常要承受复杂的循环载荷作用，而且很多时候还要处于高温、高压的工作环境下，其在承担非对称应力循环加载时，会产生塑性变形的累积现象，即棘轮行为。棘轮行为可导致结构疲劳寿命降低，或者使其塑性变形超限而无法正常使用，这是颗粒增强金属基复合材料在工程应用中必须要考虑的重要问题之一。为了更好地对复合材料结构件的强度、疲劳寿命和可靠性进行评价，必须对该类复合材料在室温和高温下的循环变形行为（特别是棘轮行为）有充分的认识，并能做出合理的理论描述。

目前，国际上关于颗粒增强金属基复合材料循环变形行为的研究主要集中在试验研究和细观循环本构描述两个方面。在试验研究方面，学术界已经通过应变循环的宏、微观试验，对不同合金基体的颗粒增强复合材料的循环硬化/软化特性以及循环变形的微观机理进行了较系统的研究［1－2］。此外，文献［3］对承受常应力的金属基复合材料在温度循环载荷下的棘轮行为进行了研究；文献［4］对SiCP/6061Al复合材料进行了系统的室温和高温单轴试验研究，分析了颗粒体积分数、加载历史和各种时相关因素对复合材料棘轮行为的影响。在细观循环本构描述方面，研究者已通过平均场均匀化理论［5－8］建立了一系列的细观弹/粘塑性循环本构模型，对颗粒增强金属基复合材料在单轴应变循环加载下的时无关和时相关循环变形行为进行了合理的描述。目前针对复合材料棘轮行为的本构研究还不多，Guo等［9］在Eshelby等效夹杂理论的基础上，对基体材料引入了能够合理描述其棘轮行为的非线性随动硬化律，合理描述了SiCP/6061Al复合材料在室温下的时无关棘轮行为；并基于统一粘塑性框架，对Mori-Tanaka均匀化理论进行了粘塑性推广［10］，采用广义增量仿射线性化方法建立了基于应力加载的细观粘塑性循环本构模型，该模型对SiCP/6061Al复合材料在室温下的时相关棘轮行为进行了较为合理的描述，但其在高温下棘轮行为（特别是在保持时间较长和应力水平较高时）的模拟结果却远低于试验值。为此，作者在文献［10］的细观本构框架下，在非线性随动硬化律中引入了反映热恢复效应的修正项，得到了一个新的细观粘塑性循环本构模型；同时，通过与试验结果的比较，验证了模型对复合材料高温棘轮行为的预测能力。

1 细观粘塑性循环本构模型

文献［10］所提出的细观粘塑性循环本构模型（简称UVP模型）主要是基于统一粘塑性本构框架建立的，其对复合材料棘轮效应的描述主要通过基体材料的非线性随动硬化演化律来体现。然而，由于该模型发展的修正Abdel-Karim-Ohno非线性随动硬化演化律并没有考虑复合材料在高温下的热恢复效应，因而无法合理描述SiCP/6061Al复合材料在高温下的时相关棘轮行为。因此，作者在非线性随动硬化律中引入能反映热恢复效应的修正项［11］对UVP模型进行拓展，发展了一个新的细观粘塑性循环本构模型（简称UVPT模型）。以下将主要简述UVPT模型的主要框架。

1.1 Mori-Tanaka均匀化模型的推广

主要利用式（1）（广义仿射线性化方法）对复合材料各相（基体相和颗粒相）的粘塑性本构方程进行线性化，进而对适合应力加载的Mori-Tanaka均匀化模型［9］进行粘塑性推广［10］。

推广所得的粘塑性 Mori-Tanaka均匀化表达式可以表述如下：

式中：0表示基体相；1表示颗粒相；v1为颗粒的体积分数；［ Δσn＋1］i和 （）i分别为颗粒（i＝1）或基体（i＝0）的平均应力增量和放射应变增量；I为四阶单位张量；，分别为复合材料所承担的宏观应力、应变增量；〈·〉表示求体积平均；A′和Dnal＋g1分别为应力集中张量和一致性柔度矩阵，可通过式（5～9）求得：

1.2 基体材料的循环本构模型

对于SiCP/6061Al复合材料来说，其增强相陶瓷颗粒非常坚硬，因此它的塑性变形主要由基体合金引发。这里视SiC颗粒为弹性材料，即有（Δ）1＝0，（C）1＝ （C）1。对 于 基 体 材料，主要对文献［10］中引入的统一粘塑性本构模型进行修正，在新发展的非线性随动硬化律中加入反映热恢复效应的修正项，具体主控方程可参见文献［10］，修正后的背应力演化方程可表述如下：

式中：αi（i＝1，2，…M）为α的分量。

取μ＝μ0exp（kp）来描述试验中观察到的基体材料棘轮应变率随循环周次减小的特性，其中μ0为初始棘轮参数，p为累积塑性应变，k为演化系数，ri、ζi可按照文献［11］的方法通过基体的单轴拉伸曲线来确定；χ和m可根据单轴或多轴棘轮试验结果通过试错法来确定。

1.3 基体材料一致性切线刚度矩阵的推导

由1.1节的均匀化表达式可知，一致性切线刚度矩阵在复合材料的细观粘塑性循环本构模型中起着至关重要的作用。由于视SiC为弹性材料，因此其一致性切线刚度矩阵可直接取弹性刚度矩阵。而对于基体材料，加入热恢复项对其本构模型进行修正之后，需要重新推导相应的粘塑性一致性切线刚度矩阵。为了避免较小的时间步长所引起的矩阵奇异性，文献［10］对粘塑性一致性切线刚度矩阵进行了规则化处理，所得规则化表达式为：

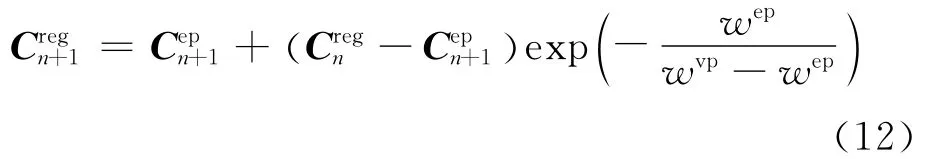
沿用式（12）所示的规则化表达式，针对修正之后的粘塑性本构模型，分别推导Cepn＋1，wep和wvp，可得：

式中：R′（pn＋1）为对反映各向同性硬化的函数R（pn＋1）取微分；Cel为弹性刚度矩阵；G 为剪切模量；Nn＋1为塑性流动方向。

不考虑各向同性硬化时，取R（pn＋1）＝0。Ln＋1和Ui等未给出物理含义的变量均为公式推导过程中形成的变量表达式。

以上各量满足如下方程：

2 模拟结果和讨论

基于新发展的复合材料细观粘塑性循环本构模型（UVPT模型），对SiCP/6061Al复合材料在高温（300℃）下的时相关单轴拉伸和棘轮行为进行了数值模拟，在模拟中考虑了加载速率和峰值保持时间等时相关因素对复合材料棘轮行为的影响。为了突出UVPT模型的优势，将文献［10］中UVP细观本构模型得到的模拟结果以及相应的试验研究曲线在下文中一并给出。

2.1 复合材料组元的材料特性

模拟过程中SiC颗粒被视为弹性材料，其弹性模量EP为460GPa，泊松比ν为0.25；假定界面为理想界面，6061铝合金基体材料为满足1.2节介绍的非线性随动硬化模型的粘塑性材料。相关的材料参数可通过高温下基体材料的单轴拉伸曲线按文献［11］中的方法获得。其中，控制棘轮演化的参数μ0和k可根据复合材料的一条棘轮演化曲线通过试错法获得。高温（300℃）下基体材料的材料常数如下：M＝10，Em＝57.5GPa，ν＝0.33，Q0＝90MPa，K＝150，n＝4.5，μ0＝1.0，k＝380，χ＝3.2，m＝1×10－7，ξ（1）＝3 843，ξ（2）＝1 774，ξ（3）＝1102，ξ（4）＝625，ξ（5）＝250，ξ（6）＝100，ξ（7）＝50，ξ（8）＝25，ξ（9）＝14.3，ξ（10）＝8.3，r（1）＝60.04MPa，r（2）＝18.8MPa，r（3）＝16.1MPa，r（4）＝7.1MPa，r（5）＝10.2MPa，r（6）＝2.4MPa，r（7）＝4.5MPa，r（8）＝2.7MPa，r（9）＝3.8MPa，r（10）＝3.3MPa

2.2 复合材料高温下单轴拉伸和棘轮行为

利用上述材料参数，首先采用不同细观循环本构模型（UVPT和UVP模型）对SiCP/6061Al复合材料及6061铝合金基体在高温（300℃）下的时相关单轴拉伸行为进行了模拟。从图1，2中可以看出，基体和复合材料的单轴拉伸行为在高温下表现出了明显的时相关特性，UVP模型和UVPT模型对6061铝合金基体及其复合材料单轴拉伸应力－应变曲线模拟得很好，由于在确定材料参数时已经考虑了UVPT模型中的热恢复修正项在应变加载下产生的应力松弛，因此UVPT模型对单轴拉伸曲线的模拟结果与UVP模型的几乎相同。

图1 6061铝合金基体在变应变速率加载下单轴拉伸应力－应变曲线的模拟结果和试验结果Fig.1 Simulated and experimental results of uniaxial drawing stress-strain curves of 6061aluminum alloy matrix at varied strain rate

考虑不同加载速率和保持时间的影响，预测了SiCP/6061Al复合材料在高温（300℃）下的单轴时相关棘轮行为。图3对应的加载工况为（90±140）MPa（30周），应力速率为3.5MPa·s－1，峰值保持时间分别为60，15，0s。图4对应的加载工况为（45±215）MPa（30周），无峰值保持时间。

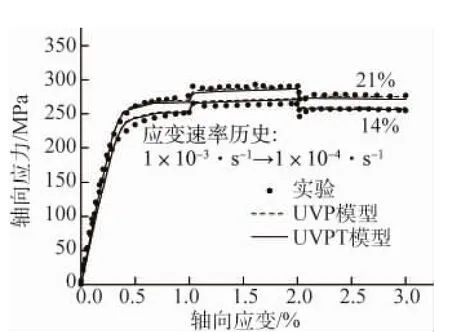
图2 颗粒体积分数为14%和21%的复合材料在变应变速率加载下单轴拉伸应力－应变曲线的模拟结果和试验结果Fig.2 Simulated and experimental results of uniaxial drawing stress-strain curves of the composite with particles of 14vol%and 21vol%at varied strain rate

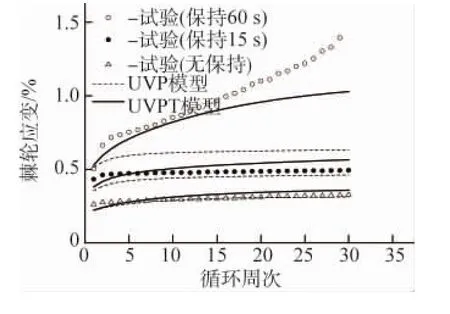
图3 颗粒体积分数为14%的复合材料在不同峰值保持时间下的单轴棘轮行为的模拟结果和试验结果Fig.3 Simulated and experimental results of uniaxial ratcheting of the composites with particles of 14vol%at different peak hold times

图4 颗粒体积分数为21%的复合材料在不同应力速率下单轴棘轮行为的模拟结果和试验结果Fig.4 Simulated and experimental results of uniaxial ratcheting of the composites with particles of 21vol%at different stress rates

从图3和图4中可以看出，在较低的应力水平和较短的保持时间下，UVP模型对复合材料的单轴棘轮行为模拟得较好，但在蠕变变形占主导因素的较长保持时间和较高应力水平下，其对复合材料单轴棘轮行为的模拟欠佳；UVPT模型由于同时考虑了材料的粘性流动以及在高温下的热恢复效应，从而对高、低应力水平和长、短保持时间下复合材料的单轴棘轮行为均得到了较为合理的预测。可见，在基体材料的非线性随动硬化演化律中引入热恢复项，能有效提高模型对复合材料高温拉伸时相关棘轮行为的预测能力。此外，所建立的细观粘塑性循环本构模型并未考虑复合材料内部由于循环变形和高温交互作用引起的微结构损伤。在今后的研究工作中，很有必要考虑界面损伤对复合材料循环变形的影响，建立考虑界面结合状态的细观循环本构模型。

3 结 论

（1）在已有试验研究和细观本构模型的基础上，在新发展的非线性随动硬化律中引入反映热恢复效应的修正项，并重新推导了一致性切线刚度矩阵，得到了一个新的细观粘塑性循环本构模型（简称UVPT模型）。

（2）与 UVP模 型 相 比，UVPT 模 型 能 为SiCP/6061Al复合材料在高温（300℃）下的时相关单轴棘轮行为进行更为合理的描述。

［1］LLORCA J.Fatigue of particle-and whisker-reinforced metalmatrix composites［J］.Progress in Materials Science，2002，47：283-353.

［2］POZA P，LLORCA J.Mechanical behavior of Al-Li/SiC composites-Part II：cyclic deformation tests［J］.Metall Mater Trans：A，1999，30：857-867.

［3］ZHANG H，DAEHN G S，WAGONER R H.The temperature-cycling deformation of particle reinforced metal matrix composites：a finite element study［J］.Scripta Metallurgica et Materialia，1990，24：2151-2155.

［4］KANG G Z. Uniaxial time-dependent ratcheting of SiCP/6061Al alloy composites at room and high temperature［J］.Composites Science and Technology，2006，66：1418-1430.

［5］DOGHRI I，OUAAR A.Homogenization of two-phase elasto

plastic composite materials and structures study of tangent operators，cyclic plasticity and numerical algorithms［J］.International Journal of Solids and Structures，2003，40：1681-1712.

［6］DOGHRI I，FRIEBEL C.Effective elasto-plastic properties of inclusion-reinforced composites：study of shape，orientation and cyclic response［J］.Mechanics of Materials，2005，37：45-68.

［7］DOGHRI I，ADAML，BILGER N.Mean-field homogenization of elasto-viscoplastic composites based on a general incrementally affine linearization method［J］.International Journal of Plasticity，2010，26：219-238.

［8］MERCIER S，MOLINARI A.Homogenization of elastic-viscoplastic heterogeneous materials：self-consistent and Mori–Tanaka schemes［J］.International Journal of Plasticity，2009，25：1024-1048.

［9］GUO S J，KANG G Z，ZHANG J.Meso-mechanical constitutive model for ratchetting of particle-reinforced metal matrix composites［J］.International Journal of Plasticity，2011，27：1896-1915.

［10］GUO S J，KANG G Z，ZHANG J.A cyclic visco-plastic constitutive model for time-dependent ratchetting of particle-reinforced metal matrix composites［J］.International Journal of Plasticity，2013，40：101-125.

［11］KAN Q H，KANG G Z，ZHANG J.Uniaxial time-depen dent ratchetting：visco-plastic model and finite element application［J］.Theoretical and Applied Fracture Mechanics，2007，47：

133-144.