藕状多孔铜凝固界面前沿溶质场的数值模拟

戴希魁，金青林，蒋业华，周 荣

（昆明理工大学材料科学与工程学院，昆明 650093）

0 引 言

1993年，乌克兰学者Shapovalov提出了一种利用金属/气体共晶定向凝固制备多孔金属的新技术［1］，称为Gasar工艺。由于采用该工艺制备的多孔金属的结构类似藕根，因此也被称为藕状多孔金属材料［2］。相比于传统多孔金属材料，这种藕状多孔金属材料表现出了优异的特性，如小的应力集中、良好的导热能力以及较高的力学性能等［3－4］，同时具有比相同致密度材料更高的综合力学性能，如更高的比模量、比强度。

现有文献对Gasar工艺中金属/气体两相共晶生长理论的研究报道较少。Liu等［5］虽然通过建立溶质场的三维模型确定了孔间距和凝固速率之间的共晶生长模型，但对溶质场的求解较复杂和冗长；Yamamura等［6］利用气孔内外溶质原子扩散的平衡关系，建立了压力和孔隙率关系的理论模型，但没有进一步讨论凝固速率对孔隙率的影响。基于此，作者建立了凝固界面前沿的溶质场，分析了工艺参数（氢气压力和凝固速率）对结构参数（孔隙率、孔间距）和溶质浓度的影响，并进行了试验验证。

1 试样制备与试验方法

材料制备在真空感应熔炼定向凝固装置［7］中进行。在高压氢气（纯度99.99%）气氛（压力分别为0.6，1.0MPa）中，通过电磁感应加热，在坩埚中熔炼铜（纯度99.99%），熔炼温度为1 573K，保温30min，使氢气充分溶入熔体中；之后，提起控制杆使坩埚中的熔体流入带有水循环冷却装置且侧面保温的铸型中，熔体进行自下而上的定向凝固。由于氢气在液相和固相铜中存在溶解度差，凝固界面处过饱和的氢气将析出，最终形成沿凝固方向排列于金属基体中的多孔结构，如图1所示。通过调节工艺参数（表1），可以得到不同结构参数的试样。

孔隙率利用Archimedes排水法进行测量；孔间距采用图像处理软件Image J多次测量后取平均值。

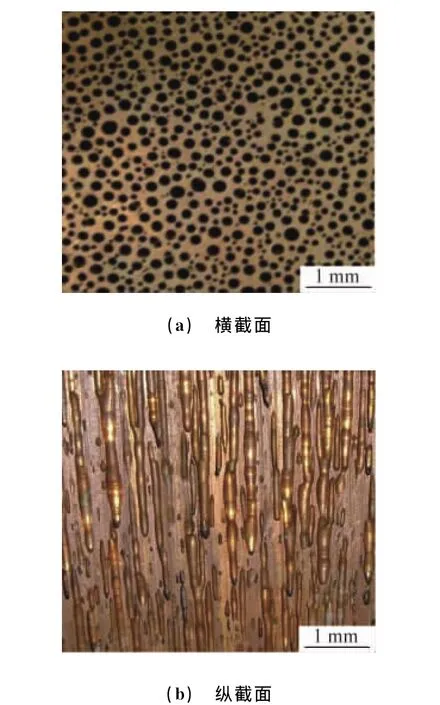
图1 藕状多孔铜的截面形貌Fig.1 Photographs of ordered porous copper：（a）transverse section and（b）longitudinal section

2 凝固界面前沿溶质场模型的建立

2.1 凝固界面前沿的溶质场

Gasar工艺的理论研究类似于规则共晶凝固，对溶质场的分析是基于传统经典的Jackson-Hunt模型［8］。为了简化模型分析，做出以下假设：（1）凝固以稳态形式进行；（2）凝固界面前沿无熔体对流；（3）孔径和孔间距（λ）均匀分布。

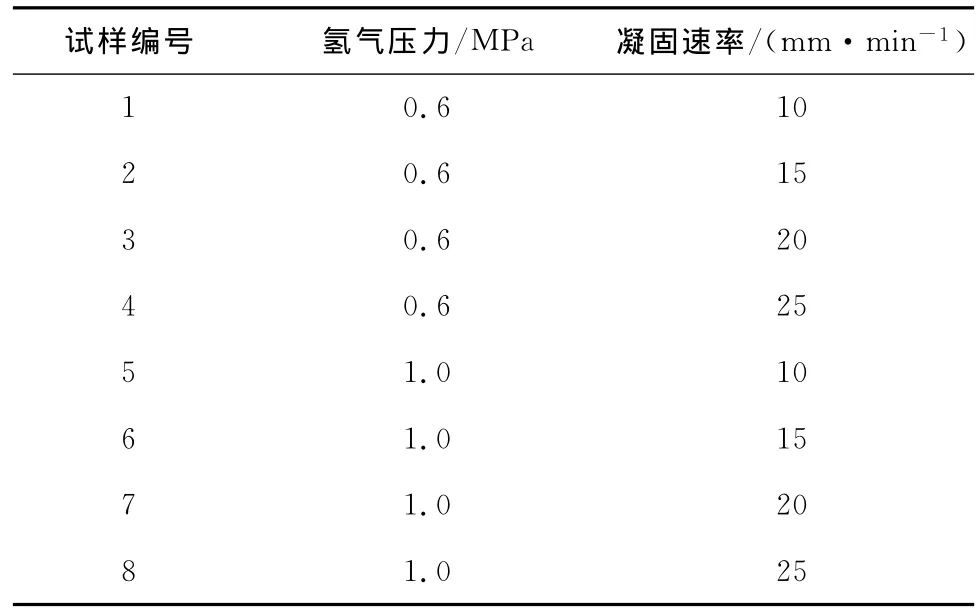
表1 试验工艺参数Tab.1 Process parameters

由于扩散的对称性，这里只考虑宽度为λ/2的一个区域。基于以上假设，建立凝固界面前沿溶质场的数学模型，如图2所示，其中ε为孔隙率。

图2 凝固界面前沿溶质场的示意Fig.2 The concentration field of solidification interface frontier

凝固界面前沿的溶质分布可用微分方程（1）描述，它描述了在沿凝固界面推进的方向上，凝固界面前沿溶质浓度和工艺参数之间的关系。

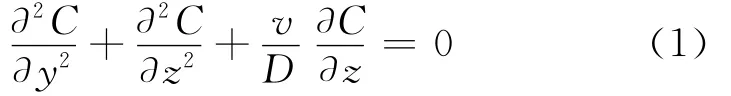
式中：C和D分别为溶质氢原子在液相中的浓度和扩散系数；z为凝固界面推进方向；y垂直于z；v为凝固速率。

经过数学求解可以得到式（1）的数学通解：

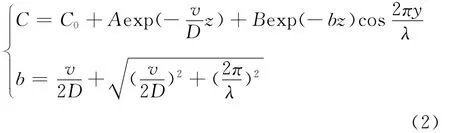
式中：C0为溶质氢原子在液相中的初始浓度，由Sievert定律确定；A，B，b均为常数，与工艺参数有关。

此通解由一个三角函数和一个指数函数构成。指数函数反映的是整个凝固界面的平面特性，三角函数反映的是固气相态在凝固界面的交替形态，也就是考虑了凝固界面受微扰动影响时的溶质分布，此微扰动通常是由温度起伏或不溶性固体颗粒引起的。在Gasar工艺中，由于凝固速率比较小，凝固界面生长属于低速生长。因此，对常数b有下列简化公式：

对于常数A，B的确定，则需要边界条件作以辅助。根据规则共晶的相关理论，凝固界面处的物质要遵循质量守恒原则，在达到稳态扩散时，由凝固排出的溶质量应等于界面处向液体内部扩散的溶质量，这样才能保证凝固界面以稳定的速率向前推进以及凝固界面前沿溶质的稳定扩散和转移。由此，可以得到凝固界面前沿固相、气相的边界条件：

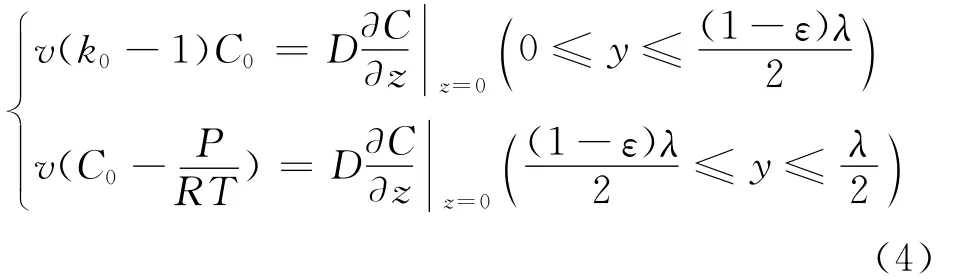
式中：k0为溶质平衡分配系数；ε为气相体积分数，即孔隙率；P为氢气压力；T为熔体温度；R为理想气体常数，R＝8.314J·（mol·K）－1。

在自变量y的范围内，对方程组（4）两边同时微积分，经过数学变换和化简可得：

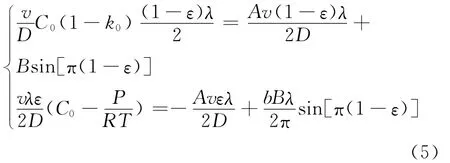
由方程组（5），可以确定系数A，B：

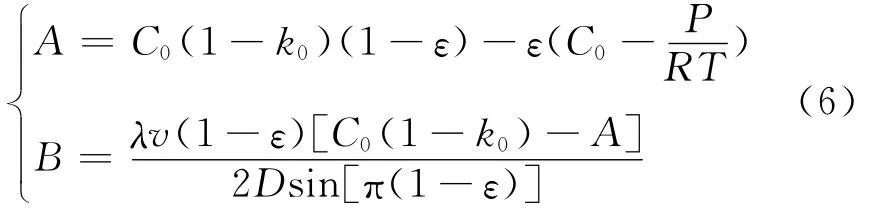
当z＝0时，式（2）可化简得：

由于在凝固界面存在如下关系：

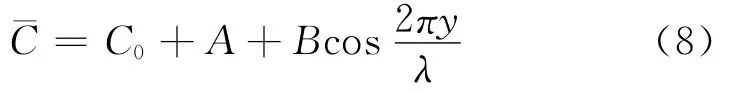
在设定的范围（λ/2）内，由式（7）和（8）可以求得：

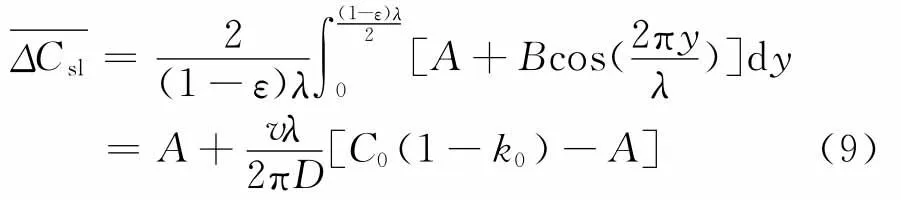
根据式（7）和（9），求得固液界面前沿溶质氢原子的平均浓度：

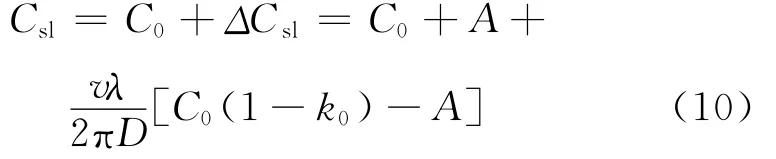
2.2 最小过冷度

在凝固界面处，根据凝固界面三相节点（图3）处的能量平衡关系，可以得出：

式中：σsl，σsg和σgl分别为固液、固气和气液间的界面能［9－10］，取值为0.256，1.605，1.360J·m－2；θs和θg是凝固界面三相交界处不同界面能之间的几何夹角。

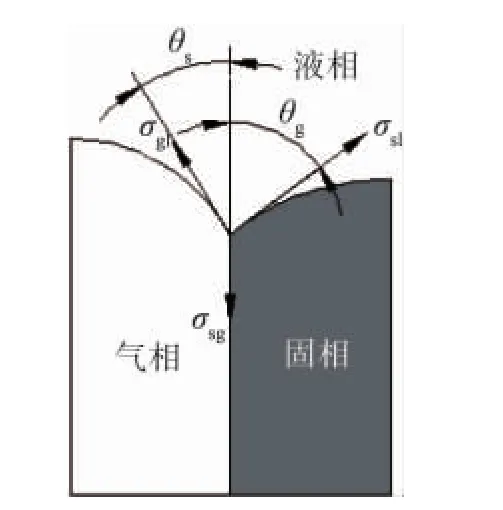
图3 凝固界面处不同界面间的关系Fig.3 The equilibrium relation of different interfacial energy in solidification interface

由方程组（11）可得：sinθg＝0.269 213；sinθs＝0.050 675。

由于凝固界面处于局部热力学平衡状态，所以体系溶质过冷度ΔTc和曲率过冷度ΔTr之和等于界面过冷度ΔT。故，可以得到凝固界面最小过冷度和孔间距之间的关系［8］：

式中：Kc和Kr为固气共晶的物理常数。

根据最小过冷度的判据原则，由选定的λ值可使ΔT达到最小值，即

由式（12）和（13）可得

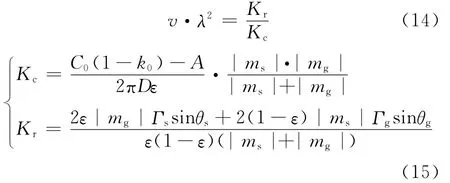
式中：ms和mg分别为固相和气相的液相线斜率；Γs和Γg分别为 固相和气 相 Gibbs-Thomson系数。

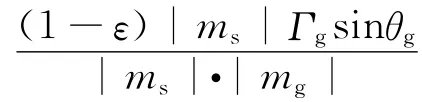
式（14）最终化简为

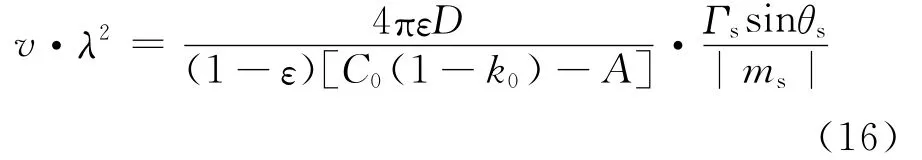
综上所述得：

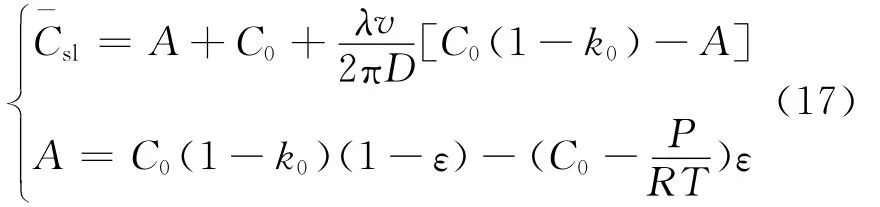
3 模型计算结果与分析

3.1 孔隙率的理论公式

不考虑氢气的溢出，文献［5］所得孔隙率的理论公式：

式中：Tm为铜的熔点；ρl和ρs分别为液相和固相铜的密度。

由式（17），（18）可知，保持压力和温度不变时，系数A和孔隙率ε均为常数，而扩散系数D在温度不变时也为常数。所以，孔间距（λ）和凝固速率（v）可以被描述为vλ2＝E（常数）的关系。

3.2 工艺参数对结构参数的影响

联立式（16），（17），（18），通过数值分析的方法可计算出工艺参数对结构参数的影响。计算参数［6，11－13］：C0＝0.808 2（PH2）1/2exp（－523 4/T）；D ＝ 0.512exp［－ 24 600/（RgT）］；Γs＝ 1.5 ×10－7mK；ms＝－ 0.010 26； k0＝0.35；Tm＝1 356K；ρs＝8.9 × 103kg· m－3；ρl＝ 8.0 ×103kg·m－3。将模型计算结果与试验结果进行对比，如图4所示，可见，两者吻合较好。

图4 不同压力下孔隙率和孔间距与凝固速率关系的模型计算结果与试验结果Fig.4 Calculated results and experimental results between porosity（a），（c）and inter-pore spacing（b），（d）with solidification rate under different pressures

由图4可以看出，保持氢气压力不变，随着凝固速率的增大，孔隙率和孔间距都逐渐减小，但孔隙率的变化不明显；保持凝固速率不变，随着压力的增大，孔间距和孔隙率均逐渐减小，且后者的变化明显。这表明孔隙率主要受压力的影响，而孔间距主要受凝固速率和压力的共同影响。在实际的定向凝固过程中，凝固界面前沿的液相中存在着熔体对流，对流会使溶质原子在液相中的扩散系数增大，结果造成实际的扩散系数大于理论扩散系数。而随着凝固速率或氢气压力的不断增大，凝固界面前沿熔体的对流程度也在加剧，造成了孔隙率计算结果和试验结果存在差距，但它们的变化趋势始终是一致的。

3.3 工艺参数对溶质浓度的影响

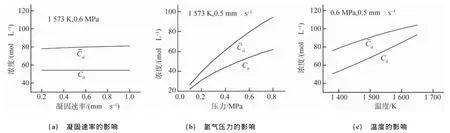
图5 不同工艺参数对固液界面前沿溶质浓度分布的影响Fig.5 Effects of process parameters on solute concentration distribution on solid-liquid interface frontier：（a）solidification rate；（b）pressure and（c）temperature

4 结 论

（1）建立的溶质场数学模型可以较准确地预测工艺参数和结构参数之间的关系；保持氢气压力和温度不变时，孔间距（λ）和凝固速率（v）呈vλ2＝E（常数）的关系。

（2）孔隙率主要受氢气压力的影响，孔间距主要受凝固速率和氢气压力的共同影响。

（3）随着凝固速率或氢气压力的增大，固液界面前沿溶质富集程度越来越大，并且压力对溶质富集程度的影响明显强于凝固速率的；随着温度的升高，溶质富集程度越来越小，这是由于随着温度的升高，熔体对流加快了溶质原子的扩散速率，从而在一定程度上削弱了溶质的富集。

［1］SHAPOVALOV V I.Method of manufacture of porous arti-cles：US，5181549［P］.1993-01-26.

［2］NAKAJIMA H.Fabrication，properties and application of porous metals with directional pores［J］.Progress in Materials Science，2007，52（7）：1091-1173.

［3］YUN S K，MURAKAMI K，NAKAJIMA H.Anisotropic mechanical properties of porous copper fabricated by unidirectional solidification［J］.Materials Science and Engineering：A，2001，299（1/2）：241-248.

［4］李言祥，刘源.金属/气体共晶定向凝固规则多孔金属的研究进展［J］.材料导报，2003，17（4）：1-4.

［5］LIU Yuan，LI Yan-xiang.A theoretical study of Gasarite eutectic growth［J］.Scripta Materialia，2003，49（5）：379-386.

［6］YAMAMURA S，SHIOTA H，MURAKAMI K，et al.Evaluation of porosity in porous copper fabricated by unidirectional solidification under pressurized hydrogen［J］.Materials Science and Engineering，2001，318（1/2）：137-143.

［7］黄峰，杨天武，李再久，等.规则多孔铜压缩性能的各向异性［J］.中国有色金属学报，2011，21（3）：604-610.

［8］KURZ W，FISHER D J.Fundamentale of solidfication［M］.Switzerland：Trans Tech Publications Ltd，1989：268-269.

［9］JONES H.The solid-liquid interracial energy of metals：calculations versus measurements［J］.Materials Letters，2002，53（4/5）：364-366.

［10］ALLEN B C.Liguid metals-chemistry and physics［M］.New York：Marcel Dekker，1972：161-168.

［11］张华伟，李言祥，刘源.Gasar工艺中金属－氢二元相图的研究［J］.金属学报，2005，41（1）：55-59.

［12］FISHER D J.Hydrogen diffusion in metalsl：a 30-year retrospective［M］.Switzerland：Scitee Publications Ltd，1999：1-173.

［13］安阁英.铸件形成理论［M］.北京：机械工业出版社，1989：173-174.