基于A-V模型的改进模型及单轴棘轮效应预测

陈小辉， 周 杨， 刘明月， 蔺永诚

(1.东北大学秦皇岛分校 控制工程学院, 河北 秦皇岛 066004； 2.中南大学 机电工程学院, 湖南 长沙 410083)

核反应堆、压力容器及管道、航空发动机、海上平台等结构/构件在复杂载荷服役及反复受载的状态中发生棘轮效应，即会导致材料持续产生循环塑性应变的累积.在实际工程中棘轮效应会降低结构/构件的疲劳寿命或引起结构/构件的大变形，影响正常工作.因此，国内外的一些设计规范中已要求对结构/构件的棘轮效应进行分析，如中国的JB4732—1995(2005年确认)，美国的ASME Code Section III，德国规范KTA和法国规范RCC-MR.

目前许多学者针对平均应力、应力幅值、加载率、加载历史以及应力比等多种加载方式对棘轮效应的影响进行了研究，利用循环本构模型对棘轮效应进行预测已经取得了非常大的进步，比如， Armstrong和Frederick(A-F)模型[1]是最经典的非线性随动硬化模型之一，它是通过引入一项动态恢复项从而改善了传统线性随动强化模型.利用A-F模型预测的材料棘轮效应高于试验值.文献[2-9]以A-F模型为基础对其进行了改进，改进模型可以不断增加参数量，但对棘轮效应的预测存在一定瑕疵.Bower[10]通过加上了一个与背应力相关的附加项及其演化方程改善了A-F 模型中的动态恢复项，该模型预测的材料棘轮效应仍然高于试验值.Ahmadzadeh等[11]在Bower模型的基础上引入参数δ解决了棘轮效应易于安定的问题，并研究了Al6061/SiCp复合材料在单级和阶梯加载条件下的棘轮变形，成功地预测了不同加载历史下的棘轮应变曲线[12].Karvan等[13]提出各向同性变量会显著影响A-V模型中变量b的大小，通过在A-V模型中加入不同的各向同性硬化规则，可以改善A-V模型在不同材料不同加载方式下棘轮效应的预测结果.陈小辉等[14]分析了Z2CND18.12N不锈钢内压管道在位移控制下的棘轮应变.

本文通过改进参数γ2和引入Ramberg-Osgood(R-O)模型及各向同性硬化，使改进A-V模型能更精确地预测材料的棘轮效应.

1 本构模型

Armstrong和Frederick[1]将非线性随动硬化A-F模型表示为

dα=Cdεp-γ1αdp.

(1)

式中：α表示背应力张量；dα为背应力增量张量；dεp为塑性应变增量张量；C和γ1为材料参数，是由单轴应力-应变滞环曲线的形状和大小确定；dp为累积塑性应变增量，

(2)

Cdεp包含了应变硬化效应；γ1αdp为动态恢复项，用于描述背应力的非线性特性.

A-F模型预测的材料棘轮效应低于试验值，Bower[10]通过加上了一个与背应力相关的附加项及其演化方程，对A-F模型中的动态恢复项进行了修正，即

dα=Cdεp-γ1αdp,

(3)

db=γ2(α-b)dp.

(4)

Bower模型包含3个独立的材料参数C，γ1和γ2.参数C和γ1控制着应力-应变滞环曲线的形状和大小，而式(4)中参数γ2控制棘轮应变率，b为附加的运动变量，初值为零.

Ahmadzadeh和Varvani-Farahani[11]为了提高Bower本构模型的棘轮效应预测能力，引入了系数δ，对Bower模型进行了修正，即A-V模型：

dα=Cdεp-γ1(α-δb)dp,

(5)

db=γ2(α-b)dp.

(6)

A-V模型由4个材料常数C，γ1，γ2和δ组成.材料常数C和第一反馈速率γ1控制着应力-应变滞后环的大小；参数γ2控制棘轮速率.由式(6)可以看出，在循环加载过程中，附加运动变量b随背应力α的运动具有“指数滞后”.参数γ2可以控制(α-b)的平均速率值.A-V模型对第一阶段预测棘轮应变值明显低于试验值，并且棘轮应变率随着循环次数的增加而快速趋于稳定，利用A-V模型模拟预测大循环棘轮效应时也不够准确.

2 A-V模型参数确定

A-V模型在循环加载条件下，参数的选取可以根据不同工况下材料的棘轮效应来确定[11].用Z2CND18.12N[15]材料在平均应力为100 MPa，应力幅值为250 MPa作用下的单轴棘轮效应试验数据来确定模型参数.

参数C和γ1的选取与材料和载荷大小直接相关，其控制滞环曲线的形状和大小[11].为了获得与试验数据一致的滞环曲线形状和尺寸，通过改进模型的闭式解来确定不同的参数C和γ1.

图1给出了Z2CND18.12N奥氏体不锈钢在平均应力σm=100 MPa和应力幅值σa=250 MPa下参数C=160 GPa和γ1=800 MPa对应的滞环曲线形状和大小.可看出，随着循环次数的增大，滞环曲线连续向前运动.图2为Z2CND18.12N奥氏体不锈钢在单轴应力循环下(σa=175 MPa,σm=150 MPa)的典型棘轮响应，以及不同参数γ2和δ对A-V模型的预测结果.参数γ2和δ改进了A-F模型过高预测的棘轮效应和Bower模型预测结果过早发生塑性安定.从图2a中可以看出，当γ2=0时，A-V模型退化为A-F模型，产生恒定的棘轮速率.γ2值越大，棘轮应变累积越容易趋于安定.γ2=350时，模拟与试验结果吻合较好.图2b揭示了δ值越大，棘轮应变累积越容易趋于安定.

图1 参数C=160 GPa和γ1=800 MPa对棘轮应变影响

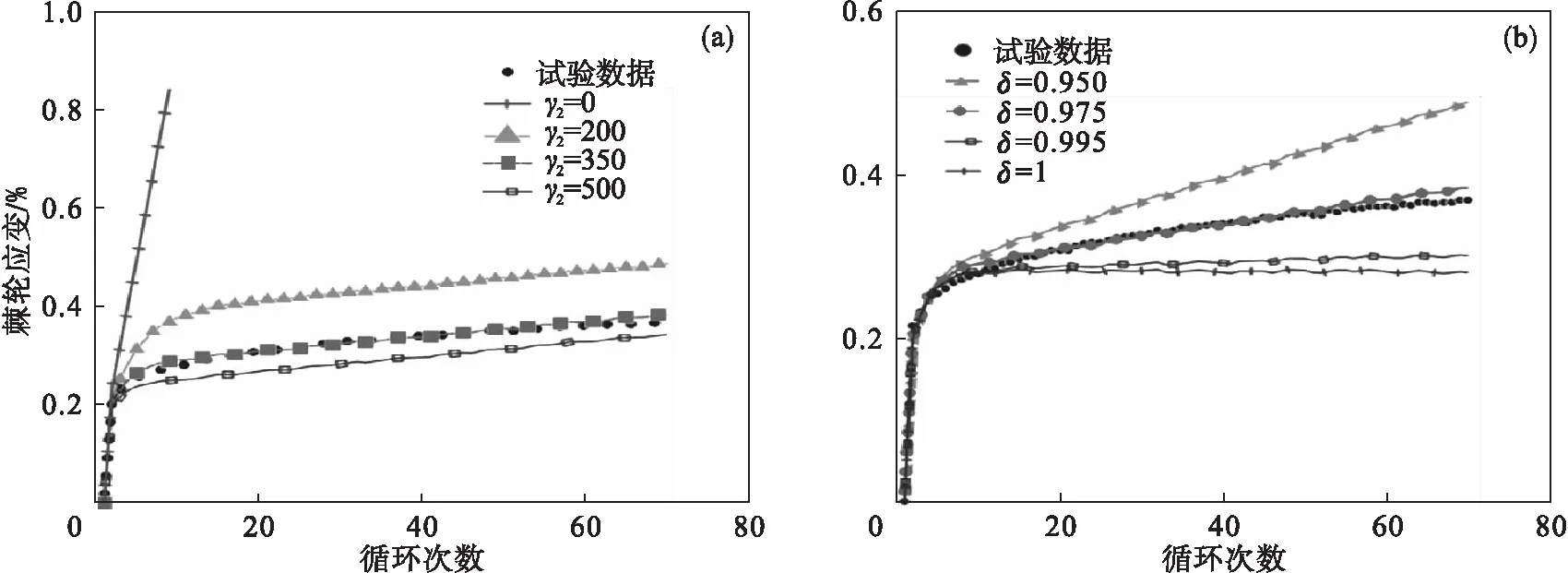
图2 应力循环中参数γ2和δ的变化对棘轮应变的影响

3 改进模型

R-O模型是固体力学中描述弹塑性应力-应变曲线的一个经典理论模型[16].在实际工程中，金属材料的循环应力-应变曲线可以采用R-O模型描述[17]，通过引入R-O模型来改善A-V模型预测棘轮应变时的缺陷，公式为

(7)

式中：ε为应变；σ为应力；E为材料初始弹性模量；K为应变硬化相关系数；n为应变硬化指数.

Z2CND18.12N不锈钢在室温下表现出明显的循环硬化特性[18]，公式为

(8)

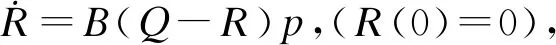
(9)

(10)

由文献[11]知，参数γ2控制棘轮应变速率，并校准各种材料和应力水平的棘轮响应.从A-V模型预测的材料单轴棘轮效应的结果可以发现，A-V模型对第一阶段预测棘轮应变值明显低于试验值，棘轮应变率随着循环次数的增加而逐渐稳定，模拟预测棘轮效应时不够准确.为了更准确地描述材料的棘轮应变演化规律，本文进一步分析了γ2的影响，从图3a中可以看出，γ2越大，棘轮应变稳定的速度越快.值得注意的是，不同γ2处的棘轮应变曲线与试验曲线有交集，且该交集随γ2的减小而逐渐延迟，这意味着在不同循环次数下使用不同γ2可以获得更好的结果.因此，根据文献[19]对参数γ2的改进方式，本文提出了参数γ2随累积塑性应变p的演化规律见图3b.

(11)

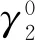
(12)

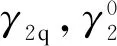
本文采用Z2CND18.12N[15]和SS316L[20]奥氏体不锈钢的单轴棘轮试验数据来验证A-V模型和改进模型的预测效果，其材料参数见表1.

图3 改进模型的参数γ2对棘轮应变的影响及其演化规律

表1 机械性能和材料相关棘轮参数

图4给出了平均应力σm为100 MPa、应力速率为100 MPa/s和应力幅值σa为250 MPa下Z2CND18.12N奥氏体不锈钢单轴棘轮应变.图中对A-V模型、改进模型与试验数据进行了比较，结果表明改进模型明显提高了预测精度.

图4 Z2CND18.12N奥氏体不锈钢单轴棘轮效应

4 棘轮效应预测

4.1 平均应力对单轴棘轮效应的影响

图5和图6分别给出了相同应力幅值而不同平均应力下预测的Z2CND18.12N不锈钢和SS316L钢棘轮应变与其试验数据的对比.结果表明，随着平均应力值的增加，棘轮应变值增加；改进模型改善了A-V模型预测单轴棘轮效应的效果.

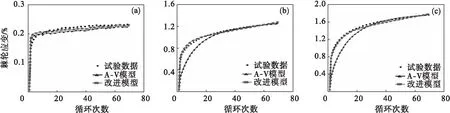
图5 当σa=175 MPa时Z2CND18.12N不锈钢循环次数对单轴棘轮应变的影响

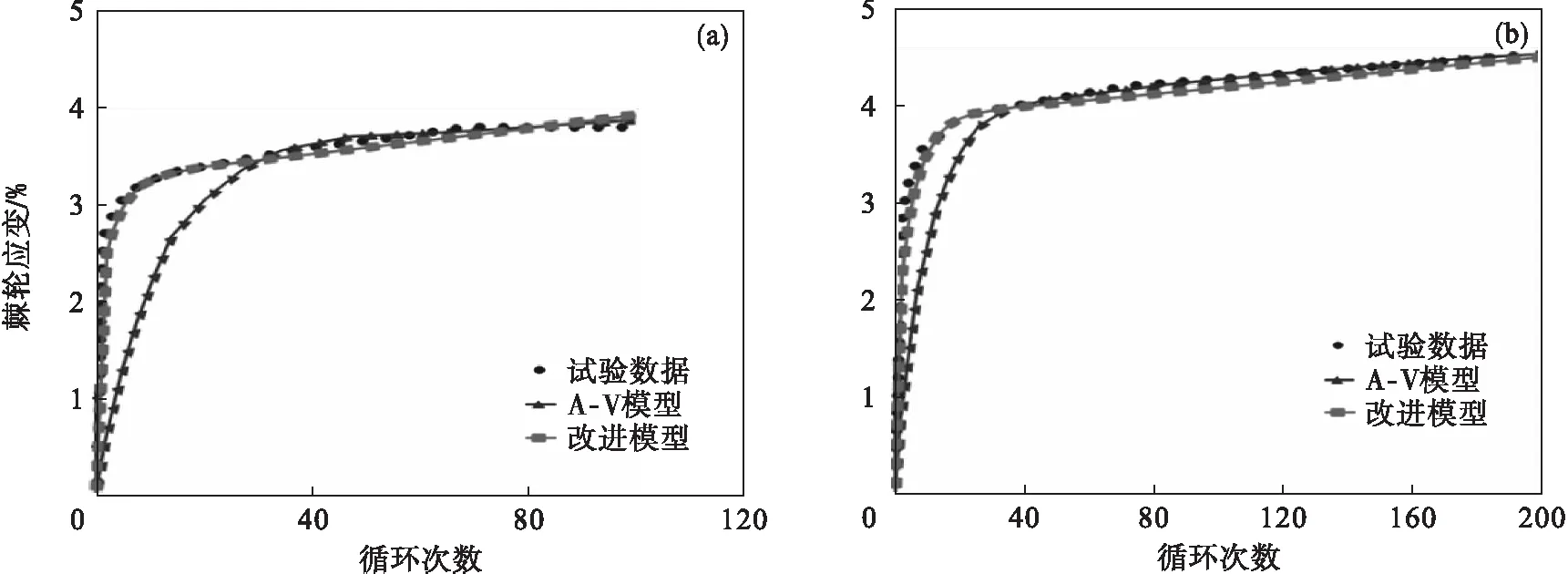
图6 当σa=247 MPa时SS316L钢循环次数对单轴棘轮应变的影响

4.2 应力幅值对单轴棘轮效应的影响

图7和图 8给出了相同平均应力不同应力幅值下预测的Z2CND18.12N不锈钢和SS316L钢棘轮应变与其试验数据的对比.结果揭示了，随着应力幅值的增加，棘轮应变值增加；改进模型改善了A-V模型预测单轴棘轮效应的效果.

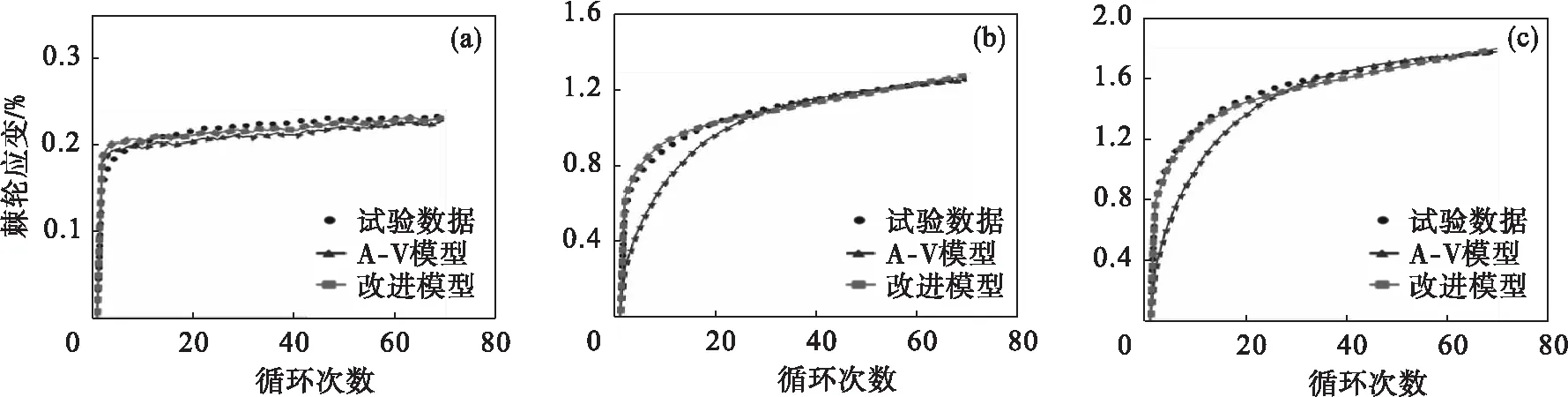
图7 当σm=175 MPa时Z2CND18.12N不锈钢循环次数对单轴棘轮应变的影响

4.3 应力比对单轴棘轮效应的影响

应力比可以综合反映加载应力幅值、平均应力和峰值应力对棘轮应变的影响[15].加载过程中最小应力σmin和峰值应力σmax的比值定义为应力比，即r=σmin/σmax.

4.3.1σmax=350 MPa恒定

1)r=0时，σmin=0 MPa；

2)r=-0.143时，σmin=-50 MPa；

3)r=-0.429时，σmin=-150 MPa.

图9给出了σmax=350 MPa时Z2CND18.12N不锈钢单轴棘轮应变曲线.从图中可以看出，改进模型改善了A-V模型预测效果.

随着循环次数的逐渐增加，棘轮应变率逐渐衰减，且棘轮应变随着应力比的改变而产生明显的变化.可见，峰值应力不变，应力比大小对棘轮应变的影响显著.

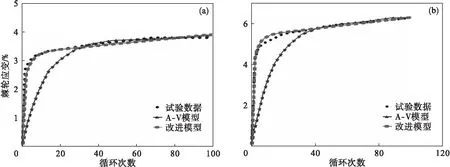
图8 当σm=52 MPa时SS316L钢循环次数对单轴棘轮应变的影响

4.3.2σmin=-25 MPa恒定

1)r=-0.077时，σmax=325 MPa；

2)r=-0.067时，σmax=375 MPa；

3)r=-0.059时，σmax=425 MPa.

图10给出了当σmin=-25 MPa时Z2CND18.12N不锈钢单轴棘轮应变曲线.从图中可以看出，随着循环次数的逐渐增加，棘轮应变率逐渐衰减，最终会达到饱和的棘轮安定状态.棘轮应变受应力比的影响显著.

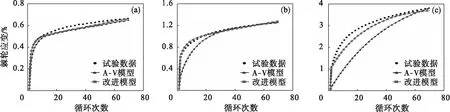
图9 当σmax=350 MPa时Z2CND18.12N不锈钢单轴棘轮应变

图10 当σmin=-25 MPa时Z2CND18.12N不锈钢单轴棘轮应变

4.4 加载历史对单轴棘轮效应的影响

由图11a可知，改进模型预测结果优于A-V模型预测结果.棘轮应变随着平均应力的增大而逐渐增大，而且增大了棘轮应变累积速率；由图11a还知，平均应力减小到150 MPa时，棘轮应变停止增加.这可以归因于之前的高平均应力加载，从而提高了材料的屈服极限.当材料恢复到低平均应力循环时，将不再屈服.这是一个完整的弹性应力循环.在这种加载条件下，可以认为已达到稳定状态.

由图11b可知，棘轮应变随着应力幅值的增大而逐渐增大，同时增大了棘轮应变累积速率.

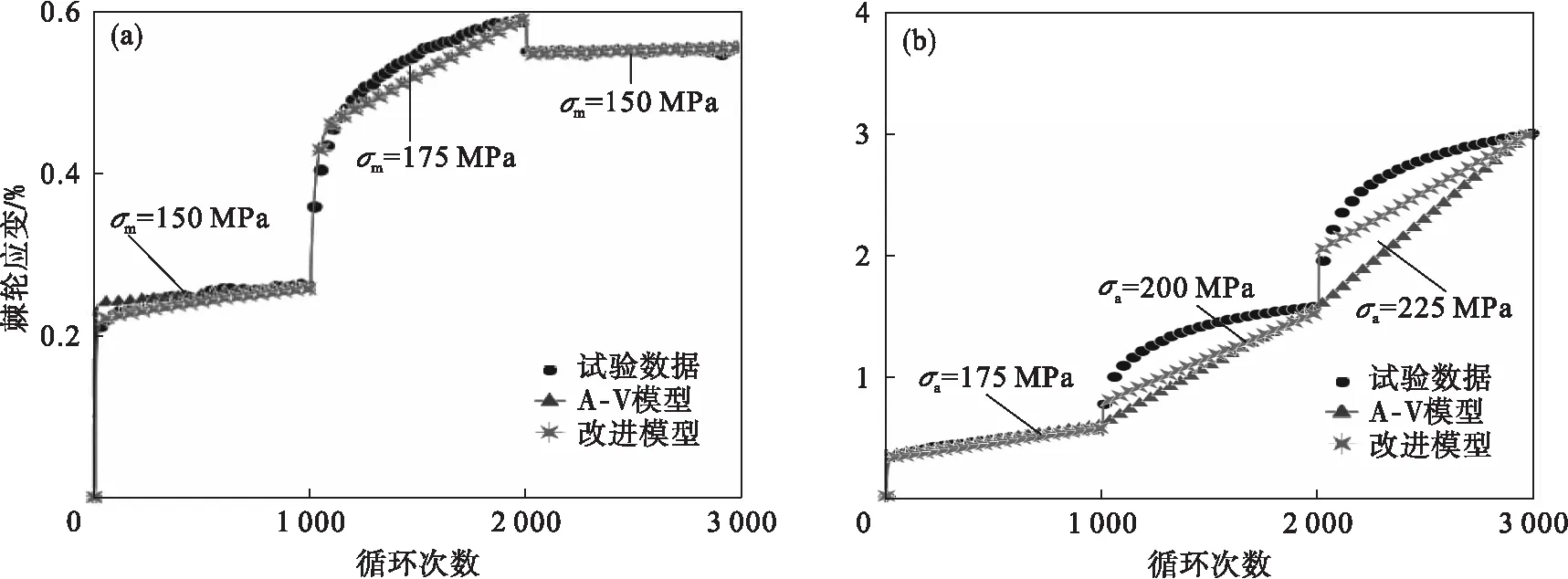
图11 多步加载下Z2CND18.12N不锈钢单轴棘轮应变

图12给出了两步低-高加载条件下的SS316L[20]预测棘轮应变和试验数据的对比.应力幅为247 MPa，第一步平均应力为52 MPa，第二步为78 MPa每一步循环100次.从图中看出，改进模型预测棘轮应变和试验数据在图中非常一致；在多步加载条件下，后续加载步会受到前一加载步的影响，加载顺序会对棘轮大小和应力循环趋势造成一定的影响.结果表明，改进模型改善了A-V模型预测结果.

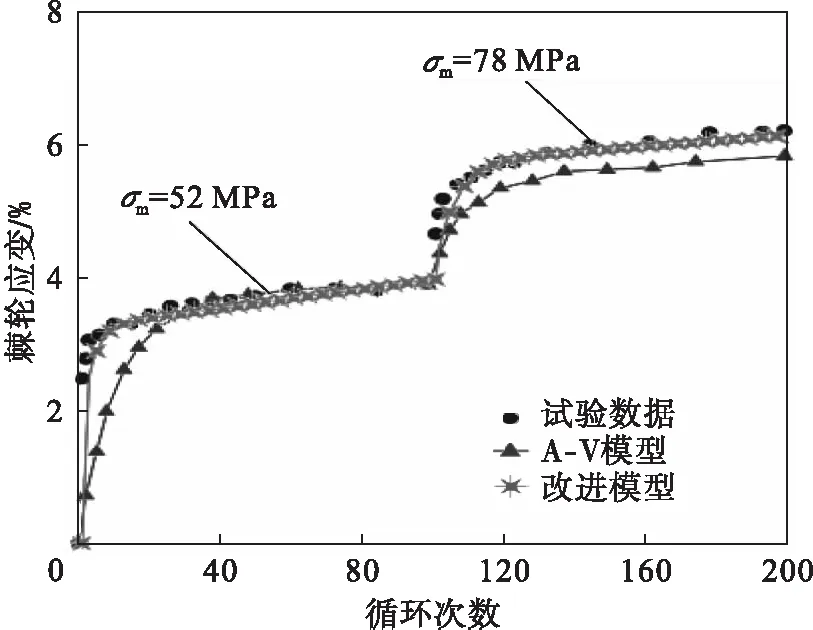
图12 σa=247 MPa时多步加载下SS316L钢单轴棘轮应变

5 结 论

1) 本文对A-V模型的参数γ2进行了改进，同时还将Ramberg-Osgood模型和各向同性硬化引入A-V模型，用以改善A-V模型对材料棘轮效应的预测.

2) 本文采用改进模型预测了Z2CND18.12N奥氏体不锈钢和SS316L钢的单轴棘轮效应，分析了平均应力、应力幅值、应力比和加载历史对单轴棘轮效应的影响.结果表明，改进的A-V模型对材料的棘轮应变预测结果比A-V模型效果好，且与试验数据较为一致.