半圆形凸起与沉积谷地相连地形对SH波的散射

吕晓棠，安静波

（合肥学院 建筑工程系，合肥 230022）

研究弹性波入射时局部场地条件下的地面运动规律，既是弹性波散射理论研究的重要课题，又对工程实践有广泛的指导意义。二十世纪中后期以来，局部场地条件对地震动影响问题的研究取得了大量有意义的成果。波函数展开和复变函数法有效地解决了凸起、凹陷地形对平面SH波的散射问题［1－7］。半空间中圆弧形沉积盆地对SH波的散射［8］，楔形空间中圆弧形沉积对平面SH波的散射解析解［9］，都假定沉积谷地中为单一介质。在圆弧形层状沉积河谷场地对平面SH波入射下动力响应分析［10］中，讨论了沉积谷地土层排列顺序对动力响应的放大作用。齐辉等［11－12］讨论了直角域中SH波的散射问题。已有成果大都是针对某一种地形对弹性波的散射问题进行研究，对于由两种或两种以上地形共同组成的复杂场地对弹性波散射问题的讨论并不多见。

在自然界中，广泛存在凸起与沉积谷地相连等复杂地形。研究这些地形对SH波的散射问题，不仅具有一定的理论意义，而且有广阔的工程应用前景。

本文利用复变函数和移动坐标法研究了半圆形凸起与半圆形沉积谷地相连地形对SH波的散射问题。求解时，将整个求解区域分为三部分。首先，在三个部分中分别构造满足各自边界条件的位移解，然后利用复变函数法和移动坐标法使之满足“公共”边界和半圆形沉积层的边界条件，从而建立起求解该问题的无穷代数方程组。

1 问题的表述

半圆形凸起与半圆形沉积层相连地形的模型如图1所示，半空间水平地表边界记为S，半圆形凸起地形边界记为C，半径为a，圆心为O1；半圆形沉积层地形凹陷边界记为，水平边界记为，半径为R，圆心为 O2；

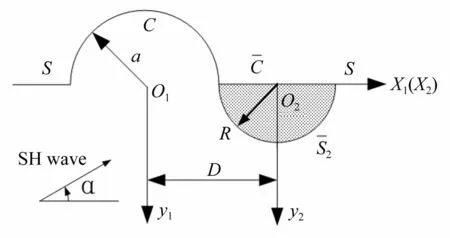
图1 半圆形凸起与半圆形沉积层相连地形模型Fig．1 Model of a semi-cylindrical hill adjoins a semi-cylindrical alluvial valley

求解该模型对稳态平面SH波的散射问题，就是要满足水平边界S，凸起边界C上应力自由，并且在半圆形沉积层凹陷边界上满足应力、位移连续的边界条件下，求解SH波的控制方程。采用“分区”的方法，将整个求解区域分割成3部分，如图2所示。区域Ⅰ为包括边界C和在内的圆形区域；半圆形沉积层为区域Ⅲ，包括沉积层水平边界和凹陷边界；余下部分为区域Ⅱ，包括边界S和。其中，和为区域Ⅰ、Ⅱ的公共边界和为区域Ⅱ、Ⅲ的公共边界，在两个公共边界上应该分别满足应力、位移连续的边界条件。

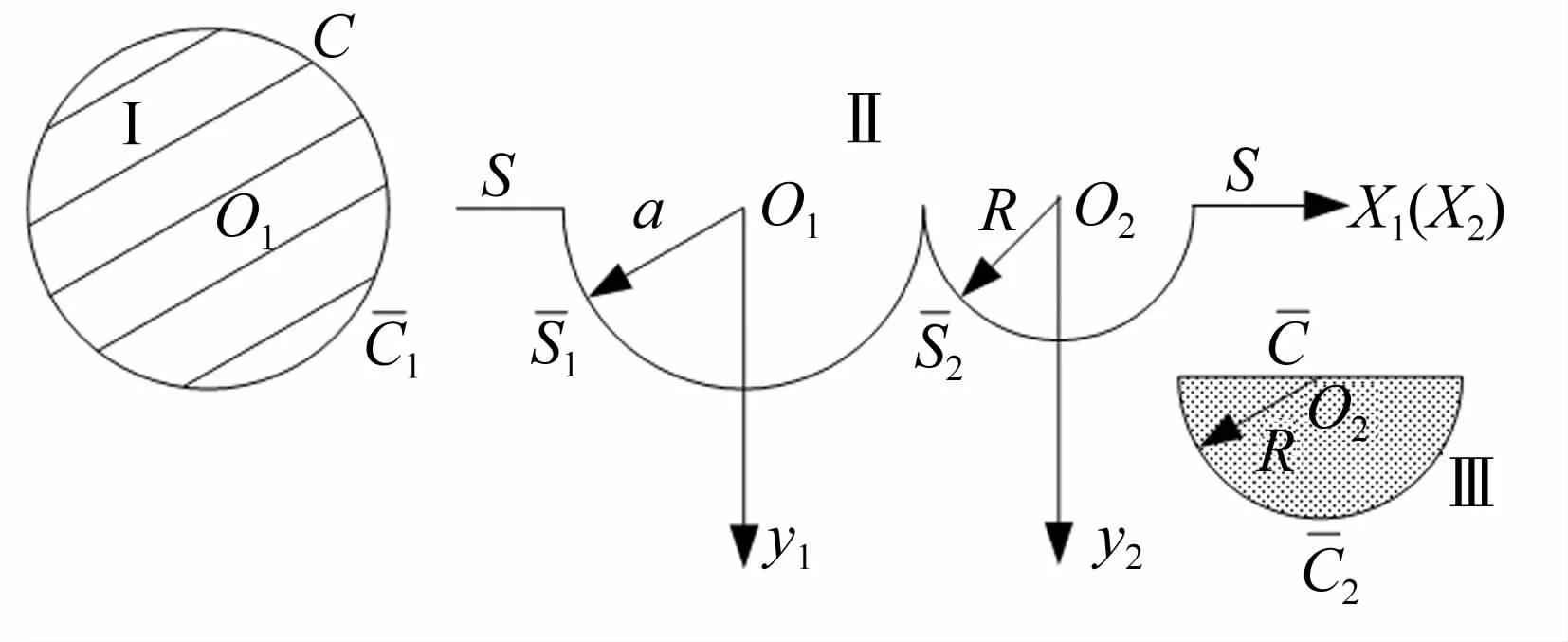
图2 求解区域的分割Fig．2 The division of the solution domain

2 问题的求解

2．1 控制方程

在各向同性、均匀、连续的介质中研究弹性波对夹塞的散射问题，其最为简单的模型就是反平面剪切运动的SH波模型。引入复变量z＝x＋iy＝x－iy，在复平面（上，对于稳态情况，位移 W（x，y，t）要满足运动方程

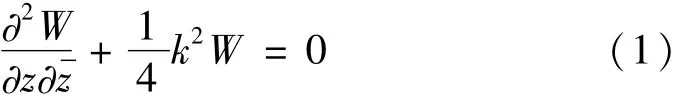
其中：W为位移函数，位移函数与时间的依赖关系为e－iωt（以下略去谐和因子 e－iωt）。k＝ω／cs，ω为位移 W（x，y，t）的圆频率介质的剪切波速，ρ、μ分别为介质的质量密度和剪切模量。

在极坐标系下，相应的应力可表达为

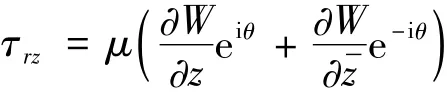
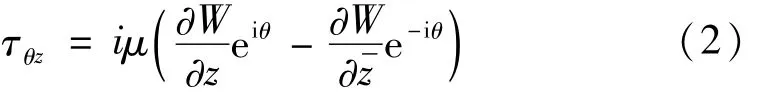
2．2 相关问题

2．2．1 区域Ⅰ内的驻波

如图2所示，以半圆形凸起的圆心O1为原点，建立 X1－O1－Y1坐标系，对应复平面（z1）；以半圆形凹陷的圆心O2为原点建立X2－O2－Y2坐标系，对应复平面（z2）。D为圆心O1、O2之间的距离。

在圆域Ⅰ内求解一个驻波解，要求其满足上边界C上应力自由，下边界上应力任意的边界条件，由文献［6］可知，在复平面（z1）中，这样的驻波解可写为

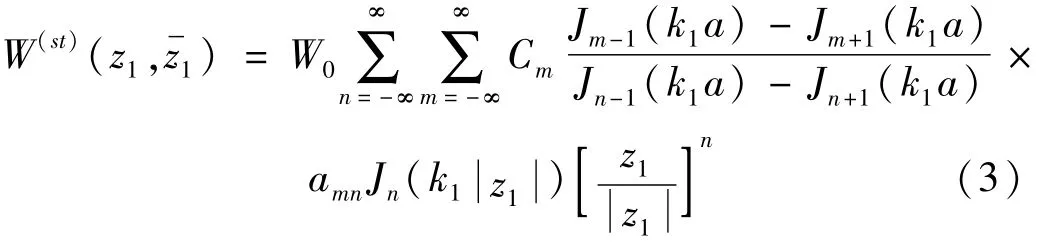
相应的应力为

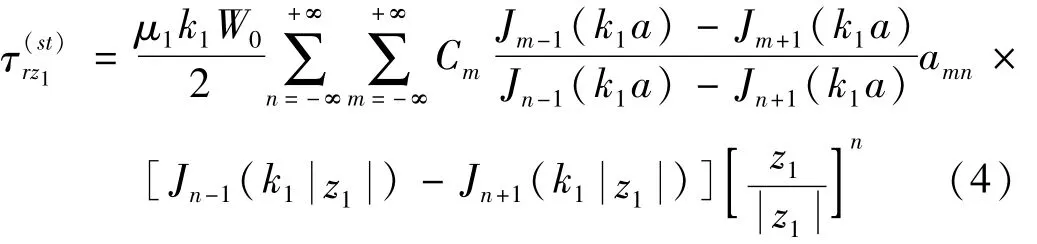
其中：

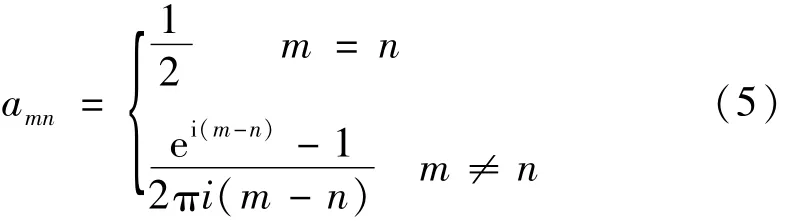
ki＝ω／csi，csi为剪切波速。本文中，当i＝1时代表沉积层外介质的各种参数，i＝2时代表半圆形沉积层的各种参数，例如ρ1，μ1代表沉积层外介质的质量密度和剪切模量；ρ2，μ2代表沉积层的质量密度和剪切模量。

2．2．2 区域Ⅱ内的波函数

在入射SH波的作用下，区域Ⅱ中存在散射波场W，由以下几部分组成：由半空间水平界面产生的反射波 W（r）；由半圆形凹陷边界产生的散射波，；并且区域Ⅱ中的总波场 W应该满足半空间表面S上应力自由的边界条件。

在复平面（z1，）中，满足S上应力自由的散射波W，W可表示为

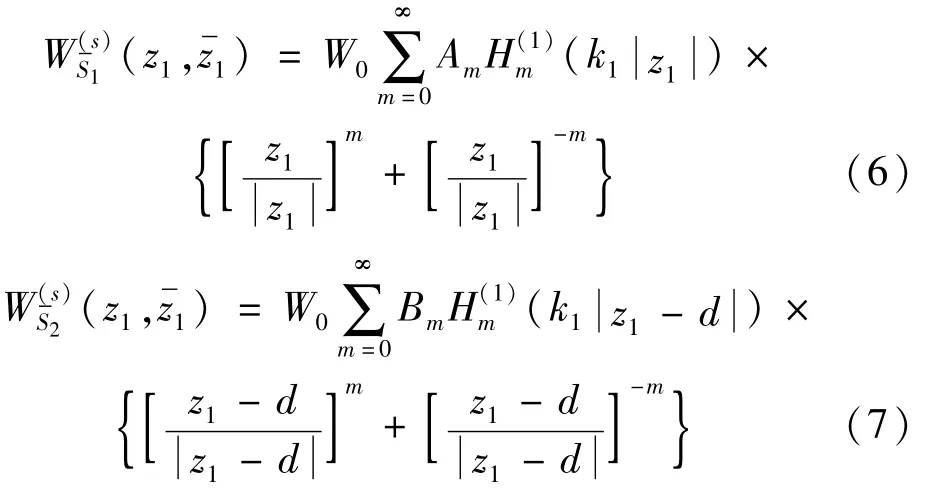
其中：d是在复平面（z1，z1）中，半圆形沉积层圆心的复坐标。

相应的应力为

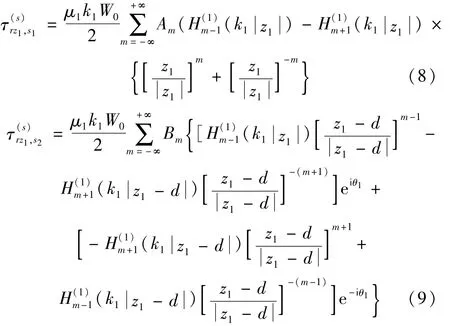
由SH波散射的多极坐标法知，在复平面（z2，）

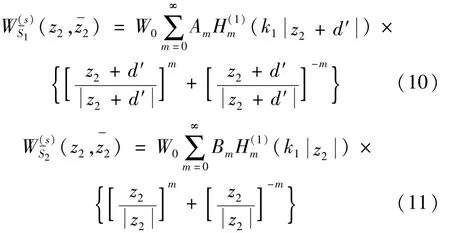
其中：d′是在复平面（z2，）中半圆形凸起圆心的复坐标。

相应的应力可依照此方法由式（8）、（9）得到。

2．2．3 区域Ⅲ中的驻波

SH波入射时，半圆形沉积层中产生驻波，这个驻波应该满足沉积层水平边界上应力自由的边界条件。在复平面（z2，2）下，区域Ⅲ中这样的驻波可表示为

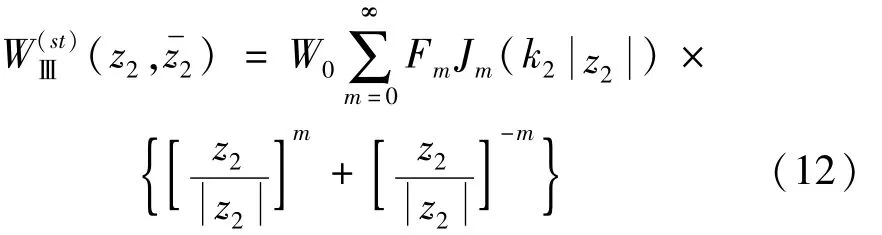
相应的应力表达式为

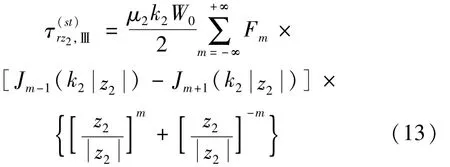
2．2．4 入射波和散射波

在复平面（z1，）上，入射波和反射波可写为

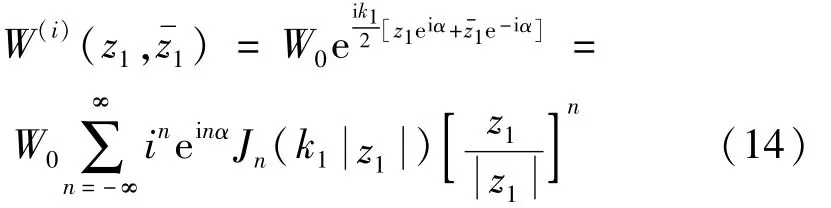
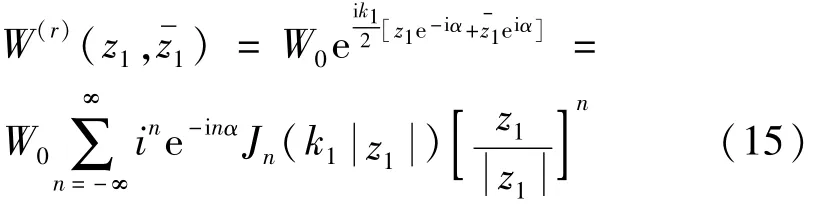
相应的应力可表示为

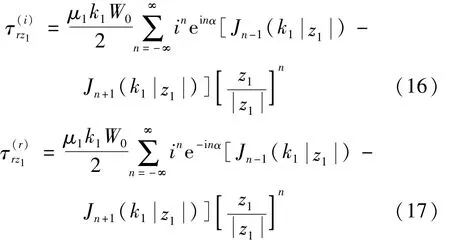
复平面（z2z2）上，入射波和反射波可写为

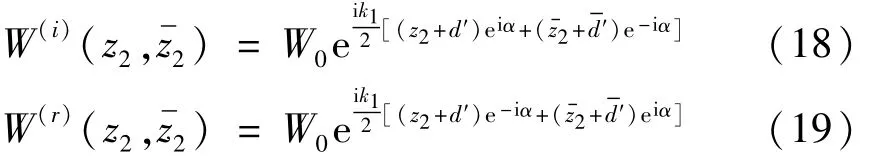
相应的应力可表示为

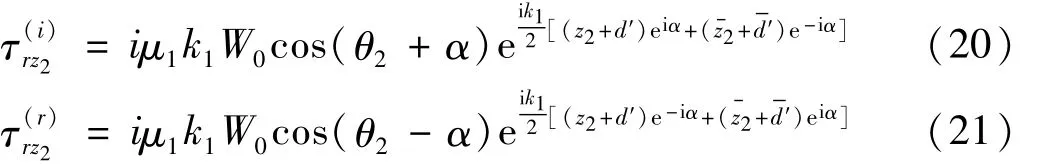
2．3 边界条件及定解方程组

在两个公共边界上分别满足应力、位移连续的边界条件，可得到求解本问题的定解方程组

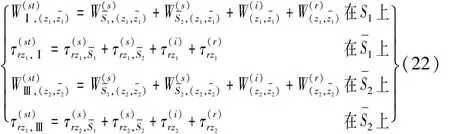
将位移和应力的表达式代入式（22），在方程两边同时乘以 e－inθ，并在区间（－π，π）上积分，可得到决定未知系数Am，Bm，Cm，Fm的无穷代数方程组。

2．4 地面位移幅值

研究半圆形凸起与半圆形沉积层相连地形对SH波的散射问题，就要求给出水平面上任一观察点上地震动变化与SH波的波数η和入射角α的关系。由于入射SH波的作用，圆域Ⅰ内的波场为W，区域Ⅲ中的波场为W，而弹性半空间区域Ⅱ中的总波场则可以写成

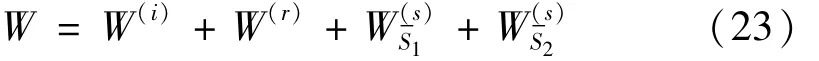
入射波波数为

或者

其中：λ为入射波的波长，或写为η＝2a／λ。

3 算例和结果分析

作为算例，图3给出3组无量纲参数比：μ1／μ2＝2／1，即半圆形沉积层相对于半圆形凸起比较“软”；μ1／μ2＝1／1，即半圆形沉积层与半圆形凸起具有相同的剪切模量和密度，此时可认为半圆形沉积层不存在，计算模型应退化为半空间中单独的半圆形凸起地形；μ1／μ2＝1／2，即半圆形沉积层相对于半圆形凸起比较“硬”。

如图3中，x／a＝－1点代表半圆形凸起地形与水平面相交处的几何位置，x／a＝1点代表凸起与沉积层相交的位置；x／a＜1代表凸起地形表面上各点。1＜x／a＜3代表沉积层表面上各点，x／a＝3点代表沉积层与水平面相交处的几何位置，x／a＜－1代表水平表面上诸点的位置。

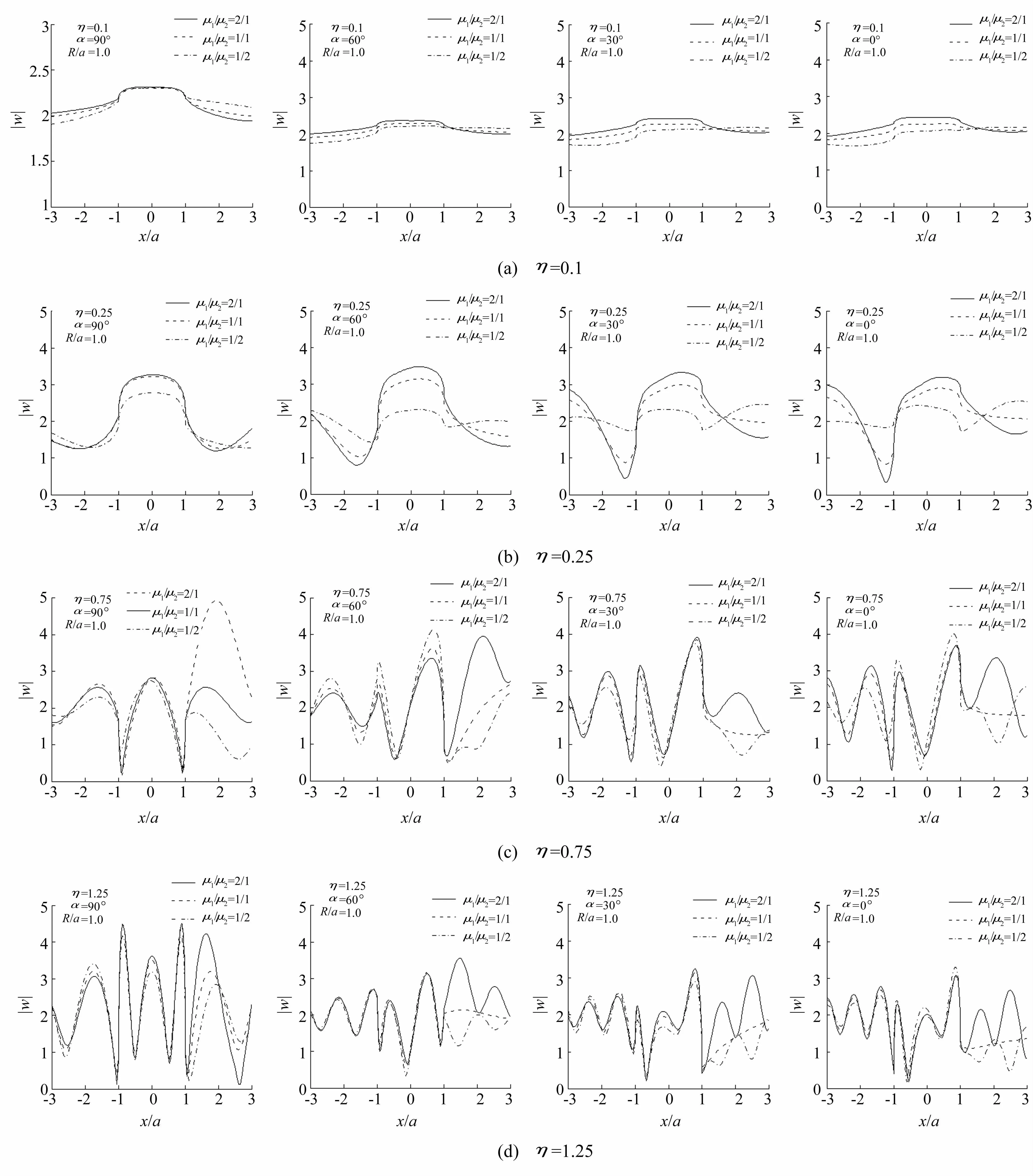
图3 地表位移幅值随x／a的变化Fig．3 Variation of surface displacement amplitudes with x／a

图3给出SH波以不同波数η，不同入射角α入射时，以上3种情况下半圆形凸起与沉积层相连地形地表位移幅值的变化情况。

（1）当 μ1／μ2＝1／1时，地表位移的变化规律与半空间中单独凸起地形位移的变化规律［3］一致，可以认为消除了沉积层的影响。

（2）由图 3（a）、（b）可见，当 η＝0．1和 η＝0．25时，除α＝90°的情况外，凸起部分位移幅值W均随μ1／μ2的减小而降低，也就是说，当 μ1／μ2＝2／1即沉积层较“软”时，对凸起部分W起到放大作用，使其大于单独半圆形凸起即 μ1／μ2＝1／1的情况；而 μ1／μ2＝1／2即沉积层较“硬”时，可明显降低凸起部分的位移。例如，当 η＝0．25，α＝60°时，μ1／μ2＝2／1相对于 μ1／μ2＝1／1的情况，凸起顶点位移幅值提高了10%；而μ1／μ2＝1／2相对于 μ1／μ2＝1／1的情况，凸起顶点位移幅值降低了25%。

（3）高频 η＝0．75，1．25入射时，由图 3（c）、（d）可见，沉积层对凸起部分位移有不同程度的影响，但影响程度比低频情况小。同时，相对于单独凸起的情况，凸起右侧沉积层表面位移显示出明显的振荡趋势，而且沉积层越“软”，表面位移越大。

（4）半圆形凸起右侧沉积层的存在，对凸起左侧半空间水平表面的位移也有显著影响。η＝0．1时，沉积层越“软”，对凸起左侧水平表面位移的放大作用越明显。随着η值的增大，这种影响表现为不同程度的放大和缩小作用。

图4给出SH波垂直入射，R／a＝1．0和 R／a＝0．5时，半圆形凸起顶点位移幅值随波数变化的反应谱。由图可见，当 μ1／μ2＝1／1时，凸起顶点位移幅值反应谱，其变化规律与文献［3］一致。当R／a＝1．0时，在η＝0．1～1．25的频段内，凸起顶点位移幅值随 μ1／μ2值的减小而降低，说明半圆形沉积层较“硬”时，在此频段内对凸起顶点位移有一定的减震作用。当R／a＝0．5时，这种减震作用仍然存在，但频段变为η＝0．1～1．1。

图4 凸起顶点位移幅值反应谱Fig．4 Response spectrum of the hill peak displacement amplitudes

4 结 论

本文采用复变函数法研究了SH波入射下半圆形凸起与沉积谷地相连地形的地震动情况。给出了在半圆形沉积层的影响下，凸起地形对SH波散射的位移场和应力场，通过具体算例，讨论了入射波波数ka，入射角α，沉积层半径与凸起半径之比R／a以及周围介质与沉积层的各种材料参数比等对凸起部分地表位移幅值的影响。具体算例表明：

（1）当SH波低频斜入射时，较软的沉积层对凸起部分表面位移放大作用明显；而高频情况下影响相对较小。

（2）当入射波频率η＝0．1时，沉积层的存在对凸起左侧水平表面位移的影响不能忽略。

（3）SH波垂直入射时，沉积谷地的半径越大（相对于凸起），对凸起顶点位移的放大或缩小效应也体现在较长的入射频段内。

［1］Trifunac M D．Scattering of plane SH-waves by a semi-cylindrical canyon［J］． Earthquake Engineering and Structural Dynamics，1973（1）：267－281．

［2］Liu Dian-kui，Han Feng．Scattering of plane SH-waves by a cylindrical canyon of arbitrary shape［J］．Int．J．Soil．Dynamic and Earthquake Engineering，1991，10（5）：249－255．

［3］Yuan Xiao-ming，Men Fu-lu．Scattering of plane SH-waves by a semi-cylindrical hill［J］． Earthq． Eng． and Struct．Dynamics，1992（21）：1091－1098．

［4］崔志刚，邹永超，刘殿魁．SH波对圆弧形凸起地形的散射［J］．地震工程与工程振动，1998，18（4）：8－14．CUI Zhi-gang，ZOU Yong-chao，LIU Dian-kui．Scattering of plane SH-wave by a cylindrical hill of circular-arc cross section［J］． Earthquake Engineering and Engineering Vibration，1998，18（4）：8－14．

［5］许贻燕，韩峰．平面SH波在相邻多个半圆形凹陷地形上的散射［J］．地震工程与工程振动，1992，12（2）：12－18．XU Yi-yan，HAN Feng．Scattering of SH-waves by multiple semi-cylindrical canyons［J］．Earthquake Engineering and Engineering Vibration，1992，12（2）：12－18．

［6］刘殿魁，王国庆．浅埋圆形孔洞附近的半圆形凸起对SH波的散射［J］．力学学报，2006，38（2）：109－128．LIU Dian-kui，WANGGuo-qing．Antiplane SH-deformation of a semi-cylindrical hill above a subsurface cavity［J］．Chinese Journal of Theoretical and Applied Mechanics，2006，38（2）：109－128．

［7］Liang Jian-wen，Luo H，Lee V W．Diffraction of plane SH waves by a semi-circular cavity in half-space［J］，Earthquake Science，2010，23（1）：5－12．

［8］袁晓铭 廖振鹏．圆弧型沉积盆地对平面SH波的散射［J］．华南地震，1995，15（2）：1－8．YUAN Xiao-ming，LIAO Zhen-peng．Scattering of plane SH waves by a cylindrical alluvial valley of circular-arc cross section［J］．South China Journal of Seismology，1995，15（2）：1－8．

［9］刘中宪，梁建文．楔形空间中圆弧形沉积对平面SH波的散射解析解［J］．天津大学学报，2010，43（7）：573－582．LIU Zhong-xian， LIANG Jian-wen． Analytic solution for diffraction of plane SH-waves by a circular alluvial valley in wedge-shaped space［J］． Journal of Tianjin University，2010，43（7）：573－582．

［10］梁建文，张郁山，顾晓鲁，等．圆弧形层状沉积河谷场地在平面SH波入射下动力响应分析［J］．岩土工程学报，2000，22（4）：396－401．LIANG Jian-wen，ZHANG Yu-shan，GU Xiao-lu，et al．Surface motion of circular-arc layered alluvial valleys for incident plane SH waves［J］．Chinese Journal of Geotechnical Engineering，2000，22（4）：396－401．

［11］齐辉，杨杰，李宏亮，等．含任意直线型裂纹的直角域中圆柱夹杂对 SH波的散射［J］．振动与冲击，2011，30（5）：208－212．QI Hui，YANG Jie，LI Hong-liang，et al．Scattering of SH-wave by a cylindrical Inclusion in right-angle plane with arbitrary beeline crack［J］．Journal of Vibration and Shock，2011，30（5）：208－212．

［12］齐辉，郭晶，杨杰．直角域非等腰三角形凸起对SH波的散射与地震动［J］．振动与冲击，2012，31（18）：157－162．QI Hui，GUO Jing，YANG Jie．Scattering of SH-wave and ground motion induced by scalene triangular hill on a right-angle field［J］．Journal of Vibration and Shock，2012，31（18）：157－162．