变载工况下钻机动力头传动系统动态特性
2014-09-20王清峰朱才朝史春宝
王清峰,朱才朝,史春宝,龙 威
(1.重庆大学 机械传动国家重点实验室,重庆 400044;2.中煤科工集团 重庆研究院,重庆 400039)
近年来,我国瓦斯抽放孔施工钻进技术得到了长足发展,产品规格和品种增多,性能也有了进一步的完善。中煤科工集团重庆研究院自主研发的全液压坑道钻机在各大煤矿的使用都获得了矿方的支持与肯定。但随着煤矿机械的不断发展,加上同行之间的竞争日趋激烈,市场对液压钻机的设计和制造要求日益提高,不仅要求承载的负荷越来越大,同时要满足体积小、结构合理、噪声和振动小、井下运输方便,适应不同地质情况下钻孔施工要求。动力头作为钻机的最终执行机构,其强度和可靠性直接影响着钻机的整机使用寿命,是钻机最为关键的部件之一。然而由于煤矿井下条件的复杂多变和地质条件的不可预知性,使得动力头的工况变得十分复杂,动力头就容易产生振动和噪声。
Kahraman等[1-2]建立了齿轮传动系统纯扭转振动模型;Lin等[3]建立了行星齿轮传动系统的扭转-横向振动模型,模型中将滚动轴承模拟为线性弹簧并考虑了齿轮的时变啮合刚度;孙涛等[4-5]建立了2K-H行星轮系弯-扭耦合非线性动力学模型,采用解析谐波平衡法求得了行星齿轮传动系统的非线性频响特性。
郑竹林针对ZYW-1200钻机动力头设计要求,提出了其设计和制造方案,并通过建立其三维有限元模型,对齿轮和轴进行了强度分析;李广田等对动力头齿轮进行参数化建模,并在ADAMS中创建了虚拟样机,分析了动力头的扭矩特性,并进行了仿真分析,仿真数据论证了阻尼系数与齿轮啮合力动载荷幅值大小的关系;黄宇辉等建立某钻机动力头齿轮三维模型,分析钻机工作时齿轮的受力情况,利用Workbench软件对齿轮弯曲应力进行有限元分析,为钻机回转器的设计与优化提供依据。
综上所述,因为煤矿用全液压坑道钻机动力头工况的复杂多变,振动和噪声表现得非常强烈,所以应对其传动系统进行动力学分析。
1 动力头传动系统动力学模型
以 ZYWL-6000全液压坑道钻机动力头为研究对象,如图1所示。液压马达提供输入转矩Tin,通过斜齿轮副g1-g2和齿轮副 g3-g4,传递给输出轴,而输出轴与卡盘固连在一起,卡盘将转矩 Tout传递给钻杆,从而带动钻头切削煤层或岩石。
考虑了齿轮副的时变啮合刚度、阻尼和传动误差,轴的扭转刚度和阻尼,轴承支撑刚度和阻尼,利用集中参数法建立齿轮传动系统的耦合动力学模型,如图2所示。各个构件以输入转矩作用下的各构件的转动方向为角位移的正方向,以齿面受压为正,径向和轴向位移则以各自坐标系的正方向为正。

图1 ZYWL-6000动力头传动形式示意图Fig.1 Sketch of the gear drive system of the ZYWL-6000

图2 动力头传动系统动力学模型Fig.2 Dynamic model of the gear drive system of the ZYWL-6000
图中:
kpz、cpz为轴承轴向支撑刚度和阻尼,p=1~4;
kpy、cpy为轴承径向支撑刚度和阻尼;
k23、c23为齿轮 g2和 g3所在轴的轴扭转刚度和阻尼;
kij、cij为齿轮副啮合刚度刚度和阻尼,(i,j)=(1,2;3,4);
eij为齿轮副综合啮合误差。
各个齿轮构件的坐标系和转动方向如图2所示。设齿轮副啮合线方向为y方向,其相互作用的动力学模型如图3所示。
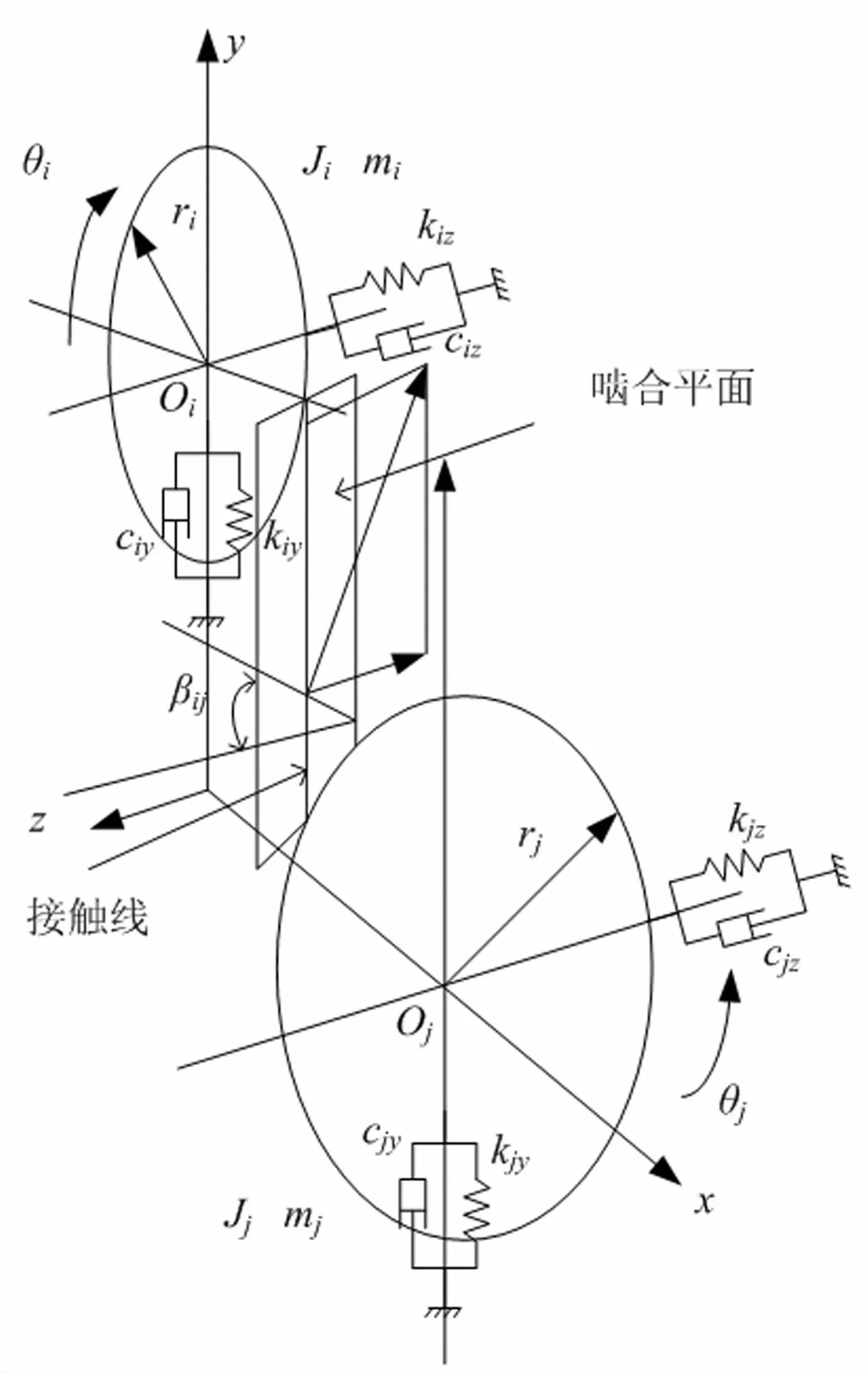
图3 斜齿轮副动力学模型Fig.3 Elastic deformation of shaft helical gear system
图中:
Ji、Jj、mi、mj为各个齿轮构件转动 惯 量和平移质量;
θi、θj为各个齿轮构件扭转角位移;ri、rj为各个齿轮构件基圆半径;βij为各个齿轮构件螺旋角。
由图3可以得到各个齿轮副沿啮合线方向上的弹性变形如式(1)和式(2)所示:

式中:
eijy为齿轮 y向综合啮合误差,eijy=eij·cosβ;
eijz为齿轮 z向综合啮合误差,eijz=eij·sinβ;
yi、yj、zi、zj为齿轮 y、z方向平移位移。
在建立动力头传动系统动力学耦合模型并得到其啮合线上弹性变形之后,便可推得其切向和轴向的动态啮合力如式(3)和式(4)所示。
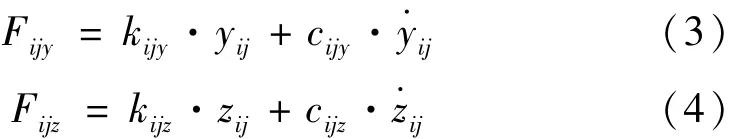
式中:kijy=kij·cosβ;cijy=cij·cosβ;kijz=kij·sinβ;cijz=cij·sinβ。
根据达朗贝尔原理推得动力头斜齿轮传动系统弯-扭-轴耦合动力学模型的振动微分方程如式(5)所示。
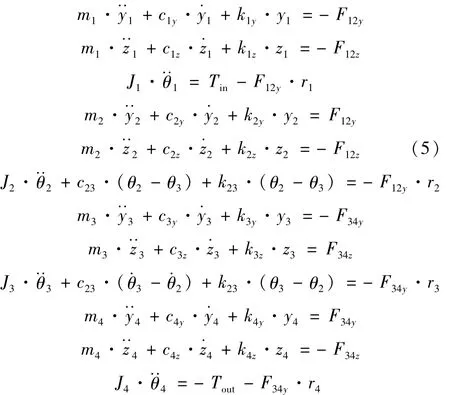
可将上面的方程化简后,写成如下矩阵形式如式(6)所示。

根据材料力学的方法可以分别得到传动轴扭转刚度和阻尼、轴承刚度和阻尼以及齿轮副时变啮合阻尼的计算公式[6-10],这里不再累述。
2 动力头传动系统激励分析
本文模型中考虑的齿轮内部激励包括刚度激励和误差激励。刚度激励表现为因啮合齿对数变化导致啮合综合刚度随时间周期变化从而引起齿轮轮齿啮合力周期变化。由齿轮加工、安装误差引起的齿廓表面相对于理想齿廓位置的偏移是齿轮系统的误差激励,这是啮合轮齿间的一种周期性位移激励。
2.1 内部激励
2.1.1 时变啮合刚度
先按GB 3480-1997计算出综合啮合刚度的峰值和平均值,然后按啮合频率将轮齿综合啮合刚度简化成矩形波周期函数,再将其展开成傅里叶级数并略去高阶项后整理得[10],如图4所示。
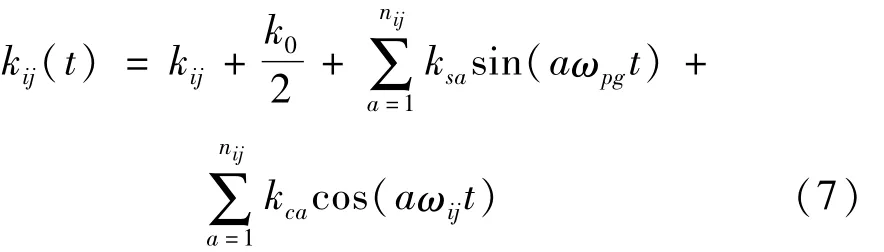
式中:ωij为啮合频率,nij为综合啮合刚度谐波阶次,kij为啮合刚度均值,ksa、kca为分别为各啮合副的第a阶正弦交变分量幅值和余弦交变分量幅值。
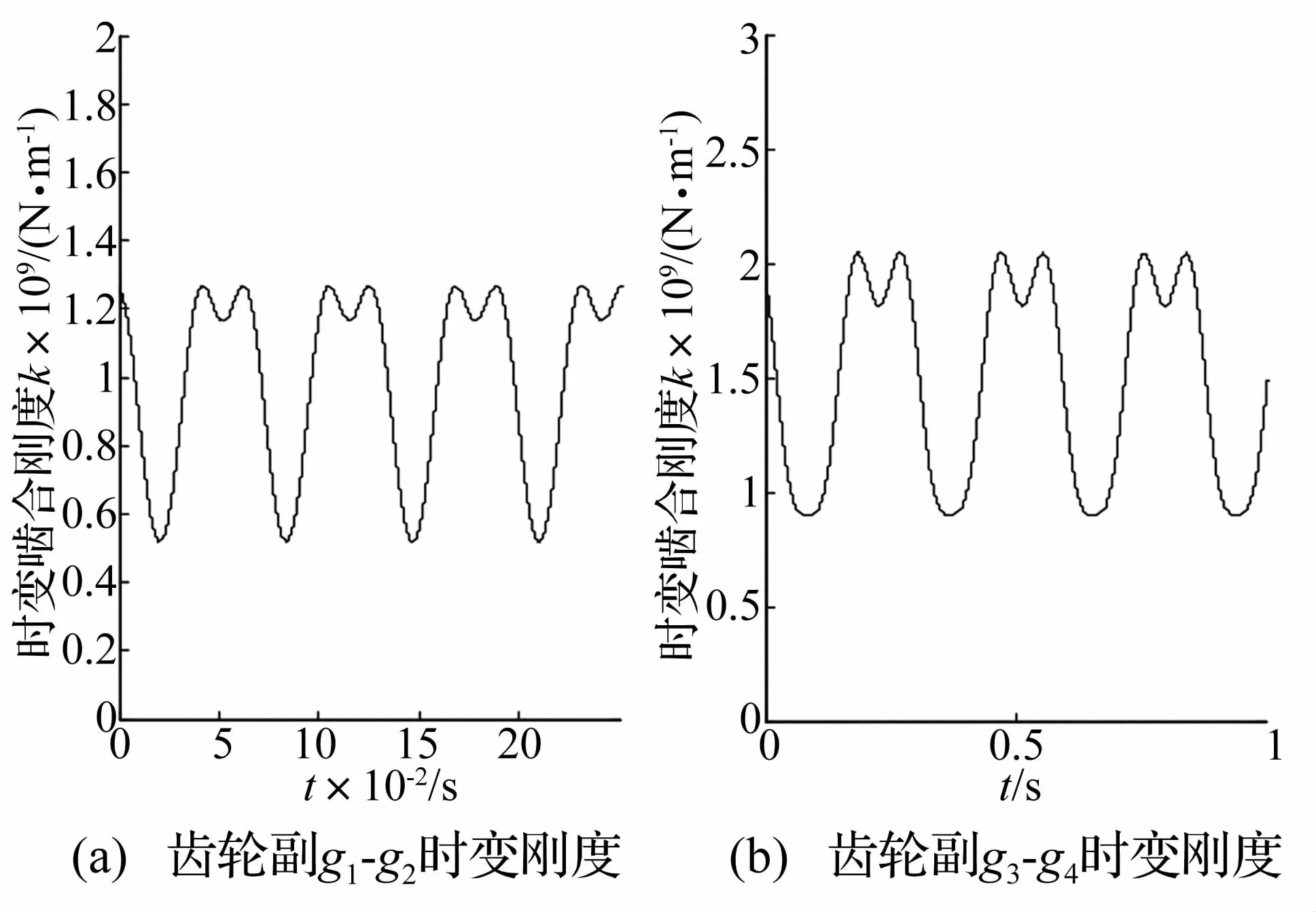
图4 齿轮时变啮合刚度示意图Fig.4 Curve of meshing stiffness
2.1.2 综合啮合误差
根据齿轮设计的精度等级确定齿轮的偏差,采用简谐函数进行误差模拟,则轮齿的齿形误差和基节误差可用正弦函数表示为[10],如图5所示。
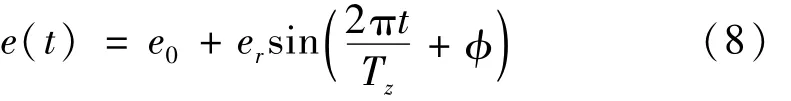
式中:e0、er分别为齿轮副综合啮合误差的常值和幅值,Tz为齿轮的啮合周期,Tz=60/(nzZ),nz、Z、φ分别为齿轮转速、齿数、相位角。
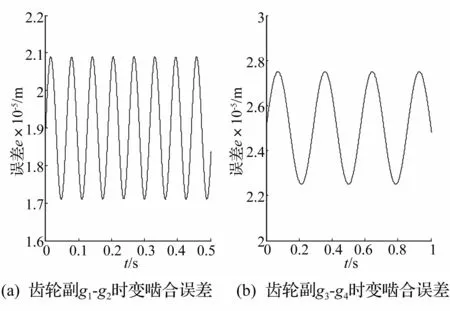
图5 综合啮合误差示意图Fig.5 Curve of meshing error
2.1.3 内部激励
将各级齿轮传动的啮合刚度曲线的变刚度部分和误差曲线在对应点处相乘,即得由齿轮刚度变化和误差引起的内部激励力如图6所示。
2.2 外部激励
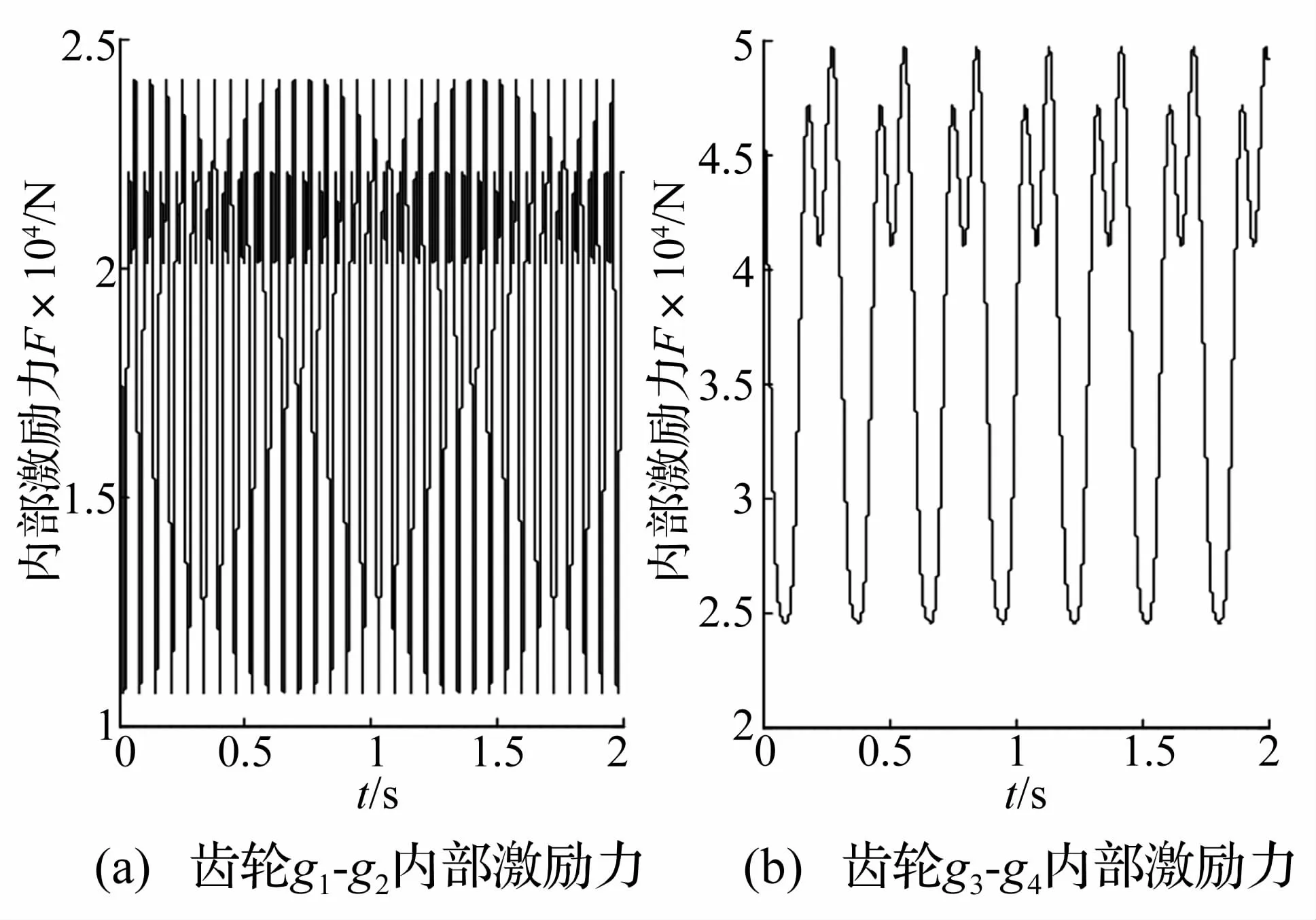
图6 内部激励力示意图Fig.6 Curve of meshing error Internal incentive force
钻机动力头在运动过程中所受的阻力矩主要来自钻具在钻进过程中所受的阻力矩,而钻具所受的阻力矩主要包括剪切力矩、摩擦阻力矩和分布阻力矩。剪切力矩是钻头切削刃切削岩石或则煤层产生的阻力,摩擦阻力矩即为钻刃与孔底摩擦所产生的的扭矩,分布阻力矩为钻杆外缘与孔壁间的岩粉摩擦形成。
ZYWL-6000全液压坑道钻机采用抗冲击性能较好、耐磨的胎体式PDC复合片钻头进行施工。假设通过PDC钻头刚体作用于单个PDC片的轴向载荷和水平载荷分别是F1和F2,在忽略一些次要因素后其受力示意图如图 7所示[12]。
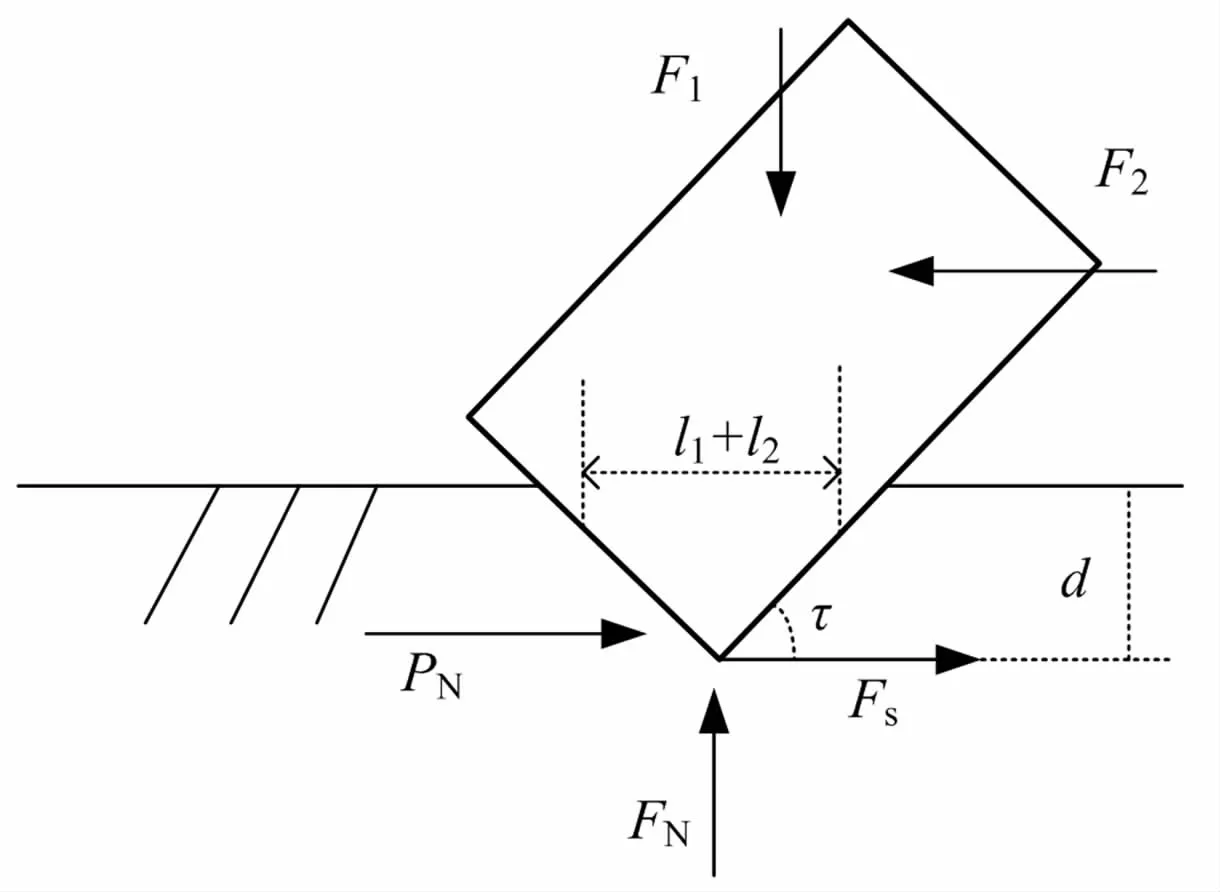
图7 单个PDC受力示意图Fig.7 Schematic diagram of force on a single PDC
图中:
FN为单个PDC片轴向压入一定深度d后,岩石对PDC的反作用力;
PN为单个PDC片水平切削一定极限位移达到破碎岩石要求时后,岩石对PDC的反作用力;
Fs为PDC的底部与岩石之间的水平摩擦力;
F1、F2为PDC片受到的轴向力和切向力;
τ为切入角,单片PDC与弹性体表面之间夹角;
d为压入深度,d=l1·cotτ=l2·tanτ。
通过对单个PDC片进行受力分析,可得到[12]:


式中:
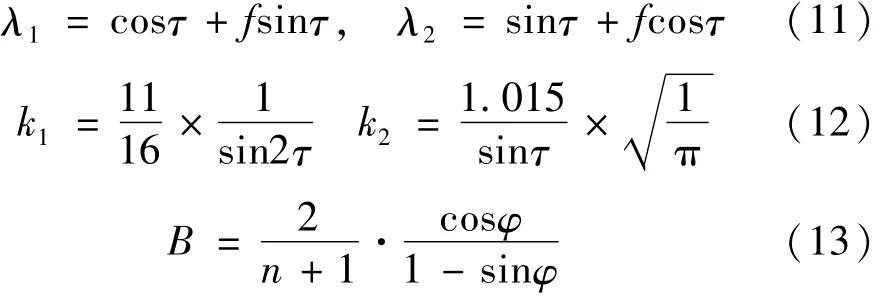
式中:G为岩石剪切弹性模量,ν为泊松比,f为PDC与岩石摩擦系数,A为PDC与岩石接触面面积,c为岩石内聚力,φ为岩石内摩擦角,n为应力分布系数。
PDC片在钻进过程中与岩石的接触面积A是一个周期变化量,与切入角、压入深度和PDC片半径有关,其示意图如图8所示,A为接触弓形面ABD的面积。
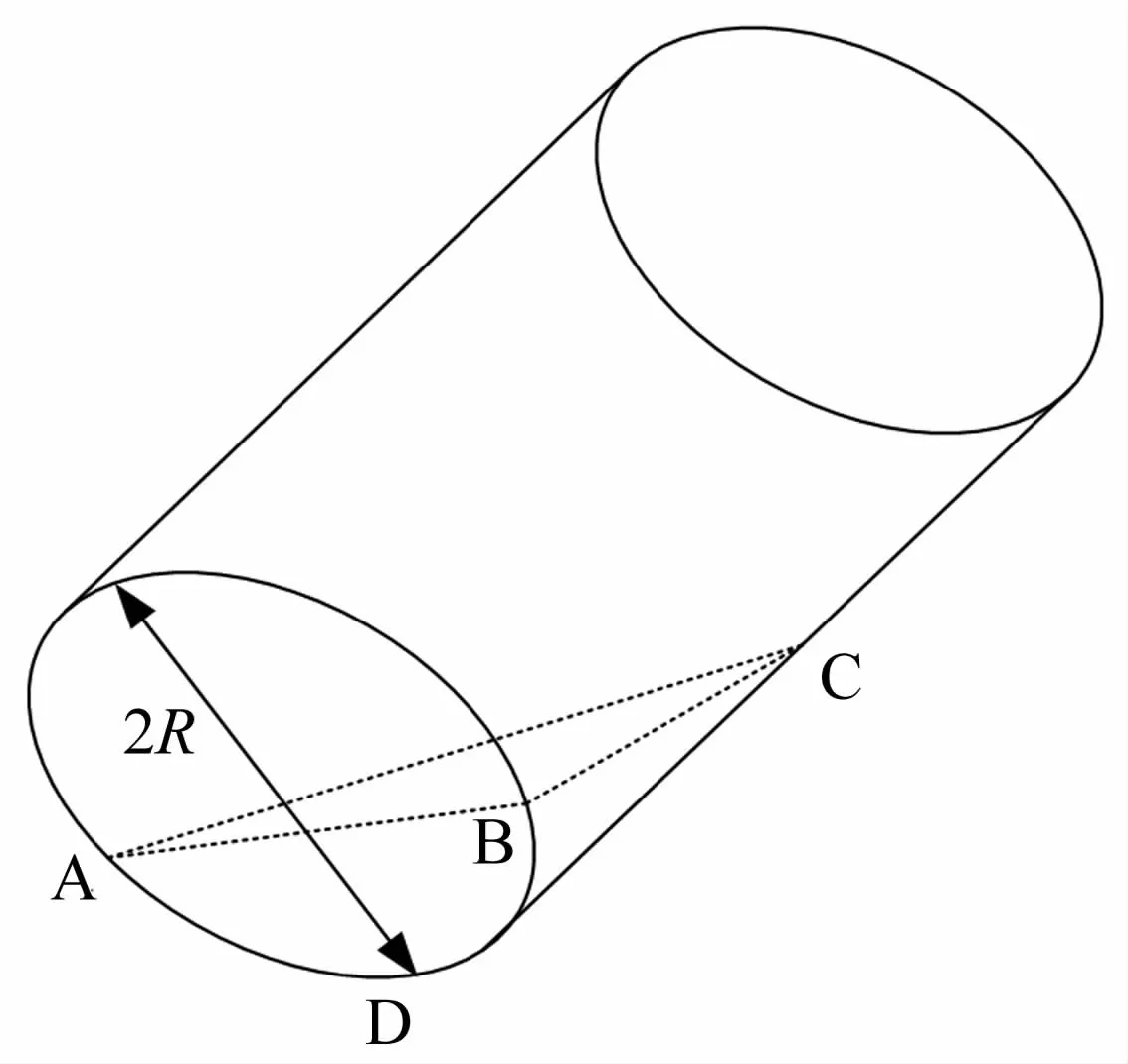
图8 单个PDC与岩石接触面示意图Fig.8 Schematic diagram of a single PDC and rock contact
当弓形面小于半圆面时,这时的面积为:
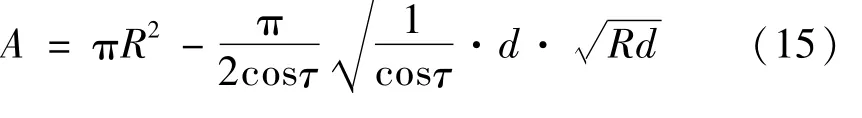
在得到单个PDC片的受力分析之后,就可以推得整个PDC钻头的轴向载荷F和转矩M。

式中:np为PDC片数量,ρ为PDC片中心到钻头中心距离。
因此可以得到钻具所受到的阻力矩如下式所示。剪切力矩:
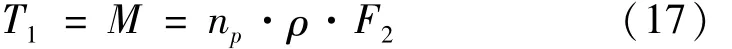
摩擦阻力矩:
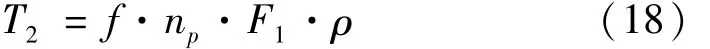
分布阻力矩:

式中:KT是与孔深有关的比例系数。
因为在进行钻进施工时,煤层或岩层的特性是未知的,其弹塑性的变化是很难预测的,因此会给钻头带
当弓形面大于半圆面时,这时的面积为:来复杂多变的工况;另外,钻头在钻进施工时,其轨迹是一个螺旋运动轨迹,故钻头在实际工作过程中受到的是一个复杂多变的变载荷,可将其简化表示为:

PDC钻头设计参数为:钻头外径为96,PDC复合片数量为7片;PDC片半径R为6.75,切入角τ为20°,PDC与岩石摩擦系数 f取0.25~0.5。
假设动力头工作对象为砂岩,其弹性模量G为3.3×1010~7.8×1010,泊松比 ν为0.3~0.35,内摩擦角 φ取45°,内聚力c取30 MPa。
将上述参数代入式(9)至式(20)可以得到转矩的时间历程曲线如图9所示。
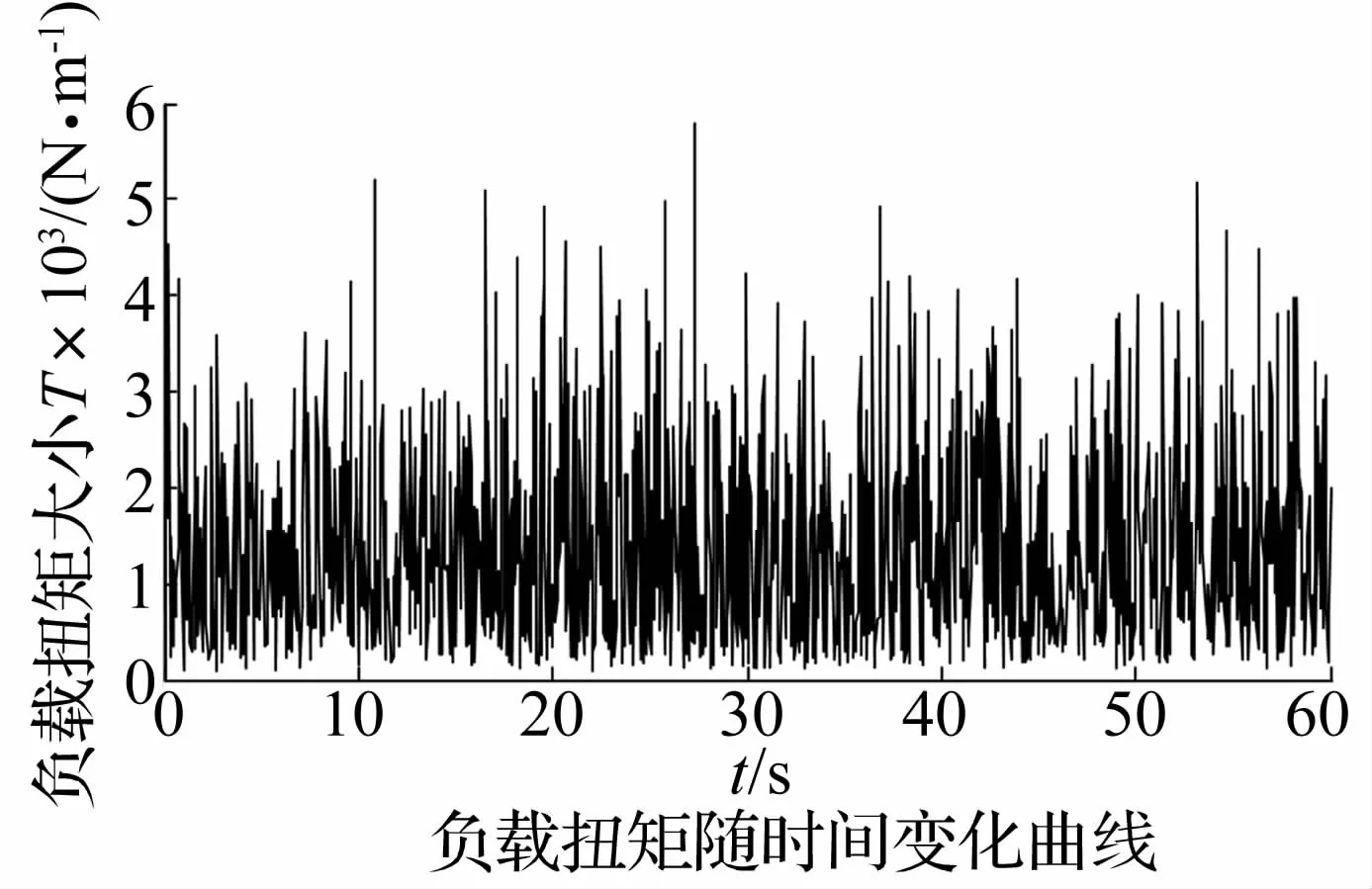
图9 负载扭矩时间历程曲线Fig.9 Load torque of the transmission system
3 动力头传动系统动态特性分析
千米定向钻机动力头齿轮传动系统的设计参数为:高速级:Z1=19,Z2=77,m1=4,β1=12°;低速级:Z3=17,Z4=46,m2=8,β2=12°,输出转速为 40~210 r/min,动力头推进速度为0~1.5 m/min。
在得到动力头齿轮传动系统的时变外部激励和时变内部激励之后,将其代入所建立的齿轮传动系统耦合动力学模型当中利用数值分析方法计算出系统各个构件的动态响应,齿轮g4的动态响应如图10和图11所示。
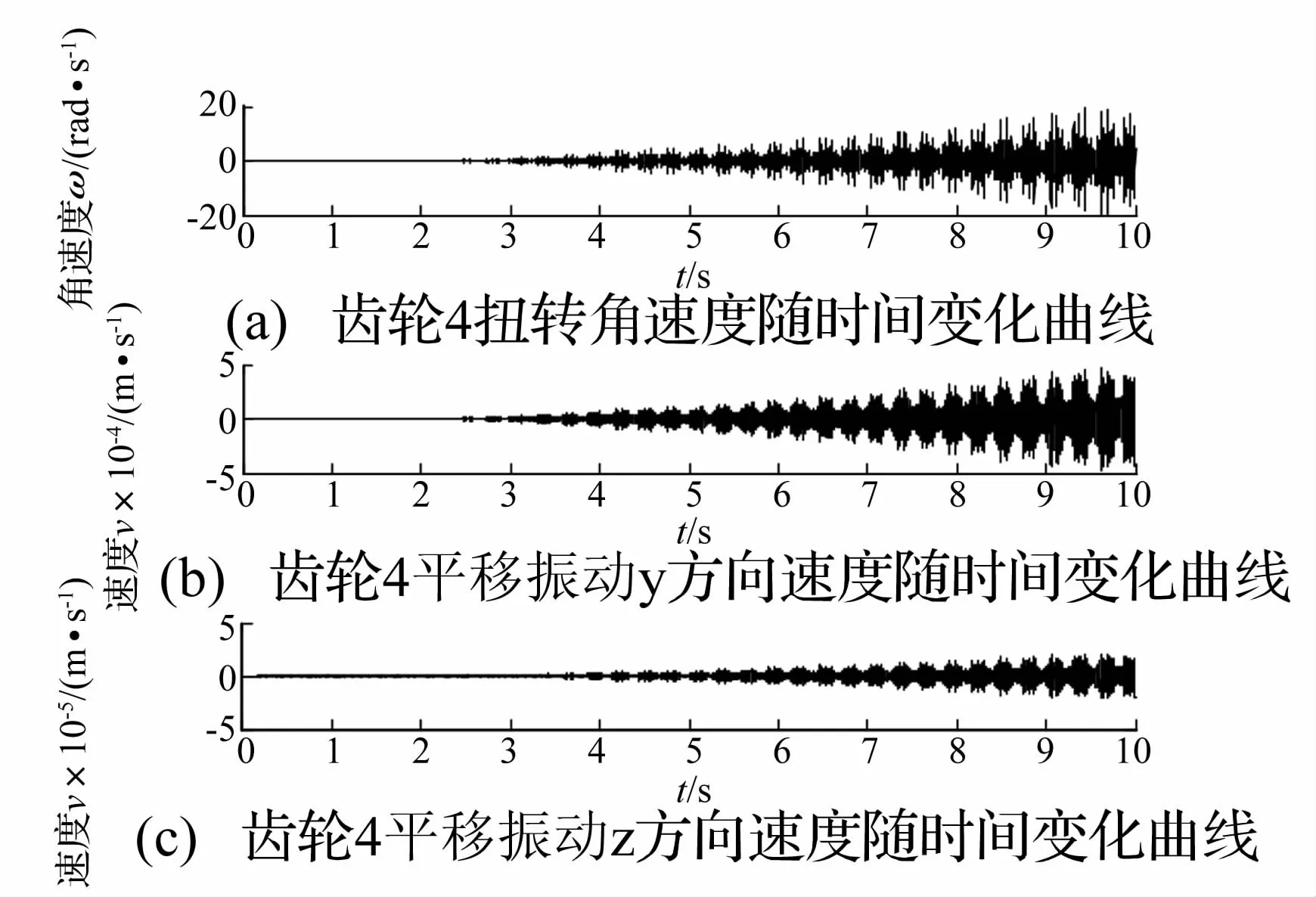
图10 齿轮g4速度动态响应曲线Fig.10 Speed of gear 4 in time domain
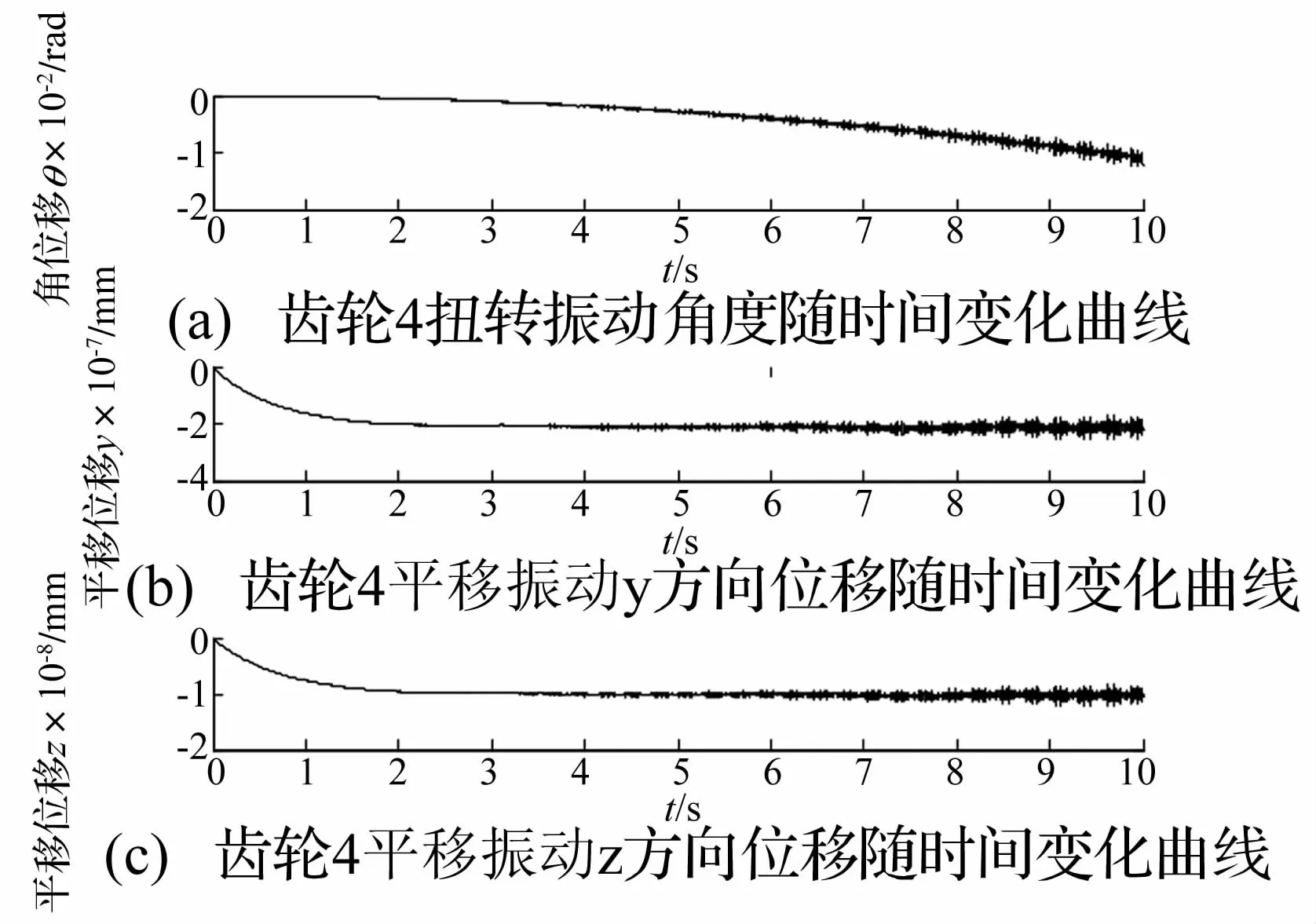
图11 齿轮g4位移动态响应曲线Fig.11 Displacement of gear 4 in time domain
由图10和图11可知:齿轮g4的扭转振动速度响应是关于y=0上下对称的,而平移振动速度响应在经过一段时间后也关于y=0上下对称,且扭转振动幅值远大于平移振动幅值,y向和z向的平移振动速度规律相似;扭转振动位移响应和平移振动位移响应逐渐偏离于y=0轴,并最终趋向于稳定,且二者振动规律相似,而扭转振动幅值也远大于平移振动。
将振动速度响应和振动位移响应以及时变啮合刚度和综合啮合误差代入式(3)和式(4)得到齿轮副的动态啮合力如图12所示。
将其进行快速离散傅里叶变换之后得到其频域曲线如图13所示。

图12 齿轮副g3-g4动态啮合力时间历程曲线Fig.12 Mesh force of the gear pairs in time domain
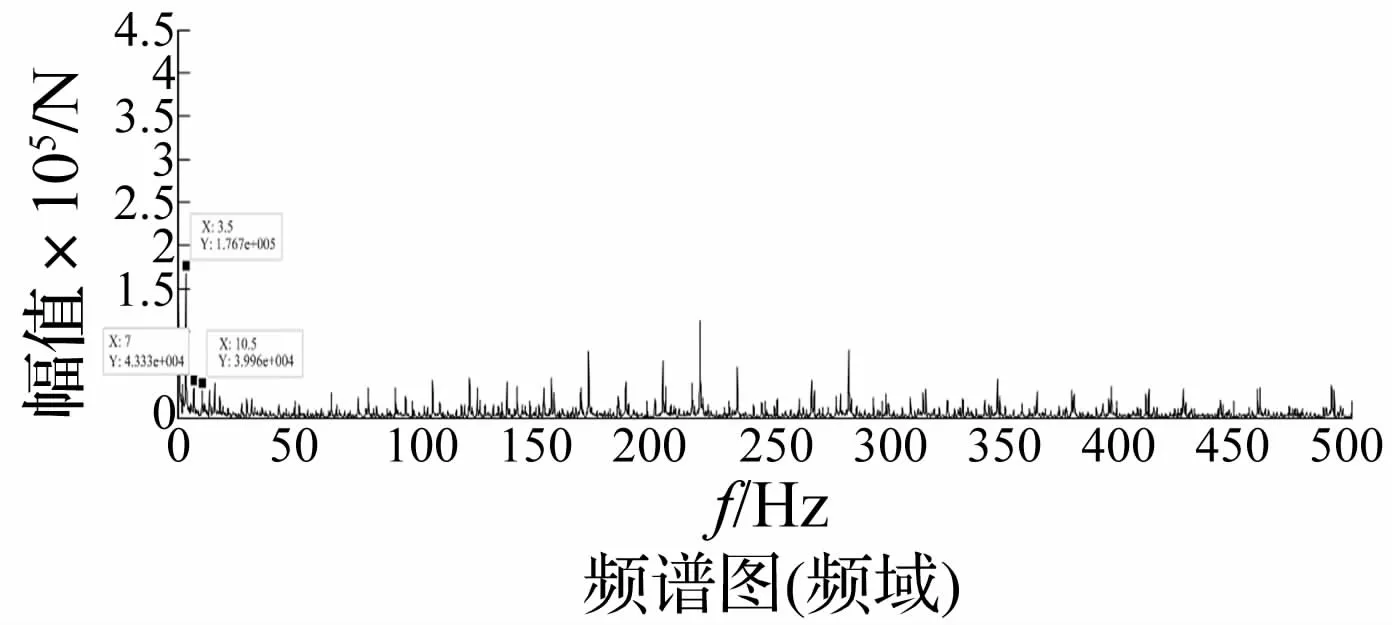
图13 齿轮副g3-g4动态啮合力频域响应Fig.13 Mesh force of gear in frequency domain
由图可知:齿轮副g3-g4动态啮合力振动频率比较复杂,这是由于模型中综合考虑了诸多影响因素。得到啮合力的频谱图后,可以对其作进一步的细化分析得到啮合力各种频率成分,图中给出了齿轮副g3-g4的啮合频率基频点(3.5 Hz)、二倍频点(7.0 Hz)和三倍频点(10.5 Hz)。因为岩石或煤层性质的随机性和不可预测性,造成了钻头负载幅值和频率的复杂性,这是钻机动力头产生振动噪声最主要的因素。
4 结 论
论文在综合考虑钻机动力头的多个时变内部激励和时变外部激励的情况下,利用数值分析方法求解得到了各个构件的动态响应,并最终求得齿轮副的动态啮合力,由本文分析可知:
(1)系统的主要振动表现为扭转振动,因各构件的扭转振动位移幅值相比于平移振动要大很多;各个构件的动态响应规律相似,低频部分与内部激励的变化相关,而高频部分与外部激励相关。
(2)在时变外部激励和时变内部激励共同作用下,系统振动幅值较大,振动频率成分复杂,齿轮间的啮合力也呈现出动态变化且变动幅值较大,其啮合力平均值主要受到负载影响,而振动幅值是内外激励共同作用的结果。
(3)在求得了动态啮合力之后,可以更为准确地估计内部动态系数,为动力头齿轮传动系统的动态优化设计奠定了基础。
[1]Kahraman A,Singh R.Non-linear dynamics of a spur gear pair[J].Journal of Sound and Vibration,1990,142(1):49-75.
[2]Kahraman A,Singh R.Non-linear dynamics of a geared rotor-bearing system with multiple clearances[J].Journal of Sound and Vibration,1991,144(3):469-506.
[3]Lin Jian,Parker R G.Analytical characterization of the unique properties of planetary gear free vibration[J].Journal of Vibration and Acoustics,1999,7(121):13-17.
[4]孙涛,沈允文,孙智民,等.行星齿轮传动非线性动力学建模与方程[J].机械工程学报,2002,38(3):6-10.SUN Tao,SHEN Yun-wen,SUN Zhi-min,et al.Study on nonlinear dynamic behavior of planetary gear train dynamic model and governing equations[J].Chinese Journal of Mechanical Engineering,2002,38(3):6-10.
[5]孙涛,沈允文,孙智民,等.行星齿轮传动非线性动力学方程求解与动态特性分析[J].机械工程报,2002,38(3):11-15.SUN Tao,SHEN Yun-wen,SUN Zhimin,et al.Study on nonlinear dynamic behavior of planetary gear train solution and dynamic behavior analysis[J].Chinese Journal of Mechanical Engineering,2002,38(3):11-15.
[6]秦大同,邢子坤,王建宏.基于动力学和可靠性的风力发电齿轮传动系统参数优化设计[J].机械工程学报,2008,44(7):24-31.QIN Da-tong,XING Zi-kun,WANG Jian-hong.Optimization design of system parameters of the gear transmission of wind turbine based on dynamics and reliability[J].Chinese Journal of Mechanical Engineering,2008,44(7):24-31.
[7]朱才朝,黄泽好,唐倩.风力发电齿轮箱系统耦合非线性动态特性的研究[J].机械工程学报,2005,41(8):203-207.ZHU Cai-chao,HUANG Ze-hao,TANG Qian.Analysis of nonliner coupling dynamic characteristics of gearbox system about wind-driven generator[J].Chinese Journal of Mechanical Engineering,2005,41(8):203-207.
[8]朱才朝,黄琪,唐倩.风力发电升速齿轮箱传动系统接触齿数及载荷分配[J].农业机械学报,2006,37(7):86-89.ZHU Cai-chao,HUANGQi,TANGQian.Study on multi-teeth contact and load distribution of speed increase gearbox transmission system for the wind-driven generator[J].Transactions of the Chinese Society for Agricultural Machinery,2006,37(7):86-89.
[9]朱才朝,陆波,宋朝省.大功率船用齿轮箱系统耦合非线性动态特性研究[J].机械工程学报,2009,45(9):31-35.ZHU Cai-chao,LU Bo,SONG Chao-xing,et al.Research on nonlinear coupling dynamic characteristics of large burden marine gearbox[J]. Chinese Journal of Mechanical Engineering,2009,45(9):31-35.
[10]秦大同,龙威,杨军,等.变风速运行控制下风电传动系统的动态特性[J].机械工程学报,2012,48(7):1-8.QIN Da-tong,LONG Wei,YANG Jun,et al. Dynamic characteristics of wind turbine transmission system under verying wind speed and operation control conditions[J].Chinese Journal of Mechanical Engineering,2012,48(7):1-8.
[11]李田军.PDC钻头破碎岩石的力学分析与机理研究[D].武汉:中国地质大学,2012.
