一阶线性系统随机共振在转子轴故障诊断中的应用研究
2014-09-20冷永刚田祥友
冷永刚,田祥友
(1.天津大学 机械工程学院,天津 300072;2.天津大学 机构理论与装备设计教育部重点实验室,天津 300072)
大型汽轮机、水轮机、燃气轮机等旋转动力机械常工作在高温、高压和高转速等较恶劣的工作环境下,其正常运行对于保证工厂的安全生产意义重大。因此需要对旋转机械进行状态监测,提取振动信号并进行分析以判别是否存在早期微弱故障。但在工程实际中,信号测点往往离故障源较远,使测得的信号容易被强噪声污染,加上早期故障信号本身就比较微弱,这些因素使转子轴的早期微弱故障诊断较为困难。
目前常用的转子轴类故障诊断方法有:基于谐波窗、EEMD滤波的转子轴心轨迹提纯方法[1-2],利用小波或小波包对故障信号进行分解和重构[3]方法,以及基于非线性系统随机共振检测微弱信号的振动分析等[4-6]。这些检测方法各有优点,在一定程度上能反映出转子轴的故障特征,但同时也存在一些局限性。如转子轴心轨迹提纯法步骤较繁琐,测试数据时对硬件设备要求较高;小波或小波包降噪时如何选择阈值和进行阈值优化比较困难;利用非线性系统的随机共振原理降噪时存在系统参数调节等复杂问题。本文以一阶线性系统随机共振方法为基础,通过模型简化,提出一种基于线性系统调参广义随机共振的转子轴类早期微弱故障诊断方法。
1 一阶线性系统的调参广义随机共振现象
很多学者[7-10]关于线性系统随机共振现象的研究都是通过复杂的数学模型推导与仿真得出系统输出存在传统的或是广义的随机共振现象,但这样的系统中信号与噪声的作用方式比较复杂,很难应用于实际故障信号的处理分析中。本文仅针对周期信号加高斯白噪声作用的一阶线性系统中出现的广义随机共振现象[11]能否用于转子轴类早期微弱故障信号的检测进行讨论。
一阶线性系统动力学模型

式中:a是系统参数,输入信号 sn(t)=A sin(2πf0t)+ξ(t),A sin(2πf0t)是频率为 f0、幅值为 A、相位为 0的正弦信号,ξ(t)是功率谱密度为2D的噪声,其中ξ(t)是均值为0,方差为1的高斯白噪声。
求解系统模型(1),得系统输出功率谱密度函数为
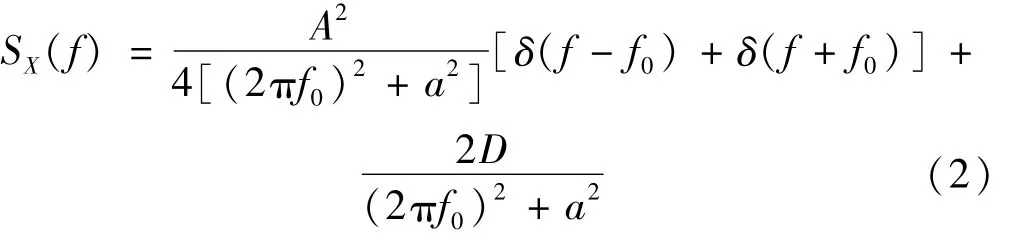
为比较系统输出端信号与噪声的大小关系,引入输出信噪比。这里信噪比的定义采用信号处理及通信等工程实际中常用的信噪比定义,即系统输出端信号总功率与噪声总功率之比[12-13]
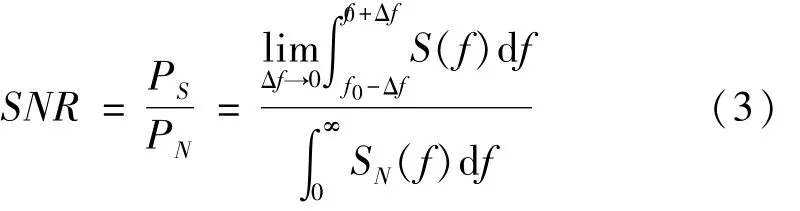
式中:S(f)为输出端信号的功率谱密度函数,SN(f)为输出端噪声功率谱密度函数。

由输出信噪比表达式(4)可以看出,系统参数a不变时,SNRout随噪声强度D单调递减变化,表明周期信号与加性噪声驱动的一阶线性系统中不会出现传统意义上的随机共振现象。但仔细观察式(4)可知,分母中时等号成立),故在噪声强度D不变的情况下,系统参数a取2πf0时,系统输出信噪比取得最大值SNRmax=当输入信号的频率与系统参数取得某种协同匹配关系时,系统输出能够达到共振状态。这种输出信噪比随系统参数非单调变化的现象称之为调参广义随机共振[11]。
下面通过数值模拟验证系统的上述特性,设定一组仿真参数:A=0.1,f0=0.01 Hz,采样频率 fs=5 Hz,计算数据点数N=4 000。用四阶Runge-Kutta方法(以下同)对方程(1)进行数值计算,观察输出信噪比分别随参数D、a的变化趋势,计算结果如图1。算法中的输出信噪比定义为

式(5)是给定计算数据点数条件下的信噪比,其中PS表示输出功率谱中信号总功率,PN表示输出功率谱中噪声总功率。
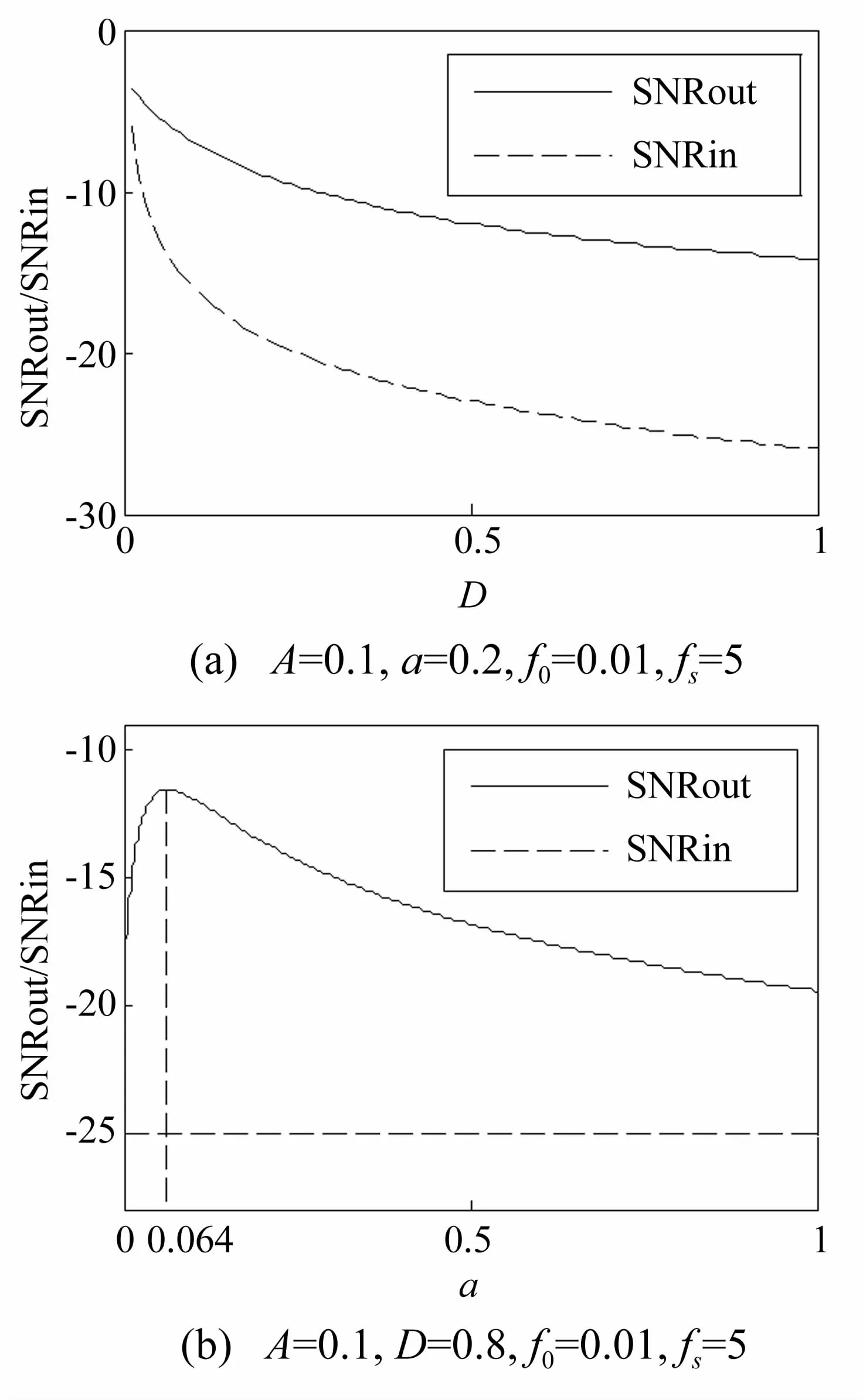
图1 输出与输入信噪比分别随参数D、a的变化趋势Fig.1 The variation tendency of SNRout and SNRin by the parameter D&a.Parameter
同样由图1仿真曲线可以看出,线性系统的输出信噪比随输入噪声强度D单调递减变化,随系统本身参数a非单调变化,存在a值(a=0.064,约等于2πf0)使输出信噪比达到极值。图中虚线表示相应情况下的输入信噪比,其定义为在给定数值分析长度条件下,信号总功率与噪声总功率之比。
2 一阶线性系统调参广义随机共振的微弱信号检测
由前述分析知,在给定输入信号与噪声时,系统取参数a=2πf0输出信噪比达到极大值。为了满足实际工程应用,文献[11]分析了系统参数a=2πf0固定不变情况下,采样频率与信号频率比值对输出频谱的影响,并给出了检测特征信号可辨识性好的比值范围。这表明,实际应用中,使系统输出信噪比最大的参数a值并不一定就能使输出特征信号达到理想的可辨识性,因为信噪比大,只说明系统输出的信号能量与噪声能量比值大,而特征信号的可辨识性与信号幅值、噪声大小以及噪声的分布有关。因此需要进一步分析,实际应用时应如何调节a值才能使特征信号的辨别性最优。下面仿真说明高斯白噪声条件下,输出频谱上特征信号可辨识性与参数a的变化关系。
根据文献[11]比较输出频谱图上特征信号可辨识程度的方法,即提取输出谱图上信号频率处的峰值h,将其与整个谱图上除去信号频率处谱峰后其余谱值中最大的一个值hr作比较,比值越大表明特征信号的可辨识性越好,并将这个比值定义为辨别率r=h/hr.,一般只有r>1时特征信号才容易识别出来。在采样频率与信号频率比值不变的情况下,改变参数a值进行仿真,计算不同a值下输出谱图上特征信号的辨别率r。仿真参数同上:A=0.1,f0=0.01 Hz,D=0.8,采样频率fs=5 Hz,计算数据点数 N=4 000,令参数 a与2πf0的比值在0.1~10之间变化,结果如图2所示。
由图2可以看出,保持采样频率与信号频率比值fs/f0=500不变的情况下,输出谱图特征信号的辨别率r与参数a的取值有很大关系,随a/2πf0比值的变化趋势是先增大至某一极大值,并几乎保持一段水平值,然后再减小,当a/2πf0=4~9时存在一个水平极大值。由此可见选取一个合适的参数a值对特征信号频率的判别有着直接的影响,实际信号检测时应尽量选取使辨别率达到最佳的a值。图3比较了参数a取两个不同值时输出谱图中特征信号的可辨识性,其余参数同图2。

图2 系统输出谱图上特征信号辨别率r随 a/2πf0变化曲线Fig.2 The characteristic signal recognition r changes with a/2πf0 in system output spectrum
由图3可见,图(b)比图(a)的特征信号辨别性明显要好。虽然图(a)中f0=0.01 Hz处的峰值已经是整个谱图上的最大值,但与其附近峰值高度相接近,容易造成误判,而图(b)在f0=0.01 Hz处的谱值明显高于附近其他峰值,很容易确定这就是所寻找的特征信号频率成分。

图3 不同参数a值下系统输出频谱Fig.3 The output spectrum of different parameter a
这里需要指出的是,图2得到的辨别率r随比值a/2πf0变化关系是在采样频率fs与信号频率f0比值保持恒定的情况下得到的,如果改变采样频率与信号频率的比值,那么r随比值a/2πf0的变化关系曲线也会发生变化。为综合分析r随比值a/2πf0和fs/f0的变化关系,图4给出了三者变化关系的三维图。从图4可见,对应于每一组较优的fs/f0值,均可以找到合适的a/2πf0值,使特征信号辨别率r达到最大。另外,应用此方法处理含噪微弱信号时,可不必局限在小频率范围,只要采样频率合适,可以用于检测任意频率大小信号[11]。

图4 特征信号辨别率r随比值a/2πf0和 fs/f0变化三维图Fig.4 The 3D graph of characteristic signal recognition r changes with a/2πf0 and fs/f0
根据以上分析,应用线性系统调参广义随机共振检测实际微弱信号时的步骤可总结为:① 根据已知条件估算故障信号特征频率f0的可能范围,参考特征信号辨别率随比值 a/2πf0和 fs/f0变化的三维图,确定合适的采样频率fs和参数a使信号可识别性最佳。②若输出谱图上信号特征频率不明显,可通过微调参数a的值进行修正或重新确定一组采样频率fs和参数a采样,再次识别计算。
3 转子轴早期微弱故障识别分析
在旋转机械中轴弯曲是一种常见故障,转子轴弯曲是指转轴各截面几何中心连线与旋转轴线不重合,从而使转子产生偏心质量,进而引起不平衡振动。实验在滑动轴承故障试验台上进行,转子轴中心偏离旋转轴线0.38 mm,在试验台远离轴承座向外0.5 m处布置一个加速度传感器,一方面模拟工程实际中由于空间限制无法在轴承座附近布置传感器采集信号的情况,另一方面使故障信号强度进一步衰减,模拟早期微弱故障。
为获得这一早期微弱故障特征信号,利用一阶线性系统调参共振方法进行处理时,首先根据轴的转频和故障类型,判定弯曲故障信号频率f0值,实验中转子轴的转速约为1 700 r/min,则故障信号频率 f0约在28 Hz左右。利用NI数据采集仪和Lab VIEW采集软件进行数据采集,依据特征信号可辨识性最好的采样频率取值原则[11],设置采样频率为 fs=1 kHz,采样点数N=5 000,实测信号的时域波形及低频频谱如图5所示。可知,信号谱干扰成分较多,很难通过直接观察的方法从频谱图上准确判断出故障特征。参考图4取线性系统参数 a=1.1×2πf0,将实测信号输入式(1)系统进行处理,得到图6时频域结果。
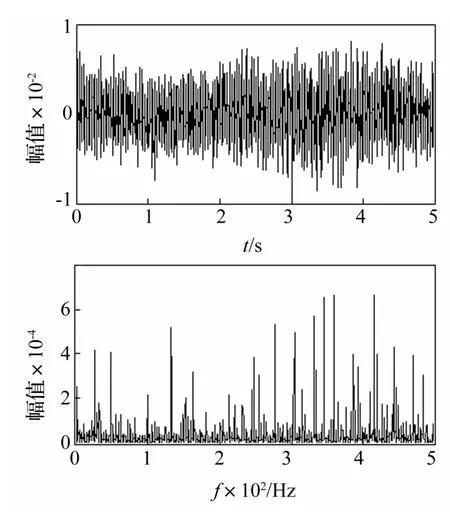
图5 实测转子轴弯曲故障信号的时域图及频域图Fig.5 The time domain and frequency domain of observed rotor shaft bending fault signal
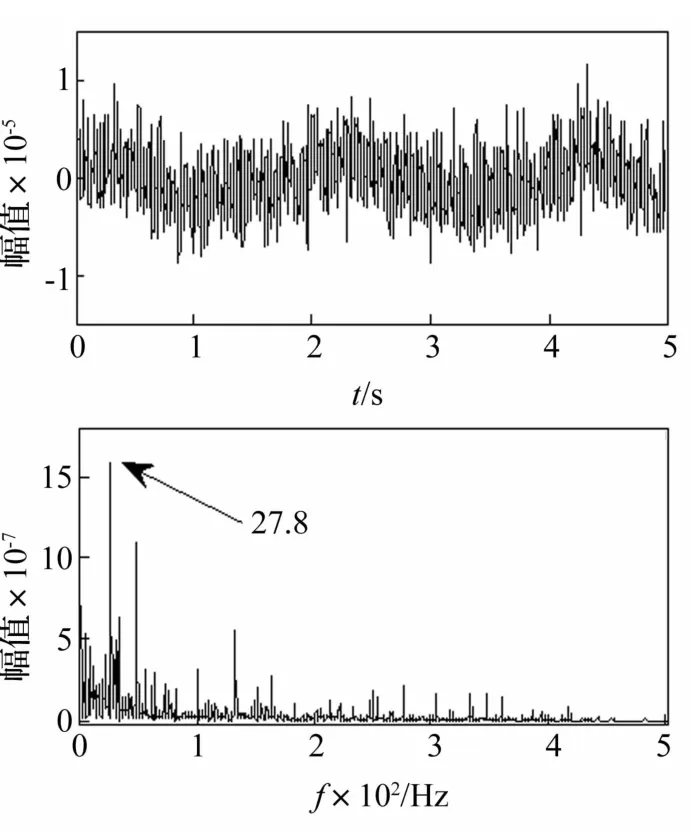
图6 转子轴弯曲故障信号经过线性系统处理后的时域及频域图Fig.6 The time domain and frequency domain of rotor shaft bending fault signal after being processed in linear system
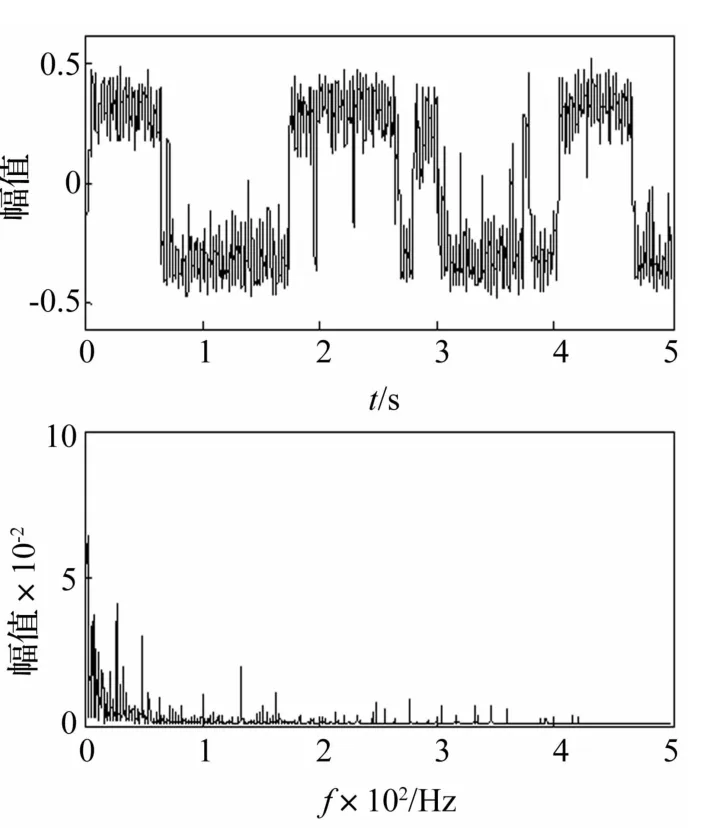
图7 转子轴故障信号经过非线性双稳系统处理后的时域及频域图(参数 a=1,b=10)Fig.7 The time domain and frequency domain of rotor shaft fault signal after being processed in non-linear bistable system.(parameter a=1,b=10)
由图6可以看到,经过处理后输出频谱图上27.8 Hz处有一明显谱峰,且远高于周围其他谱峰,由此识别出滑动轴承转子存在“早期微弱”弯曲不平衡故障。
作为比较,以下采用非线性双稳随机共振方法处理该微弱故障信号[5-6],非线性双稳随机共振检测模型是
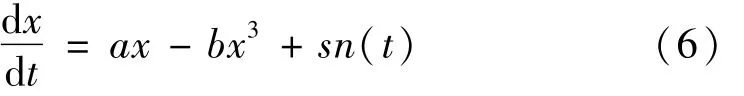
式中:a,b为系统参数,sn(t)为待测含噪信号。将上述实验采集数据代入模型(6)进行处理。由于图5显示信号幅值很低,能量不足以引起粒子在两势阱间的跃迁,所以首先对采集数据进行幅值放大处理,将原始含噪信号幅值同比增大 200倍,即 sn′(t)=200×sn(t)。其次,根据产生随机共振的小参数特性,按照文献[5-6]变尺度方法对原始数据进行二次采样,取二次采样频率 fsr=5 Hz。令参数 a=1,b=10,将经过上述处理的数据代入式(6),用四阶Runge-Kutta法计算,并进行尺度还原得到系统输出时域图和低频频谱如图7所示。
由图7可以看出,在相应参数条件下系统为欠共振状态,频谱图上不易看出明显的特征信号。尝试改变系统参数a=1,b=50,重新计算得到系统输出时域图和低频频谱如图8所示。经过参数的再次调节,图8的频谱可以分辨出故障特征信号成分。
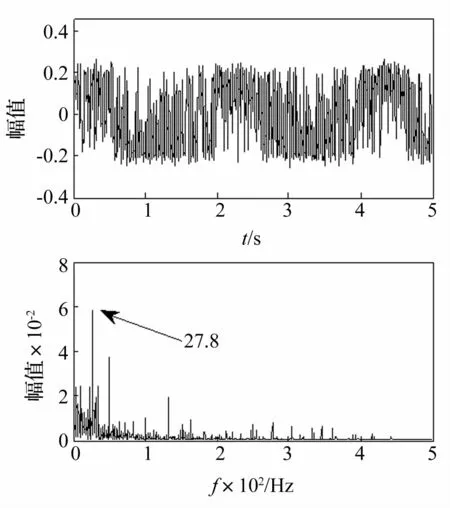
图8 转子轴故障信号经过非线性双稳系统处理后的时域及频域图(参数a=1,b=50)Fig.8 The time domain and frequency domain of rotor shaft fault signal after being processed in non-linear bistable system.(parameter a=1,b=50)
从两种检测方法的对比中可以看出,利用非线性系统随机共振法检测微弱信号时,多参数的协调选择是一个难点,这些参数调节一般需要根据经验选取,多次尝试后才能得到较理想的结果。相比较用一阶线性系统的调参随机共振法检测,采样频率选定后只需要调节系统参数a,就可以得到有效结果,因此该方法在实际应用上更简便有效。
4 结 论
本文研究了一阶线性系统调参广义随机共振机理,及其用于检测微弱故障信号的处理方法。周期信号与高斯白噪声作用下的一阶线性系统,通过调节系统参数,在输出端信噪比能取到极大值,但这并不能保证输出谱图上特征信号能达到理想的识别性。为在输出谱图上得到更清晰的特征信号,文中讨论了信号特征频率的可辨识性与系统参数、信号频率、采样频率等参数之间的变化关系,给出实际应用时各参数取值的参考图。随后滑动轴承试验台上转子轴弯曲故障的实例分析,验证了一阶线性系统调参共振检测早期微弱故障信号的有效性与简便性。
[1]张文斌,周晓军,杨先勇,等.基于谐波窗方法的转子轴心轨迹提纯[J].振动与冲击,2009,28(8):74-77.ZHANG Wen-bin,ZHOU Xiao-jun,YANG Xian-yong,et al.Harmonic window method for purification of axis trace[J].Journal of Vibration and Shock,2009,28(8):74-77.
[2]陈仁祥,汤宝平,吕中亮.EEMD滤波的转子轴心轨迹提纯方法[J].重庆大学学报,2012,35(11):15-20.CHEN Ren-xiang, TANG Bao-ping, L Zhong-liang. A mthod of rotor orbit purification based on ensemble empirical mode decomposition filter[J]. Journal of Chongqing University,2012,35(11):15-20.
[3]杨文志,马文生,任学平.小波包降噪方法在滑动轴承故障诊断中的应用研究[J].噪声与振动控制,2009,29(4):50-53.YANG Wen-zhi, MA Wen-sheng, REN Xue-ping.Application of wavelet packet denoising method in fault diagnosis of bearings[J].Noise and Vibration Control,2009,29(4):50-53.
[4]石鹏,冷永刚,范胜波,等.双稳系统处理微弱冲击信号的研究[J].振动与冲击,2012,31(6):150-154.SHI Peng,LENG Yong-gang,FAN Sheng-bo,et al.A bistable system for detecting a weak pulse signal[J].Journal of Vibration and Shock,2012,31(6):150-154.
[5]Leng Y G,Wang T Y,Guo Y,et al.Engineering signal processing based on bistable stochastic resonance[J].Mechanical Systems and Signal Processing,2007,21:138-150.
[6]冷永刚.双稳调参高频共振机理[J].物理学报,2011,60(2):020503_1-7.LENG Yong-gang.Mechanism of high frequency resonance of parameter-adjusted bistable system [J]. Acta Physica Sinica,2011,60(2):020503_1-7.
[7]Berdichevsky V,Gitterman M.Stochastic resonance in linear systems subject to multiplicative and additive noise[J].Phys.Rev.E,1999,60(2):1494-1499.
[8]Gitterman M.Harmonic oscillator with multiplicative noise:Nonmonotonic dependence on the strengthand the rate of dichotomous noise[J].Phys.Rev.E,2003,67:057103.
[9]张莉,刘立,曹力.过阻尼谐振子的随机共振[J].物理学报,2010,59(3):1494-1498.ZHANG Li,LIU Li,CAO Li.Stochastic resonance in an overdamped harmonic oscillator[J].Acta Physica Sinica,2010,59(3):1494-1498.
[10]陆志新,曹力.输入方波信号的过阻尼谐振子的随机共振[J].物理学报,2011,60(11):110501.LU Zhi-xin,CAO Li.Stochastic resonance of square wave signal in an overdamped harmonic oscillator[J].Acta Physica Sinica,2011,60(11):110501.
[11]田祥友,冷永刚,范胜波.一阶线性系统的调参随机共振研究[J].物理学报,2013,62(2):020505.TIAN Xiang-you, LENG Yong-gang, FAN Sheng-bo.Parameter-adjusted stochastic resonance of first-order linear system[J].Acta Physica Sinica,2013,62(2):020505.
[12]Mitaim S,Kosko B.Adaptive stochastic resonance[J].Proceedings of the IEEE,1998,86:2152-2183.
[13] Gingl Z,Vajtai R,Kiss L B.Signal-to-noise ratio gain by stochastic resonance in a bistable system[J].Chaos,Solitons&Fractals,2000,11:1929-1932.
