基于最近邻域搜索的天线调谐器调谐算法

李引凡

(重庆通信学院信息工程系，重庆 沙坪坝 400035)

基于最近邻域搜索的天线调谐器调谐算法

李引凡

(重庆通信学院信息工程系，重庆 沙坪坝 400035)

介绍了天线调谐器阻抗匹配网络的结构和调谐的本质，提出采用基于启发式算法的邻域搜索算法来解决这一个NP-hard问题;给出了基于固定步长的最近邻域搜索算法的迭代步骤，通过对邻域结构和搜索方式的改进，降低了搜索空间、加快了调谐速度;最后采用基于最近邻域搜索的4种算法对10 m短波鞭状天线进行匹配仿真，验证了改进算法的有效性.

天线调谐器;最近邻域搜索;调谐算法

天线调谐器在短波通信系统中有着非常重要的作用［1］，广泛应用于单兵(背负、便携)式、车载式、机载式、舰载式以及固定式短波电台中(部分中波和超短波电台中也有应用).由于短波天线型式多样、尺寸不一，短波电台功率等级高低不等、频点众多、电磁环境复杂等因素，天线调谐器的重要性尤为突出.

1 天线调谐器匹配网络

天线调谐器主要包括微机控制单元、参数检测单元和匹配网络单元三大部分［2］，其中，阻抗匹配网络主要包括 Γ形、反 Γ形、T形和 П形［3］，如图1 所示.

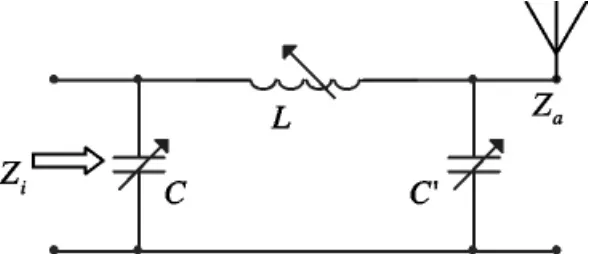
图1 Π形阻抗匹配网络

对于某些频带较窄、天线输入阻抗变化范围特定的情况而言，可仅采用Г形或反Г形网络;而对于频带较宽、天线输入阻抗变化范围巨大的情况而言，需采用T形和П形网络，以覆盖整个阻抗复平面.

1.1 网络参数

匹配网络中的可变电容与可变电感采用多个元件按二进制加权的方式并联或串联并由继电器控制来实现取值的变化，L、C和C'的取值为［4］

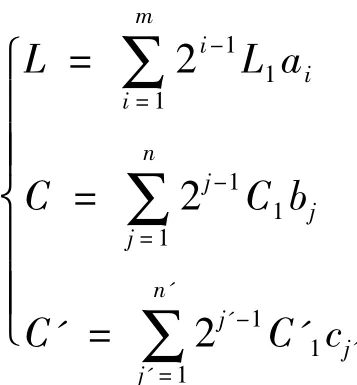
其中，m、n和n'为对应元件阵列的元件个数，i、j和 j'为元件序号，ai、bj和 cj'取值为“0”或“1”，L1、C1和C'1为对应元件阵列的最小元件值.

当ai=bj=cj'=1时表示第i(j、j')个元件接入网络，反之则表示元件与网络断开.这样，L、C和C'就可以分别在0～(2m-1)L1、0～(2n-1)C1和0～(2n'-1)C'1的范围内以L1、C1和C'1为步进任意取值，显然L1、C1和C1'的大小决定了L、C和C'的取值精度.

1.2 网络匹配

天线输入阻抗Za经网络匹配后的输入阻抗Zi为

为了反映匹配网络的匹配性能或最大功率传输性能，可以用反射系数Γ或电压驻波比(Voltage Standing Wave Ratio，VSWR)σ等多个等价的参数来表征，Γ的计算式如下

式中，Rg为源内阻，通常为50Ω或75Ω.在求得Γ后，通过下式可求得σ值:

2 邻域搜索算法

天线调谐器调谐的本质就是在阻抗匹配网络中选择接入或断开恰当的元件，在一定的时间内将VSWR值调整到一个足够小的值，且VSWR值越小越好(理想情况下σ =1)，所用时间越少越好.文献［1］规定的天调调谐速度与精度等级如表1所示.实际应用中，某些战术电台的VSWR容忍值可以为 2，某些大功率电台的VSWR容忍值可以达到3或4.

表1 天调调谐速度与精度等级

虽然理论上网络中各元件的最优组合(VSWR全局最优解)可以通过简单的枚举方法得到，但这只适用于元件数较少的时候.随着元件个数的增加，VSWR可行解的数量(2(m+n+n'))呈指数级增长，因此可以将天线调谐器调谐问题看成一个NP-hard(Non-deterministic Polynomial-time hard，非确定性多项式难题)问题，如果仍通过枚举方法进行VSWR寻优，算法的搜索空间将呈爆炸式增大，需要极长的运行时间与极大的存储空间，在实际应用中通常难以实现.

对于NP-hard问题，一般并不要求一定要得到全局最优解，合理的做法是牺牲一点全局最优性而去寻求有效的、满意的、可行的近似解(如局部最优解).当然，在保证近似解有效性的时候，其全局最优性要尽可能保留.在天线调谐器调谐过程中，由于元件制作工艺、分布参数及电磁兼容等方面的影响，在算法调谐完毕后不可避免地需要进行后期调试，求解全局最优解的意义便大打折扣.

现代计算机科学中解决NP-hard问题的一般方法是采用启发式搜索策略，以期在较短的时间内获得一个很好的局部最优解，邻域搜索就是一种较为通用的启发式搜索策略.

2.1 搜索步骤

邻域搜索是一种简单的、有效的、快速的局部搜索算法，基于局部搜索的算法还包括对分搜索算法、Hooke-Jeeves算法、Powell算法、Simplex算法、Single-Step 算法等［5］.此类方法都是从一个给定的初始点开始，依据一定的方法寻找下一个使目标函数得到改善的更优解，直至满足某种停止准则.

邻域搜索算法从一个初始解(如图2中“○”所示)开始，运用一个邻域产生器，持续地在当前解的邻域(如图2中“●”所示)中搜索比当前解更优的解［6］.若找到比当前解更优的解，则用这个解取代当前解成为新的当前解，继续上述过程，直到在当前解的邻域中找不到更优解为止.

图2 标准邻域搜索

基于图1和图2的邻域搜索算法迭代步骤［7］如下:

⑧则X(k)为最优解.

⑨k=k+1，开始第k=k+1轮迭代.

上述步骤中步长α1、α2和α3为元件最小值时，即α1=L1、α2=C1、α3=C1'，为最近邻域搜索.如果搜索的步长较小，则搜索的效率会降低且容易陷入局部最优解;如果搜索的步长较大，则容易越过全局最优解.

2.2 邻域结构

邻域搜索算法的核心是如何定义一个自然的、优美的、实用的邻域.实践证明，如何定义邻域对计算时间和最后解的质量起着非常重要的作用.

图2所示邻域结构可搜索整个解空间，但当解陷入局部极小值时，即使增大搜索步长也无法跳出.因此，可重新定义“邻域”的概念，使之能克服上述不足.图3给出了两种邻域结构.

(1)图3(a)的邻域结构定义为各坐标轴的边界点，每轮搜索需调用目标函数8次(图2为6次)，然而该邻域只能搜索部分解空间，但当解陷入局部极小值时，增大搜索步长时可跳出;

(2)图3(b)的邻域结构定义为各坐标轴范围内的所有组合点，该邻域结构综合了图2和图3(a)两种类型邻域的优点，但每轮搜索需调用目标函数26次，计算量为前两种的3～4倍，减慢了收敛速度.

图3 邻域结构

2.3 搜索方式

邻域的搜索方式包括并行搜索和串行搜索.2.1中给出的搜索步骤即为并行搜索，即每一轮都对各坐标轴进行搜索，取最优值，再进行下一轮搜索.串行搜索则先在一个坐标轴上进行搜索，直到找到最优值，再在下一个坐标轴上进行搜索，如此反复进行坐标轮换.

串行搜索的优点在于极大地减少了计算量，但串行搜索也存在陷入局部最优解的问题.因此，在邻域结构和搜索方式的选择上，需针对具体的问题而定.图1所示的П形阻抗匹配网络中，C'的作用为将L-C网络匹配区域外的点变换到L-C网络匹配区域内(粗调)，再由L和C完成最后的匹配(细调).这样将L-C和C'分开参与算法，减少了搜索空间，看似搜索效果会更差，实则有所取舍，反而减少了C'参与时局部最优解的影响，不仅搜索速度更快，匹配结果也更好.

2.4 算法仿真

在自适应加速度分离算法中,首先设定一个加速度阈值,假如加速度计测得数据与重力加速度的相差超出该阈值,表示运动产生的加速度对加速度计测量数据产生了一定的影响,此时进行加速度计分离算法。当运动产生的加速度影响较小时,判定条件为:

以SG-230天线调谐器［8］阻抗匹配网络为例，该网络参数配置为:L1=0.25μH、m=8;C1=100 pF、n=6;C1'=25 pF、n'=5.在 2.3～30 MHz范围内取平均分布的485个频点，对10 m鞭状天线进行匹配仿真(通过枚举法求全局最优解可知，SG-230天线调谐器阻抗匹配网络对10 m鞭状天线的适配频段为 f＞2.3 MHz).

根据不同的邻域结构和搜索方式，采用以下4种算法进行仿真:

(1)算法1:图2所示标准最近邻域搜索;

(2)算法2:图3(b)所示最近邻域搜索;

(3)算法3:先利用C'将L-C网络匹配区域外的点变换到匹配区域内，再利用图2所示标准最近邻域在L-C轴搜索;

(4)算法4:先利用C'将L-C网络匹配区域外的点变换到匹配区域内，再利用图3(b)所示最近邻域在L-C轴搜索.

4种算法的匹配结果分布如图4所示，图中虚线为σ=2线，适配性能如表2所示.算法的计算量(对目标函数的调用次数)如图5所示.

图4 算法匹配结果对比

从图4和表2的结果可以看到，算法4是比较符合应用要求的，然而从图5可以看到，4种算法的计算量都分布在数百次量级，这对于调谐时间指标而言显然过于恶劣，这也是最近邻域搜索即单步搜索的缺点.改进的策略包括:

(1)设定可变步长，在搜索成功时增大步长，在搜索失败时减小步长，以此加快搜索的速度;

(2)搜索时只进行单边搜索，即只搜索前进方向;

(3)在调谐初期即远离目标点时，使用其他搜索方式(如对分搜索等)进行粗调，在调谐末期即靠近目标点时使用邻域搜索进行细调.

以上策略的目的是将搜索总次数控制在50次以内，方具有实用价值.

3 结语

目前，直接搜索算法仍是天线调谐器的主流调谐算法，在整个调谐过程中，在不同的阶段需要根据不同的情况选择合适的算法，综合邻域搜索、对分搜索等方式的优点，以使得算法尽快收敛于VSWR门限内.调谐速度和匹配精度始终是矛盾的两面，如何在两者间取得折中以满足应用的需求，是值得进一步深入研究的问题.

［1］SJ-20489-1995.中华人民共和国电子行业军用标准——天线调谐器通用规范［S］.1995.

［2］胡中豫.现代短波通信［M］.北京:国防工业出版社，2003:179-182.

［3］李引凡，卜鑫，彭焰.天线调谐器Γ形/反Γ形阻抗匹配网络参数估算［J］.重庆通信学院学报，2013，32(1):20-23

［4］Li Y F.Parameters computation of T-section impedance matching network of antenna tuner［C］.The 3rd International Conference on Mechanic Automation and Control Engineering，2012(1):413-416.

［5］Sunghoon O.Automatically tuning antenna system for software-defined and cognitive radio［D］.Arizona State University，2006.

［6］Li Y F，Zhang YW，Qiu H Y，etal.Fast tuning algorithm of HF-VHF antenna tuner based on neighbor searching［C］.The 2nd International Conference on Mechanic Automation and Control Engineering(MACE 2011)，2011:4073-4076.

［7］刘惟信.机械最优化设计:第2版［M］.北京:清华大学出版社，1994.

［8］SG-230 Smartuner Antenna Coupler:Installation and Operations Manual［R］.SGC Inc，2000.

(责任编辑 吴 强)

Tuning algorithm of antenna tuner based on nearest neighbor searching

LIYinfan

(Department of Information Engineering，Chongqing Communication College，Shipingba Chongqing 400035，China)

The structure of impedancematching network and the essence of tuning algorithm in antenna tuner are introduced，and the heuristic algorithm called neighbor searching algorithm is proposed to solve the NP-hard problem.Then the iteration steps of nearest neighbor searching algorithm with fixed step size is described in detail which are applied to antenna tuner，and the algorithm is improved by different neighbor structures and searching patterns，so the searching space is reduced and the tuning speed is accelerated.At last four tuning algorithms based on nearest neighbor searching are simulated with a 10m HF whip antenna and the validity of the improved algorithm is certified.

antenna tuner;nearest neighbor searching;tuning algorithm

TN820.8

A

1673-8004(2014)05-0053-05

2013-12-10

李引凡(1979-)，男，重庆市人，讲师，主要从事军事无线通信技术与装备方面的研究.