基于Gibbs-DA算法的贝叶斯分位回归模型研究*

朱慧明，翁 元，曾昭法，任英华，李招来

(1．湖南大学 工商管理学院，湖南 长沙 410082；2．湖南大学 金融与统计学院，湖南 长沙 410079)

回归分析模型是实践中应用广泛的一类统计模型，如果模型中的随机扰动项来自均值为零而且同方差的分布，回归系数的OLS估计具有最佳线性无偏性,并且，如果随机扰动项服从正态分布，回归系数的OLS估计量和ML估计为最小方差无偏估计．但是，在现实社会经济系统中，这些假设条件通常难以得到满足，例如，数据可能出现尖峰或厚尾分布和异方差等问题，此时OLS估计量不再具有上述优良性．为了弥补OLS估计方法的不足之处， Koenker和Bassett[1]提出了分位回归模型的建模思想．与OLS方法相比，分位回归通过加权误差绝对值之和最小化方法得到参数的估计，这些估计量不容易受到异常值的影响，稳健性强．分位回归模型在金融风险度量、时间序列和生存分析等领域中获得了广泛应用[2-5]．

分位回归模型参数估计方法很多，例如，对偶单纯形估计算法、内点法和外点法等．但是，它们是建立在经典统计理论基础之上，参数是固定不变常数．为了考虑参数不确定性问题，Yu和Moyeed[6]，Tony和Sung[7]，Tsionas[8]和曾惠芳[9]等利用MCMC抽样方法构建贝叶斯分位模型．但是，它们没有研究模型参数的随机抽样问题．本文利用Gibbs抽样和数据扩展(Data Augmentation，DA)算法，构建基于Gibbs-DA抽样算法的贝叶斯分位回归模型，解决模型参数不确定性风险问题．

1 非对称Laplace分布的混合表示

定义1如果随机变量U具有如下密度函数：

(1)

则称U服从位置参数μ，尺度参数σ和偏度参数τ的非对称Laplace分布，记作U～ALD(μ,σ,τ)．特别地，当μ=0,σ=1时，记作U～ALD(τ)．如果随机变量U服从非对称Laplace分布ALD(μ,σ,τ)，则它的数学期望和方差如下：

U的特征函数为:

(2)

非对称Laplace分布与指数分布、正态分布之间存在密切关系：服从非对称Laplace分布的随机变量可以用指数分布、正态分布的随机变量的函数来表示．如果U1,U2分别服从指数分布Exp(1)和正态分布N(0,1)，并且两者相互独立，记:

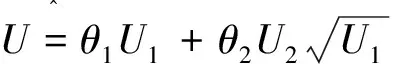
(3)

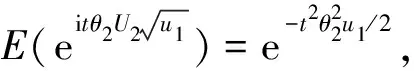
(4)

这就是μ=0,σ=1时非对阵Laplace分布的特征函数．根据特征函数的唯一性定理可知：U～ALD(τ)．

2 贝叶斯分位回归算法

假设y与p维变量x之间具有线性函数关系：

y=x'β+ε

(5)

此处β=(β1,β2,…,βp)'，随机误差项ε的概率分布函数为F．显然，对于给定的x，随机变量y的τ分位数等于x'β+F-1(τ)，即:

Qy(τ|x,β)=x'β+F-1(τ)

(6)

其等价形式为:

Qy(τ|x,β(τ))=x'β(τ)

(7)

此处β(τ)=(β1(τ),β2(τ),…,βm(τ))'，也就是说，β(τ)与分位数τ的取值大小有关．

假设(x1,y1),(x2,y2),…,(xn,yn)是(x,y)的一组观察值，则β(τ)的估计为:

(8)

其中ρτ(u)=u(τ-I(u<0))为损失函数，I(u<0)为示性函数．由于

(9)

等价于

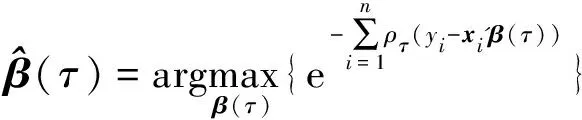
(10)

而后者恰好是非对称Laplace变量的联合分布密度函数的核，因此，根据非对阵Laplace分布的性质，分位回归建模问题可以进一步转化为

i=1,2,…,n

(11)

中的参数β(τ)；此处zi,ui相互独立，zi服从标准指数分布Exp(1)，ui服从标准正态分布；模型(8)称为数据扩展模型，zi称为潜变量(latent variable)．

则模型(8)可以简化为如下矩阵形式：

(12)

L(Y|X;Z,β(τ))

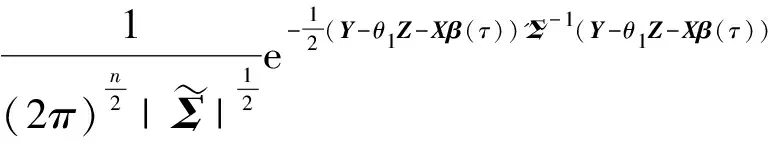
(13)

由于Z的分量相互独立，并且均服从标准指数分布Exp(1)，其概率分布密度函数

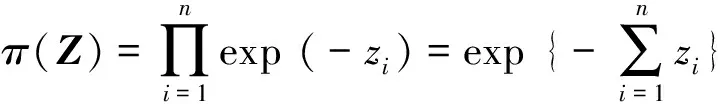
(14)

为了进行贝叶斯分析，需要进一步设置分位回归模型参数的先验分布．根据文献[10]的观点，选择如下均值向量β0，协方差阵Σ0的多元正态分布作为模型参数β(τ)的先验分布，即

β(τ)～Np(β0,Σ0)，β0∈Rp,Σ0>0

(15)

此处β0,Σ0可以由Koenker的经典分位回归方法确定．根据贝叶斯定理，潜变量和参数的后验分布密度与似然函数、先验分布密度的乘积成正比，即:

(16)

为了能够进行MCMC抽样算法，研究潜变量和参数完全条件后验分布．

1)参数β(τ)的完全条件后验分布．通过π(β(τ),Z|Y,X)关于β(τ)的积分运算，获得Z的边缘后验分布密度函数π(Z|Y,X)，据此计算β(τ)的完全条件后验分布密度函数π(β(τ)|Y,X'Z)．不难验证：参数β(τ)的完全条件后验分布密度函数为

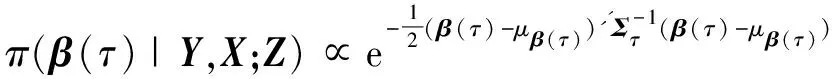
(17)

显然，β(τ)的完全条件后验分布是均值μβ(τ)，协方差阵Στ的正态分布，即

(β(τ)|Y,X;Z)～Np(μβ(τ),Στ)

(18)

2)潜变量U的完全条件后验分布．同样地，通过π(β(τ),Z|Y,X)关于Z的积分运算，求出参数β(τ)的边缘后验分布密度函数π(β(τ)|Y,X)，据此进一步计算Z的完全条件后验分布密度函数π(Z|Y,X;β(τ))．对于给定的Y,X和β(τ)，Z的完全条件后验分布密度函数为:

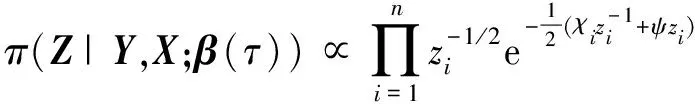
(19)

(zi|Y,X;β(τ))～GIG(1/2,χi,ψ),

i=1,2,…,n

(20)

其分布密度函数为

π(Z|Y,X;β(τ))

其中

根据潜变量Z和模型参数β(τ)的完全后验条件分布，确定贝叶斯分位回归模型的MCMC抽样步骤：

Step 1．设置参数β(τ)的初始值β(0)(τ)，以及样本量lN．并且，假设(Z(j-1),β(j-1)(τ))为(Z,β(τ))的第j-1次抽样结果;

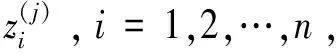
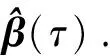
以上是基于Gibbs-DA抽样的单链条算法．当然，为了便于分析Markov链的平稳性，也利用Gibbs-DA抽样同时生成β(τ)的多条链．例如，给定β(τ)的m个初始值{β(i0)(τ),i=1,2,…,m}，生成如下m个长度为lN的Markov链：

然后，根据Gelman-Rubin收敛诊断检验统计量分析Markov链{β(ij)(τ),i=1,…,m；j=1,…,lN}的收敛性问题．如果Gelman-Rubin检验统计量的取值介于1.0到1.2之间，则链条达到平稳状态，此时利用样本{(Z(i, lj),β(i, lj)(τ)),i=1,2,…,m；j=M+1,M+2,…,N}，对模型参数进行统计推断，求出模型参数点估计及置信水平1-α的区间估计，并对模型进行拟合分析．

3 实证研究

作为上述方法的应用，我们考虑我国历年能源消耗弹性的贝叶斯分位回归问题．模型变量包括能源消耗总量(y，单位：万吨标准煤)、国内生产总值(GDP，单位：亿元)，以及第二产业所占比重(P，单位：%)数据研究．数据来源于历年 《中国统计年鉴》、《中国能源统计年鉴》，涉及全国30个省市自治区(不含西藏)，同时，为了便于比较分析，GDP数据按2005年价格计算．能源消耗总量、国内生产总值和第二产业所占比重之间存在如下关系：

ln (y)=β0+β1ln (GDP)+β2ln (P)+ε

此处P=GDP2/GDP×100；β1表示能源消耗的GDP弹性系数，而β2为能源消耗的产业结构弹性系数．

首先，利用2010年全国30个地区的数据，分别建立3个分位点(τ=0.25，0.50和0.75)的贝叶斯分位回归模型．为此，运用Quantreg初步估计分位回归模型系数，并将估计结果作为贝叶斯分位回归模型参数先验分布的均值向量；同时，参数先验分布的协方差矩阵如下：Σ0=diag(1 000,1 000,1 000)．为获得模型参数的贝叶斯估计，通过运用R2WinBUGS软件，对每个参数模拟生成两条Markov链，每条Markov链的迭代次数均为100 000次，以确保Markov链的收敛性．在MCMC模拟初始阶段，Markov链取值可能与参数的初始值选择有关，为此，舍弃每条链的前50 000次抽样结果，利用余下的50 000次数据进行统计分析．表1给出了分位回归模型系数的贝叶斯估计结果．

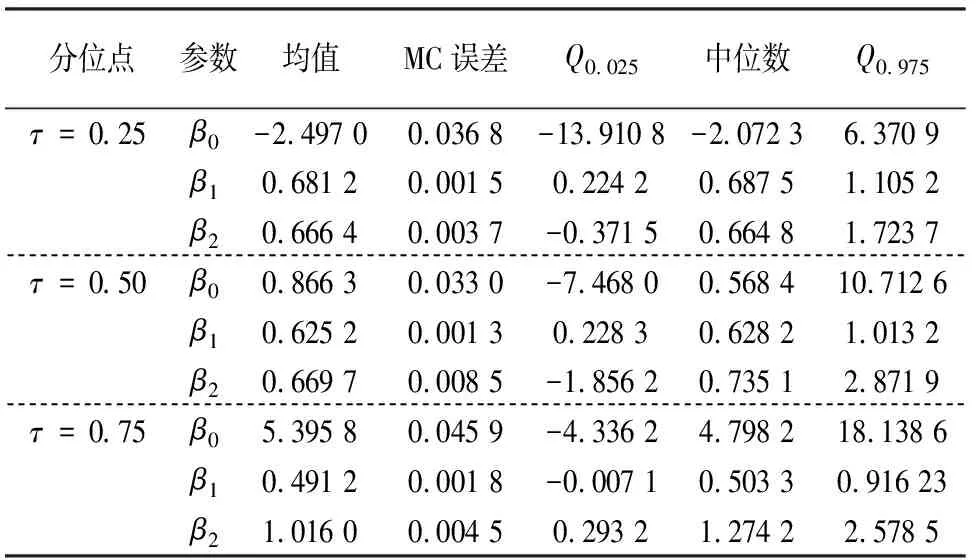
表1 分位回归模型参数的贝叶斯估计结果

根据表1所列出的计算结果，0.25分位点的GDP弹性系数为0.681 2，也就是说，在产业结构保持不变的条件下，GDP增加大于1%，能源消耗总量增加0.681 2%；0.75分位点的GDP弹性系数为0.491 2，低于0.25分位点的估计值；与能源消耗的GDP弹性系数情况不同，0.75分位点的产业结构弹性系数的取值为1.016 0，大于0.25分位点的产业结构弹性系数．为了能够从时间维度和不同分位点两个方面分析能源消耗总量与GDP、产业结构之间的关系，利用2001-2009年的统计数据，根据前面的建模思路，进一步构建0.25，0.50和0.75三个分位点的贝叶斯分位回归分析模型，合计27个模型．

表2汇总了2001-2010年能源消耗的GPD弹性系数，即：30个分位回归模型系数 的估计，该表最后一列等于(β1(0.25)-β1(0.75))/β1(0.75)×100. 从时间维度来看，2001-2010年3个分位点的GDP弹性系数变化不大，但是，0.75分位点的GDP弹性系数明显小于0.25分位点的弹性系数．由于0.75分位点代表能源消费量较高的地区，主要是东部地区；而0.25分位点代表能源消费量低的地区，主要是中、西部地区．这说明我国东部整体单位经济增长所消耗的能源少于中、西部整体单位经济增长所消耗的能源，东部的能源利用率和节能力度优于中、西部.

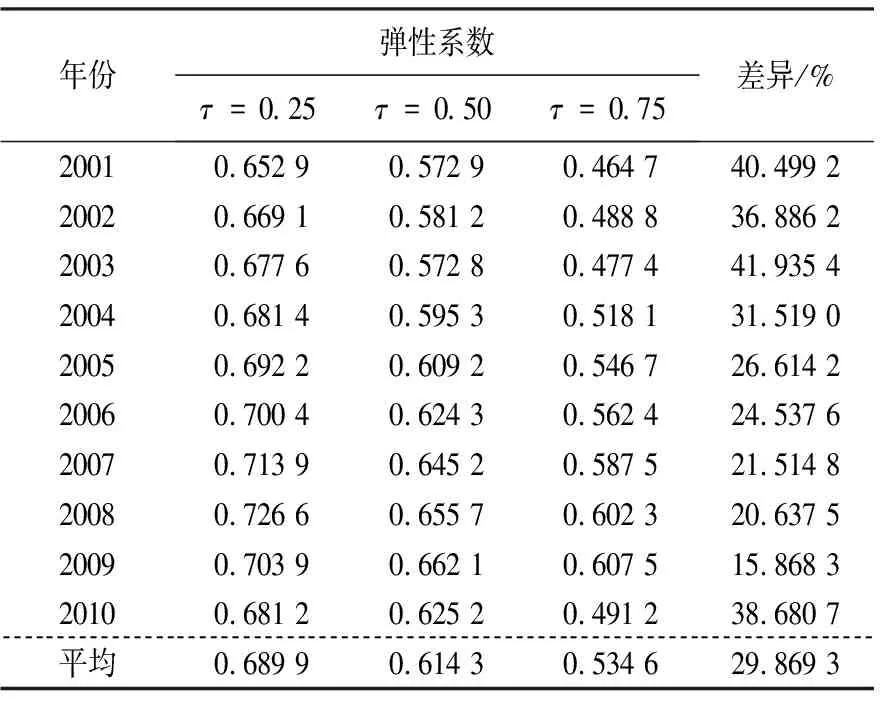
表2 2001-2010年能源消耗的GDP弹性系数

表3汇总了2001-2010年能源消耗的产业结构弹性系数，即：30个分位回归模型系数β2的估计，该表的最后一列等于(β2(0.75)-β2(0.25))/β2(0.25)×100. 从时间维度来看，2001-2010年三个分位点的产业结构弹性系数下降趋势明显，但是，与GDP弹性系数情况不同，0.75分位点的产业结构弹性系数大于0.25分位点的弹性系数．这说明2001-2010年东部的高产出相对西部来说是依靠高能耗实现的．

表3 2001-2010年能源消耗的产业结构弹性系数

4 结 论

本文讨论了贝叶斯线性分位回归模型的构建、MCMC仿真分析及其应用问题．通过模型的统计结构分析，根据非对称Laplace分布的正态—指数分布的混合表示性质，利用服从指数分布的潜变量，据此获得模型的似然函数，推断了多元正态先验分布条件下分位回归模型参数的后验分布，证明了潜变量的完全条件分布为广义逆高斯分布．在此基础上，根据MCMC仿真分析思想，设计了贝叶斯分位回归模型的Gibbs-DA随机抽样步骤及统计分析．利用我国2001-2010年期间各地区的能源消耗总量，GDP和产业结构数据进行实证分析，研究结果表明，贝叶斯方法可以有效地应用于分位回归建模问题．

[1]KOENKER R, BASSETT G. Regression quantiles[J]. Econometrica, 1978, 46(1): 33-50.

[2]WOLTERS M H. Estimating monetary policy reaction functions using quantile regressions[J]． Journal of Macroeconomics, 2012, 34(2): 342-361.

[3]BAUR D G , DIMPFL T, JUNG R C. Stock return autocorrelations revisited: A quantile regression approach[J]. Journal of Empirical Finance, 2012, 19(2): 254-265.

[4]FITZENBERGER B F, KOENKER R, MACHADO J A F. Economic applications of quantile regression[M]. Heidelberg: Sprink, 2002：135-148.

[5]罗幼喜,田茂再.面板数据的分位回归方法及其模拟研究[J]. 统计研究, 2010, 27(10): 81-87.

LUO You-xi,TIAN Mao-zai. Quantile regression for panel data and its simulation study [J]. Statistical Research, 2010, 27(10): 81-87.(In Chinese)

[6]YU K M, MOYEED R A. Bayesian quantile regression[J]. Statistics & Probability Letters, 2001, 54(4): 437-447.

[7]TONY L, SUNG J J. Bayesian quantile regression methods[J]. Journal of Applied Econometrics, 2010, 25(2): 287-307.

[8]TSIONAS E G. Bayesian quantile inference[J]. Journal of Statistical Computation and Simulation，2003，73(9): 659 - 674.

[9]曾惠芳，朱慧明，李素芳，等．基于MH算法的贝叶斯分位自回归模型[J]．湖南大学学报:自然科学版，2010，37(2)：88-92.

ZENG Hui-fang, ZHU Hui-ming, LI Su-fang,etal．Bayesian inference on the quantile autoregressive models with MH algorithm[J]. Journal of Hunan University: Natural Sciences, 2010，37(2)：88-92. (In Chinese)

[10]ALHAMZAWI R, YU K M. Power prior elicitation in bayesian quantile regression[J]. Journal of Probability and Statistics, 2011, 3(1): 1-16.