基于两阶段Expectile回归的风险保费定价
2024-03-02郭哲琦高苏浩
郭哲琦,高苏浩
(中国人民大学统计学院,北京 100872)
0 引言
风险保费由纯保费和风险附加构成。纯保费通常使用广义线性模型进行厘定,而风险附加通过各种保费原理进行计算。在厘定纯保费的广义线性模型中,既可以分别建立索赔频率和案均赔款的预测模型,将两者相乘即得纯保费的预测值;也可以分别建立出险概率和累积赔款的预测模型,将两者相乘求得纯保费的预测值。在纯保费的基础上,再应用期望值保费原理或标准差保费原理计算风险保费。这种定价方法在风险保费的计算过程中,需要人为设定风险附加系数,存在一定的主观任意性。Heras 等(2018)[1]提出应用分位回归计算风险保费,也被称作分位数保费原理。在这种方法中,将风险保费看作一个整体,用分位回归进行预测。应用分位回归计算风险保费的基本原理是把实际赔款超过风险保费的概率控制在一个合理的水平上,比如不超过0.1%。从分位回归计算的风险保费中减去纯保费也可以分离出风险附加。与传统的广义线性模型相比,应用分位回归计算风险保费具有一定优势[2]。但是在应用分位数保费原理时,仍然需要人为设定分位数水平,比如将95%的分位数作为风险保费。这种设定分位数水平的方法可能导致保单组合在总体上的风险保费偏离实际需要。在分位回归中,如果将分位数水平设定为50%,那么就会得到分位回归的特例,即中位数回归。在费率厘定中风险保费的分位数水平通常大于50%,应用分位回归厘定风险保费相当于在中位数的基础上计算风险附加,这与风险保费的概念不是十分吻合。此外,保险损失往往是右偏的,具有较长的右尾,中位数远小于均值(即纯保费),分位数对尾部数据并不敏感,这使得分位数保费原理在定价逻辑上不是十分合理。
基于已有研究,本文提出了期望分位数[3](Expectile)保费原理,即应用期望分位回归代替分位回归厘定风险保费。在50%的分位数水平上,期望分位回归等价于均值回归,因此,应用期望分位回归厘定风险保费,相当于在均值(亦即纯保费)基础上计算风险附加,这与风险保费等于纯保费与风险附加之和的定义在逻辑上完全吻合;此外,期望分位数不仅与损失发生概率相关,而且与损失金额有关,因此用期望分位数计算风险附加更加合理。无论是在广义线性模型的基础上应用期望值原理或标准差原理计算风险保费,还是直接应用分位回归或期望分位回归计算风险保费,都需要确定风险附加系数或分位数水平。现有文献在研究中都是人为给定一个具体数值,如将分位数水平设定为95%,缺乏客观依据。为此,本文提出一种自上而下的定价思路,在控制保单组合总体风险水平的基础上,比如要求保单组合的总赔款超过总风险保费的概率小于0.1%,通过Bootstrap 方法计算出保单组合的总风险保费,然后再将其分解到个体保单上,要求保单组合的总风险保费等于个体保单的风险保费之和,从而提供了一种基于实际数据计算风险附加系数或分位数水平的新思路。
1 分位回归与函数系数分位回归
假设随机变量Yi的分布函数为FYi(y),对于[0,1]区间内任意一个分位数水平τ,随机变量Yi的τ分位数q(τ)定义如下:
在分位回归中,假设因变量Yi的τ分位数q(τ|xi)与协变量xi的关系可以表示为:
其中,xi=(1,xi1,xi2,…,xim)T,i=1,2,…,n,n为样本量,m为协变量维数,回归系数向量β(τ)可以通过最小化下述非对称线性损失函数求得[4]:
最小化式(3)的一阶条件为:
即:
式(5)表明分位数q(τ|xi)与Yi的具体取值无关,对极端值不敏感,这可能导致低估尾部风险,从而影响风险保费的合理性。
传统分位回归的预测值在相邻分位数之间可能出现交叉现象,即不同分位数水平上的预测值可能是相同的,这会造成相互矛盾的结果,为此,Frumento 和Bottai(2016)[5]提出了一种函数系数分位回归,即将回归系数表示为分位数水平τ的函数:
其中,b1(τ),…,bh(τ)是关于τ的给定函数,b0(τ)一般设置为1,γj=(γj0,γj1,···,γjh),γjk(k=1,…,h)是给定函数的系数。
函数系数分位回归的一般形式如下:
如果令h=2,那么式(7)中的Γ 和b(τ)可以表示为[6]:
最小化下述损失函数,即可求得函数系数分位回归的参数估计值:
2 期望分位数与期望分位回归
类比分位数q(τ),Newey和Powel(l1987)[7]提出了期望分位数Q(τ)。对于给定的分位数水平τ,随机变量Yi的期望分位数Q(τ)的定义如下:
其中,I(·)是示性函数。
在风险管理中,分位数称作VaR 风险度量。类似地,Kuan 等(2009)[8]将期望分位数称作EVaR 风险度量[9]。分位数VaR 不满足风险度量的一致性要求,而期望分位数EVaR 不仅满足风险度量的一致性要求,即具有平移不变性、单调性、正齐次性和次可加性,而且具有许多其他良好性质[7,10]:
(1)EVaRτ是分位数水平τ的严格单调增函数,τ∈(0,1)。
(2)EVaRτ是Yi的严格单调增函数,即Yi′≥Yia.s.且。
(3)EVaRτ(-Yi)=-EVaRτ(Yi)。
(4)若Yi关于y对称,则EVaRτ(Yi)+EVaR1-τ(Yi)=2y。
(5)EVaRτ具有可引出性(Elicitability),即通过最小化目标函数可以求得EVaR风险度量[11]。
可以证明,只有EVaR是同时满足一致性和可引出性的风险度量[12]。
EVaR 不仅具有良好的理论性质,而且在风险管理中也有较为直观的解释。可接受域是理解风险度量的另一种常见形式。譬如,若将可接受域定义为风险度量值小于一个给定值的那些风险所组成的集合,则对于具有平移不变性的风险度量ρ,可接受域的定义如下:
对于VaRτ,风险Yi的可接受域Aρ可以表示为[13]:
对于期望分位数EVaRτ,风险Yi的可接受域可以表示为:
由此可见,在应用VaRτ风险度量的条件下,如果损失小于特定额度的概率与损失大于特定额度的概率之比足够大,那么这个风险就是可接受的。在应用期望分位数EVaRτ的条件下,如果特定额度以下损失的期望值与特定额度以上损失的期望值之比足够大,那么这个风险就是可以接受的。
在期望分位回归中,假设因变量Yi在τ水平下的期望分位数Q(τ|xi)与协变量xi有如下的关系:
其中,φ(τ)表示在τ分位数水平下的回归系数。
通过最小化下述的非对称平方损失函数可以求得期望分位回归的系数φ(τ):
当分位数水平τ=0.5 时,分位回归的预测值就是中位数,而期望分位回归的预测值就是均值。
3 两阶段Expectile回归计算风险保费
为了预测每份保单的风险保费,本文应用两阶段建模。第一阶段使用Logistic 回归建立出险概率的预测模型;第二阶段在损失已经发生的条件下,建立累积损失的预测模型。累积损失是保单在整个保险期间的损失金额之和,可以使用Gamma 回归、分位回归、函数系数分位回归或期望分位回归建立预测模型。
3.1 第一阶段建模
令第i份保单未出险的概率为pi=FNi(0|xi),出险概率为1-pi=1-FNi(0|xi),其中,Ni代表第i份保单的索赔次数,FNi代表Ni的分布函数。当第i份保单的风险暴露为ei时,建立Logistic回归模型为:
其中,xi表示协变量,θ为回归系数向量。
3.2 第二阶段建模
令Yi代表保单的累积损失(部分保单没有出险,所以他们的累积损失为零),用表示在出险条件下的累积损失(即大于零的累积损失观察值),则:
其中,xi表示协变量,ξ为回归系数向量。
因此,在期望值保费原理和标准差保费原理下,第i份保单的风险保费可以分别表示为:
其中,α表示风险附加系数,伽马回归的离散参数φ为:
其中,I表示有索赔的个体保单数量,r+1 表示模型中回归系数的个数,μi根据Gamma 回归的系数估计值计算得到。
在期望值原理和标准差原理的风险保费计算公式中,令每份保单的风险保费之和等于保单组合的总风险保费,即=C,即可求得相应的风险附加系数α。这里的C表示保单组合的总风险保费。
类比式(16)和基于两阶段分位回归的保费定价原理[2],在第二阶段建模中建立关于非零累积损失的期望分位回归,并提出两阶段期望分位回归,即基于Logistic回归和期望分位回归的结果计算第i个保单的风险保费:
根据式(22)中给定保单组合的总风险保费C,可以计算出使式(22)成立的分位数水平τ,从而求得第i个保单的风险保费。基于两阶段期望分位回归计算风险保费不仅解决了将保单组合的总风险保费C分摊到每一份个体保单的问题,而且避免了在含零累积损失数据中对非零累积损失数据建模需要借助索赔概率pi转化分位数水平的问题[1,6],简化了计算过程。如果第二阶段建立的是关于的分位回归或函数系数分位回归,那么可以将替换为分位回归或函数系数分位回归的预测值。利用式(22)求得使等式成立的分位数水平τ,得到分位回归和函数系数分位回归模型下的风险保费分别为和。
4 实例
在风险保费定价模型的有关研究中,R 程序包insuranceData 中的dataCar 数据集被多次用来检验和比较不同模型的预测性能[1,14,15],该数据集包含67856份保单的损失观察值。为了与现有文献中的模型进行比较,本文也选用该数据集进行建模,有关变量的名称和含义如下页表1所示。
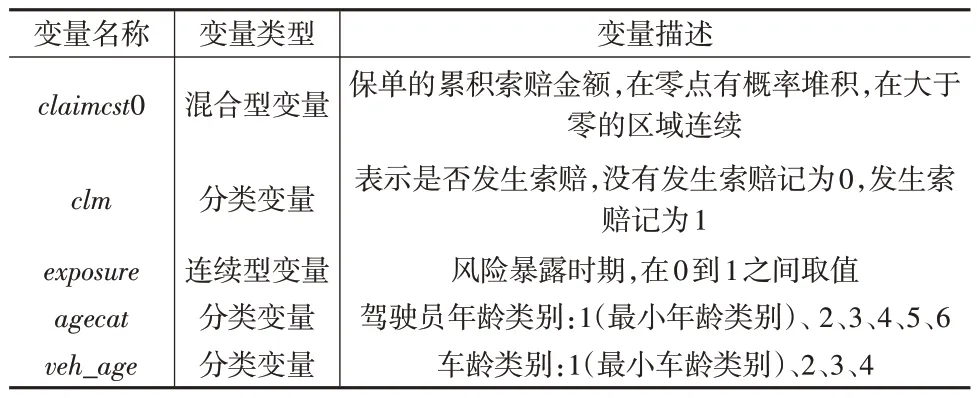
表1 数据集dataCar的有关变量
保单的累积索赔金额存在明显的厚尾性,索赔金额经过对数变换以后的分布如下页图1所示,本文使用经过对数变换以后的索赔金额作为因变量进行回归建模。
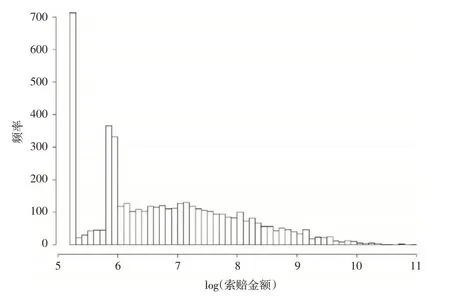
图1 索赔金额对数的直方图
驾驶员年龄agecat有6 个水平,车龄νeh_age有4 个水平,他们的不同组合形成了24 个风险类别,如下页表2所示。其中,V是车龄νeh_age,A是驾驶人年龄,例如V=1,A=1 代表νeh_age=1 且agecat=1。表2 也列示了每个类别的保单数、风险暴露、发生索赔的保单数、索赔次数,以及发生索赔保单的平均索赔金额。
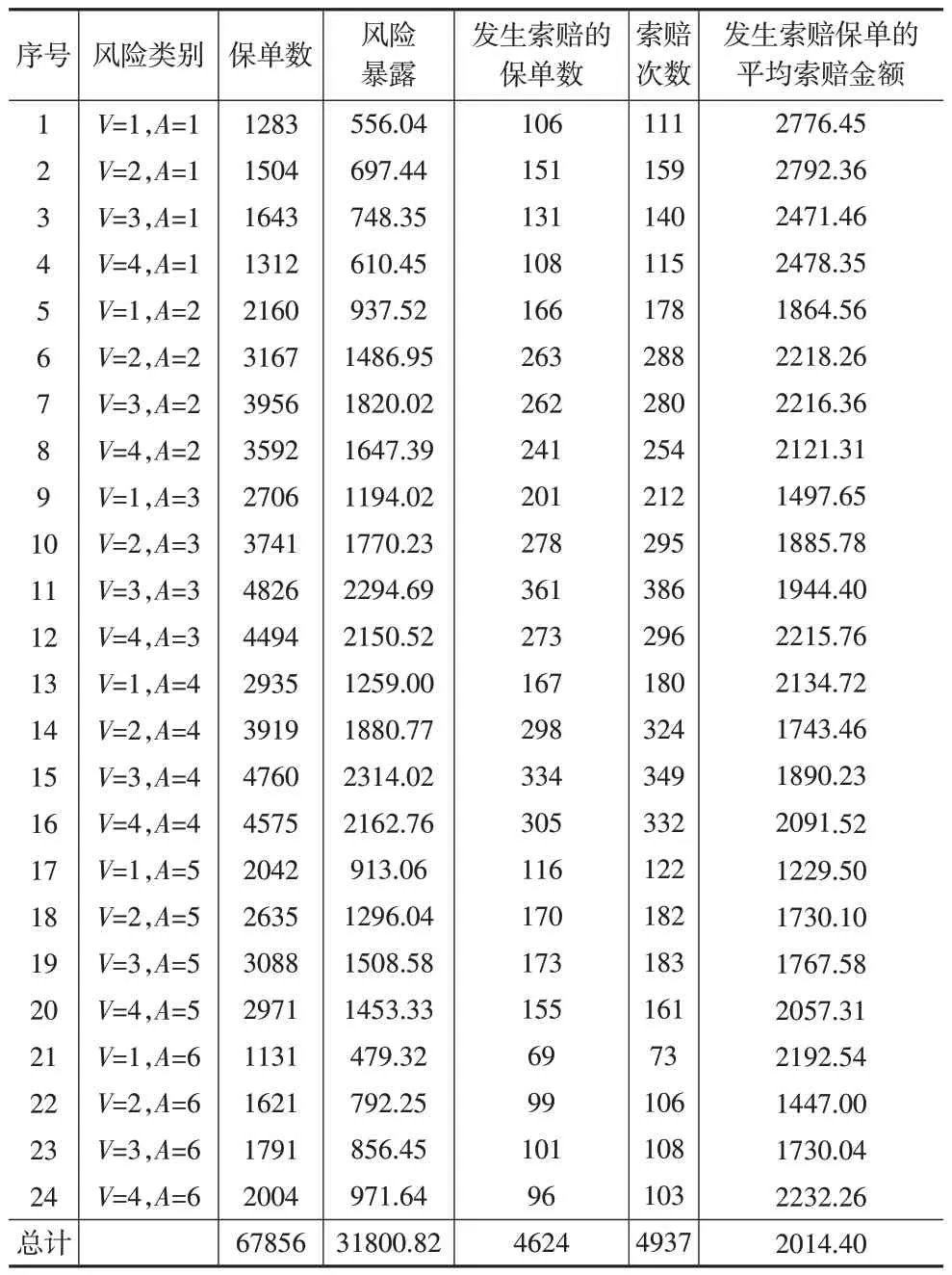
表2 各个风险类别的数据特征
本文采用自上而下的方法厘定各个风险类别的风险保费,先根据保单组合的历史索赔数据,计算保单组合的总风险保费,使得总风险保费大于实际索赔金额的概率足够大,比如达到99.9%;再应用回归模型计算各个风险类别的风险保费,并要求保单组合的总风险保费等于各个风险类别的风险保费之和,在这种约束条件下可以求得唯一的风险附加系数或分位数水平。
在本例中,将总索赔金额的99.9%分位数作为保单组合的总风险保费C,即可确保该保单组合的实际索赔金额大于总风险保费的概率不超过0.1%,即保险公司遭受亏损风险的概率不超过0.1%。在实际情况中,保险公司可以根据自身情况调整分位数水平,本文以99.9%的分位数水平为例进行展示。为了计算保单组合的总风险保费,可以利用Bootstrap 方法从67856 份保单中有放回地随机抽取67856个样本计算总索赔金额,一共抽取10000次,得到10000个总索赔金额的随机样本,由此可以较好地逼近总索赔金额的真实分布(当样本足够大时,Bootstrap 方法能够无偏地接近总体分布,估计结果精度高且稳定[16])。如果将总索赔金额的99.9%分位数作为保单组合的总风险保费,那么总风险保费为C=10192385。下面计算每个风险类别的风险保费,使其总和正好等于保单组合的总风险保费。
下页表3 展示了Logistic 回归、Gamma 回归、分位回归、函数系数分位回归、期望分位回归的系数估计值以及相应的标准误和P值。在分位回归、函数系数分位回归和期望分位回归模型中,应用式(22),可以求得相应的分位数水平分别为75.41%、74.33%和84.97%。从表3 可以看出,各个模型的回归系数估计值在正负号上基本一致,车龄(V)越大,索赔概率越低,索赔金额越大;驾驶人年龄(A)越大,索赔概率越低,索赔金额越小。
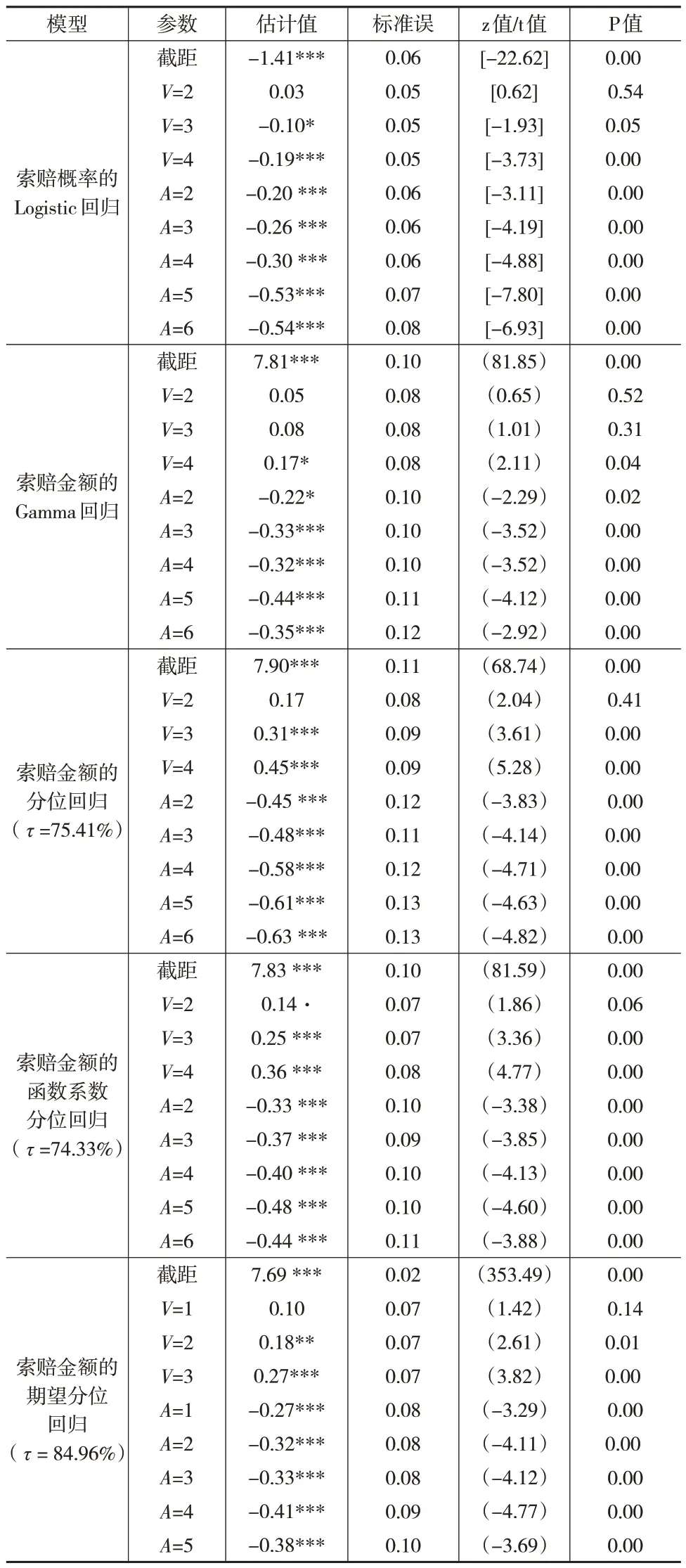
表3 回归模型的参数估计值
下页表4 展示了应用Logistic 回归预测的各风险类别的索赔概率、基于Gamma 回归预测的各风险类别的纯保费,以及应用不同方法计算的风险保费。本例中,如果要求各个风险类别的风险保费之和等于总风险保费,那么在期望值原理和标准差原理下,求得的风险附加系数分别为α=10.06%和α=1.94%。
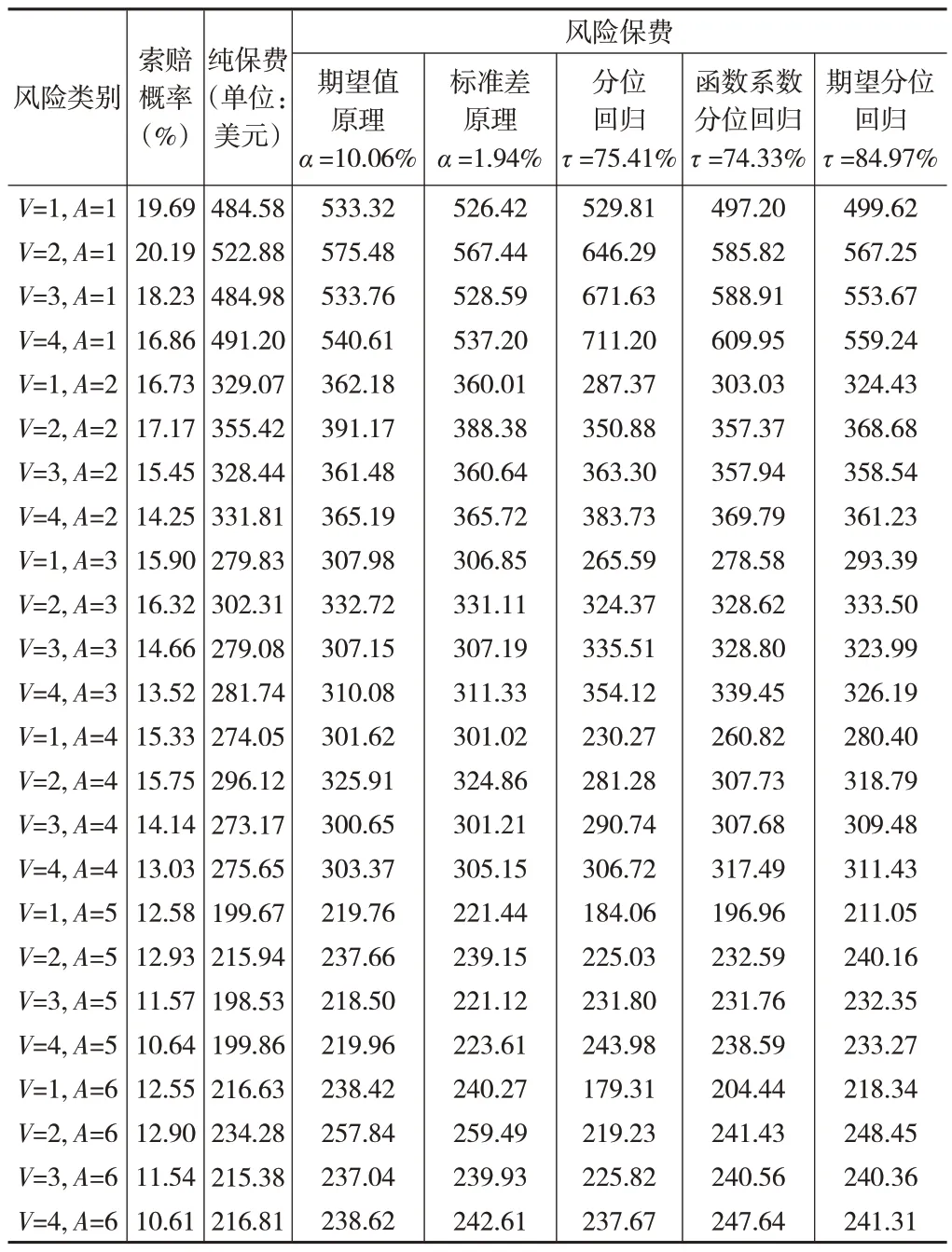
表4 不同方法计算的风险保费
前面应用五种模型求得了五种不同的风险保费,为了比较他们的相对优劣,每次将其中一个模型作为基准模型,其他模型作为竞争模型,计算竞争模型的风险保费与基准模型的风险保费之比Ri(i=1,2,…,I),根据Ri从小到大的顺序对基准模型的风险保费和实际损失观察值进行排序,并据此绘制有序洛伦兹曲线,计算基尼指数,结果如下页表5 所示。基尼指数的具体计算方法参见文献[17]。
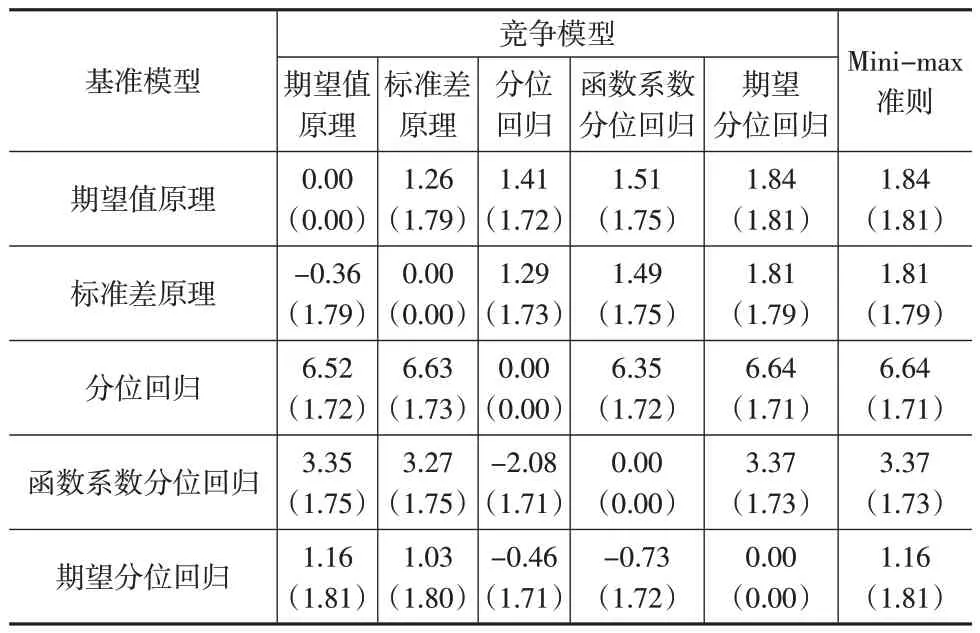
表5 基于基尼系数的模型比较(单位:%)
从表5 可以看出,若以期望值原理作为基准模型,则它的相对最大劣势为1.84;若以标准差原理为基准模型,则它的相对最大劣势为1.81。类似地,分别以分位回归、函数系数分位回归和期望分位回归作为基准模型时,他们各自的相对最大劣势分别为6.64、3.37 和1.16。根据Mini-max 准则,期望分位回归作为基准模型时的相对最大劣势只有1.16,数值最小,所以它在上述五个模型中是最优模型。
应用期望分位回归厘定的风险保费具有良好的可解释性。下页图2 是期望分位回归与Gamma 回归的系数估计值在分位数水平τ∈[0,1]上的情况。实线表示期望分位回归的系数估计值,阴影部分表示其置信水平为95%的置信区间,虚线表示Gamma 回归系数估计值。Gamma 回归与期望分位回归的系数估计值正负号在大部分分位数水平上保持一致,且每幅图在τ∈[0.8,1]上均有交集。截距项代表的是基准类别V=1,A=1的系数估计值。分位数水平τ升高,截距项的估计值随之上升,说明保险公司需要收取更高的风险保费来平衡V=1,A=1不断增长的风险水平。期望分位回归的系数估计值代表了不同类别之间风险保费的相对差异。例如,图2(b)展示了类别V=2,A=1 与V=1,A=1 在风险保费上的相对差异。当系数估计值大于0时,两个类别的风险保费之比大于1,说明V=2,A=1 的风险保费比V=1,A=1 高,前者的相对风险水平更高;小于0 则反之。根据图2(b)可知,期望分位回归的系数估计值起初随着τ的增大而增大,且为正值,说明V=2,A=1 的风险保费更高。当τ→1 时,系数估计值迅速下降并且变为负值。因此,在极端分位数水平上,V=2,A=1 的风险保费下降,最终小于类别V=1,A=1 的风险保费。从图2 还可以看出,车龄(V)的回归系数大多数情况下大于零,说明随着汽车使用年限的增大,风险保费逐步提高;驾驶人年龄(A)的回归系数在大多数情况下小于零,说明随着驾驶人年龄的增大,风险保费越来越低。
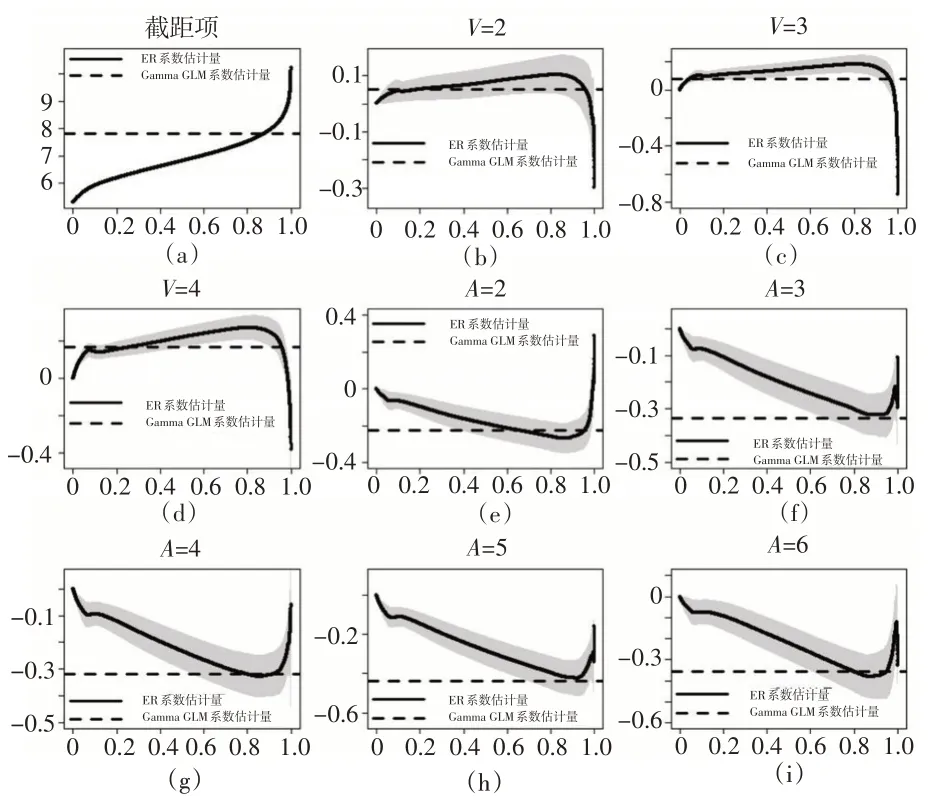
图2 分位数水平对期望分位回归系数的影响
5 结论
在风险保费的理论与应用研究中,关于纯保费的研究较多,而对风险附加的关注相对较少。期望分位数的理论性质表明,应用期望分位数预测风险保费具有一定优势,可以更好地满足保险定价的实际需要。本文提出期望分位数保费原理,即应用期望分位回归预测风险保费,代替基于广义线性模型的期望值保费原理和标准差保费原理以及基于分位回归的分位数保费原理。对非零损失数据使用期望分位回归建模,令各个风险类别的分位数水平一致,避免了需要借助水平概率转化分位数水平的问题,简化了计算过程。此外,为了基于实际数据确定各种保费原理中的风险附加系数或分位数水平,本文提出了一种自上而下计算风险保费的方法,避免了现有文献中确定风险附加系数和分位数水平的主观任意性。基于R程序包insuranceData 中一个实际数据集dataCar 进行的实证分析结果表明,应用期望分位回归预测风险保费要优于现有方法。
为了与现有文献中的其他模型在相同基础上进行比较,本文在建立期望分位回归模型时,仅考虑了现有文献中使用的变量,并没有考虑变量之间的交互效应和非线性效应。此外,在后续研究中,可以尝试将函数系数引入期望分位回归,建立参数系数的期望分位回归模型,进一步提高期望分位回归模型在风险保费厘定中的灵活性。
