自然环境中混凝土内微环境温度响应*

刘 鹏,余志武†, 宋 力,陈令坤

(1. 中南大学 土木工程学院,湖南 长沙 410075；2. 中南大学 高速铁路建造技术国家工程实验室,湖南 长沙 410075)

混凝土结构工程的耐久性和使用寿命等受自然环境温度影响显著,国内外学者对此进行了大量研究并取得了丰硕的成果[1-3].自然环境中的混凝土结构工程,其所受的温度影响应指混凝土内微观环境温度而非自然环境温度[4]；然而,既有研究成果为了简化起见,均将自然环境温度直接等效为混凝土内微环境温度,这显然与自然环境中混凝土结构实际情况不符,故采用简单地代换所建立的模型隐含较大潜在误差且难以预控,由此预测和评估出的混凝土结构工程的使用寿命偏差较大.与此同时,研究还表明,混凝土结构工程所处位置与吸收太阳辐射的热量密切相关,进而造成的温度响应亦有差异[5-6].鉴于此,混凝土结构工程性能评估过程中要充分考虑其所处环境和所处位置的双重影响.若将自然环境温度对混凝土的影响视作一种荷载(作用力)予以考虑,通过建立两者间的相关性则可用于表征其对混凝土的影响；然而,鉴于自然环境温度变化的复杂性和不确定性使得关于自然环境温度与混凝土结构所处位置间的相关性研究较少.若采用直接根据实测资料拟合温度间的相关性的方法,则拟合函数受主观因素影响较大且拟合精度还受到观测点数目及其观测精度的限制，这使得该法难以推广到缺乏观测数据的工程中[7-8].因此，有必要对有/无遮挡条件下自然环境温度与混凝土内温度响应规律进行探讨.

本文基于Fourier导热原理、欧拉方程和第三类边界条件,推导出了有/无遮挡条件下自然环境中混凝土内微环境温度响应模型,并利用实测数据验证了该模型的正确性.此外,本文还试探出了求解混凝土热扩散系数等参数的方法.通过构筑基于有/无遮挡条件下自然环境温度变化的混凝土内微观环境温度响应谱模型,为下一步的人工室内模拟试验的温度参数的设定提供了理论依据.

1 理论推导

1.1 混凝土内温度响应模型

对于热扩散系数受温度等因素影响较小的物质,其非稳态导热过程可用Fourier导热方程表示[9-11]：

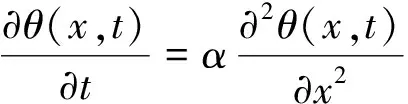
(1)

式中θ(x,t)为t时刻混凝土内深度为x的温度值,℃；t为时间,s；x为测试点距混凝土表面深度,m；α为热扩散系数, m2/s.

假定混凝土表面的温度是一个已知的时间函数θ(t),它是一个周期为2π/ω(ω为角频率)的函数；设θ(x,t)代表在时刻t混凝土内深度为x处的温度.对其展开为傅立叶级数的复数形式,如式(2)和(3)所示：

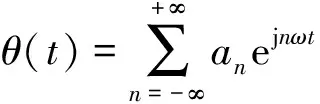
(2)

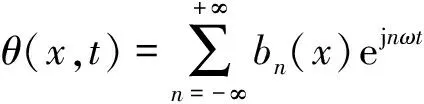
(3)

傅立叶系数bn(x)是深度x的函数.假定混凝土外表层温度bn(0)=an,而内部一定深度处的温度波动可忽略,则混凝土内的温度波动方程可由式(1)和(3)求得：

(4)

假设式(4)的试探解为幂指数形式：

bn(x)=an·eSx

(5)

则由式(4)和(5)得：

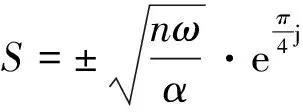
(6)

则式(5)可表示为：

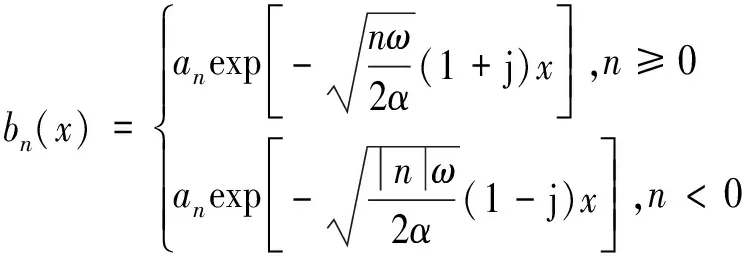
(7)

大量资料和研究表明,自然环境温度周期性变化可看作简谐波,则混凝土表层温度亦可用余弦(或正弦)函数形式表示[12],如式(8)所示：

θt=θa+θ0cos(ωt-φ)

(8)

式中θt为t时刻混凝土表层温度,℃；θa为温度波的平均值,℃;θ0为温度变化幅值,℃;ω=2π/T为角频率,rad/s;T为温度波动周期,h;t为相应时间,h;φ为相位角,rad.若令τ=t-φ/ω,则 式(8)可转化为式(9).

θτ=θa+θ0cos(ωτ)

(9)

式(9)所对应的傅立叶级数复数形式的系数分别为：

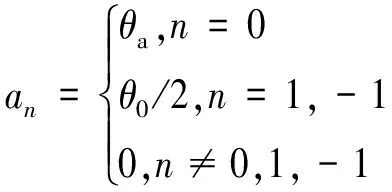
(10)

则由式(7)可得相应的系数为：

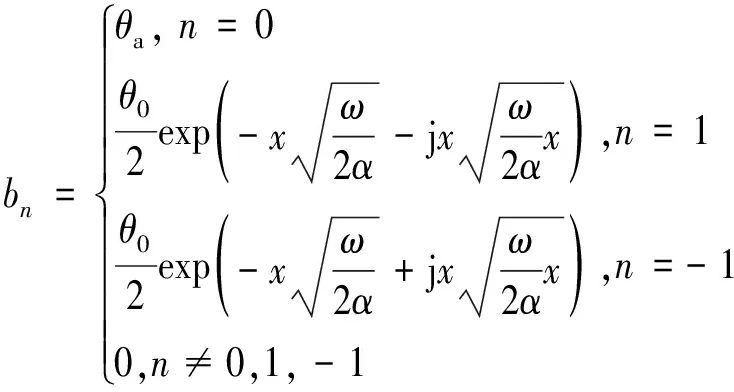
(11)

利用欧拉公式整理式(3)和(11)并求解,可得：

(12)

将τ=t-φ/ω代入式(12),可得：

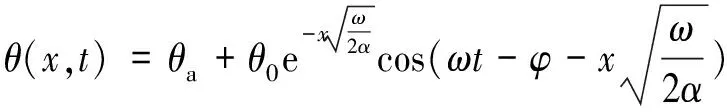
(13)

式(13)即为基于傅立叶导热原理和欧拉方程的一维混凝土内温度响应模型.分析式(13)中温度响应模型的幅值衰减和相位(时间)滞后可知,在混凝土的热扩散系数α(导温系数)未知的情况下,可通过测定混凝土内不同深度处温度幅值或相位滞后大小来求解α值.假设一维混凝土内的不同深度处x1和x2,其相应的幅值衰减和相位滞后可用式(14)(15)表示：

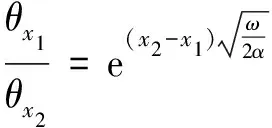
(14)

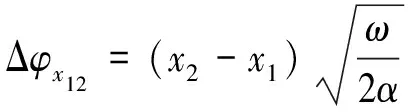
(15)

则热扩散系数α可表示为：

(16)

式(16)即为幅值和相位法求解混凝土热扩散系数方程.若条件不够充分,亦可通过测定混凝土内同一深度不同时刻的温度值,来间接求出其热扩散系数，这对于求解不同深度处因含水率、孔隙率和微观结构差别较大而导致热扩散系数明显不同的情况提供了新途径,其相应的公式可简称为时差法,如式(17)所示：

(17)

式中θ(x,t)为t时刻混凝土内深度x处的温度,℃；x为混凝土内深度,m;θ0为自然环境温度作用谱幅值,℃；φ为自然环境温度作用谱相位角,rad；α为热扩散系数,m2/s;ω为自然环境温度波动角频率, rad/s.

1.2 有遮挡条件下的混凝土内温度响应与自然环境温度间的相关性

有遮挡条件下的混凝土工程(如工程背阴面和被遮挡等)与自然环境间传热方式主要为对流换热(直接和散射辐射换热等可忽略),相应的导热方程为第三类边界条件——假定经过混凝土表面的热流量与混凝土表面温度和外界气温之差成正比,可用式(18)表示[13-14]：

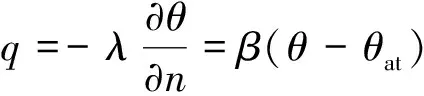
(18)

式中θ为混凝土表面温度,K；θat为自然环境气温, K；λ为混凝土导热系数,W/(m·K)；β为混凝土表面与空气间表面换热系数,W/(m2·K)；n为表面外法线方向；q为热流量,W/m2.

式(13)对混凝土内深度x求导,可得混凝土内温度梯度, 见式(19)：

(19)

联立方程式(13)，(18)和(19),可求得混凝土表层附近的空气温度：

θat(t)=θa+

(20)

式(20)即为基于有遮挡条件下的混凝土表层温度和自然环境温度间的相关性模型.

1.3 无遮挡条件下的混凝土内温度响应与自然环境温度间的相关性

众所周知,大多数混凝土结构直接暴露于自然环境的太阳照射下,其与外界间热量交换主要依靠对流换热和辐射,故混凝土内温度响应模型有别于有遮挡或背阴条件下混凝土内温度响应模型.混凝土在太阳辐射的作用下,考虑日照的导热边界条件可用式(21)表示：

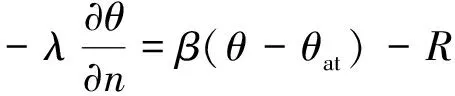
或

(21)

R=aQ

(22)

式中R为太阳辐射热量被吸收部分,W/m2；Q为相应的太阳总辐射热量,W/m2；a为吸收系数或黑度系数[13],对于混凝土可取0.65；其余符号同上.

计算太阳总辐射热量最为典型的为半正弦模型和Collares-Pereira & Rabl模型[15-16]. Collares-Pereira&Rabl模型:

Q(t)=Qa(I0/Q0)(a+bcosωt)

(23)

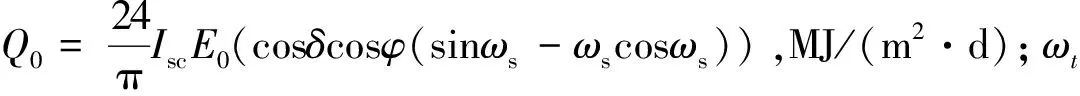
半正弦模型：

(24)

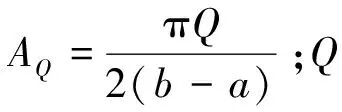
联立方程式(13)，(21)，(22)和(23)可知,当获取现场地理和太阳日总辐射量等信息后,即可建立无遮挡条件下混凝土内温度响应模型与自然环境温度作用模型间的联系,如式(25)所示：

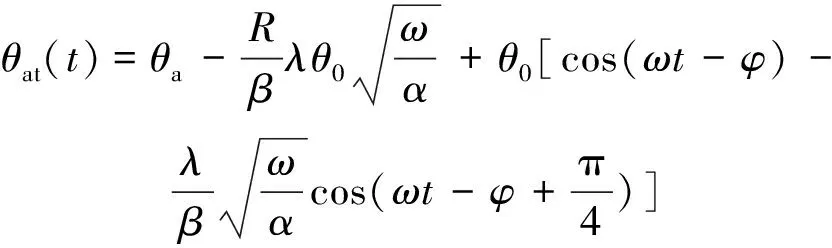
(25)

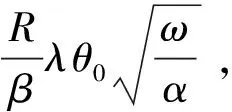
从式(21)还可看出,若无辐射传热(即R=0)则其转化为式(18)．这表明若利用所求解的混凝土热扩散系数α值(式(16)和(17))、混凝土表面温度梯度(即式(19))和温度(即式(8))及其自然环境温度等参数,则可推导出混凝土与自然环境间的实时表面换热系数β值.该法克服了传统求解表面换热系数的不足(如多基于稳态传导,试样与现场实况误差大等),能用于实时求解自然环境与混凝土间的表面换热系数,这为研究现场自然环境和人工模拟环境提供了理论依据.此外,从上述推导亦可知,若利用式(16)，(19)，(21)和(22)及其测定的混凝土与自然环境温度等参数,则可反推导出太阳实时总辐射热量,这为获取现场实时太阳总辐射热量提供了求解方法.

2 试 验

2.1 试验原料、混凝土配制及试验仪器

试验所用的主要原料为P·O 42.5级硅酸盐水泥(湖南长沙平塘水泥厂),聚羧酸系列高效减水剂(湖南长沙黄腾外加剂厂),I级粉煤灰(湖南湘潭电厂),S95级矿粉(湖南涟源钢铁集团有限公司产),长沙本地产河砂(细度模数约为2.9),连续级配粒径5 ～20 mm石灰岩碎石,长沙本地自来水.配制C30级混凝土所用原料配比(质量比)为水泥∶矿粉∶粉煤灰∶砂∶石∶水∶减水剂为290∶50∶60∶730∶1 050∶164∶4.2.所采用的温度测定仪为湖南省长沙市三智电子科技有限公司生产的SHT10温湿度传感器,测试前应对其精度进行校正,其精度为±0.1 ℃,扫描响应时间为5 s,漂移量小于0.4 ℃/yr,可实时测定温度值.

2.2 试样制作与试验过程

按照JTG E 30—2005《公路工程水泥及水泥混凝土试验规程》和T0553—2005《水泥混凝土立方体抗压强度试验方法》的力学性能试验要求安排实验；浇筑尺寸为150 mm×150 mm×150 mm立方体试样,成型24 h后脱模,放入标准养护池中养护；28 d的实测抗压强度约为34 MPa.采用钻芯机从试样侧面取芯,制成直径为100 mm±1 mm,高度为150 mm ±1 mm的圆柱体；然后,利用钻机钻取距表面不同厚度(35 mm和50 mm)的孔,相应孔径约为10 mm ±1 mm, 将温度传感器置入孔中并用相同级配的混凝土砂浆密封；养护一定程度后,将所制备的含传感器的试样置于杜瓦瓶中(其端面与杜瓦瓶口平齐),并采用相同级配的混凝土浇筑成型和养护；根据测试要求,将试样长时间(不少于3个月)置于所测自然环境中,以使得混凝土内各处温湿度基本一致.图1为用于测定一维混凝土内温度响应规律的试件简图.

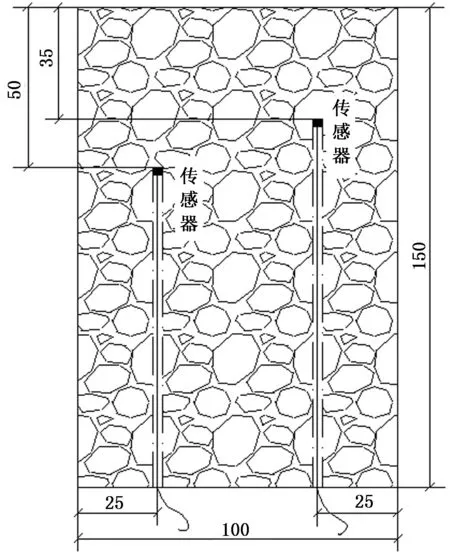
图1 混凝土温度响应试样(mm)

图2为相应的实物图.测试有遮挡条件下混凝土内温度响应规律的过程中,将试样置于四周空旷且距地高度约为1.5 m的百叶箱中,传感器一端连接测定仪,记录不同时刻环境温度值和混凝土内不同深度温度响应值;自然环境温度随时间变化规律亦采用温度传感器测定,其探头直接悬挂于百叶箱中间;与之相比,无遮挡条件下混凝土内温度响应规律测定过程中,试样置于相同场地距地高度约为1.5 m钢筋架上.

图2 混凝土温度响应试件实物

3 分析与讨论

3.1 有遮挡条件下自然环境中混凝土内温度响应

为了更好地研究自然环境温度和混凝土内温度变化规律,本文以长沙地区2011年8月16至18日为例研究了有遮挡条件下自然环境中的混凝土内不同深度处温度的变化特征,并对17日的实测结果进行了拟合,相应的测试结果及其部分拟合曲线如图3所示.

时间/h

从图3可以看出,自然环境温度和混凝土内温度呈现出有规律的周期性变化,其波动周期约为24 h,利用所建立的正弦(余弦)函数模型拟合实测结果可大致描述温度波动规律.这表明上述所推导理论模型是合理的.至于部分区域出现拟合曲线与实测结果偏离是因昼夜时间长短不等使得升温和降温波动周期不相等造成的,将另文详细阐释.自然环境温度与混凝土内温度间的差别主要表现为混凝土内温度响应波动曲线相对光滑、数据离散性小、温度波动滞后和幅值衰减等方面,这是因混凝土的热传导系数、密度及其比热容等赋予混凝土较大的热阻——起延滞和消弱作用造成的.从图3可知,有遮挡条件下混凝土内温度响应主要受环境变化、混凝土传热系数和表面换热系数影响.利用实测数据的温度波动幅值,结合式(16)可求出混凝土内的热扩散系数约为3 ×10-3m2/h；实测混凝土的密度约为2 300 kg/m3,若取其比热容为920 J/(kg·K),利用实测数据和式(18),则可求得实测现场混凝土表面与空气间的表面换热系数(对流换热)约为20.5 W/(m2·K)；将计算参数代入本文建立的混凝土内温度响应模型,可求出35 mm和50 mm处的相位滞后分别约为0.44和0.54,其与图3中的拟合曲线的相位差基本吻合,这表明该模型具有较好的精度.

3.2 无遮挡条件下自然环境中混凝土内温度响应

大多数混凝土结构工程多暴露于太阳直接照射下,为了研究有/无遮挡对自然环境温度和混凝土内温度变化规律,本文以长沙地区2011年8月19日为例研究了无遮挡条件下自然环境与混凝土内不同深度处温度的变化特征.长沙地区测量现场约处于北纬28.2°,日出时间约为6时,日落时间约为19时,8月19日天气状况与16～18日基本相同,相应的日辐射小时最大值约为1.73 MJ/(m2·h)．鉴于此,该处仅对太阳照射期间(即6～19时)温度变化规律进行探讨,相应的实测温度值及其拟合曲线如图4所示.

时间/h

从图4中可以看出,被太阳直接照射的混凝土内温度响应规律明显有别于有遮挡条件下混凝土内温度响应,主要表现在温度响应的波动幅值增加、温度变化率大、最高温度值增加及其时间提前等方面.本试验所拟合的曲线是基于太阳照射期间温度值,从图4中可以看出分别基于混凝土内温度响应和自然环境温度所推导出的等效环境温度理论拟合基本一致,部分区域略有差异是因参数取值等造成的,这表明上述理论推导所提出的环境等效温度可以用于描述相应日照条件下混凝土内温度响应规律.混凝土内温度随太阳升起而快速增高,随日落急速降低,于13时左右混凝土内(35 mm)的温度出现极大值；而自然环境温度于14.5时左右达到最大值,其随日落而缓慢降低；无太阳照射期间混凝土内温度响应规律与有遮挡条件下的响应规律相似.无遮挡条件下,混凝土获得的热量主要来源于太阳辐射能量——部分辐射能转化为混凝土内能以提高自身温度,另一部分以红外线形式散射入环境中.混凝土温度极大值是在其接受太阳辐射能和自身散射失掉的能量达到平衡后出现的——若混凝土获取的辐射能量大于散射失掉能量,则多余的能量将转化为混凝土内能以升高混凝土温度；若散失能量大于混凝土通过辐射获取的能量,则混凝土温度会逐渐降低；故混凝土表层温度达到最大值会出现在混凝土获取的辐射能与散失掉的能量达到平衡时刻.环境温度升高主要是通过吸收混凝土散射能量(红外线)而到达的,混凝土向大气散失能量需要一个时间过程,此即为相应的滞后时间.因而,自然环境温度出现极大值滞后于无遮挡条件下混凝土出现温度极大值时刻.产生这两者差异是由于有/无遮挡条件下混凝土与外界环境之间热能传输方式不同造成的.在有遮挡条件下,混凝土与环境间传热主要以表面对流换热为主；而太阳照射条件下,两者间换热方式由辐射和对流换热主导.辐射至混凝土表面的热能大量传导入混凝土内,从而使得混凝土温度快速升高,部分能量以对流换热和辐射方式传递给空气.从图4中还可以看出,太阳照射的混凝土内温度响应值远远大于自然环境温度,理论计算混凝土表层温度可超过50 ℃,这表明混凝土内温度响应规律受其获取能量的方式影响显著,自然环境温度变化规律能否直接等效于混凝土内温度变化规律,应视混凝土所处自然环境条件而定，这为人工室内模拟试验温度参数选取提供了依据.

4 结 论

1)基于傅立叶导热方程和欧拉公式推导出了自然环境中有/无遮挡条件下的混凝土内微观环境的温度响应模型,实测结果表明，两者之间差异显著.无遮挡条件下混凝土内温度响应规律主要表现为温度响应更敏感、波幅较大和极值出现时间提前等方面；而有遮挡条件下混凝土内温度响应却出现滞后与衰减.这两者间的差异是因主导混凝土与自然环境间换热方式不同造成的.

2)利用现场试验温度响应求解混凝土内热扩散系数和表面换热系数等参数是可行的,且可将太阳辐射传热效果等效为环境温度作用.所求混凝土相应的热扩散系数约为3×10-3m2/h,其表面换热系数约为20.5 W/(m2·K).

3)实测结果和理论分析表明，混凝土内温度响应规律受其获取能量的方式影响显著,自然环境温度变化规律能否直接等效于混凝土内温度变化规律,应视混凝土所处自然环境条件而定.

[1]YUAN W, SEFIANE K. Effects of heat flux, vapour quality, channel hydraulic diameter on flow boiling heat transfer in variable aspect ratio micro-channels using transparent heating [J]. International Journal of Heat and Mass Transfer, 2012, 55(9):2235-2243.

[2]SCHINDLER A K, RUIZ J M, RASMUSSEN R O,etal. Concrete pavement temperature prediction and case studies with the FHWA HIPERPAV models [J]. Cement and Concrete Composites, 2004, 26(5): 463-471.

[3]范宏, 王鹏刚, 赵铁军.长期暴露混凝土结构中的氯离子侵入研究[J].建筑结构学报, 2011, 32(1):88-95.

FAN Hong, WANG Peng-gang, ZHAO Tie-jun. Research on chloride penetration for RC structures after long-term exposure[J]. Journal of Building Structure, 2011, 32(1): 88-95.(In Chinese)

[4]蒋建华, 袁迎曙, 张习美. 自然气候环境的温度作用谱和混凝土内温度响应预计[J]. 中南大学学报, 2010,41(5): 1923-1930.

JIANG Jian-hua, YUAN Ying-shu, ZHANG Xi-mei. Action spectrum of temperature in natural climate environment and prediction of temperature response in concrete[J]. Journal of Central South University, 2010, 41(5): 1923-1930. (In Chinese)

[5]李志磊, 干钢, 唐锦春. 考虑辐射换热的建筑结构温度场的数值模拟[J]. 浙江大学学报,2004, 38(7):915-919.

LI Zhi-lei, GAN Gang, TANG Jin-chun. Numerical simulation of temperature field of building structures considering radiation[J]. Journal of Zhejiang University, 2004, 38(7):915-919. (In Chinese)

[6]JONES G F, JONES R W. Steady-state heat transfer in an insulated, reinforced concrete wall: theory, numerical simulations, and experiments [J]. Energy and Buildings, 1999, 29(3):293-305.

[7]曹为民, 吴健, 闪黎. 水闸闸墩温度场及应力场仿真分析[J]. 河海大学学报,2002, 30(5):48-52.

CAO Wei-min, WU Jian, SHAN Li. Numerical simulation of temperature field and stress field of sluice piers[J]. Journal of Hohai University, 2002, 30(5):48-52. (In Chinese)

[8]YOUSEF S, ALNASSAR M, NAOOM B,etal. Heat effect on the shielding and strength properties of some local concretes [J]. Progress in Nuclear Energy, 2008, 50(1): 22-26.

[9]INCROPERA F P, DEWITT D P, BERGMAN T L, 等.传热和传质基本原理 [M].葛新石, 叶宏,译.北京:化学工业出版社,2009:30-50.

INCROPERA F P, DEWITT D P, BERGMAN T L,etal. Fundamentals of heat and mass transfer[M]. Translated by GE Xin-shi, YE Hong. Beijing: Chemical Industry Press, 2009:30-50. (In Chinese)

[10]REMIE M J, SARNER G, CREMERS M F,etal. Heat-transfer distribution for an impinging laminar flame jet to a flat plate [J]. International Journal of Heat and Mass Transfer, 2008, 51(11): 3144-3152.

[11]王补宣.工程传热传质学[M].北京:科学出版社,2002:52-60.

WANG Bu-xuan. Heat and mass transfer of engineering [M]. Beijing: Science Press, 2002:52-60. (In Chinese)

[12]TEMEEMI A A, HARRIS D J. The generation of subsurface temperature profiles for Kuwait [J]. Energy and Buildings, 2001, 33(8):837-841.

[13]朱伯芳. 大体积混凝土温度应力与温度控制[M]. 北京:中国电力出版社,1998:10-13.

ZHU Bo-fang. Thermal stresses and temperature control of mass concrete [M]. Beijing: China Electric Power Press, 1998:10-13. (In Chinese)

[14]汪剑,方志. 混凝土箱梁桥的温度场分析[J].湖南大学学报:自然科学版, 2008,35(4):23-29.

WANG Jian,FANG Zhi. Temperature variation of concrete box girder bridge[J]. Journal of Hunan University: Natural Sciences, 2008, 35(4):23-29. (In Chinese)

[15]张素宁, 田胜元. 太阳辐射逐时模型的建立[J].太阳能学报,1997,18(3):273-276.

ZHANG Su-ning, TIAN Sheng-yuan. The institution of the hourly solar radiation model[J]. Acta Energiae Solaris Sinica, 1997,18(3):273-276. (In Chinese)

[16]COLLARES M, RABL A. The average distribution of solar radiation correlations between diffuse and hemispherical and between daily and hourly insolation values [J]. Solar Energy, 1979, 22(2):154-164.