在再生核空间中带有积分边值条件的分数阶偏微分方程的近似解
2014-09-17王文佳
王文佳
(哈尔滨师范大学)
0 引言
分数阶偏微分方程正在广泛应用于流体流动、金融、控制论等各种领域[1-4].近年来,更多的努力被投入到寻找分数阶偏微分方程的有效解上[5-7].该文用再生核方法求解一类含有积分边值条件的分数阶偏微分方程.考虑下面的分数阶微分方程:
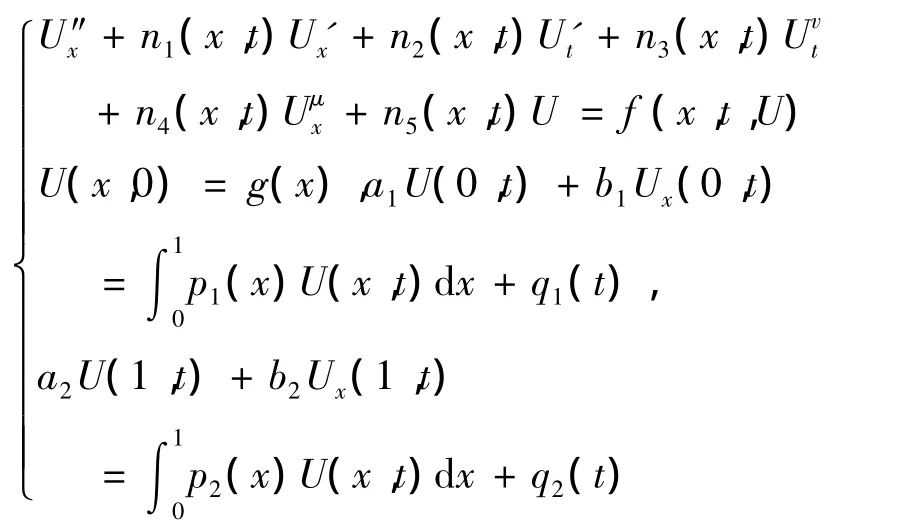
其中ni(x,t),g(x),pj(x),qj(t),i=1,2,3,4,5,j=1,2 是已知函数,ai,bi(i=1,2)是给定的常量.ν∈ (0,1),μ∈ (0,2),x∈ (0,1),t∈ (0,T),U(x,t)是待求函数.以上分数阶微分方程采用Caputo意义下的定义.详见文献[8].
1 再生核空间
u″(x)∈L2[0,T],u(0)=0.其内积为

定义 1.2 定义内积空间W12[0,T] ={u(x)|u(x)}是[0,1]上的绝对连续实值函数,u'(x)∈L2[0,T]}.其内积为:〈u(x),
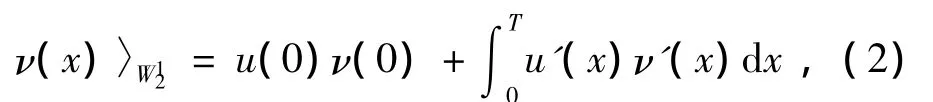
定义 1.3 定义内积空间W32[0,1] ={u(x)|u(x),u'(x),u″(x)是[0,1]上的绝对连续实值函数,u″(x)∈L2[0,1],且aiu(i-1)+

定理1.2 函数空间W32[0,1]是再生核空间.
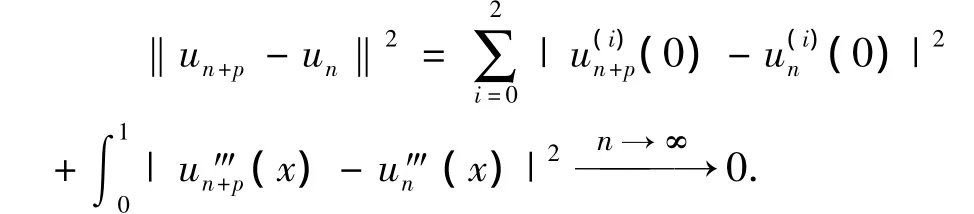

下证其是再生核空间,由文献[9]中定理1.1知只需证对任意的u(x)∈,存在正数Cx,使得|u(x)|≤Cx‖u(x)‖.因为u(x)=,所以|u″(x)|≤|u″(0)|+
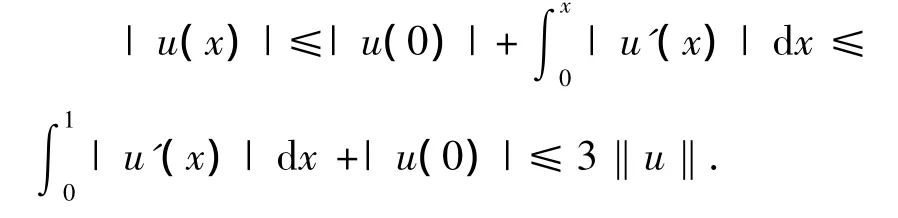
其中m1,m2为待定系数,Ry(x)是的再生核函数,进而Ry(x)满足以下微分方程组:

又由Ry(x)的光滑性得

及边值条件知a1u(0)+b1u'(0)-
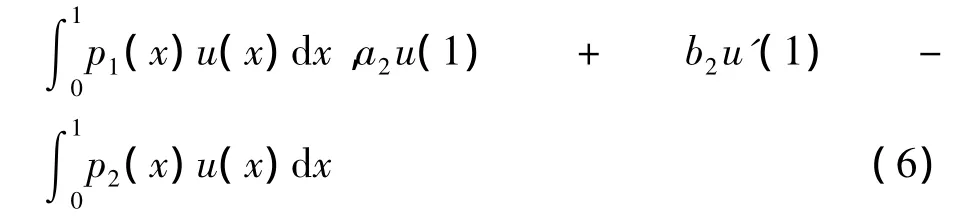
故再生核Ry(x)的一般形式为

其系数由上述(4)-(6)共14个方程唯一确定.
定义1.4 令D=[0,1]×[0,T],定义空间,

2 数值解
在该节中,将以级数的形式给出方程(1)的数值解,为了能够在再生核空间中求解 (1), 引 入 线 性 算 子→
定 理 2.1Ψi(x,t)∈, 且 是的一个完全系.
定理2.2 方程(7)的解可被表达为u(x,t)
定理2.1,2.2 证明参见文献[9].从而方程的近似解为
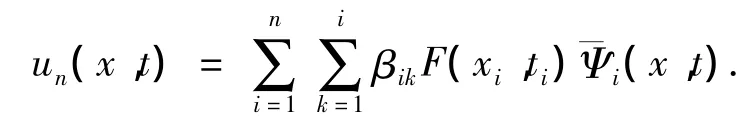
定理2.3 设εn(x,t)是截断误差,则εn(x,t)依范数单调递减.
所以εn(x,t)依范数单调递减.
[1] Meerschaert M M,Benson D,Scheffler H P,et al.Stochastic solution of space-time fractional diffusion equations.Phys Rev,2002,E 65:1103-1106.
[2] Benson D A,Wheatcraft S W,Meerschaert M M.Application of a fractionaladvection-dispersion equation,Water Resour Res,2000,36(6):1403-1412.
[3] Gorenflo R,Mainardi R,Scalas E,et al.Fractional calculus and continuous-time finance.III.The diffusion limit,in:Math Finance,Konstanz,2000,in:Trends Math,Birkhser,Basel,2001.171-180.
[4] Machado J T.Discrete time fractional-order controllers.Frac Calc Appl Anal,2001(4):47-66.
[5] Meerschaert M M,Tadjeran C.Finite difference approximations for two-sided space-fractional partial differential eqations.Appl Numer Math,2006,56:80-90.
[6] Tadjeran C,Meerschaert M M.A second-order accurate numerical method for the two-dimensional fractional diffusion equation.J Comput Phys,2007,220:813-823.
[7] Luchko Y,Srivastava H M.The exact solution of certain differential equations of fractional order by using operational calculus.Comput Math App,1995,29:73-8.
[8] Podlubny I.Fractional Differential Equations.Academic Press,New York,1999.
[9] 吴勃英,林迎珍.应用型再生核空间:第一版.北京:科学出版社,2012.
[10] Cui Minggen,Lin Yingzhen.Nonlinear Numerical Analysis in the ReproducingKernel Space.Nova Science Publisher,New York,2009.
