一类弦振动问题的计算机辅助分析*
2014-09-17孙丽男张馥菊
孙丽男,张馥菊
(1.黑河学院;2.大连理工大学;3.哈尔滨师范大学)
0 引言
弦振动问题是数学物理方程中的经典问题,弦振动理论在生产、生活中有着较为广泛的应用.如对于斜拉桥、高空观光缆车运行安全和游客人身安全而言,检测并控制钢索工作过程中的张力是至关重要的,而此类问题最终归结为弦振动问题的研究.另外,工厂车间进行络纱时,可以观察到纱会以相当快的速度沿着中心轴进行退绕,达到一定条件时便会形成多节气圈,这种现象也可以通过弦振动理论加以说明.弦振动是波动的一种特殊形式,因此弦振动理论在声学中也占有举足轻重的地位,弦振动理论与现代先进的软件和硬件相结合,在许多领域诸如音乐物理学、材料学和系统分析中也都得到了广泛的应用[1].弦振动问题是由弦振动方程附加初边值条件构成的,弦振动方程是一类重要的偏微分方程,它关于时间和空间变量的导数均是二阶的,在解决实际问题的过程中,遇到的弦振动问题通常既有初始条件又有边界条件,是一类混合问题.对于一些简单的混合弦振动问题可以通过分离变量法、叠加原理、齐次化原理及傅里叶变换等方法求其解析解或者是广义解,但是对于一些复杂的弦振动问题,传统的方法求解起来就比较困难,或者求出的解的形式相对复杂,与实际相结合较为困难.这时,就可以通过数值方法进行求解,借助计算机进行辅助分析,从而使求解过程变的轻松,并且能够将所得结果以图形等形式直观地显示出来[3].
文中考虑了以下两端固定的有界弦振动问题

其中,上述问题的解析解可以利用分离变量等方法进行求解[2],但为了更直观地展示上述问题解的形式,以下将采用数值方法进行求解并利用功能强大的Matlab软件进行辅助分析,最后将解析解和数值解进行比较.
1 数值分析
该节首先给出求解问题(1)的有效的数值方法,然后利用这些方法及Matlab软件求出数值解,并且比较几种数值方法的优劣.
1.1 数值方法
求解偏微分方程的数值方法有很多,比较常见的方法就是有限元法和差分法,文献[4]中利用有限元法对(1)进行了求解.文中将利用差分法对(1)进行求解,主要采用显式、隐式两种差分格式.
1.1.1 区域剖分
首先,对定解问题(1)的求解区域W={(x,t)|0<x<l,t>0}进行剖分.在区间[0,1]内取n-1个等分点xi=ih,i=1,…,n-1将区间n等分,其中x0=0,xn=l,h为空间步长.同样,在时间区间内插入若干等分点tj=jτ,j=1,2,…,其中,t0=0,τ为时间步长.用两族平行直线x=xi,1<i<n;t=tj,j=1,2,… 将区域W剖分成矩形网格,其中(xi,tj)为结点,以下将讨论问题(1)在结点处的数值解.
1.1.2 方程离散
用差分方法求解偏微分方程的关键是对方程的离散,下面采用显示、隐式差分格式对问题(1)中方程进行离散,得到如下形式的差分方程.
(i)显示差分方程


(i)隐式差分格式

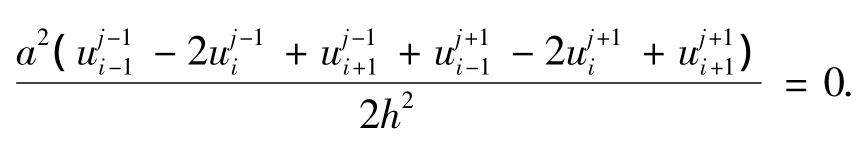
其中i=1,2,…,n-1;j=1,2,…,令则上式可改写为
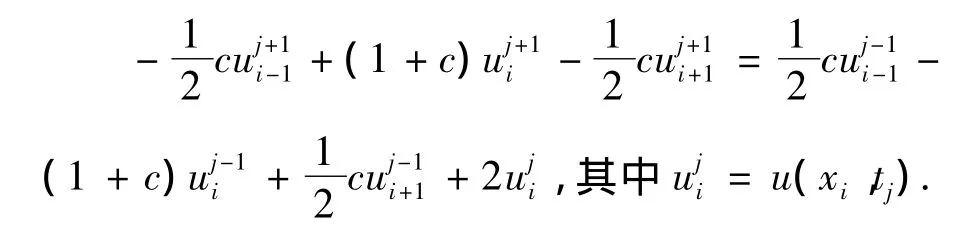
1.1.3 初值条件的处理
问题(1)对应的初值条件可进行如下处理

1.1.4 边值条件的处理
问题(1)对应的边值可进行如下处理
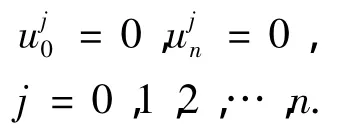
1.2 数值实验
下面将利用计算机实验对问题(1)的数值解进行辅助分析,并将其可视化,实验主要采用的软件是MATLAB软件.
首先,根据显示差分格式编制MATLAB程序模拟问题(1)的数值解,获得动态结果如图1所示.
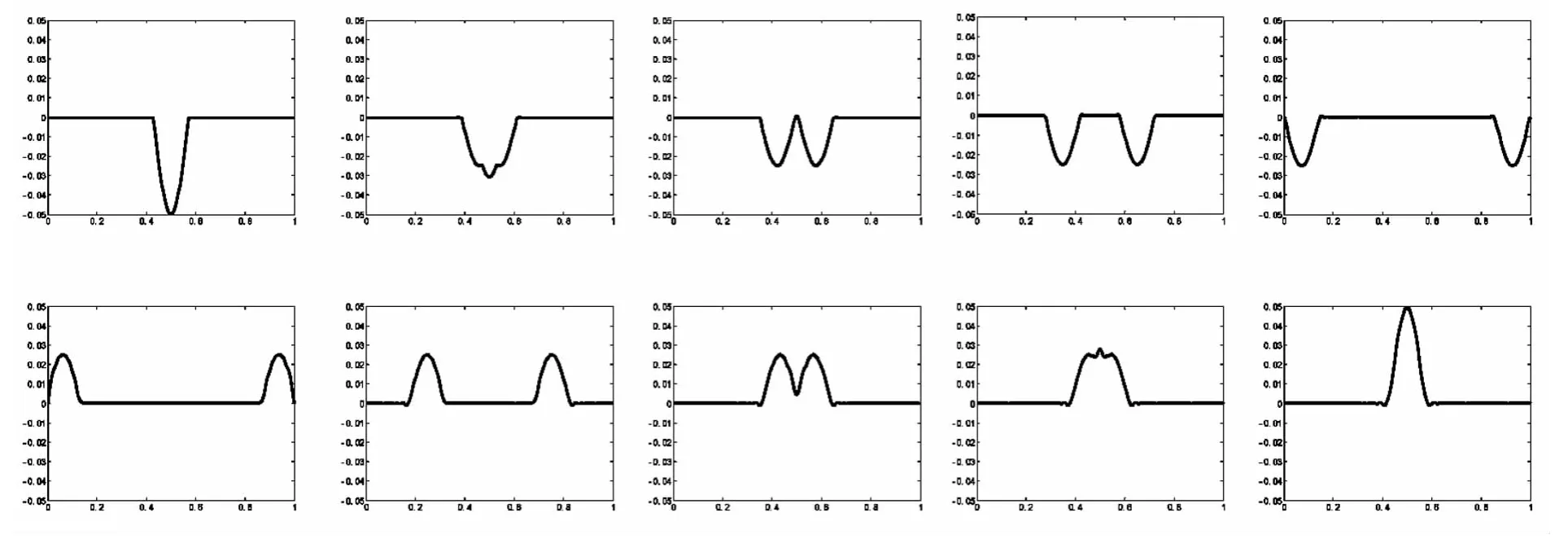
图1
在图1实验中取初始位移为
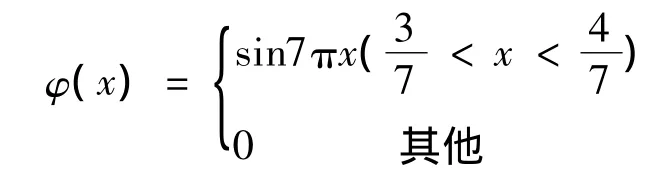
初始速度ψ(x)取为零,时间步长τ=0.0005,空间步长h=0.0024.通过对上述结果进行观察,发现初始状态的波平均分成两个波向相反方向传播,在它们到达弦的端点之前,和波在无限长弦上的传播是一致的,到达弦的端点以后,两个波同时发生反射,出现了半波损失,这是有别于无限长弦的振动的,接下来,被反射回来的两个波进行相向运动并在弦的中间相遇,相遇后两个波叠加继续传播,整个波的传播过程清晰明了,实现了问题(1)的数值解的可视化,有利于进一步研究更为复杂的弦振动问题.
对于问题(1)还可以根据隐式差分格式编制MATLAB程序模拟它的数值解,相应程序的编码要比显示差分格式复杂的多,涉及到三对角方程组的求解等技术性问题,具体程序如下
clear;clc;
format short e
a=1;l=1;n=420;=0.0005;
N=input('请输入运行次数 N的值:');
h = l/n;x = zeros(n+1,1);c =a^2*τ^2/h^2;
for i=1:n
x(i+1)=i*h;
end
u=zeros(n+1,N);
foc i=181:240
u(i,1)=0.05*sin(pi*x(i)*7/l);
u(i,2)=0.05*sin(pi*x(i)*7/l)+1/2*c*0.05*(sin(pi*x(i+1)*7/l)-2*sin(pi*x(i)*7/l) + sin(pi*x(i -1)*7/l));
end
h=plot(x,u(:,1),'linewidth',3);axis([0,1, - 0.05,0.05]);set(h,'EraseMode','xor,'MackecSize',18)
for i=1:N
set(h,'XData',x,'YData',u(:,1));drawnow;
B=zeros(n-1,1);A=zeros(n-2,1);R=zeros(n-2,1);S=zeros(n-1,1);E=zeros(n-1,1);
F=zeros(n-2,1);G=zeros(n-2,1);I=zeros(n-1,1);H=zeros([n-1,n-1]);
for i=1:n-2
E(i)=-(1+c);F(i)=1/2*c;G(i)=1/2*c;I(i)=u(i,1);
end
E(n-1)=-(1+c);H=diag(E)+diag(F,1)+diag(G,-1);I(n-1)=u(n-1,1);J=H*I;
foc i=1:n-2
B(i)=1+c;A(i)=-1/2*c;C(i)=-1/2*c;S(i)=2*u(i,2)+J(i);
end
B(n-1)=1+c;S(n-1)=2*u(n-1,2)+J(n-1);u(1,2)=0;u(n+1,2)=0;S(1)=u(1,2)+J(1);
%追赶法
Y=zecos(n-1,1);X=Y;v=zecos(1,n-1);g=v;v(1)=B(1);Y(1)=S(1);A(2:n-1)=A;
foc i=2:n-1
g(i)=A(i)/v(i-1);v(i)=B(i)-g(i)*C(i-1);Y(i)=S(i)-g(i)*Y(i-1);
end
U=zecos(n-1);L=eye(n-1);
foc i=1:n-2
L(i+1,i)=g(i+1);
end
foc i=1:n-2
U(i,i)=v(i);
U(i,i+1)=C(i);
end
U(n-1,n-1)=v(n-1);X(n-1)=Y(n-1)/v(n-1);foc i=n-2:-1:1
X(i)=(Y(i)-C(i)*X(i+1))/v(i);
end
u(1:n-1,3)=X;u(:,1)=u(:,2);u(:,2)=u(:,3);
end
运行结果的动态展示如图2所示.
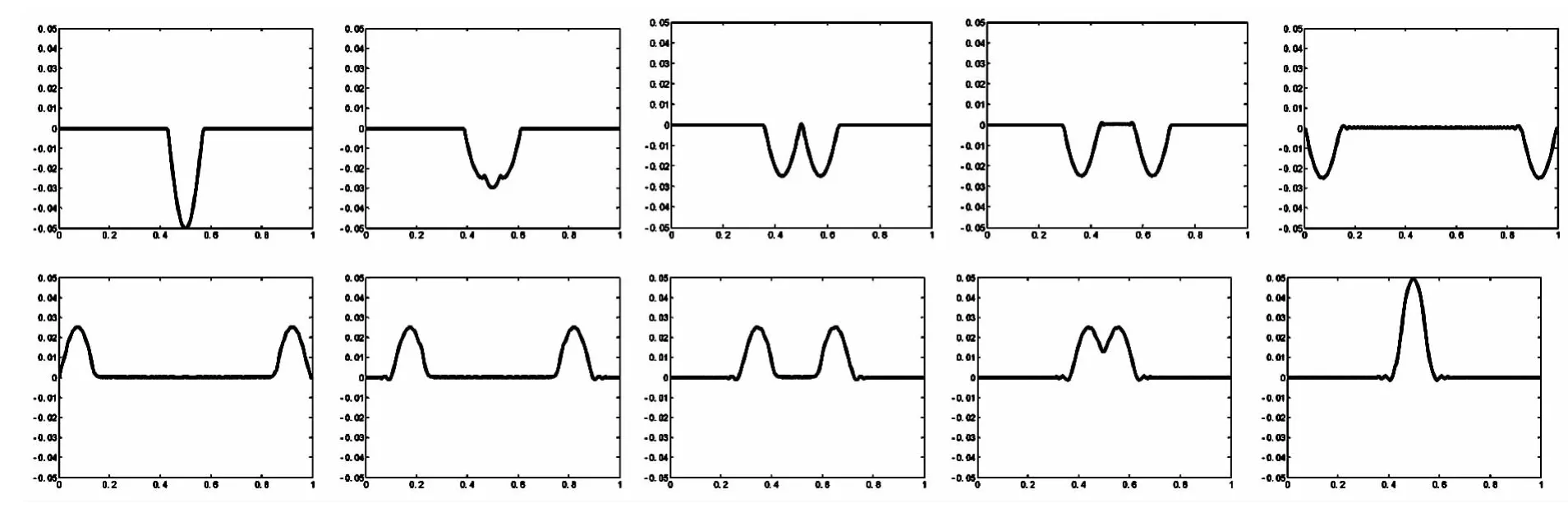
图2
利用隐式差分格式得到的数值结果与显式差分格式总体上是一致的,二者均较好地逼近了解析解[2].
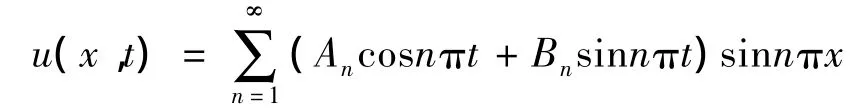
其中的系数是:当n≠7时,
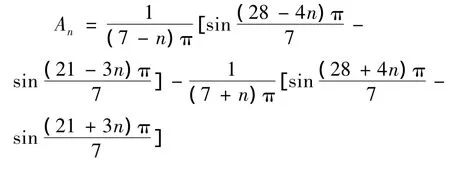
当n=7时另外,B=0.利用MATLABn软件也可以清晰的比较解析解中级数项数的多少对解的精确度的影响,当级数达到50项以上才可以有较高的精确度,另外,根据模拟结果可以观察到解析解中级数的每一项是一个驻波,不同频率的驻波叠加成行波,生动形象.
2 结束语
以上利用MATLAB软件及有限差分方法求解两端固定的有界弦振动问题,首先利用区域转化的思想对方程进行离散,然后编制MATLAB程序进行求解,并将数值解可视化,使对问题(1)的解的物理意义有了更深刻的认识,另外,通过与解析解比较,也充分说明了所选择数值方法的可靠性和计算机辅助分析的重要性.
[1] 李韵,郭怡文,吕郁文.基于 Matlab环境的弦振动方程的图像与音效模拟.科协论坛[J],2009(7):74-75.
[2] 谷超豪,李大潜,等.数学物理方程:第三版[M].北京:高等教育出版社,2012.
[3] 孙丽男,张馥菊.基于MATLAB的一类输运问题的数值分析.哈尔滨师范大学自然科学学报,2012,28(1):14-17.
[4] 高峰,陈君若,等.有界弦振动方程的有限元方法求解[J].机械设计,2008,25(11):15-18.
