巧用分部积分公式计算积分

陈洪波

(哈尔滨师范大学)

0 引言

高等数学是理工科开设的一门重要的必修基础课，在高等数学的教学中，微分与积分是教学重点.积分运算比微分运算困难很多，最主要是积分运算没有一种统一的方法，根据不定积分运算法则和积分公式只能求得一部分简单函数的积分，而对于更广泛的、复杂的函数的不定积分要根据函数的特点选择积分方法.所以，求不定积分有非常大的灵活性.

1 分部积分法

分部积分法是与乘积的微分法相对应的一种方法，是化简被积函数为可求积形式的重要而有效的方法，往往对被积函数是两个基本初等函数的乘积的形式用分部积分法.分部积分法是教学中的重点，也是难点.

首先，要牢记分部积分公式:设u(x)，v(x)具有连续导数，则有分部积分公式

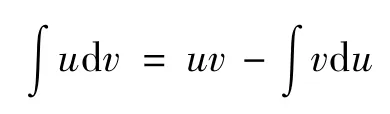
该公式的核心是将左侧积分∫udv转化成右边积分∫vdu.

其次，掌握利用分部积分公式来求积分的过程:

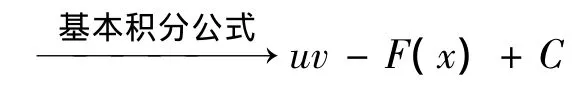
2 使用分部积分法求积分的关键

使用分部积分公式求解积分的关键在于u、dv的选取原则和技巧.

(1)u、dv的选取一般原则:由dv易求出v;比好求.

(2)u的选取优先原则:“反、对、幂、三、指;谁在前u选谁”.

意思是说:由反三角函数、对数函数、幂函数、三角函数、指数函数中任意两个函数的乘积构成的被积函数，一般用分部积分法来求;求积分时，按照“反三角函数 对数函数 幂函数 三角函数指数函数”先后顺序，谁在前u选谁，其余的作为dv.

这样选取的原因是:反三角函数和对数函数的导数是幂函数，使积分∫vdu比∫udv好求解，而三角函数和指数函数的导数仍是他们本身，这样把幂函数排在他们之前选取u，以便于使逐次求导有可能会化简幂函数为常数，有利于我们求积分.

3 典型例题

例1 求∫xarctanxdx

分析 被积函数由“幂函数与反三角函数乘积”构成，u选反三角函数.

解 设u=arctanx，dv=xdx;则 du=则

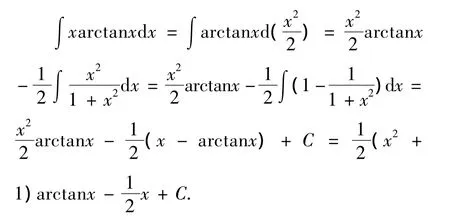
分析 被积函数是“对数函数与幂函数乘积”构成，u选对数函数.

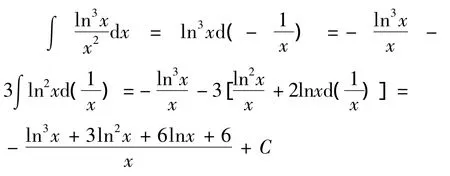
通过上面例题2告诉我们，在积分过程中求解积分时，按照解题需要，可以多次使用分部积分公式.但每一次u和dv的选取要根据具体积分具体选取.

例3 求∫exsinxdx.

分析 被积函数由“三角函数与指数函数乘积”构成，u选三角函数.

解 设u=sinx，dv=exdx;则 du=cosxdx，v=ex

通过上面例题3告诉我们，在积分过程中求解积分时，有些还会出现与原不定积分同类的项，需经移项合并后方能完成求解.

4 结束语

某些函数可能不止一次的应用分部积分公式才能求解，不管用几次公式，只要依据我们总结的u、dv的选取原则，选对u和dv，就能又准又快的求出积分.总之，只要记牢分部积分公式，牢记u、dv的选取原则，就能准确快速的运用分部积分公式求解积分.

［1］ 同济大学应用数学系.高等数学.北京:高等教育出版社，2002.

［2］ 赵树嫄.微积分.北京:中国人民大学出版社，2007.

［3］ 华东师范大学数学系.数学分析.北京:高等教育出版社，2009.

［4］ 四川大学数学学院高等数学教研室.高等数学.北京:高等教育出版社，2009.

［5］ 刘玉莲，傅沛仁.数学分析讲义.北京:高等教育出版社，2006.

［6］ 黄永辉.数学分析选讲.北京:中国铁道出版社，2008.