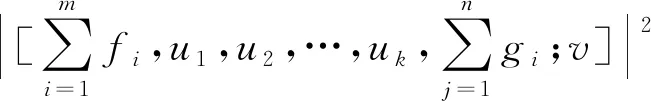四元数Hilbert空间上广义内积与Beckenbach不等式的推广
2020-08-20李会平
李会平
(安徽三联学院基础部,安徽 合肥 230601)
0 引言
内积是泛函分析的重要研究对象,测不准原理是物理上的重要原理。早在1984年,Horwitz和Biedenharn已经开始了测不准原理在四元数与物理问题上的研究[1];最近,关于四元数信号的测不准原理得到关注[2-4]。Beckenbach 不等式与四元数Hilbert空间中的测不准原理有紧密的关系,是研究四元数测不准原理的重要工具[5],因此,为深入研究物理上的测不准原理,很有必要提出广义内积并把Beckenbach不等式推广到广义内积的情形。
1 知识准备
1.1 四元数Hilbert空间
本文用H表示全体四元数,H表示四元数Hilbert空间。先介绍一些四元数Hilbert空间[6]的知识。
设H表示非交换、可结合的四元数实代数,标准基1、i、j、k满足i2=j2=k2=ijk=-1,H中每一个元素可表示为q=x0+x1i+x2j+x3k,其中x0,x1,x2,x3,∈R,q的实部定义为:Re(q)=x0,q的虚部定义为:Im(q)=x1i+x2j+x3k,q的共轭定义为:



(1)〈u,vp+w〉=〈u,v〉p+〈u,w〉,∀p∈ H,∀u,v,w∈H;
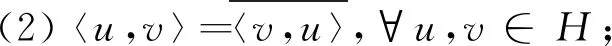
(3)若u∈H,则〈u,u〉≥0,〈u,u〉=0当且仅当u=θ,θ为H中零元素,就称此映射为H-模H上一个Hermitian四元数内积。

范数‖·‖满足三角不等式,即‖u+v‖≤‖u‖+‖v‖,∀u,v∈H.
由范数‖·‖的非负性与三角不等式可知
d(u,v):=‖u-v‖,∀u,v∈H
在H上定义了一个距离。如果距离空间是完备的,就称准Hilbert空间H为Hilbert空间。
注:u与v为H线性相关是指存在q∈H满足u=vq.
Hermitian四元数内积满足标准的Cauchy-Schwarz不等式。
定理1.1 |〈u,v〉|≤‖u‖‖v‖,∀u,v∈H,其中“=”成立,当且仅当u与v为H线性相关。
证: ∀u,v∈H且‖v‖≠0,有u-v〈u,v‖v‖-1〉‖v‖-1⊥v‖v‖-1,

即得|〈u,v〉|≤‖u‖‖v‖.
‖v‖=0时,v=θ,即得|〈u,v〉|=0=‖u‖‖v‖.
如果当u与v为H线性相关,即∃q∈H,u=vq, 那么‖u‖‖v‖=|q|‖v‖2=|〈u,v〉|,即“=”成立。
如果不等式“=”成立,易得u=v〈u,v‖v‖-1〉‖v‖-1或v=0,即u与v为H线性相关。
综上可得不等式成立。
2 广义内积与Beckenbach不等式的推广
2.1 向量数为3的情形
定义2.1.1 设f1,f2,v∈H,称[f1,f2;v]=〈f1,f2〉〈v,v〉-〈f1,v〉〈v,f2〉为3向量f1,f2,v的广义内积。
定理2.1.1 设a1,a2,p∈H,f1,f2,g1,g2,f,v∈H,则下列结论成立,
(2)[f1+f2,g1+g2;v]=[f1,g1;v]+[f1,g2;v]+[f2,g1;v]+[f2,g2;v];
(4)[f,v;v]=0,其中f,v∈H;
(5)[f,f;v]≥0,当且仅当f与v线性相关时“=”成立,其中f,v∈H;

证:(1)[f1a1,f2a2;vp]
=〈f1a1,f2a2〉〈vp,vp〉-〈f1a1,vp〉〈vp,f2a2〉
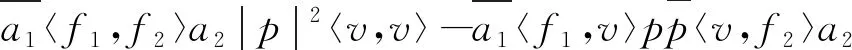
(2)[f1+f2,g1+g2;v]
=〈f1+f2,g1+g2〉〈v,v〉-〈f1+f2,v〉〈v,g1+g2〉
=(〈f1,g1〉+〈f1,g2〉+〈f2,g1〉+〈f2,g2〉)
〈v,v〉-(〈f1,v〉+〈f2,v〉)(〈v,g1〉+〈v,g2〉)
=〈f1,g1〉〈v,v〉-〈f1,v〉〈v,g1〉+〈f1,g2〉
〈v,v〉-〈f1,v〉〈v,g2〉+〈f2,g1〉〈v,v〉-〈f2,v〉
〈v,g1〉+〈f2,g2〉〈v,v〉-〈f2,v〉〈v,g2〉
=〈f1,g1;v〉+〈f1,g2;v〉+〈f2,g1;v〉+〈f2,g2;v〉.
=〈f2,f1〉〈v,v〉-〈f2,v〉〈v,f1〉=[f2,f1;v].
(4)由定义显然.
(5)由Cauchy-Schwarz 不等式有
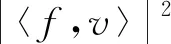
当且仅当f与v线性相关时“=”成立。
政府公共服务必须面向大众而与此同时大众更是服务提供者的监督主体,必须在社会上形成公众参与公共服务的大氛围,公众要了解政府提供公共服务的标准、范围及内容,同时又支持促进公共服务的发展。政府往往提供单一、陈旧的公共服务,不能体察民众之需求,提供的公共服务内容和形式难以与公众对公共服务需求日益增长和改变相适应。
(6)当v=θ时,[f1,f2;v]=[f1,f1;v]=[f2,f2;v]=0,“=”成立.
当v≠θ时,设v‖v‖-1=e∈H,‖e‖=1.取p=〈e,f1〉∈H,q=〈e,f2〉∈H.
即得f1-ep⊥e,f2-eq⊥e.
此时,‖f1‖2=‖(f1-ep)+ep‖2=‖(f1-ep)‖2+‖ep‖2.
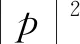
同理可得‖(f2-eq)‖2=[f2,f2;e].

注:定理2.1.1中(6)为Beckenbach不等式推广到3向量广义内积的结论,也为3向量广义内积的Cauchy-Schwarz不等式。
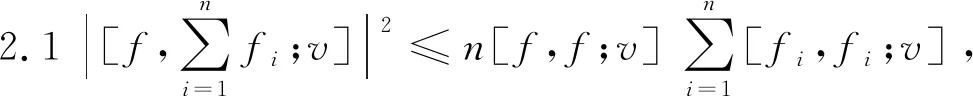
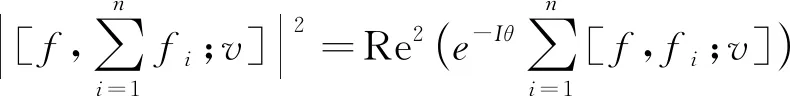
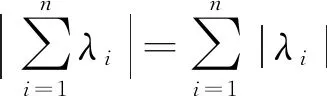
定理2.1.2
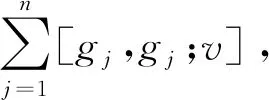
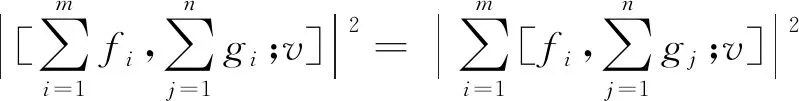
2.2 向量数为4的情形
定义2.2.1设f1,f2,f3,v∈H,称[f1,f2,f3;v]=[f1,f3;v][f2,f2;v]-[f1,f2;v][f2,f3;v]为4向量f1,f2,f3,v的广义内积.
定理2.2.1设a1,a2,a3,p∈H,f1,f2,f3,f,g1,g3,g,v∈H,下列结论成立,
[f1,f2,f3;v]a3;
(2)[f1+g1,f2,f3+g3;v]=[f1,f2,f3;v]+[f1,f2,g3;v]+[g1,f2,f3;v]+[g1,f2,g3;v];
(4)[f,g,v;v]=0,其中f,g,v∈H;
(5)[f,g,f;v]≥0,当且仅当v=θ或f-v〈v,f〉‖v‖-2与g-v〈v,g〉‖v‖-2线性相关时“=”成立,其中f,g,v∈H;
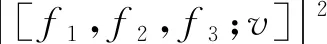
证:(1)[f1a1,f2a2,f3a3;vp]=[f1a1,f3a3;vp]
[f2a2,f2a2;vp]-[f1a1,f2a2;vp][f2a2,f3a3;vp]
(2)[f1+g1,f2,f3+g3;v]=[f1+g1,f3+g3;v]
[f2,f2;v]-[f1+g1,f2;v][f2,f3+g3;v]
={[f1,f3;v]+[f1,g3;v]+[g1,f3;v]+[g1,g3;v]}[f2,f2;v]-{[f1,f2;v]+[g1,f2;v]}{[f2,f3;v]+[f2,g3;v]}
=[f1,f2,f3;v]+[f1,f2,g3;v]+[g1,f2,f3;v]+[g1,f2,g3;v].
=[f2,f2;v][f3,f1;v]-[f3,f2;v][f2,f1;v]
=[f3,f2,f1;v].
(4)由定义显然.
(5)由定理2.1.1中(6)即得
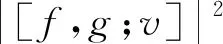
仅当v=θ或f-v〈v,f〉‖v‖-2与g-v〈v,g〉 ‖v‖-2线性相关时“=”成立,其中f,g,v∈H.
(6)由定理2.1.1中(6),对∀p∈R,q∈H;f1,f2,f3,v∈H,有
[f1p+f3q,f1p+f3q;v][f2,f2;v]-[f1p+f3q,f2;v][f2,f1p+f3q;v]≥0.
即得
即得
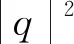
当[f1,f1;v][f2,f2;v]-[f1,f2;v][f2,f1;v]>0时,由上式对∀p∈R成立有
Re2{[f1,f3;v][f2,f2;v]q-[f1,f2;v][f2,f3;v]q}≤{[f1,f1;v][f2,f2;v]-[f1,f2;v][f2,f1;v]}
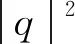
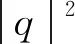


当[f1,f1;v][f2,f2;v]-[f1,f2;v][f2,f1;v]=0时,即[f1,f2,f1;v]=0,由定理2.1.1有v=θ或f1-v〈v,f1〉‖v‖-2与f2-v〈v,f2〉‖v‖-2线性相关。

[f1,f2,f3;v]=[f1,(f1-v〈v,f1〉‖v‖-2)k+v〈v,f2〉‖v‖-2,f3;v]=0,

当v=θ或f1-v〈v,f1〉‖v‖-2与f3-v〈v,f3〉
‖v‖-2线性相关时,设
f3=(f1-v〈v,f1〉‖v‖-2)k+v〈v,f3〉
‖v‖-2,k∈H,
经计算可得


注:定理2.2.1中(6)为Beckenbach不等式推广到4向量广义内积的结论,也为4向量广义内积的Cauchy-Schwarz不等式。
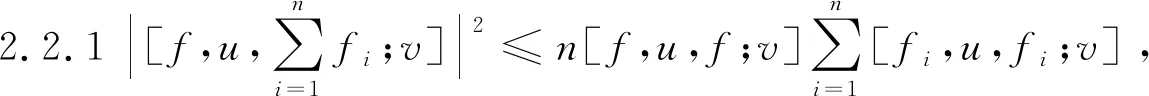
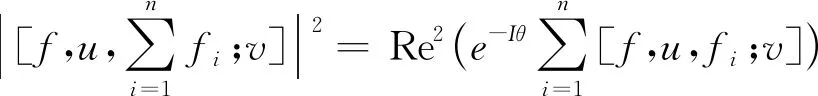
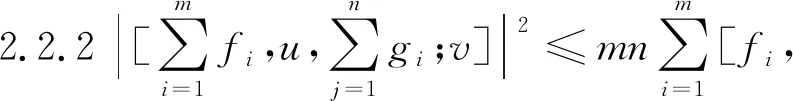
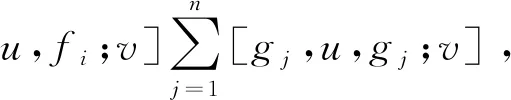
证:
其中f1,f2,…,fm,g1,g2,…,n,u,v∈H.
2.3 向量数为m(m>3)的情形
一般地可以给出n+2个向量的内积。
定义2.3.1设n>1且n∈N+,f1,f2,…,fn,fn+1,v∈H,称
[f1,f2,…,fn,fn+1;v]=[f1,f2,…,fn-1,fn+1;v][fn,f2,…,fn-1,fn;v]-[f1,f2,…,fn-1,fn;v][fn,f2,…,fn-1,fn+1;v]
为n+2个向量f1,f2,…,fn,fn+1,v的广义内积。
n∈N+,n≥1,n+2个向量内积都称为广义内积。
定理2.3.1设n>1且n∈N+,a1,a2,…,an,p∈H,f1,f2,…,fn,g1,gn,v∈H,下列结论成立,
(1)[f1a1,f2a2,…,fn-1an-1,fnan;vp]
(2)[f1+g1,f2,…,fn-1,fn+gn;v]
=[f1,f2,…,fn-1,fn;v]+[f1,f2,…,fn-1,gn;v]+[g1,f2,…,fn-1,fn;v]+[g1,f2,…,fn-1,gn;v];
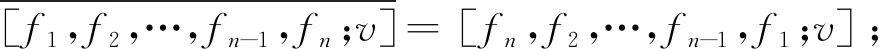
(4)[f1,f2,…,fn-1,v;v]=0;
(5)[f1,f2,…,fn-1,f1;v]≥0;

≤[f1,f2,…,fn-1,f1;v][fn,f2,…,fn-1,fn;v],
当v=θ或f1-v〈v,f1〉‖v‖-2与fn-v
〈v,fn〉‖v‖-2线性相关时“=”成立。
证:n=2,由定理2.1.1得结论成立;
n=3,由定理2.2.1得结论成立;
假设n=k>1且k∈N+时,结论成立,即假设以下(1)′—(6)′成立,
(1)′[f1a1,f2a2,…,fk-1ak-1,fkak;vp]
(2)′[f1+g1,f2,…,fk-1,fk+gk;v]
=[f1,f2,…,fk-1,fk;v]+[f1,f2,…,fk-1,gk;v]+[g1,f2,…,fk-1,fk;v]+[g1,f2,…,fk-1,gk;v];
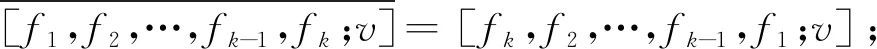
(4)′[f1,f2,…,fk-1,v;v]=0;
(5)′[f1,f2,…,fk-1,f1;v]≥0;

[fk,f2,…,fk-1,fk;v],当且仅当v=θ或f1-v〈v,f1〉‖v‖-2与fk-v〈v,fk〉‖v‖-2线性相关时“=”成立。
以下证当n=k+1时,(1)—(6)成立。
当n=k+1时,[f1a1,f2a2,…,fkak,fk+1ak+1;vp]
=[f1a1,f2a2,…,fk-1ak-1,fk+1ak+1;vp][fkak,f2a2,…,fk-1ak-1,fkak;vp]-[f1a1,f2a2,…,fk-1ak-1,fkak;vp][fkak,f2a2,…,fk-1ak-1,fk+1ak+1;vp]
即对n>1,(1)成立。
当n=k+1时,
[f1+g1,f2,…,fk,fk+1+gk+1;v]
=[f1+g1,f2,…,fk-1,fk+1+gk+1;v][fk,f2,…,fk-1,fk;v]-[f1+g1,f2,…,fk-1,fk;v][fk,f2,…,fk-1,fk+1+gk+1;v]
=([f1,f2,…,fk-1,fk+1;v]+[f1,f2,…,fk-1,gk+1;v]+[g1,f2,…,fk-1,fk+1;v]+[g1,f2,…,fk-1,gk+1;v])
[fk,f2,…,fk-1,fk;v]-([f1,f2,…,fk-1,fk;v]+
[g1,f2,…,fk-1,fk;v])([fk,f2,…,fk-1,fk+1;v]+
[fk,f2,…,fk-1,gk+1;v])
=[f1,f2,…,fk,fk+1;v]+[f1,f2,…,fk,gk+1;v]+[g1,f2,…,fk,fk+1;v]+[g1,f2,…,fk,gk+1;v]
即对n>1,(2)成立。
当n=k+1时,
=[fk+1,f2,…,fk-1,f1;v][fk,f2,…,fk-1,fk;v]-
[fk+1,f2,…,fk-1,fk;v][fk,f2,…,fk-1,f1;v]
=[fk+1,f2,…,fk-1,fk,f1;v]
即对n>1,(3)成立。
当n=k+1时,
[f1,f2,…,fk-1,fk,v;v]
=[f1,f2,…,fk-1,v;v][fk,f2,…,fk-1,fk;v]-
[f1,f2,…,fk-1,fk;v][fk,f2,…,fk-1,v;v]
=0
即对n>1,(4)成立。
当n=k+1时,
[f1,f2,…,fk-1,fk,f1;v]
=[f1,f2,…,fk-1,f1;v][fk,f2,…,fk-1,fk;v]-
[f1,f2,…,fk-1,fk;v][fk,f2,…,fk-1,f1;v]
≥0
即对n>1,(5)成立。
当n=k+1时,只要证
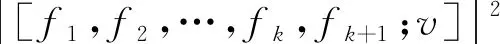
[fk+1,f2,…,fk,fk+1;v],当且仅当v=0或f1-v〈v,f1〉‖v‖-2与fk+1-v〈v,fk+1〉‖v‖-2线性相关时“=”成立。
由归纳假设,对∀p∈R,q∈H;f1,f2,…,fk+1,v∈H,有
[f1p+fk+1q,f2,…,fk-1,f1p+fk+1q;v]
[fk,f2,…,fk-1,fk;v]-[f1p+fk+1q,f2,…,fk;v]
[fk,f2,…,fk-1,f1p+fk+1q;v]≥0,
即得
([fk,f2,…,fk-1,f1;v]p+[fk,f2,…,fk-1,fk+1;v]q)≥0,
即得
{[f1,f2,…,fk-1,f1;v][fk,f2,…,fk-1,fk;v]
-[f1,f2,…,fk;v][fk,f2,…,fk,f1;v]}p2
+2Re{[f1,f2,…,fk-1,fk+1;v][fk,f2,…,fk-1,fk;v]q
-[f1,f2,…,fk;v][fk,f2,…,fk-1,fk+1;v]q}p
+{[fk+1,f2,…,fk-1,fk+1;v][fk,f2,…,fk-1,fk;v]
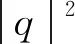
当[f1,f2,…,fk-1,f1;v][fk,f2,…,fk-1,fk;v]
>[f1,f2,…,fk-1,fk;v][fk,f2,…,fk,f1;v]时,
由上式对∀p∈R成立有
Re2{[f1,f2,…,fk-1,fk+1;v][fk,f2,…,fk-1,fk;v]q-[f1,f2,…,fk,;v][fk,f2,…,fk,fk+1;v]q}
≤{[f1,f2,…,fk-1,f1;v][fk,f2,…,fk-1,fk;v]-
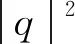
即得Re2{[f1,f2,…,fk,fk+1;v]q}
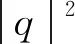
取q=[fk+1,f2,…,fk,f1;v]≠0,有

[fk+1,f2,…,fk,fk+1;v].
取q=[fk+1,f2,…,fk,f1;v]=0,有
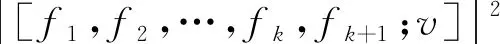
[fk+1,f2,…,fk+1,fk+1;v].
当[f1,f2,…,fk-1,f1;v][fk,f2,…,fk-1,fk;v]=[f1,f2,…,fk-1,fk;v][fk,f2,…,fk-1,f1;v]时,由归纳假设当且仅当v=θ或f1-v〈v,f1〉‖v‖-2与fk-v〈v,fk〉‖v‖-2线性相关时“=”成立。
即[f1,f2,…,fk,f1;v]=0,当且仅当v=θ或f1-v〈v,f1〉‖v‖-2与fk-v〈v,fk〉‖v‖-2线性相关时“=”成立。
此时由广义内积定义与v=θ或f1-v〈v,f1〉‖v‖-2与fk-v〈v,fk〉‖v‖-2线性相关经计算得
[f1,f2,…,fk,fk+1;v]=0,
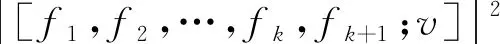
[fk+1,f2,…,fk,fk+1;v]=0.
当v=θ或f1-v〈v,f1〉‖v‖-2与fk+1-v〈v,fk+1〉‖v‖-2线性相关时,设
fk+1=(f1-v〈v,f1〉‖v‖-2)λ+v〈v,fk+1〉 ‖v‖-2,λ∈H,经计算可得
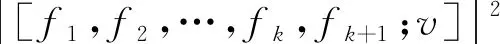
[fk+1,f2,…,fk,fk+1;v].
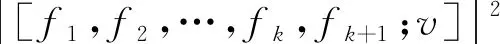
其中f1,f2,…,fk+1,v∈H.
即对n>1,(6)成立。
综上可知定理成立。
注:定理2.3.1中(6)为Beckenbach不等式推广到n向量广义内积的结论,也为n向量广义内积的Cauchy-Schwarz不等式。
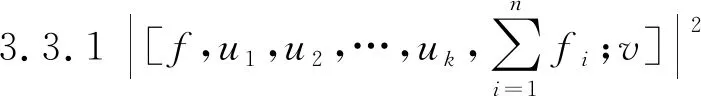
其中f,f1,f2,…,fn,u1,u2,…,uk,v∈H.
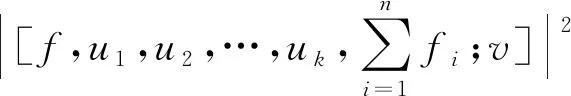
v])|2,fi;v]).
v])|2,fi;v])