时滞比率依赖种群模型Hopf-Fold分支现象分析
2014-09-17夏晶,郭爽
夏 晶 ,郭 爽
(大庆师范学院)
0 引言
1977年,Freedman和 Waltman在文献[1]中提出了一类三维捕食-食饵模型:

这里x(t),y(t)和z(t)分别表示t时刻食饵,捕食者和顶层捕食者的数量;g(x)是食饵的内部增长函数;p(x)和q(x)分别是捕食者和顶层捕食者的功能反应增长函数;h,s>0分别是捕食者和顶层捕食者的死亡率;e,m>0分别是食饵和捕食者的转换率.许多作者对该模型进行了研究,具体参见文献[2-7].该文主要针对顶层捕食者方程中含有时滞项的情形进行分析,对该模型能否发生Hopf-Fold分支现象进行讨论.
1 Hopf-Fold分支
该文研究的模型如下:

对方程(2)进行非量纲化处理,得到:
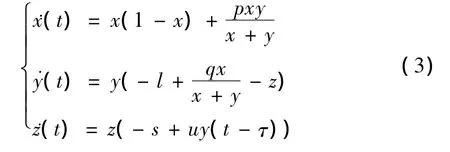
其中x0(θ)=φ1(θ)≥0,y0(θ)=φ2(θ)≥0,z0(θ)=φ3(θ)≥ 0,θ∈ [-τ,0],x(0)>0,y(0)>0,z(0)>0,‖φ‖ =max{|φ(θ)|:θ∈[τ,0]},φ(θ)=(φ1,φ2,φ3)∈C([-1,0],R3)及这里a,k,c,m,d,f,r,s,e都是正参数.假设方程(3)的正平衡点存在,并记为E*(x*,y*,z*),其中

在E*处考虑相应的线性化系统,特征值λ满足如下的特征方程:

其中:a2=-m11-m22,a1=m11m22-m12m21,b1=m23m32andb0=m11m23n32.以及
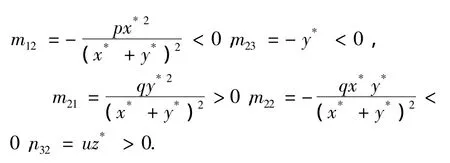
当m11=0时,有b0=0,易知λ=0是方程(4)的一个零根,同时:

这就意味着当a1+b1<0时,λ=0是方程(4)的一个单零特征根.
接下来把λ=iω代入到方程(4)中,分离实虚部得:

将其化简得:

令ω2=l及h(l)=l2+(a22-2a1)l+(a21-b21),所以方程(4)就至少有一个正根ω0,同时由(5)式有:

记

所以(±iω0,τ0)是方程(4)的解.
记λ(τ)=α(τ)+iω(τ)是方程(4)满足α(τ0)=0,ω(τ0)=ω0的根,定义,于是当p=p*,τ=τ0时,有下述定理成立:
定理:若a1+b1<0,当p=p*,τ=τ0,时,方程(4)的特征根除了λ=0和λ=±iω0外,其余特征根都具有负实部.
证明 根据前面的分析,当p=p*,τ=τ0时,方程(4)有一个单零特征根和一对纯虚根.假设方程(4)还具有正实部的特征根,并记为λ=α0+iβ0,那么λ=α(τ)+iβ(τ)就是方程(4)在p=p*和τ=τ0时满足α(τ0)=α0>0和β(τ0)=β0的根.于是存在一个正数0<ζ<τ0,使得当τ∈(τ0-ζ,τ0)时,有α(τ)>0 成立.
当τ=0时,D(λ,0)=λ3+a2λ2+(a1+b1)λ=0有一个单零特征根和一对纯虚根.进一步:

矛盾.证毕.
2 数值模拟
选择以下参数值进行数值模拟:a=0.312,b=0.171,c=0.360,r=0.312,s=0.123,d=0.396,l=0.571,通过简单的计算,有p*=1.247,τ0=2.186,以(p*,τ0)为分支点,选取三组不同的参数值(p,τ)=(0.467,1.4767),(2.165,3.178)及 (3.997,10.608),对应着不同的波动曲线如图1—图3所示.

图1 当p=0.467,τ =1.4767时,平衡点E*(x*,y*,z*)的波动图

图2 当p=2.165,τ =3.178时,平衡点E*(x*,y*,z*)的附近的周期波动图

图3 当p=3.997,τ=10.608时,平衡点附近的爆发行为
当零和一对纯虚根都是这个时滞系统的特征值时会发生Hopf-Fold分支现象.因此,把(p*,τ0)作为分支点,模型(3)的平衡点E*(x*,y*,z*)就会经历Hopf-Fold分支,随着参数的变化,就会出现一些有趣的现象如周期行为、拟周期行为或爆发行为等.
[1] Freedman H I,Waltman P.Mathematical analysis of some three-species food-chain models[J].Mathematical Biosciences,1977,3(33):257-276.
[2] Ginoux J M,Rossetto B,Jamet J L.Chaos in a three-dimensional Volterra-Gause model of predator-prey type.2005,5(15):1689-1708.
[3] Hastings A,Powell T.Ecology.Chaos in three-species food chain [J].International Journal of Bifurcation and Chaos,1991,3(72):896-903.
[4] 郭爽,刘洋,沙元霞,于键.Cause型捕食模型的稳定性与分支分析[J].吉林大学学报(理学版),2012,5(50):940-944.
[5] FariaT,MagalhvesLT.Restrictionson the Possible Flows of Scalar Retarded Functional Differential Equations in Neighborhoods of Singularities[J].Journal Dynamics and Differential Equations,1996,8(1):35-70.
[6] 刘振杰,徐亚兰,钮佩琨.一类具有稀疏效应的捕食者-食饵系统的周期解[J].哈尔滨师范大学自然科学学报,2006,6(22):4-6.
[7] 欧伯群,秦发金.基于比率的离散型Leslie系统正周期解的存在性[J].哈尔滨师范大学自然科学学报,2006,6(22):7-10.
