Banach空间中的一类广义太阳集及其相互关系*

关伟波，李言睿，李 燕

(1.哈尔滨师范大学;2.中国石油大学)

0 引言

设X是实Banach空间，X*为其对偶空间，设C是X的一个子集.集值映射PC(x)={z∈C:}被称为集值度量投影算子.若任意x∈X，∈PC(x)有∈PC(xt)，其中xt=+t()，0≤t.则称是C的太阳点.若C中的任意一点都是C的太阳点，则称C是太阳集.太阳集的概念是由 Efimov，Stechkin［4］首先引入的.

Banach空间X上的对偶映射J:X→X*定义为:J(x)={x∈X*|(x*，x)=‖x*‖2=‖x‖2}.

下面列出对偶映射J的一些性质［1，2，7］:

①X是自反的当且仅当J是满射;②X是严格凸的当且仅当J是单射;③X是光滑的当且仅当J是单值映射;④在光滑的

Banach空间中，J是范-弱星连续的，即xn→x蕴涵Jx;⑤在Frechet光滑的Banach空间中，J是范-范连续的，即xn→x蕴涵Jxn→Jx;⑥任意x∈X，a∈R，J(a x)=a J(x).

在X为光滑Banach空间的情况下，文献引进函数W(x，y):= ‖x‖2-2〈Jx，y〉+‖y‖2，x，y∈X.容易验证(‖x‖-‖y‖)2≤W(x，y)≤(‖x‖+‖y‖)2.

基于函数Alber W(1994)在一致凸和一致光滑的Banach空间中引入广义投影算子∏C:X→C，即∏C(x)=argminy∈CW(x，y)，并且详细研究其性质.容易看到，在 Hilbert空间中，∏C=PC.

在文献［8］中，作者将太阳集的概念推广到广义的W-太阳集，也就是，设X为自反且光滑的Banach空间，C是X的子集.称∈C是C的W-太阳点是指，对任意x∈X，若∈∏C(x)，则∈∏C(xt)，任意t≥0，其中xt∈X满足J(xt)=(1-t)若C中的每一点都是C的W-太阳点，则称C是W-太阳集.

下面列出几个关于W-太阳集的事实(见文献［8］):设X为自反且光滑的Banach空间，C是X的子集.①是C的W-太阳点当且仅当对任意x∈X，若∈∏C(x)，则∈∏C(x2)，其中x2∈X满足Jx2=2;②若C是Banach空间X中的凸集，则C是W-太阳集.

还需要下面的定义和引理:

引理1［4］设C是自反且光滑Banach空间X的一个子集，若∈∏C(x)，则∈∏C(xt)，其中xt∈X满足J(xt)=(1-t)，0≤t≤ 1.

定义1［5］C是W-迫近的是指任意x∈X，∏C(x)是非空集合;C是半W-Chebyshev的是指任意x∈X，∏C(x)至多是单点集;C是WChebyshev的是指C是W-迫近的且是半WChebyshev的.

1 主要结果

命题1.1 设X为自反、严格凸且光滑的Banach空间，C是X的子集.令x∈X，∈C.若∈∏C(x)，则{}=∏C(xt)，其中任意0≤t≤1，xt∈X满足J(xt)=(1-t)

证明∈∏C(xt)由引理1可得，现证明唯一性.假设存在∈∏C(xt)，则W(x，)=W(xt，)，也就是

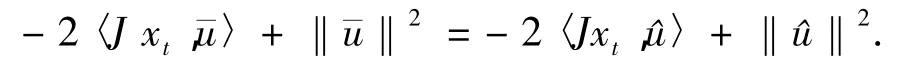
整理得-2〈(1-t)，〉+‖‖2=-2〈(1-t)，〉+‖‖2

进一步整理得t［-2〈Jx，〉+2〈Jx，〉+‖‖2-‖‖2］=(1-t)［‖‖2+‖‖2-2〈，〉］

也就是

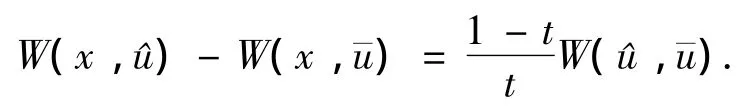
若≠则由严格凸性可知W(，)＞0进而W(x，)＞W(x，)这与∈∏C(x)相矛盾.

命题1.2 若X是自反严格凸且光滑的Banach空间，C是X的子集，则cl(U)=X*.其中U={Jx∈X*:∏C(x)至多是单点集}.

证明 对任意x∈X，若∏C(x)至多是单点集，则Jx∈U.因此Jx∈cl(U).若∏C(x)不是至多单点集，则存在1，2∈C，使得1≠2且1，2∈ ∏C(x).由 命 题 1.1 可 知{1}=∏C(xt)，任意0＜t＜1，其中xt∈X满足

J(xt)=(1-t)1+tJx.也就是存在(1-t)1+tJx∈U使得=Jx.即Jx∈cl(U).

定义1.1 设X为自反且光滑的Banach空间，C是X的子集.称C是Ⅰ-太阳集是指，对任意x∉C，存在∈∏C(x)，使得∈∏C(xt)，任意t≥0，其中xt∈X满足

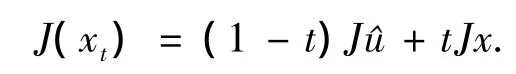
定义1.2 设X为自反且光滑的Banach空间，C是X的W-迫近子集.称C是Ⅱ-太阳集是指，对任意x∉C，任意∈∏C(x)，使得∈∏C(xt)，任意t≥0，其中xt∈X满足J(xt)=(1-t)

定义1.3 设X为自反且光滑的Banach空间，C是X的子集.称C是Ⅲ-太阳集是指，对任意x∉C，任意r＞0，存在z∈X，∈∏C(z)使得 ‖z‖2-‖x‖2+2〈Jx-Jz，〉=r其中J(x)=(1-t)，0 ≤t≤1.

定义1.4 设X为自反且光滑的Banach空间，C是X的子集.称C是Ⅳ-太阳集是指，对任意x∉C，存在z∈X，∈∏C(z)使得J(x)=(1-t)，0＜t＜1.

注记 Ⅱ-太阳集是W-太阳集，Ⅱ-太阳集是Ⅰ-太阳集，Ⅰ-太阳集是Ⅲ-太阳集，Ⅲ-太阳集是Ⅳ-太阳集.若C是自反且光滑Banach空间中的W-Chebyshev集，则Ⅰ-太阳集是Ⅱ-太阳集.

例 在自反且光滑的Banach空间中，闭凸集是Ⅱ-太阳集.

命题1.3 设X为自反且光滑的Banach空间，C是X的子集.若C是W-Chebyshev的Ⅳ-太阳集，则C是Ⅰ-太阳集.

证明 对任意y∉C，∈∏C(y)，由连续函数的性质有集合M={z:∈∏C(z)，z=(1-t)，t≥0}在N={(1-t):t≥0}上是闭集.但是由C是Ⅳ-太阳集知集合M在N上是开集.因此M=N.

命题1.4 设X为自反且Frechet光滑的Banach空间，C⊂X是Ⅲ-太阳集.若广义投影算子∏C连续且对任意x∈X，∏C(x)是紧集，则C是Ⅰ-太阳集.

证明 对任意x∉C，任意n＞0，存在zn∈X，yn∈∏C(zn)使得‖zn‖2-‖x‖2+2〈Jx-Jzn，yn〉=n其中J(x)=(1-tn)Jzn+tnJyn，0 ≤tn≤1.由引理1有，yn∈∏C(x).因为∏

C(x)是紧集，所以{yn}存在收敛子列(不妨令其为本身)，使得yn→y0∈∏C(x).

设任意r＞0，令Jz=r‖Jx-Jy0‖-1(Jx-Jy0)+Jx，Jzn'=r‖Jx-Jyn‖-1(Jx-Jyn)+Jx，Jzn=n‖Jx-Jyn‖-1(Jx-Jyn)+Jx.当n≥r时，有.由引理1 得

由yn→y0和X是Frechet光滑的，有Jzn'→Jz.进而由引理1 可知另一方面由yn→y0有W→W(z，y0)即

定义1.5［3］在光滑的Banach空间X中，若蕴涵，则称对偶映射J是弱连续.

定义1.6［6，9］集值映射F:X→2X的上图{(x，y):y∈F(x)}是弱闭的是指蕴涵y∈F(x).

命题1.5 设X为自反、严格凸且光滑的Banach空间，C⊂X是Ⅲ-太阳集.若对偶映射J和J*弱连续，∏C的上图弱闭且对任意x∈X，∏C(x)是弱紧集，则C是Ⅰ-太阳集.

证明 对任意x∉C，任意n＞0，存在zn∈X，yn∈ ∏C(zn)使得 ‖Jx-Jzn‖=n其中J(x)=(1-tn)Jzn+tnJyn，0 ≤tn≤ 1.由命题1.1有，yn∈∏C(x).因为∏C(x)是弱紧集，所以{yn}存在弱收敛子列(不妨令其为本身)，使得∈∏(x).设任意r＞0令Jz=

［1］ Alber Y I.Generalized projection operators in Banach spaces:properties and applications，in:Proceedings of the Israel Seminar，Ariel Israel Functional Differ.Equ，1994(1):1-21.

［2］ Alber Y I.Generalized projection operators in Banach spaces:properties and applications，in:Theory and Applications of Nonlinear Operators of Accretive and Monotone Type(A Kartsatos，Ed)，Marcel Dekker，Inc，1996.15-50.

［3］ Diestel J.Geometry of Banach Space-Selected Topics，Lecture Notes in Math.Springer-Verlag，Berlin，1975.

［4］ Efimov N V，Stechkin S B.Some properties of Chebyshev sets.Dokl Akad Nauk SSSR，1958，118:17-19.

［5］ Guan W B，Song W.W-approximative Compactness and Continuity of the Generalized Projection Operator in Banach Spaces.Journal of Approximation Theory，2010，162:64-71.

［6］ Singer I.Theory of best Approximation and Functional Analysis.Springer-Verlag，New York，1970.

［7］ Song W，Cao Z J.The generalized decomposition theorem in Banach spaces and its applications.Journal of Approximation Theory，2004，129:167-181.

［8］ 关伟波，宋文.Banach空间中的弱凸集和W-太阳集.数学学报，2010，531:45-50.

［9］ 徐士英，李冲，杨文善.Banach空间中的非线性逼近理论.科学出版社，1997.