渐近拟非扩张型映射的公共不动点
2014-09-17刘辉
刘 辉
(黑龙江财经学院)
0 引言
设E是实Banach空间,C是非空闭凸集C⊂E,F(T)是映射T的公共不动点集合.
定义1[1]设E是一个实Banach空间,C是E上的非空凸子集.
(1)如果映象P满足如果P2=P,则称P是从E到C的一个收缩核映射.
(2)称E的子集C为E的收缩核,如存在连续的收缩映射满足Px=x,∀x∈C.
(3)称C为E上的非扩张收缩核,如存在非扩张收缩映象P:E→C满足Px=x,∀x∈C.
定义2[1]设E是实Banach空间,C为E上的非空非扩张收缩核,P为从E到C的非扩张收缩映象.设T:E→C为非自映象.
(1)称T为非自渐近非扩张映象,如果存在序列{kn}⊂[1,∞),满足kn→ 1(n→ ∞),‖T(PT)n-1x-T(PT)n-1y‖≤kn‖x-y‖,∀x,y∈C,n≥1.
(2)T称为非自渐近拟非扩张映象,若F(T)≠φ,若存在序列{kn}⊂[1,∞)且kn→1(n→∞)满足:

(3)T称为非自渐近非扩张型映象,若
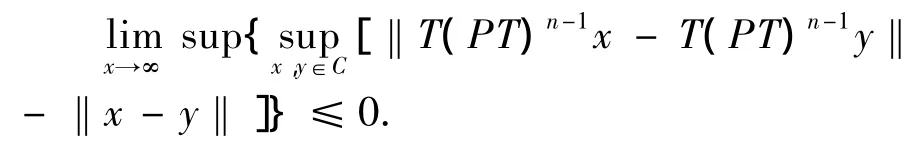
(4)T称为非自渐近拟非扩张型映象,若F(T)≠φ使得

定义3 设E为实Banach空间,C为E的非空凸子集满足C是E上的收缩核,P:E→C的保核收缩映象,T1,T2,…,TN为C到E上的非自渐近拟非扩张型映象,∀x1∈C,具有误差的N步迭代序列{xn}如下:

引理1[2]{an}{bn}为满足下面条件的两个非负实数列:
an+1≤an+bn,∀n≥1,其中,则存在.
1 有误差的N步非自渐近拟非扩张型映象序列的收敛性
定理1 设E是Banach空间,C是E上非空闭凸子集且为E上的收缩核,P:E→C的保核收缩映象,T1,T2,…,TN为C到E上的非自渐近非扩张型映象,i=1,2,…,N是C上的有界列,i=1,2,…,N是[0,1]满足<∞ ,i=1,2,…,N则 (1)所定义的序列{xn}强收敛于T1,T2,…,TN的公共不动点的充要条件为
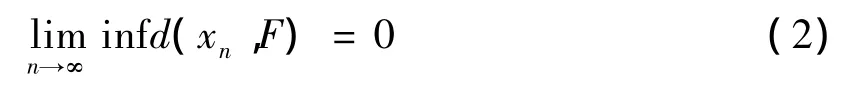
证明 (必要性)显然.
(充分性)设T1,T2,…,TN为C到E上的非自渐近拟非扩张型映象,故∀ε>0,存在正整数n0使得当n≥n0时,有

由于{xn},{yni}⊂C,i=1,2,…,N-1,对任意n≥n0有

由(1)和(4)有

类似的我们也可证明:

由(6)和(7)有

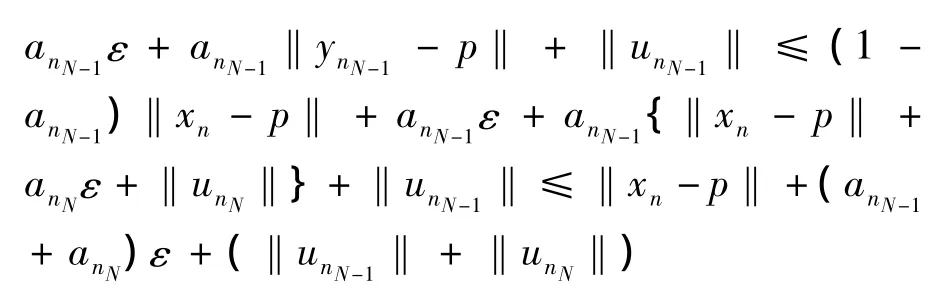
由归纳法,可以证明对任意
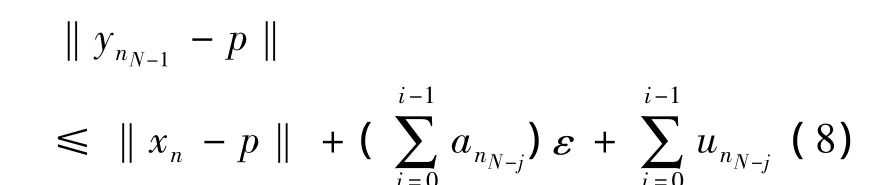
特别地在(8)取i=n-1,有

因此由(5)和(9)有
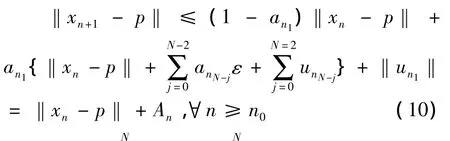

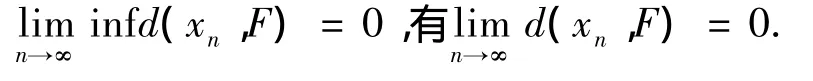
下证(1)所确定的序列{xn}是柯西列,事实上,对 ∀n≥n0,∀m≥1,∀p∈F,从(10)有
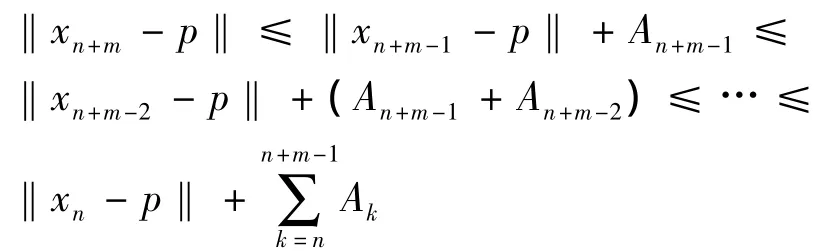
此对n≥n0,m≥1,‖xn+m-xn‖ ≤
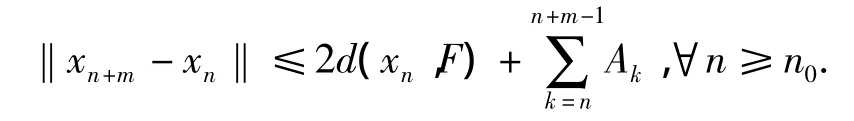
由P的任意性,有
因此‖xn+m-xn‖<ε,因此对任意m≥1,有= 0,这就说明{xn}在C中是柯西列,又因C是E上的闭子集,因此是完备的,因此存在P*∈C,使得xn→p*(n→∞).
最后,证明p*∈F(反证),假定p*∉F.因为F是闭集,d(p*,F)>0,因此对任意p∈F,有‖p*-p‖≤‖p*-xn‖+‖xn-p‖,让n→∞,有d(p*,F)≤0,矛盾,因此p*∈F.
注意:容易证明,若在定理1的T1,T2,…,Tn:C→E是连续的,则T1,T2,…,TN的公共不动点集F是闭集.
推论1 设E是一实Banach空间,C是E上非空闭凸子集且为E上的收缩核,P:E→C的保核收缩映象,设T1,T2,…,TN为C到E上的非自渐近拟非扩张映象,且是非空闭集.其中,…,N是C上的N个有界序列,i=1,2,…,N=1,2,…,N.是[0,1]上的序列且满足:
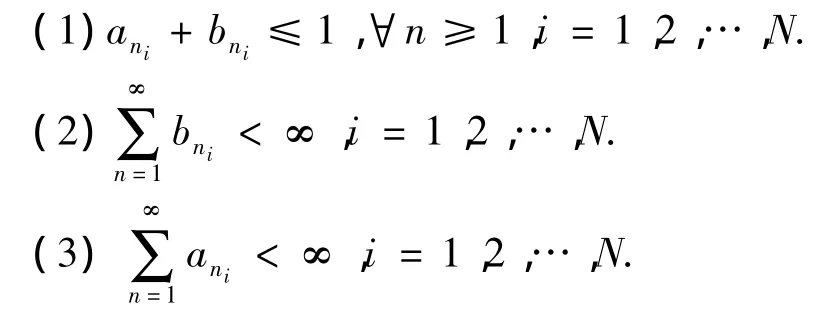
则(1)所定义的序列{xn}强收敛于T1,T2,…,TN的公共不动点的充分必要条件为:
证明 因为T1,T2,…,TN为C到E上的非自渐近拟非扩张映象,由上述定义可知,它们是C到E上的非自渐近拟非扩张型映象.由定理1的结论可知推论成立.
推论2 设E是一实Banach空间,C是E上非空闭凸子集且为E上的收缩核,P:E→C的保核收缩映象,T1,T2,…,TN为C到E上的非自渐近非扩张型映象,且是非空闭集.,i=1,2,…,N是C上的N个有界序列,,i=1,2,…,i=1,2,…,N,是[0,1]上的序列且满足:
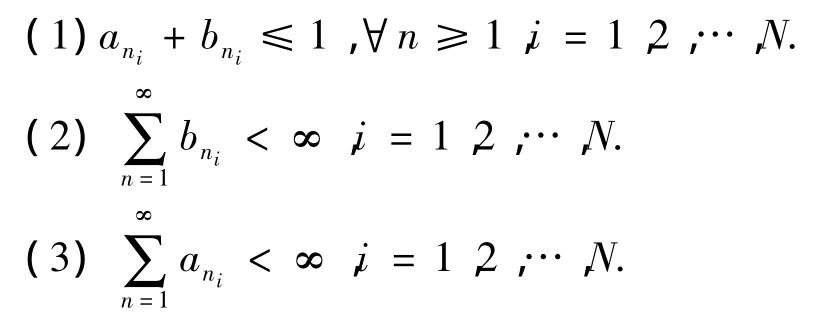
则(1)所定义的序列{xn}强收敛于T1,T2,…,TN的公共不动点的充分必要条件为:

证明 因为T1,T2,…,TN为C到E上的非自渐近非扩张映象,由上述定义可知,它们是C到E上的非自渐近拟非扩张型映象.由定理1的结论可知推论成立.
2 结束语
证明了具有误差的序列{xn}收敛于T1,T2,…,TN的公共不动点的充分必要条件为:)=0,其中T1,T2,…,TN为C到E上的非自渐近非扩张映象.
[1] Tian Y X,Chang S S,Huang J L.On the approximation problem of common fixed points for a finite-family of non-self asymptotically quasi-nonexpansive-typemappings in Banach spaces.Computers & Mathematics with Applications,2007,53:1847-1853.
[2] Moudafi A.Viscosity Approximation Methods for Fixed Points Problems[J].J Math Anal Appl,2000,241(1):46-55.
[3] 张石生.Banach空间中渐近非扩张映象不动点的迭代逼近题.应用数学学报,2001,24(2):236-241.
[4] 杨莉,张石生.渐近非扩张映象具误差的迭代序列的收敛性.数学的实践与认识,2006,36(12):261-268.
