催化剂颗粒撞击壁面的有限元分析*

刘冬玉，周迪峰

(浙江工业大学特种装备制造与先进加工技术教育部重点实验室，浙江杭州310032)

0 引 言

石油和化学工业是当代社会最基本、最大的三大支柱产业之一。催化剂在石油和化学工业发展中占据着举足轻重的地位。催化剂在整个催化裂化过程中都处于流化状态，通过气流的输送实现循环流动。正是由于这种循环流动，导致催化剂颗粒在整个催化裂化过程中，不断地撞击催化裂化装置的壁面，从而在碰撞过程中造成催化剂颗粒自身的变形或破碎。

为了减少由于催化剂颗粒撞击壁面所造成的催化剂颗粒的磨损，国内外学者已经进行了相关研究。其中，M·Junkar等［1］提出了运用有限元法模拟单颗粒撞击构件对构件造成的损坏;D·Griffin等［2］模拟了多个颗粒撞击壁面，研究了撞击后壁面的破损;计时鸣等［3］研究了单个磨粒撞击靶材后的表面残余应力。但在这些研究中，把催化剂颗粒简化成刚性，忽略了催化剂颗粒在碰撞过程中本身的变形和破碎，与工程实践中的结果有不少差距。

本研究对催化剂颗粒撞击壁面的过程建立有限元模型，针对催化裂化过程中的催化剂是脆性材料，采用相应的脆性裂纹材料模型。利用Abaqus进行建模和求解，模拟催化剂颗粒撞击壁面的过程。分析催化剂颗粒的撞击形态、入射速度和入射角度对催化剂颗粒磨损的影响，将对工程实践具有一定的指导意义。

1 脆性断裂理论

针对脆性材料，很多的脆性断裂是因为材料中的裂纹快速传播引起的，脆性材料的失效很多是突然断裂，没有明显的变形。Ashby［4］认为断裂成核裂纹长度和颗粒尺寸d成比例，断裂应力的表达式为:

式中:E—弹性模量，φ—冲击韧性。

如果材料的区服应力大于断裂应力σf，那么断裂在σy时发生;若σf＞σy，则裂纹在屈服应力σy开始，但不传播，直到达到σy时才能传播。

17世纪伽利略首次提出最大拉应力理论(第一强度理论)，它认为最大拉应力σ1是脆性断裂的主要元素，即只要最大拉应力σ1达到材料极限应力σu时，材料就会断裂破坏，脆性断裂的条件是:

第二强度理论认为无论在怎样的应力状态下，只要材料的最大应变ε1到达了材料的极限应变εu时，材料就会发生脆性断裂，脆性断裂的条件为:

Finnie［5］提出了磨损量的表达式为:

式中:k—作用在粒子上的竖直力分量和水平力分量的比值;c—冲击粒子的比值;φ—切削长度和深度的比值;σf—流动应力，Pa;v—速度，m/s;m—质量，kg;f(γ)—函数。

其表达式为:

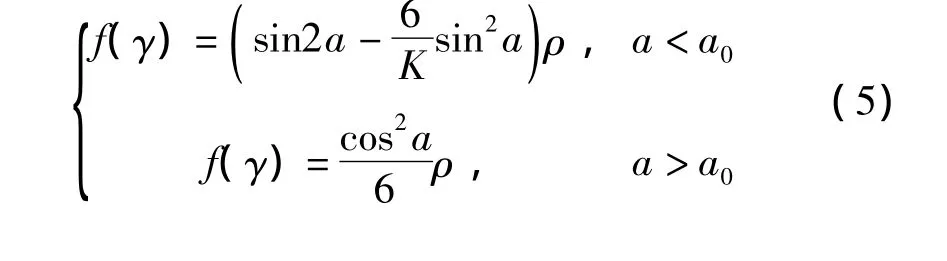
式中:a—颗粒撞击角度;a0—入射角度;ρ—密度，kg/m3。

2 有限元分析方法

在有限元中，用开裂模型来表征脆性材料的不连续的脆性行为。它只能对有限元模型的每个材料点独立计算，而不能跟踪单个的“宏观”裂纹。有限元中的开裂就是在某一点材料点探测到的裂纹开裂方向。开裂探测采用朗金准则(Rankine criterion)，其表达式为:

C=［CnnCttCssCntCnsCts］t，即最大主应力大于材料拉伸强度时，裂纹就会形成。只要搜索到裂纹，开裂方向就会被用于后继分析。在有限元中裂纹区的后继破坏行为用“拉伸硬化”来模拟，其有两种方式:后继破坏应力应变关系和断裂能开裂准则。后继破坏应力应变关系定义的是脆性材料开裂后的破坏特性，断裂能开裂准则是把单位裂纹张开面积需要的能量作为参数来反应裂纹的发展。

3 有限元模型的建立

本研究应用Abaqus仿真催化剂颗粒撞击壁面的过程，建立的催化剂颗粒撞击壁面的有限元模型如图1所示，由于研究的问题具有对称性，取1/2模型进行分析计算。壁面模型尺寸为50 mm×30 mm×20 mm.模型的单元选择八节点块状减缩积分单元(C3D8R)。为了减少计算时间，在碰撞区域把网格细化，碰撞区域的尺寸为:30 mm×15 mm×20 mm。催化剂颗粒的外径为8 mm，内径为2 mm，高为8 mm。

图1 有限单元的网格

壁面的材料高铝砖，材料参数如表1所示［6］。催化剂颗粒用圆环状的，其材料参数如表2所示［7］。

表1 高铝砖材料参数

表2 镍催化剂材料参数

4 有限元模型的有效性验证

为了验证模型的正确性，按文献［8］中的条件进行模拟计算，其模拟的是单颗玻璃颗粒撞击靶材，目标靶体的力学性能参数为密度7 930 kg/m3，弹性模量210 GPa。玻璃颗粒的力学性能参数为:密度2 500 kg/m3，弹性模量 7.92 Gpa，屈服应力1 060 MPa。玻璃颗粒的半径为0.05 mm;初始速度为300 m/s，摩擦因数为0.03，材料阻尼比0.05。本研究采用了其文选中相同的模型参数进行模拟，其模拟结果和文选中的结果如图2所示。从图2可看出两者的相符程度比较高，由此验证了本研究所采用的模型是正确的。

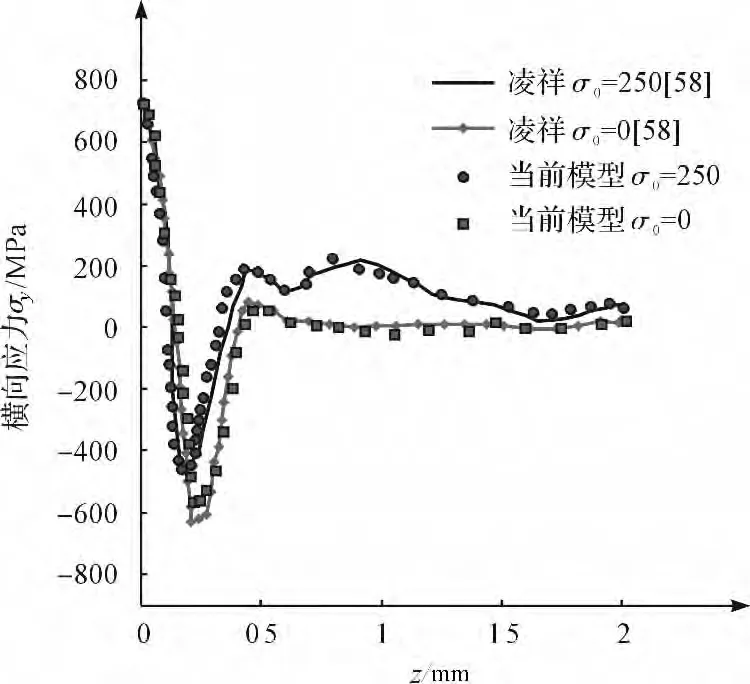
图2 靶材的残余应力

5 参数对壁面磨损量的影响

通过对单个催化剂颗粒撞击壁面的正确性验证，本研究将对催化剂颗粒撞击壁面的各个参数进行更深入的研究，从而可以系统地研究撞击过程中各个参数对催化剂磨损量的影响、催化剂磨损量的变化规律。

5.1 不同撞击形态对磨损量的影响

催化剂颗粒的撞击形态用方位角表示，即圆环催化剂颗粒的轴线和壁面表面的夹角。催化剂颗粒的撞击形态是影响磨损量的重要因素，为研究撞击形态对催化剂颗粒本身磨损的影响，本研究用5种不同撞击形态的催化剂颗粒竖直撞击壁面，绘制催化剂质量损失随方位角(撞击形态)的变化曲线如图3所示。

从图3可知，随着方位角度的增大，催化剂颗粒的质量损失先减小后增加，方位角太高或太低都会造成很大的质量损失，当催化剂颗粒以方位角为40°～50°的形态撞击时，质量损失最小。

图3 不同撞击形态的质量损失

5.2 不同入射速度对磨损量的影响

对于催化剂颗粒的磨损，入射速度是另一个重要的因素，选择45°的入射角以不同的入射速度得到的催化剂颗粒的磨损量如图4所示。

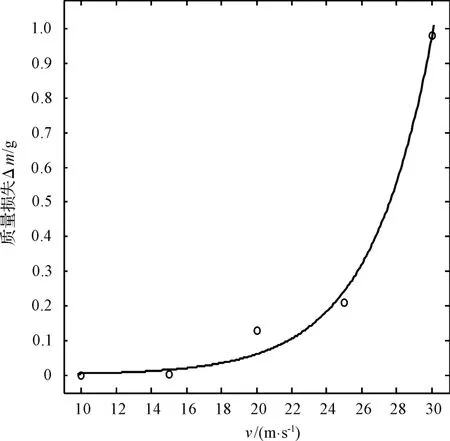
图4 不同速度的质量损失

从图4中可知，随着入射速度的增大，催化剂颗粒的磨损量也增大。当入射速度小于15 m/s时，几乎不会造成磨损，且在15 m/s～20 m/s磨损较小，之后随着速度的增加，磨损量迅速增大。这主要是因为在撞击过程中，速度的大小直接影响构件壁面受到的应力，而对于脆性材料，其失效方式为脆性断裂，当材料所受应力小于某一临界值时，材料处于弹性阶段，不会发生断裂，材料几乎没有质量损失，当材料所受到的应力大于某一临界值时，将会形成裂纹或者缺陷的扩展，导致材料迅速脆性断裂，材料的质量损失迅速增加。

5.3 不同入射角度对磨损量的影响

颗粒的入射轨迹和壁面表面的夹角，称为入射角。Bitter［9-10］定义了脆性材料的磨损率Wd公式为:

式中:M—质量，kg;γ—速度，m/s;a—入射角度;εb—磨损因子;γel—临界速度，m/s。

从式(7)中可以看出脆性材料的磨损率随着入射角度的增大而增大。为了研究入射角度对催化剂颗粒质量损失的影响，本研究选择入射速度为25 m/s的催化剂颗粒撞击壁面，绘制入射角度与催化剂颗粒质量损失间的关系如图5所示。

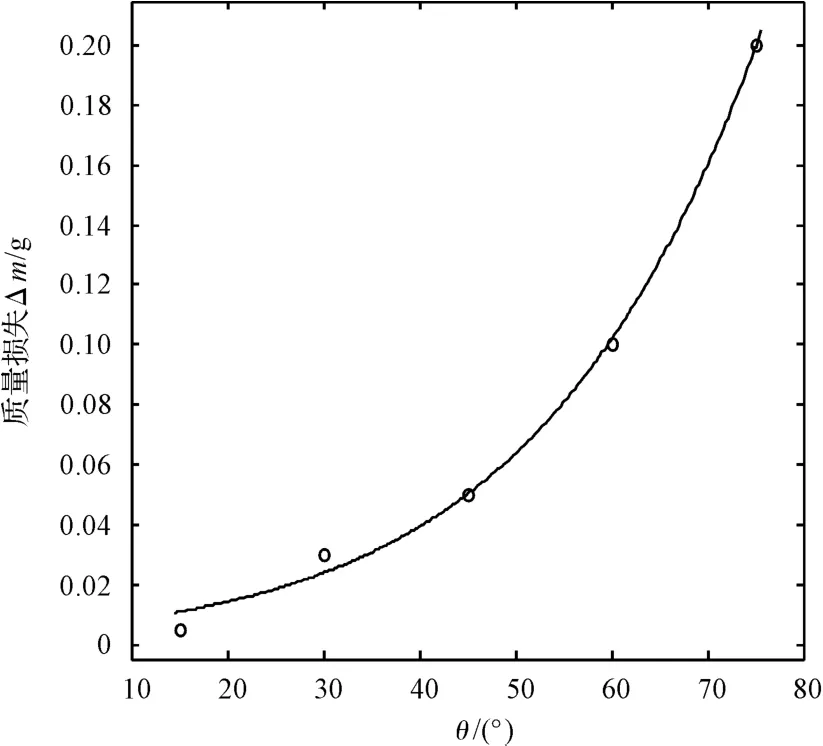
图5 不同角度的质量损失

从图5可知，随着入射角度的增大，催化剂颗粒的磨损量也跟着增大。这主要是因为角度越大，催化剂颗粒受到的法向撞击力就越大，从而磨损量就越大。当入射角度为75°时，催化剂颗粒的磨损量最大，这与Bitter所做的结果研究是一致的。

6 结束语

本研究应用有限元法对催化剂颗粒撞击构件壁面的过程进行了数值模拟，并且应用Abaqus软件建立了单颗催化剂颗粒撞击构件壁面的有限元模型，探讨了催化剂颗粒参数(撞击形态、入射速度、入射角度)对构件壁面造成的磨损量，整个模拟计算过程就像在实际构件壁面上做虚拟实验一样。笔者根据模拟结果，提出了优化装置的方案。

［1］JUNKAR M，JURISERVICE B，GRAH M.Finite element analysis of single particle impact in abrasive water jet machine［J］.International Journal of Impact Engineering，2006，32(7):1095-1112.

［2］GRIFFIN D，DAADBIN A，DATTA S.The development of a three-dimensional finite element model for solid particle element model for solid particle erosion on alumina［J］.Wear，2004，256(30):900-906.

［3］计时鸣，章 定，谭大鹏.磨粒流加工中单颗磨粒冲击的有限元分析［J］.农业工程学报，2012，28(S):68-73.

［4］CHRISTIAN J W，HAASEN P，MASSALSKI T B.Chalmers Anniversary Volume［M］.Pergamon Press，1981.

［5］FINNIE I.Erosion of surface by solid particles［J］.Wear，1960，3(2):87-103.

［6］孙加林，李福檠，彭西高.冲击参数对氧化铝基耐火材料常温耐磨性的影响［J］.耐火材料，2008，42(3):178-183.

［7］赵庆国，廖 晖，李绍芬.催化剂颗粒的力学性能与机械强度［J］.高校化学工程学报，2000，14(2):164-168.

［8］凌 祥，彭微微，倪红芳.喷丸三维残余应力场的有限元模拟［J］.机械工程学报，2006，42(8):182-189.

［9］BITTER J.A study of erosion phenomena，part Ⅰ［J］.Wear，1963，6(1):5-21.

［10］BITTER J.A study of erosion phenomena，partⅡ［J］.Wear，1963，6(3):169-190.