基于绕组函数的长定子直线同步电机建模研究*

包广清，梁铜川

(兰州理工大学电气工程与信息工程学院，甘肃兰州730050)

0 引 言

绕组函数法最先用于单相感应电机的计算机模拟，以及用于集中绕组的感应电机、双励磁磁阻电机和同步磁阻电机的分析。近年来，这种方法越来越广泛地应用于感应电机在不同故障下的瞬时动态分析，例如在气隙动态偏心的故障分析中。绕组函数法是从整体出发，不论电机气隙是否均匀，直接利用绕组的空间分布，写出绕组函数，结合气隙倒函数，求出电感参数[1]。

电感计算的准确性直接影响电机的数学模型，而电机的数学模型对电机的机械特性有很大的影响，因此研究者对直线同步电机进行仿真和计算时，必须建立合适的数学模型。本研究以绕组函数为基础建立长定子直线同步电机的数学模型，通过Matlab 求解电流微分方程，得到直线电机正常运行时的三相电流、电磁推力和励磁电流波形。

1 直线同步电机建模

1.1 绕组函数解析法

在长定子直线同步电机中，对A 相绕组，根据安培环路定律有[2]:

式中:H—A 相绕组磁场强度;J—电流密度;iA—A 相绕组电流;nA(x，x')—A 相绕组的绕组函数;x—从定子A相轴线算起的空间位移;x'—动子的位置。

又根据磁通连续定理:∮B d s=0，可以推导出A 相绕组磁势:

式中:B—绕组的磁感应强度，FA(x，x')—iA在A 相绕组中产生的磁势，MA(x，x')—修正的A 相绕组函数。

且:

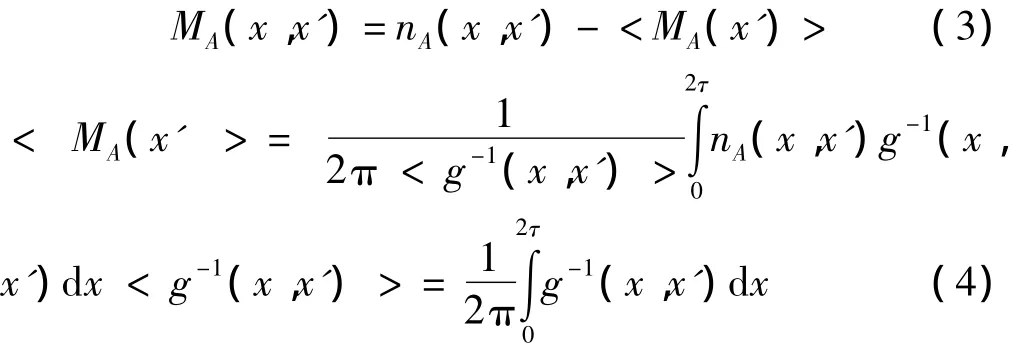
磁路的磁通φ为磁动势F 和磁导Λ的乘积:

式中:μ0—真空磁导率，S—磁路的截面积，L—磁路的长度。

对于长定子同步直线电机，忽略铁磁材料的饱和效应后，可近似认为直线电机中的磁势全部降落在气隙中，因而磁路的磁阻主要是气隙磁阻，由于同步电机中的气隙不均匀，致使气隙长度为动子位置的函数g(x，x')，g-1(x，x')为直线电机气隙倒函数。即:

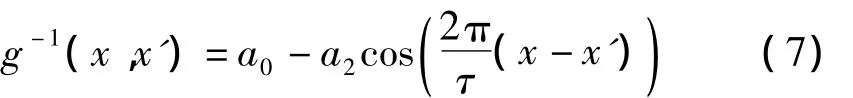
因此直线电机磁通的变化量为:

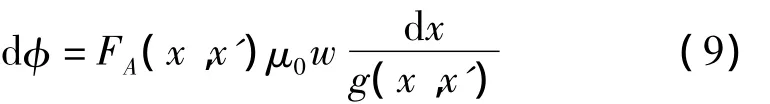
则 A、B 两相绕组的互感为[3]:

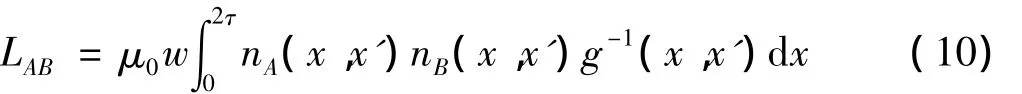
式中:nB(x，x')—直线电机B 相绕组随动子位置变化的绕组函数。

1.2 电机结构及数学模型

1.2.1 长定子直线同步电机结构

德国TR08 型磁浮列车的长定子直线电机截面结构如图1 所示。该电机采用长定子短磁极式，定子绕组为波绕组[4]。长定子铁芯连续铺设在轨道两侧下方，定子三相绕组嵌在铁芯槽内。励磁磁极装在车上，布置在车厢两侧，与定子绕组相对应，由车载直线发电机供给励磁电流。

图1 直线同步电机的纵向剖面图

1.2.2 数学模型

由于长定子同步直线电机的结构具有对称性，建立数学模型时只模拟一对磁级。理想化的直线同步电机的数学模型可以看作由三相定子绕组和一个励磁绕组构成。基于等效磁路法的直线同步电机电压方程如下:

定子回路电压方程:

动子回路电压方程:

磁链方程:

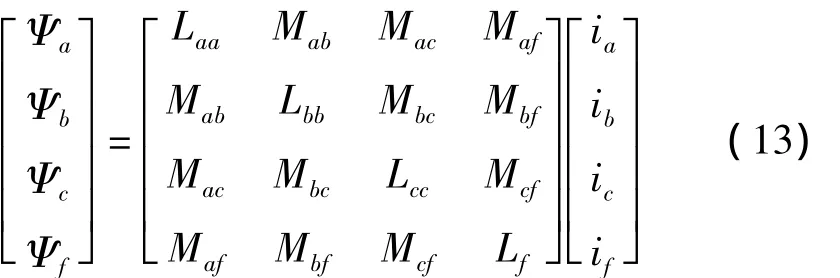
其紧凑写法为:

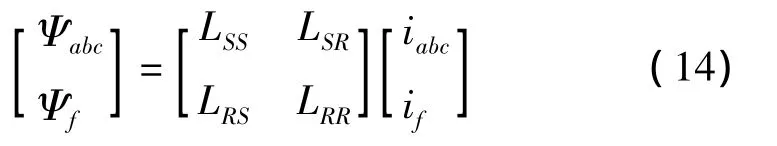
式中:r—定子绕组总电阻;rf—励磁绕组的电阻;Laa，Lbb，Lcc—各相定子绕组的自感;Mij(i=a，b，c，f;j=a，b，c，f;i≠j)—线圈的互感系数。

对于直线电机而言，根据以下公式对式(14)进行简化:

将式(11)和式(15)合并简化，得到长定子直线同步电机的数学模型公式，由此得到的数学模型为后续的仿真建立了基础。即:

1.3 电机参数的计算

由公式(10)可知，直线电机的电感与绕组函数和直线电机的气隙分布有关。根据文献[5]可知，直线电机的电枢绕组函数为:

式中:NS—电枢绕组的匝数。

1.3.1 定子绕组自感

定子绕组自感包含两个部分:恒值的绕组漏感Lls和气隙主磁通的电感Lms。本研究以a 相绕组为例，其自感值为:

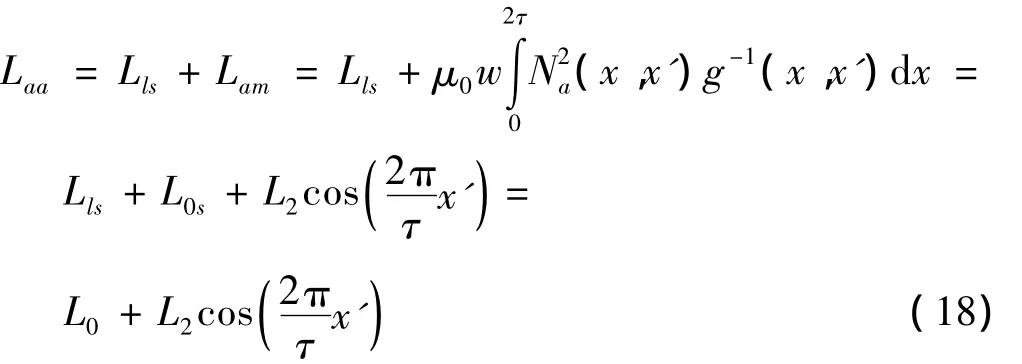
其中:

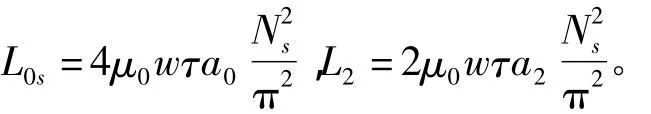
电枢部分的漏电感[6]主要由槽部漏感Ls、谐波漏感Lδ、端部漏感Le和齿端漏感Lt 组成，其相应的计算公式如下:

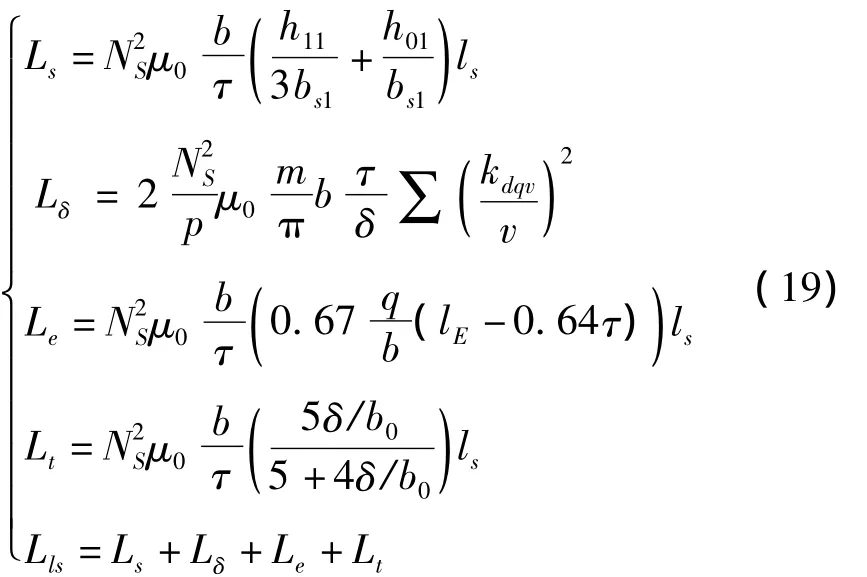
式中:τ—级距，b—定子铁芯宽度，h01—定子槽口高度，h11—线圈高度，bs1—槽口的宽度，ls—定子铁芯长度，p—极对数，m—相数，δ—气隙的有效高度，v—谐波次数，kdqv—定子v 次谐波绕组系数，lE—线圈的端部长度，q—每级的槽数，b0—齿槽的宽度。

同理可得b、c 两相绕组的自感如下:

1.3.2 定子绕组互感

定子三相绕组间的互感同理按照绕组函数公式计算，以b、c 相互感Mbc 为例，其计算公式如下:

同理可得其他两相的互感计算结果如下:

1.3.3 定子与动子绕组互感

直线同步电机简化模型中动子部分只包含励磁绕组，励磁绕组为集中绕组，基波绕组系数为1，定义动子励磁绕组函数为:

根据定子、动子绕组函数及气隙倒函数，推导出定、动子之间的互感如下:

式中:wfd—励磁绕组的匝数。

1.3.4 励磁绕组自感

励磁绕组的自感也分为两部分:恒值的漏感以及与端部漏磁自感:

式中:Lfd—跟气隙相关的自感。

且:

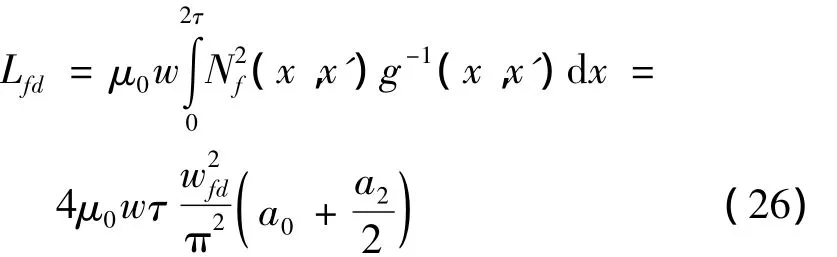
由文献[7]可知励磁绕组漏磁自感 Lfd1计算公式为:

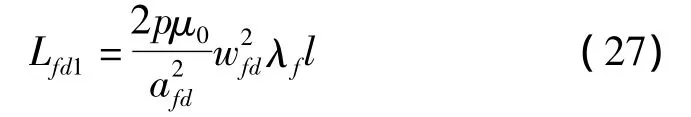
式中:λf—励磁绕组的比漏磁导，afd励磁绕组的并联数目，l—动子铁芯宽度。

从前面几个部分的计算可以看出，在直线同步电机的一对极模型电感参数中，定子绕组自感、互感和定子绕组与动子之间的互感都是动子位置变化的函数。由公式(25～27)可以得出励磁绕组的自感并不是随动子变化的量，而是一个常值。

1.3.5 电阻的计算

假设定、动子绕组的端部形状为半圆形，则定子绕组的每相电阻可以按照下面的公式进行计算[8]:

式中:p1—某段定子绕组的总极对数，ρ—工作温度下的导体电阻率，A—导体截面积，b—定子铁芯宽度。

1.3.6 电磁推力计算模块

直线同步电机的电磁推力是直线电机正常运行至关重要的性能参数之一，采用下面的公式计算[9]:

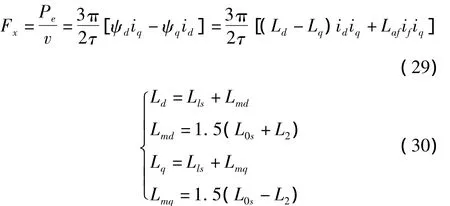
式中:Lmd，Lmq—直线电机直轴与交轴的主电感;ψd，ψq—直线电机直轴与交轴磁链;id，iq—定子侧直轴和交轴电流;Ld，Lq—直轴与交轴同步电感。

2 动态仿真

基于式(16)建立直线同步电机的仿真模型如图2所示。其中主要包括:电感矩阵模块、电感逆矩阵模块、电阻矩阵模块、电源矩阵模块、坐标变换模块、电磁推力计算模块。

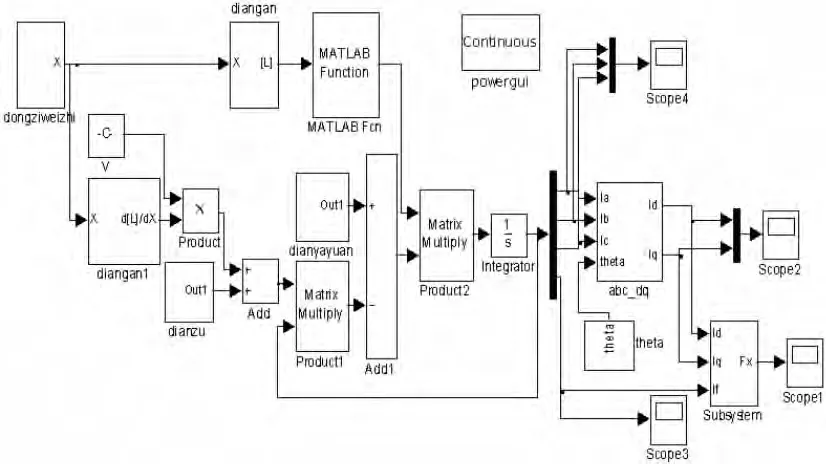
图2 动态仿真结构图

图2 中，动子的位置x=vt。电感矩阵、电阻矩阵和d[L]/d x 矩阵维数是4 ×4，并且是主对称矩阵。电源矩阵中，电压源的频率f=v/2τ，且矩阵维数是4 ×1。

3 电机参数及仿真结果

3.1 电机参数

以上海的悬浮列车运营线为基础，参照TR08 系列设计，其列车车体两侧各有一个直线同步电机共同产生电磁推力。该长定子直线同步电机的结构参数如表1 所示。

3.2 仿真结果

本研究将表1 中的参数输入到仿真模型中，定子侧绕组通入三相交流电，动子侧绕组加上直流电，三相电压和励磁电压的幅值取适当值，电源电压的频率通过动子速度求得，设定系统的仿真时间为0.04 s，其他仿真参数取默认值，即可得到直线同步电机在正常情况下的电流和电磁力波形。其仿真结果如图(3～7)所示。

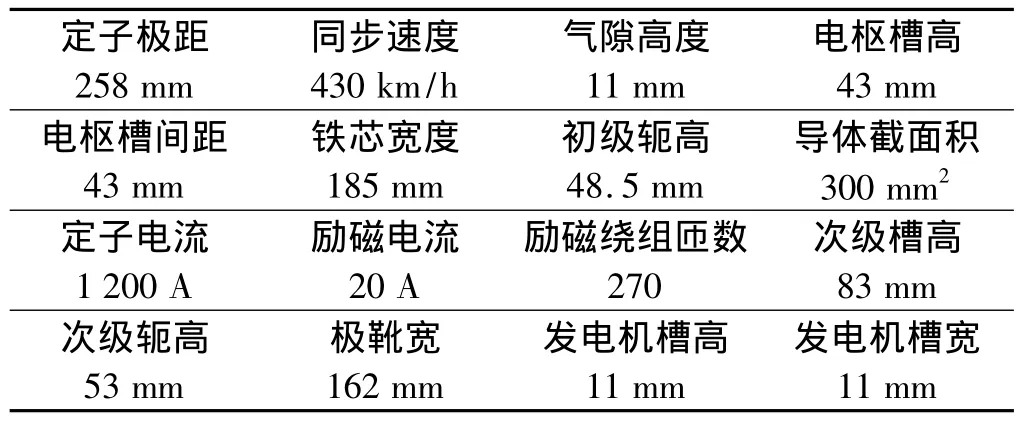
表1 长定子直线同步电机的参数

图3 定子a 相绕组自感

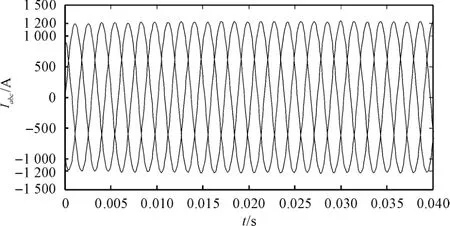
图4 三相定子电流

图5 d-q 轴电流

图6 励磁电流

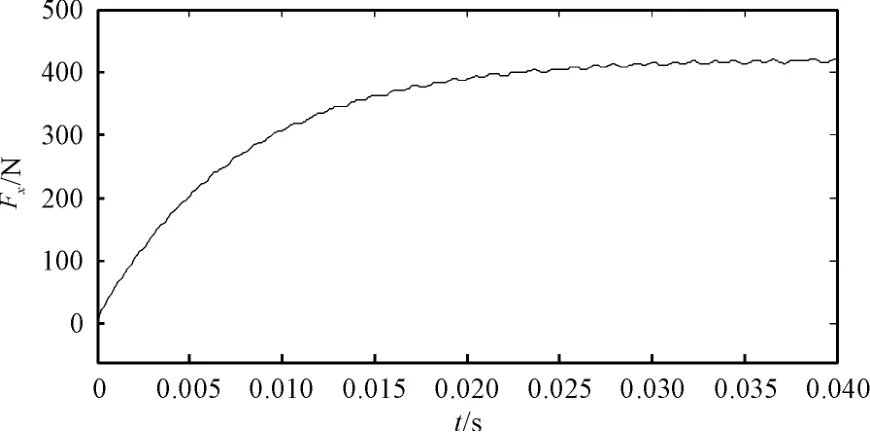
图7 电磁推力

由以上仿真结果得知:三相电流稳定后对称，互差120 °相角，励磁电流保持在20 A 左右，此时将三相电流作dq 分解，得到id=0，符合模型中设定的要求。

4 仿真与实验结果对比分析

为了验证解析法的准确性，本研究通过Ansoft 软件按照TR08 机械结构建立2D 有限元模型，将得到的电磁推力结果与解析法计算结果进行比较。

本研究依据表1 中直线同步电机的相关参数建立一对极模型[10]，以一对极为求解区域，定子绕组通入正弦电流，不考虑边端效应，取定子最大电流为1 200 A，励磁电流为20A，通过改变电枢电流的相位得到功角与电磁推力的关系曲线，电磁推力的计算采用麦克斯韦张量法。

在直线电机理论中，功角是指感应电压与外电压的夹角，又称功率角，功角对直线电机的推力和悬浮力有极大的影响。建立的单个电磁铁模型中，当其他条件都不变时，将动子的速度设置为0，定子侧通入三相对称电流，在Ansoft 后处理中纵坐标选择电磁推力，横坐标选择2 ×180 ×f ×time 角度变量(f 为电枢三相电流频率，time 为时间变量)。得到电磁推力随功角的变化曲线如图8 所示。

图8 推力随功率角的变化

由图8 可知，最大推力对应的功角为89.8128 °。由于改变定子电流初始相位可以体现出功角对电磁推力的作用，本研究将该功角分别代入到定子侧三相电流的相位中，动子的速度设置为430 km/h。得到单个电磁铁模型的最大推力波形如图9 所示。

图9 单个电磁铁推力波形

按照Matlab 计算结果，id=0 时，其功角为90 °，此时本研究采用Ansoft 麦克斯韦张量法的计算结果电磁推力为1 194.6 N/m(其中指的是铁芯的硅钢片厚度，需要乘以实际的铁芯宽度才为一对极下的电磁力)，将结果转换为沿气隙单位长度的结果。

每单位长度的电磁力Fx为:

通过与Matlab 数值计算的结果Fx=401.2 N/m比较发现，电磁推力的结果误差为6.31%，说明解析法计算的结果存在一定的误差。

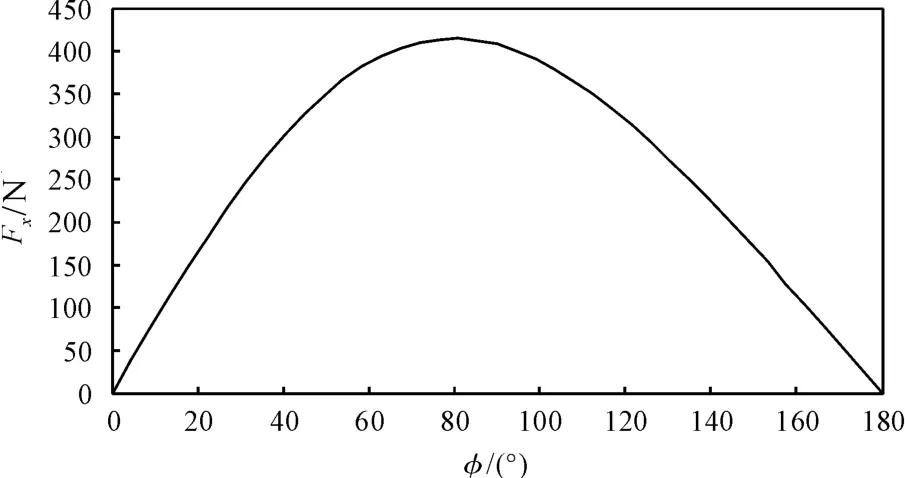
图10 解析法的电磁推力与功角关系

解析法的电磁推力与功角关系如图10 所示。

从图8 和图10 的计算结果比较可以发现，在Ansoft 计算中，当功角φ＜90 °时，电磁推力随着功角的增大而增大，φ＞90 °时，电磁推力随着功角的增大而减小，而在Matlab 计算中，功角φ的临界值符合Ansoft的计算结果，但是功角点对应的电磁推力比有限元计算的结果偏小，这是由于解析算法中的气隙函数的偏差造成的，但是可以证明解析法计算结果和Ansoft 有限元的计算结果总趋势是相同的。

5 结束语

直线同步电机的运行方式与普通旋转电机类似，本研究根据旋转电机的电压、磁链方程对其进行数学建模，并建立了电流的微分方程。

(1)针对数学模型中的部分参数如漏感、电阻等，可以沿用旋转电机的计算方法;而针对电感参数，则采用绕组函数法进行精确的推导计算。

(2)通过Simulink 建立电流微分方程的仿真模型，得到了三相电流、励磁电流和电磁推力的波形。

(3)最后将解析法得到的结果和有限元计算的结果进行了对比，证明了本研究方法的可靠性。

[1]叶云岳.直线电机原理与应用[M].北京:机械工业出版社，2000.

[2]AI-NUAIM N A，TOLIYATH A.A novelmethod formodeling dynamic air-gap eccentricity in synchro-nous machines based on modified winding function theory[J].IEEE Transactions on Energy Conversion，1998，13(2):156-162.

[3]于 芳，余海涛，胡敏强.长定子直线同步电机电磁推力计算和故障分析[J].微电机，2009，43(8):31-34.

[4]吴祥明.磁浮列车[M].上海:上海科学技术出版社，2003.

[5]于 芳.直线同步电机运行状态计算和故障仿真分析[D].南京:东南大学电气工程学院，2010.

[6]陈世坤.电机设计[M].北京:机械工业出版社，1983.

[7]高景德，王祥珩，李发海.交流电机及其系统的分析[M].北京:清华大学出版社，1993.

[8]卢琴芬，陈 宇，叶云岳，等.长定子直线同步电机的电抗计算与力的分析[J].中小型电机，2003，30(3):17-19.

[9]韩继文.不同磁场定向控制方式下高速磁悬浮列车牵引特性的分析[D].北京:中国科学院电工研究所，2006.

[10]李周清.基于Ansoft 的永磁同步电机建模与仿真[J].机电工程，2012，41(4):35-39.