基于DEM的软固结气压砂轮粘磨层劲度模量虚拟实验研究*

2014-09-15计时鸣蔡姚杰金明生张鹤腾蒋鑫鑫

机电工程 2014年3期

计时鸣，蔡姚杰，金明生，张鹤腾，蒋鑫鑫

(浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点实验室，浙江杭州310014)

0 引言

随着模具行业的不断发展，模具已经广泛地应用于各行各业，人们对模具质量的要求也越来越高。为了改善模具的使用性能，延长模具的使用寿命，模具表面激光强化处理技术逐渐成为了代表国际先进水平和未来发展方向的高效、绿色制造方法［1-2］。然而，模具表面激光强化给后续加工带来了难度，利用传统模具光整加工方法加工，加工效率极低。浙江工业大学计时鸣等人［3］研发了一种新型的光整加工工具—软固结磨粒气压砂轮。该工具能对激光强化后的模具表面进行高效地精密加工，可有效地解决激光强化后模具表面加工的问题。软固结磨粒气压砂轮加工方法借鉴于气囊抛光技术—由D.D.Walker等人［4］提出的应用于回转对称型光学曲面的新型抛光技术。目前，软固结磨粒气压砂轮光整加工方法存在的问题主要有气压砂轮自动化加工和质量优化。

在软固结气压砂轮光整加工的过程中，粘磨层与工件接触并产生形变，同时橡胶气囊也产生相应形变，要使气压砂轮具备良好性能及较长寿命，要求粘磨层劲度模量(应力与应变的比值)与橡胶气囊的弹性模量相近。对于粘磨层的应力与应变之间的关系，丁洁瑾等人［5］已经做了相关研究，但由于可变参数过多，如磨粒类型、磨粒粒度、粘结剂类型、磨粒与粘结剂比例、粘磨层厚度等，如此多的参数，要一一通过实验从而确定气压砂轮的最优制作参数显然是不切实际的。

本研究利用离散元方法(DEM)对软固结气压砂轮粘磨层进行仿真分析，从而优化软固结气压砂轮粘磨层的各类参数。

1 离散元方法

1.1 起源与发展

离散元方法(DEM)是20世纪70年代初由Cundall教授首先提出的［6］。后来，逐渐发展成为离散元软件PFC2D/3D，形成了较系统的模型与方法。我国离散元研究最初由王泳嘉引入，用于岩石力学和颗粒系统的模拟［7-8］。

近年来，离散元方法的应用领域又扩展到求解连续介质及连续介质向非连续介质转化的力学问题上。软固结气压砂轮光整加工工具由机械臂、固定基体、气囊固定环、橡胶气囊、粘磨层组成，粘磨层如图1所示，由磨粒和粘结剂均匀混合制成。建立在传统的连续介质力学基础上的有限元法等数值计算方法难以直接用于计算和模拟材料具体的破坏形式和破坏过程，而利用离散元方法仿真能更好地模拟损伤和破坏的过程［9］。

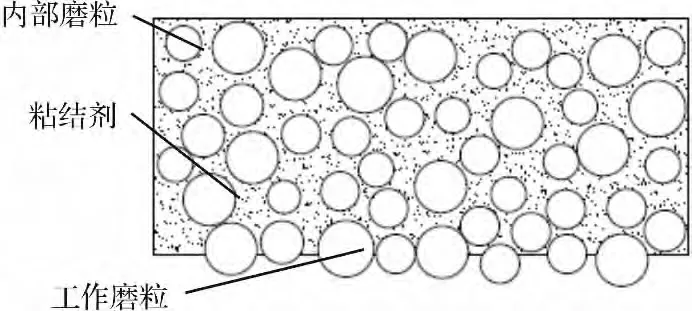
图1 粘磨层

1.2 离散元仿真软件

离散元仿真软件主要有 PFC2D/3D、UDEC、3DEC、GDEM等。这类软件常用的单元一般有块体单元和颗粒单元。离散单元本身为刚体，单元之间的相对位移等变形行为通过变形元件来实现，主要的变形元件有:弹簧、阻尼、摩擦元件等。本研究将以PFC为例做简单介绍。

与连续介质力学方法不同的是，PFC试图从微观结构角度研究介质的力学特性和行为。PFC研究的基本对象是颗粒和颗粒间的接触，它能直接模拟球形颗粒间的运动和相互作用的物理问题;可以通过“连接”两个或多个小颗粒来创建任意形状的大颗粒，“连接”而成的“颗粒集合体”可以作为独立的颗粒体研究。PFC可以模拟固体的破裂问题，通过“粘结”相邻颗粒得到的颗粒集合体可作为具有弹塑性的“固体”，当颗粒间的“粘结”逐渐破坏时，该固体即产生“破裂”。

2 软固结气压砂轮粘磨层特性

2.1 软固结气压砂轮

软固结磨粒气压砂轮作为一种柔性的加工工具，由基体、橡胶气囊、气囊固定环和粘磨层组成，其特点主要在于磨粒群在柔性支撑环境下针对高硬度表面进行加工。其柔性支撑主要体现在橡胶气囊和粘磨层的弹性，同时还受橡胶气囊内气压大小的影响。

橡胶气囊结构为空心半球形，主要作用是承担工作载荷和提供弹性支撑，使光整加工过程中具有仿形特性，因此，橡胶气囊必须具备良好的韧性、弹性、耐压缩、耐高温、抗老化等特性。

软固结气压砂轮的粘磨层是指一层包覆在橡胶气囊表面由磨粒和粘结组成的混合料。粘磨层直接与工件接触，通过磨粒与工件之间的相对运动起到切削效果，因此，粘磨层的特性对加工效果影响最直接。粘磨层中磨粒可选类型有金刚石磨粒、立方氮化硼磨粒、氧化铝磨粒、碳化硅磨粒等，磨粒粒径根据加工需要选择。粘结剂可以选用橡胶类粘结剂509、801、硅酮密封胶等。

2.2 粘磨层粘弹性本构模型

如果一物体在外力作用下既产生弹性变形又表现出粘性流动的性质，则该物体就是粘弹性体。软固结气压砂轮的粘磨层是典型的粘弹性体，在光整加工过程中表现出了粘弹性。粘磨层作为粘弹性体，其应力与应变本构关系不像胡克弹性体那样成正比例关系，而是呈非线性关系，且应变增大与回复两条曲线并不重合，这是粘弹性体重要的特征，即蠕变效应和应力松弛现象。具体地说，蠕变效应是指粘磨层在应力σ作用下产生应变ε，而该应变不仅与应力大小有关，还是关于时间t的函数，即:

式中:εσ—关于应力σ的函数，εt—关于时间t的函数。

也就是说，当粘磨层在一定应力作用下产生相应应变时，如保持应力大小不变，粘磨层的应变会随着时间的延长而增加。应力松弛现象是指粘磨层在应力作用下粘性应变分量随时间不断增长，使回弹应变分量随时间逐渐降低，从而导致变形恢复力随时间逐渐降低。

在分析粘弹性体的应力与应变本构关系时，不能像分析粘性体和弹性体一样简单地表达，必须用不同的元件进行组合才能进行分析。常用的本构模型有Voigt-Kelvin并联模型、Maxwell串联模型和Burgers模型。Voigt-Kelvin并联模型用于描述存在蠕变效应的力学行为，无法体现应力松弛现象;Maxwell串联模型用于描述存在应力松弛现象的力学行为，但无法体现蠕变效应;Burgers模型如图2所示，通过将前两种模型串联能同时描述存在蠕变效应和应力松弛现象的力学行为［10］。因此，Burgers模型可以作为软固结气压砂轮的粘磨层本构模型，其本构方程为:

图2 Burgers模型

其中:

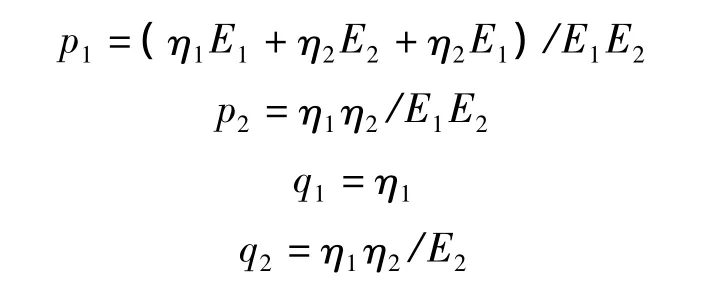
在研究粘磨层本构模型的过程中，本研究将应力与应变的比值定义为劲度模量，即:

粘磨层的劲度模量与橡胶材料的弹性磨量概念相似，由于粘磨层包覆在橡胶气囊上，应使橡胶气囊与粘磨层保持良好的接触，并在光整加工过程中保持良好的寿命，不至于脱落，本研究要求粘磨层的劲度模量与橡胶气囊的弹性模量相近。由于参数过多，通过实验测量粘磨层的劲度模量将十分繁琐，可使用离散元仿真软件PFC2D进行仿真分析。

2.3 粘磨层接触模型

在PFC2D中，基本单元体为圆形，粘磨层中每颗磨粒即可等效为一个圆形，粘磨层的本构特性将通过接触本构模型来模拟。由于粘磨层中磨粒并非均匀分布，也就是说磨粒与磨粒之间的接触力不尽相同，本研究将粘结剂等效为更小的圆形与磨粒混合随机分布，这样就要求定义粘结剂内部、粘结剂与磨粒、磨粒与磨粒的接触模型。

PFC2D中颗粒间的接触本构模型有:①接触刚度模型;②滑动模型;③连接模型，又分为接触连接模型和平行连接模型。接触连接模型中描述的连接只发生在接触点很小范围内，平行连接模型描述的连接发生在接触的颗粒之间圆形或方形有限范围内。接触连接模型中的接触连接只能传递力，而平行连接模型中的连接可以传递力和力矩。仿真时笔者选择线性接触刚度模型作为磨粒与粘结剂接触模型，选择接触连接模型作为磨粒与磨粒接触模型，选择平行连接模型作为粘结剂内部接触模型。

线性接触刚度模型中对接触的颗粒进行分析时，将接触的颗粒假象成一端点在颗粒中心的弹性梁，梁受到力或力矩作用时就相当于作用于颗粒中心。该模型由以下特征参数描述:①几何参数，包括:长度、断面积、惯性矩;②变形参数，包括:杨氏模量、泊松比;③强度参数，包括:法向强度、切向强度。

接触连接模型是散体特有的连接形式，颗粒间的作用力是接触面上的接触力，力—位移行为由3个参数描述，分别是:法向刚度kn、切向刚度ks、颗粒间摩擦系数μ，不存在变形协调条件的约束，颗粒排列往往是无序的，而且颗粒尺寸、形状、材料都可以不同。接触型连接形式是离散元方法的基础和发源地，适用于分析散体的力学行为。

平行连结模型主要用来处理连续介质问题，颗粒间的作用力由键来模拟。其胶结键的力—位移行为由5个参数描述，分别是:单位面积上的法向刚度、单位面积上的切向刚度、抗拉强度、抗压强度、键的半径倍数。两种类型的接触可以同时存在，直到超过接触强度。

3 粘磨层劲度模量仿真与实验测量

3.1 模型建立

在软固结气压砂轮光整加工过程中，粘磨层在一定压力下与工件接触，由于橡胶气囊和粘磨层的仿形能力，粘磨层该部分与工件表面贴合，呈现被加工面的形状。软固结气压砂轮加工的工件多数为磨具平面或大曲率曲面，因此，利用PFC2D建模时可以将粘磨层视为矩形。

首先，本研究用WALL命令建立矩形区域，然后利用GENERATE命令生成颗粒体，同时，指定颗粒半径上、下限，并使其服从高斯分布，最终颗粒的半径利用PFC2D的内置函数语言确定。其中，存在一个关键问题—如何让颗粒流填满矩形区域。当磨粒与粘结剂类型、比例确定后，若直接计算出总体积，直接生成目标颗粒数目，程序运行结果往往会溢出，因此，可以通过先生成比目标半径稍小的圆形颗粒，再设置一个半径放大倍数，将颗粒放大，使其通过自动调整慢慢填充整个区域。

在此引入孔隙率的概念，孔隙率定义为矩形内孔隙面积与矩形面积之比:

式中:Ap—矩形区域内所有颗粒的总面积，A—矩形的总面积。

则有:

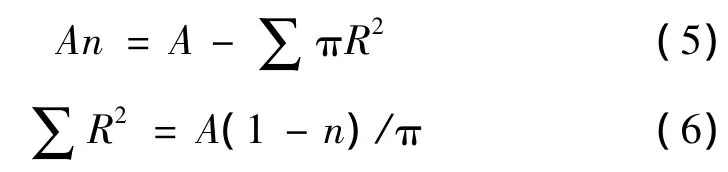
初始孔隙率定义为n0，目标孔隙率为n，则:

目标半径和初始半径的比值称为半径放大倍数，记为m，则:

选定目标孔隙率n0、放大倍数m、目标半径R，则可求得初始半径R0，生成一个包含圆形颗粒的矩形空间，该矩形空间如图3(a)所示。图3中，显然矩形空间未被填满，然后将原有圆形颗粒半径扩大m倍，粘磨层模型如图3(b)所示。

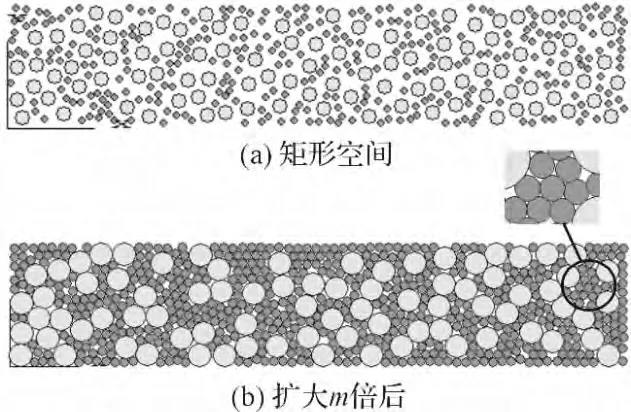
图3 粘磨层模型

3.2 材料特性及接触模型参数设置

在对软固结气压砂轮粘磨层进行仿真分析的过程中，本研究选用最常用的磨粒材料碳化硅为例，粘结剂则选用酸性硅酮密封胶，碳化硅磨粒与硅酮密封胶质量比为4∶1。

已知碳化硅的弹性模量为420 GPa～450 GPa，泊松比为 0.17，体积模量为 220 GPa，密度为 3.21 g/cm3。酸性硅酮密封胶性质如表1所示。

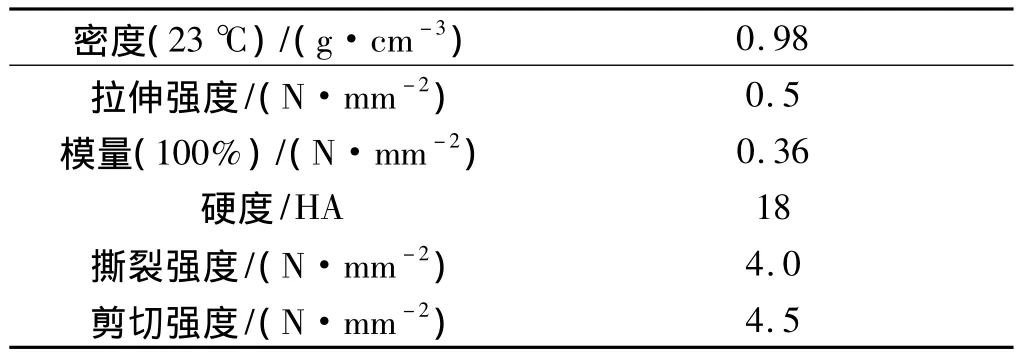
表1 德国瓦克酸性硅酮密封胶性能

粘磨层模型中碳化硅颗粒用半径为RA的圆形颗粒模拟，粘结剂颗粒半径为RB，则在线性接触刚度模型中梁的半径为:

梁的长度为:

断面积为:

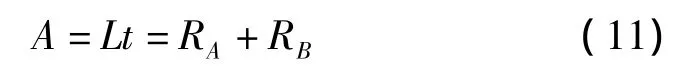
式中:t—假象颗粒圆盘厚度，取t=1。

惯性矩为:

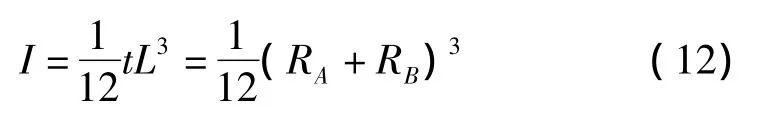
对于碳化硅颗粒，其法向刚度为:

而:

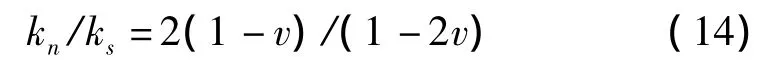
则其切向刚度为:

同理可得粘结剂颗粒的法向刚度和切向刚度，而线性接触中假象接触的颗粒为串联，其接触刚度为［11］:

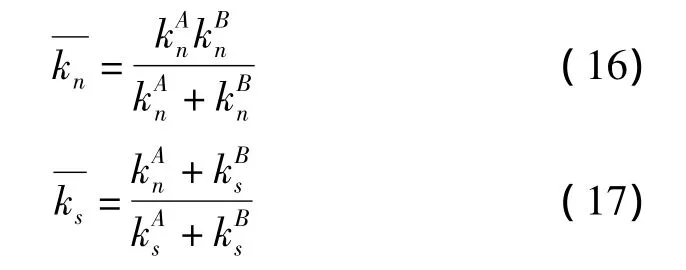
粘结剂内部的接触模型选用平行连接模型，由于该模型中参数较多，PFC2D中一般利用数值实验模拟，拟合材料宏观特性，从而得到详细的微观参数值。首先建立粘结剂模型，提取两端与矩形两边相接触的颗粒，分为左、右两个颗粒群，再分别给这两个颗粒群施加固定速度，速度方向分别为x轴正、负方向，模拟对模型进行拉伸试验，直至模型平行连接键断裂。在拉伸过程中，记录模型中平均接触应力，再转换为拉伸应力，输出应力曲线如图4所示。根据参数设置的不同分为3组(实际仿真为数十组)参数，各组参数设置pb_kn(法向刚度)、pb_ks(切向刚度)、pb_nstren(法向连接刚度)、pb_sstren(切向连接刚度)、pb_rad(连接区域半径)分别为第 1 组:5.7 ×1012、2.7 ×1022、8.3×108、4.3 ×108、0.5;第 2 组:5.7 × 1022、2.7 × 1012、2.3×109、1.3 × 109、0.5;第 3 组:5.7 × 1013、2.7 × 1013、8.3 ×108、4.3 ×108、0.5。粘结剂(酸性硅酮密封胶)的拉伸强度为0.5 MPa，拉伸强度计算公式如下:

式中:b—模型宽度，mm;d—模型厚度，mm;Fmax—最大拉伸应力。

根据模型参数，可得最大拉伸应力为:

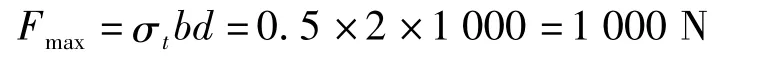
则由图4可知:第2组参数设置的模型拉伸应力峰值与粘结剂最大拉伸应力相当，可选用此时模型所用微观参数对粘结剂进行仿真分析。

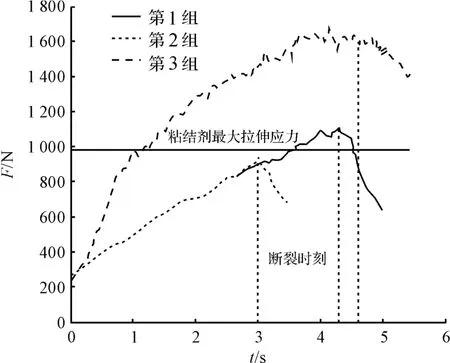
图4 应力曲线

3.3 粘磨层劲度系数仿真分析与实验

FISHTANK语言是内嵌于PFC2D的程序设计语言，它的作用是减少用户编程的工作量，将一些常用的实验程序直接提供给用户，用户只需改动相应参数就可以得到相应实验数据。其中双轴实验就是典型的例子。双轴实验的模型采用了通用的矩形模型，用户可以根据需要进行自定义。因此，可以通过FISHTANK中的双轴实验进行仿真分析。

粘磨层通过双轴实验得到应力与应变曲线如图5所示，则可得其劲度模量为2.22 MPa，为验证仿真分析是否准确，本研究将利用Instron拉力试验机对粘磨层进行拉伸实验。

图5 双轴数值实验结果

根据国标GB/T528-2009硫化橡胶或热塑性橡胶拉伸应力应变性能的测定标准，根据仿真分析建模时选用的磨粒粒径、磨粒种类、粘结剂和磨粒比例，本研究将粘磨层实验试样制成哑铃状，试样宽度为25 mm，有效拉伸长度为25 mm，相同成分的粘磨层试样制备3件，进行实验测量弹性模量取其均值。Instron拉力机可对粘磨层试样进行匀速单轴拉伸实验，从而获得粘磨层相关力学性能参数。

拉伸实验具体实验条件为:温度25℃，试样固化时间24 h，拉伸速度为1 000 mm/min。实验结果表明，当粘磨层成分为50%的36目碳化硅磨粒和50%的粘结剂时，其劲度模量均值为2.45 MPa，与仿真结果相对误差为: