雷电冲击试验冲击电压发生器调波电阻的确定

宣耀伟，乐彦杰，张娜飞，卢志飞

(国网浙江省电力公司舟山供电公司，浙江 舟山 316000)

0 引 言

电力系统的高压电气设备不可避免地会遭受雷电冲击，因此在型式试验或出厂试验时需利用冲击电压发生器进行雷电冲击试验[1-2]。IEC 60060-1[3]对标准的雷电冲击波形作了如下规定:波前时间tf为1.2 μs，半峰值时间 tt为50 μs，容许偏差分别为 ±30%和±20%。然而，在实际的雷电冲击试验中，往往不易直接得到标准的冲击波形，这要求试验人员具有丰富的试验经验，能够根据被试品的电压等级、容量正确调节设备参数，尽量减少试验次数，以减少对被试品的损害[4]。

文献[5]在Pspice环境下搭建了6级冲击电压发生器Marx回路，并研究调波电阻的变化对波形参数的影响。文献[6]在Pspice环境下对冲击电压发生器等值放电回路进行仿真，研究改变冲击电容、负荷电容、调波电阻对冲击效率、波前时间、半峰值时间的影响，最终用实验加以验证。文献[7]对7200 kV/480 kJ冲击电压发生器的标准雷电冲击电压、标准操作冲击电压的输出特性进行了试验研究，重点对雷电波放电等值回路和操作波等值回路进行了数学分析，并分别给出了雷电波、操作波调波电阻的计算方法。

基于以上文献，本研究对雷电冲击放电等值回路进行数学分析，建立关于波前电阻、半峰值电阻的非线性方程组，采用文献[8]提出的混合遗传算法进行求解。得到调波电阻的数值解后，进行仿真分析和现场试验验证。研究结果表明，雷电冲击波形的波前时间、半峰值时间均符合IEC标准要求，本研究所采用的调波电阻确定方法是有效的。

1 雷电冲击放电等值回路分析

放电等值回路如图1所示。主电容C1经由直流充电，当电压达到设定值U0时放电球隙击穿，放电一瞬间试品两端的电压波形即为雷电冲击波形。

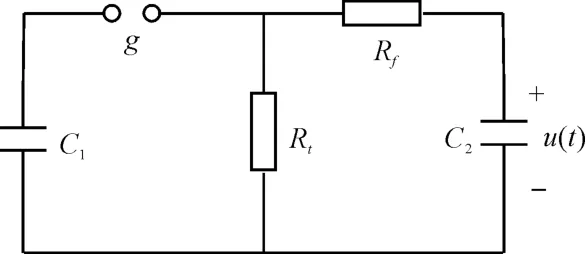
图1 放电等值回路

对等值回路建立微分方程:

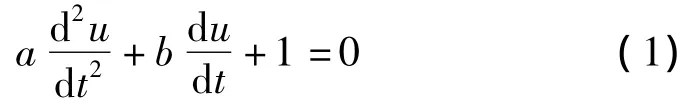
其中:a=C1C2RfRt，b=C1Rt+C2(Rf+Rt)。

C1的初始电压为U0，C2的初始电压为0，因此式(1)微分方程应满足如下初始条件:

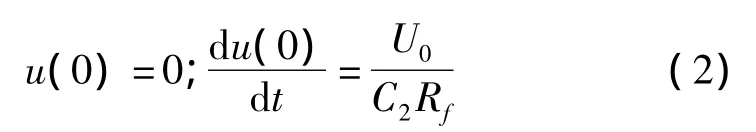
求解微分方程，可得冲击波形的时域表达式为:

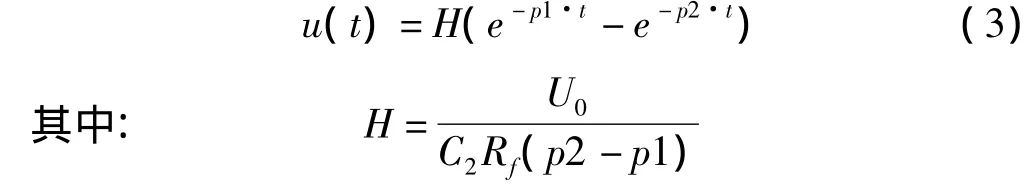
式中:－p1，－p2—特征方程ap2+bp+1=0的两个特征根。

－p1、－p2满足如下关系式:

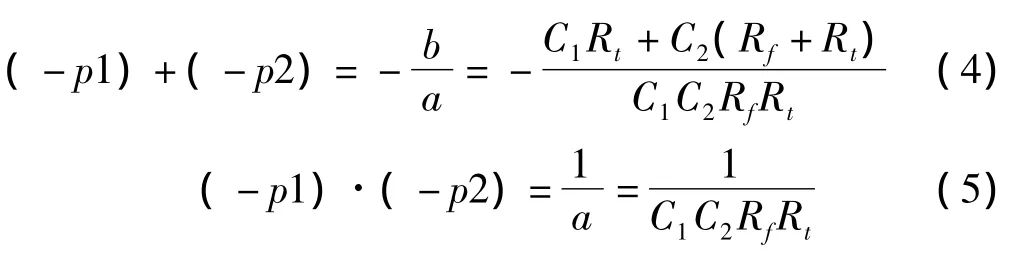
假定在tm时刻，u(t)取得最大值um，则tm处的一次导为0，即:

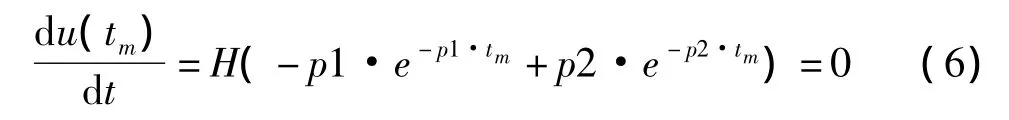
冲击效率为波形最大值与主电容C1初始电压之比，即:

雷电冲击波形由波前时间(tf)、半峰值时间(tt)描述，其定义如图2所示。

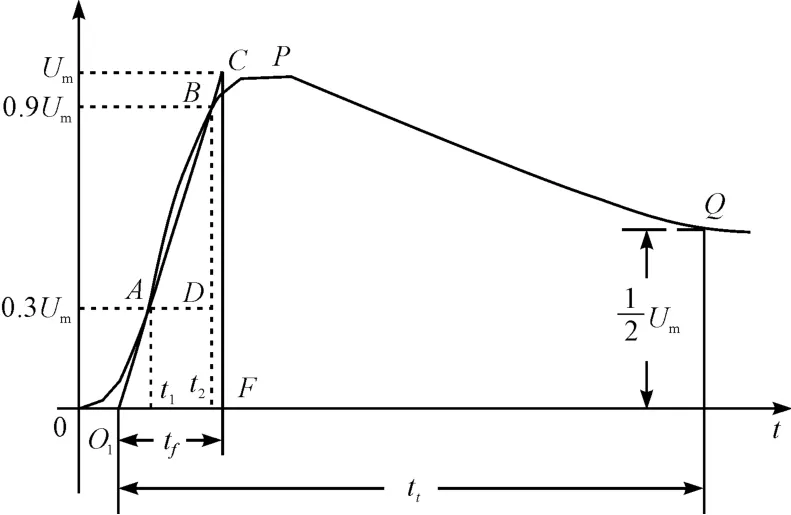
图2 雷电冲击波形的定义

30%、90%和50%峰值处对应的时间分别记为t1、t2和t50，如图2中的A、B、Q点所示。视在原点O1对应的时间记为tO1，其计算公式为:

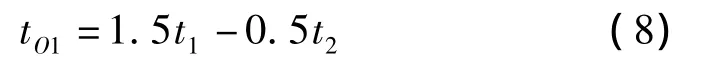
根据标准定义，tf和tt可由式(9，10)计算:

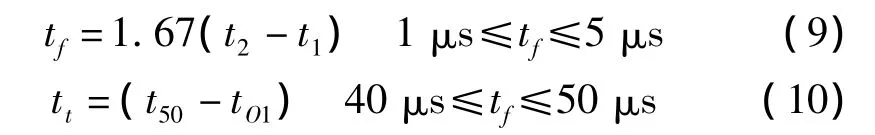
根据图2对雷电冲击波的定义，t=t50时，电压大小为峰值的50%，所以:

由式(4，5，6，8，9，10，12，13，14)可建立如下非线性方程组:

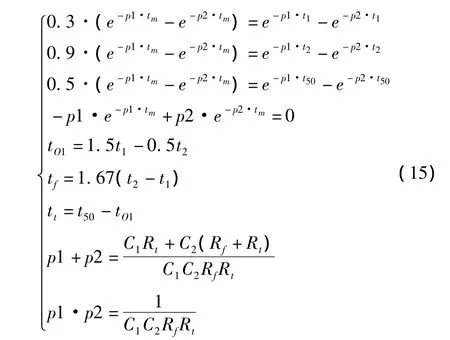
式中:C1，C2—已知的设备参数;tf，tt—设为 1.2 μs 和50 μs，因此方程组有 9 个方程，9 个未知量(p1，p2，tm，t1，t50，t2，tO1，Rt，Rf)，故可以求解。

2 仿真分析和现场试验验证

2.1 冲击电压发生器系统介绍

现场冲击试验采用北京华天机电研究所生产的CDYH-2400 kV/480 kJ冲击电压发生器成套试验设备，该设备由冲击电压发生器本体、3000 kV弱阻尼电容分压器、计算机测量与控制(光纤)系统组成，冲击电压发生器本体和电容分压器如图3所示。计算机测量与控制(光纤)系统通过PLC控制本体的充电，并将放电瞬间的电压波形记录至计算机中。冲击电压发生器本体采用双边对称式充电的Marx回路，总共12级，如图4所示。试验变压器T和高压硅堆D组成整流电路，经过保护电阻RB和充电电阻RC对各级的主电容器C进行充电，当充电至计算机设定的电压时，各级球隙击穿，致使各级电容串联放电产生冲击电压波形。rf、rt分别为每一级的波前电阻和半峰值电阻，多级冲击电压发生器的参数与等值回路参数有如下关系:Rt= ∑rt，Rf= ∑rf，C1=C/12。

图3 冲击电压发生器本体和电容分压器

冲击电压发生器各级电容量C为2 μF，总共12级，因此主电容量为 C1=C/12=0.1667 μF。

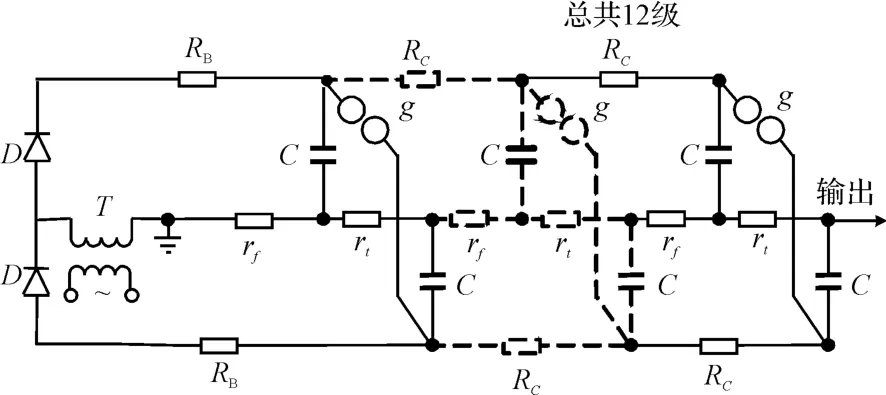
图4 双边对称式充电的Marx回路

电容分压器电容为400 pF，本体对地杂散电容约为300 pF，因此不接试品时负荷电容 C2按700 pF考虑。

2.2 混合遗传算法求解电阻参数

牛顿迭代法及其改进形式[9]是目前应用最广泛的非线性方程组求解算法，然而该类算法的收敛性依赖于初始值的选取，无法保证全局收敛，这给工程人员确定实际参数带来极大的困扰。遗传算法[10-11]具有较强的群体搜索能力和全局收敛性，然而在收敛速度和求解精度方面不如经典算法。因此，本研究采用文献[8]提出的混合遗传算法对式(15)所示的非线性方程组进行求解，结合遗传算法和拟牛顿法，既保证了全局收敛性和群体搜索能力，又保证较高的收敛速度和求解精度。

混合遗传算法引入了自适应概率pn，pn随着进化的增加而变大，最后于趋于常数，如下式所示:

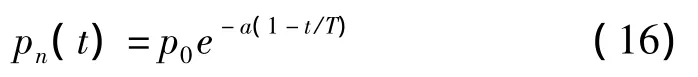
式中:T—遗传算法中设置的最大代数;t—当前代数;p0—局部搜索算子对每个个体的最大可能作用程度，该值越大则局部开采越充分，但同时会增加计算成本;a—控制算子概率变化的参数。

算法的基本流程如下所示。

Begin

确定设计变量上下限，随机产生父代群体，设定算法基本参数。

While

评价群体:计算各个个体的基本属性

依据交叉概率pc对群体进行算术交叉操作

依据变异概率pm对群体进行确定性随机方向变异操作

依据自适应混合算子概率pn对群体进行经典算法局部搜索

依据最优保留策略的联赛竞争算子选择新的群体

Until 进化到最大代数或者误差小于10－6

End

算法的参数选择如表1所示。

表1 混合遗传算法的参数选择

为了使获得的解满足物理意义的约束，需对部分变量的区间做限制。由于半峰值时间为40 μs～60 μs，波前时间为1 μs～5 μs，p1、p2 的区间分别设为[0，0.1]和[1，10]。Rt、Rf不可能为负值，均设成[0，∞]。最终求得的解为:(0.013785，2.495981，2.094458，0.138209，52.778927，0.856772，－0.221073，433.338932，574.765403)T，因此，波前电阻和半峰值电阻的理论计算值分别为:

Rt=433.338932 Ω，Rf=574.765403 Ω。

而设备的调波电阻仅有 25 Ω、72 Ω、120 Ω、150 Ω这4种，且电阻只能并联。为使实际电阻尽量接近计算值，最终确定:

各级的半峰值电阻为4个150 Ω并联，因此实际总的半峰值电阻设为:

Rt=12·(150/4)=450 Ω。

前6级的波前电阻为2个120 Ω并联，后6级的波前电阻为2个72 Ω并联，因此实际总的波前电阻设为:

Rf=6·(120/2)+6·(72/2)=576 Ω。

2.3 仿真分析

本研究在Matlab环境下搭建放电等值回路进行仿真，验证仿真波形的tf、tt是否符合设定值。然后，分别改变 Rf、Rt，观察仿真波形的变化，讨论 Rf、Rt的大小对 tf、tt的影响。

C1的初始电压设成1440 kV，Rf、Rt分别设成576 Ω、450 Ω时的仿真波形如图5、图6所示，此时波前时间 tf为1.199 μs，半峰值时间 tt为54.95 μs，符合1.2 μs(±30%)/50 μs(±20%)标准要求。

Rt保持不变，不同Rf下的仿真波形如图5所示。

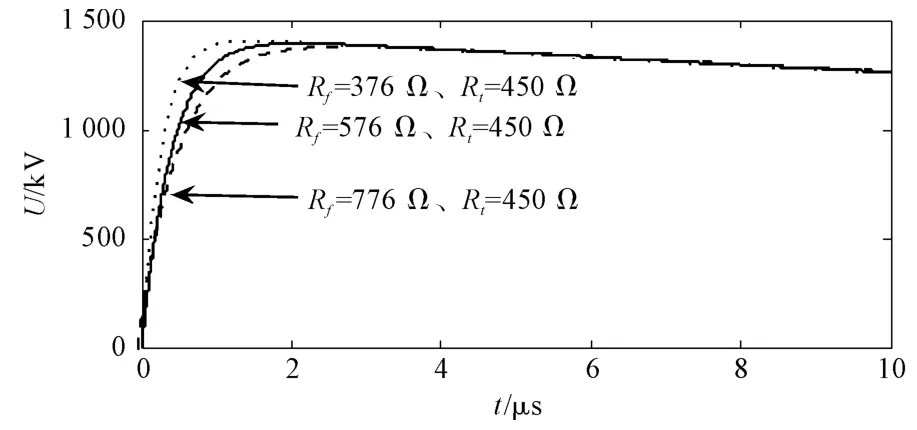
图5 Rt保持不变，不同Rf下的雷电冲击仿真波形

波前时间tf、半峰值时间tt和冲击效率η的变化如表2所示。

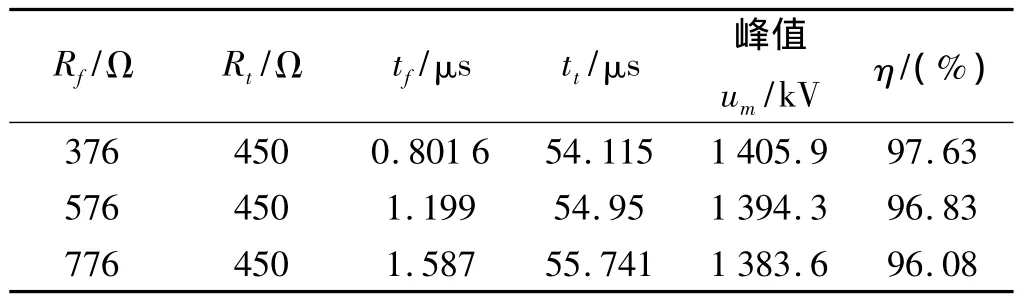
表2 Rt保持不变，不同Rf下的雷电冲击波形参数

由图5、表2表明，波形上升部分的快慢与Rf有关，Rf越大，则波前时间越大;同时也会影响冲击效率变化，Rf越大，则冲击效率越小。

Rf保持不变，不同Rt下的仿真波形如图6所示。

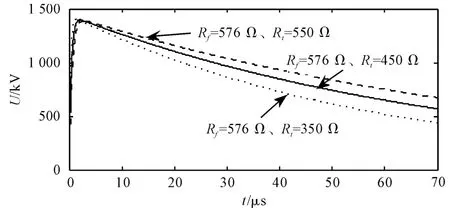
图6 Rf保持不变，不同Rt下的雷电冲击仿真波形

波前时间tf、半峰值时间tt和冲击效率η的变化如表3所示。

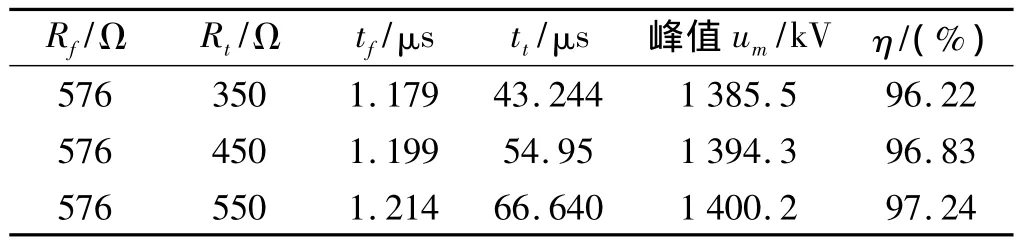
表3 Rf保持不变，不同Rt下的雷电冲击波形参数

图6、表3表明，波形下降部分的快慢与Rt有关，Rt越大，则半峰值时间越大。

2.4 现场试验验证

本研究进行现场雷电冲击试验时，波前电阻、半峰值电阻分别设成576 Ω、450 Ω，每一级的充电电压设成120 kV，则总充电电压值为1440 kV，冲击波形如图7所示。

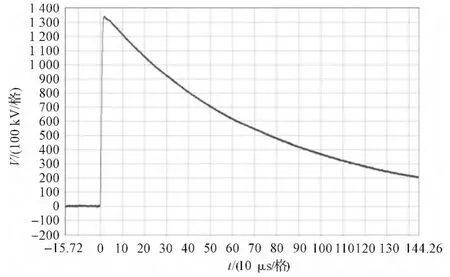
图7 现场雷电冲击试验波形

本研究连续进行3次雷电冲击试验，各次的波前时间、半峰值时间和冲击效率如表4所示。

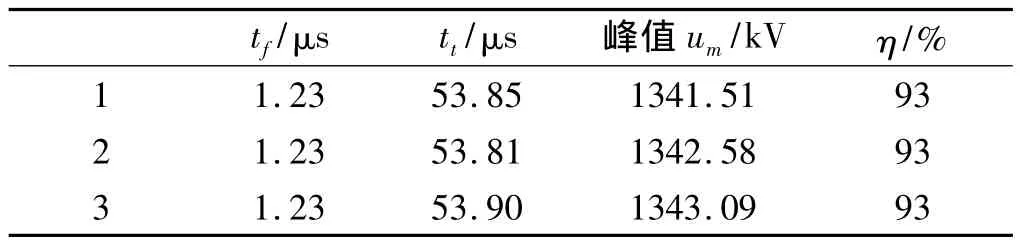
表4 连续3次现场雷电冲击试验的波形参数

由图7、表4可知，现场试验冲击电压波形的波前时间为1.2 μs左右，半峰值时间为 53 μs 左右，冲击效率为93%左右。由于现场试验中存在回路电感和充电电阻，且杂散电容的估计值与实际值有一定的偏差，现场试验波形与仿真波形有一定的差异，但大体上相近。

3 结束语

对于任意标准雷电波形，研究者只需将变量tf、tt设成试验要求的参数，采用混合遗传算法对非线性方程进行求解以确定调波电阻的大小。仿真和现场试验结果表明，本研究给出的调波电阻确定方法能够保证波前时间、半峰值时间均符合标准要求，方便现场试验人员快速确定电阻参数，缩短设备调试时间，减少对试品的损害。

实际试验中发现，当试品为大电容负载(可达3000 pF～10000 pF)时，试验回路中存在的电感对波形的影响不可忽略，调波电阻选择不当将会产生振荡和过冲，此时的放电等值回路应作为三阶电路进行分析。因此，试品为大电容负载时如何确定调波电阻将是下一步的研究工作。

[1]司文荣，傅晨钊，黄 华，等.雷电冲击电压波形K因子零相位数字滤波器设计[J].电工电能新技术，2012，31(2):11-14.

[2]王浩洋，孙 伟，傅正财，等.负荷对冲击电压发生器输出能力的影响研究[J].高压电器，2009，45(5):92-95.

[3]Internation Electrotechnical Commission.IEC 60060-1-2010.High-voltage test technique-Part 1:General definition and test requirement[S].Internation Electrotechinal Commission，2010.

[4]王淑红.变压器冲击电压波形参数的仿真研究[D].成都:华南理工大学电气工程学院，2006.

[5]VAHIDI B.Using pspice in teaching impulse voltage testing of power transforms to senior underduate students[J].IEEE Transactions on Education，2005，48(2):307-312.

[6]BASAR M F M，JAMALUDDIN M H，ZAINUDDIN H.Design and Development of A Small Scale System for Harvesting the Lightning Stroke Using the Impulse Voltage Generator at HV Lab，UTem[C]//Computer and Automation Engineering.Singapore:[s.n.]，2010:161-165.

[7]李广泛，廖蔚明，李庆峰，等.7200 kV/480 kJ冲击电压发生器的输出电压特性[J].中国电机工程学报，2008，28(25):1-7.

[8]罗亚中，袁瑞才，唐国金.求解非线性方程组的混合遗传算法[J].计算力学学报，2005，22(1):109-114.

[9]钱 春.基于区间牛顿法的点到参数曲线最小距离的计算方法[J].机电工程，2010，27(1):82-84.

[10]吴泽琦，吴根忠.基于遗传算法优化的仿人足球机器人步态规划研究[J].机电工程，2012，29(11):1340-1344.

[11]史海青，郁 丰.基于遗传算法的蜂窝广域空基伪卫星网络布局优化[J].兵工自动化，2013，32(9):68-72.

[12]王 超，黄 波，贾春兰，等.考虑加工质量和生产成本的柔性作业车间调度问题研究[J].机械，2012，39(12):10-15.

[13]方水良，姚嫣菲，赵诗奎.基于遗传算法的柔性车间多目标优化调度[J].机电工程，2011，28(3):269-274.