普氏摆运动规律研究

王振朝，周 阳，周 玉，张自力，董爱国，王亚芳

(中国地质大学(北京) 数理学院,北京 100083)

1 普氏摆现象简介

1922年，德国物理学家Carl Pulfrich发现了一个现象[1]，当用绳子悬吊的重摆在平面内作往复摆动时，如果用1块茶色镜遮住1只眼睛，同时睁眼看到的摆的运动轨迹会从单摆轨迹变为类似椭圆的立体轨迹，这种现象被后人称为“普氏摆现象”. 实验装置如图1所示，装置中间有重摆，周围有数根固定的柱子，用作参考物，戴上眼镜后观察重摆更有立体感. 后来的研究表明，在动态噪音模式下也存在类普氏摆现象[2]. 在应用方面，除了用于科学演示外，普氏摆现象还是Circlescan 4D的核心[3]，是未来立体电影研发的依据.

图1 普氏摆实验装置

普氏摆现象产生的机理一直有争议，现在广为大家所接受的解释是：相对于未遮挡眼睛而言，被光衰减镜遮挡的眼睛接收刺激信号有一定的延迟[4-8]，约0.01 s[9]，正因为延迟，有光衰减镜的那一只眼要比另一只眼晚看到单摆，产生深度上的错觉[10]，从而看到立体的轨迹.

基于普氏摆的产生机理，本文推导了普氏摆运动规律的数学表达式，并对影响普氏摆演示效果的一些因素进行了分析讨论.

2 数学模型的建立

以摆球运动的最低点为原点，摆球摆动平面为x-z平面建立坐标系，双眼在x-y平面，假设右眼戴镜片，当小球自右向左运动时，左眼看到的小球在A的位置，由于时间延迟此时右眼看到的小球在A′位置，双眼交汇的虚像位置为P，如图2所示，摆线长为l，小球释放的初始高度为h，人眼距摆平面的距离为d, 瞳距为d′, 在任意点小球的速度设为v，可以分解为水平方向的v1和竖直方向的v2，视线与小球最低点水平. 因为眼睛的延迟时间很短(0.01 s)，在推导中以A点的速率作为摆球从A到A′的平均速率. 另外，为了简化问题，假设摆球在理想条件下摆动，满足能量守恒，因此摆球运动满足：

图2 摆球运动示意图

3 运动规律的研究

3.1 水平方向的运动

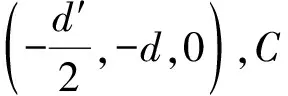
代入表达式得：

图3 小球在x-y平面的投影图(自右向左运动)

当小球自左向右运动时，如图4所示，推导过程类似，PD=-y，有：

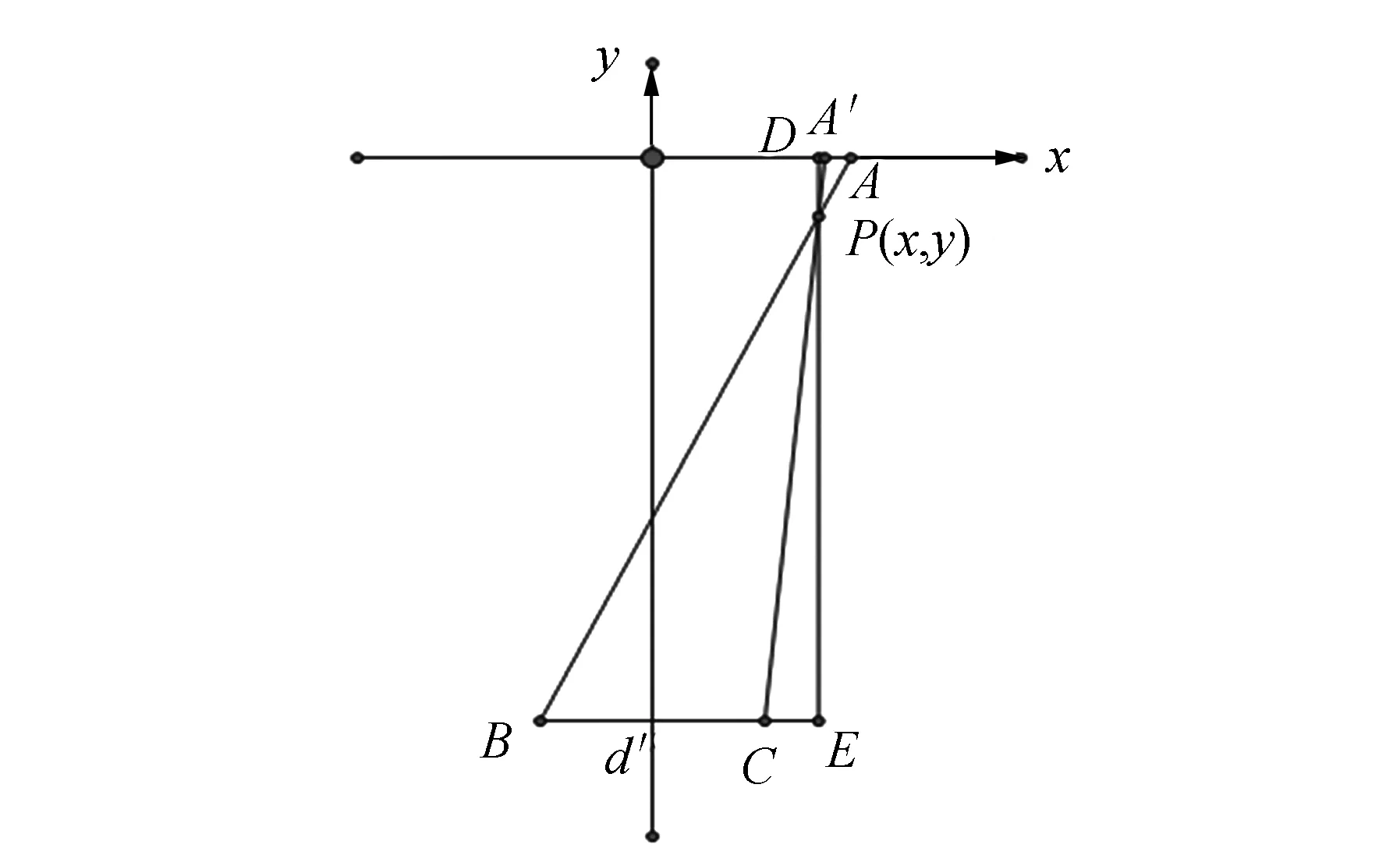
图4 小球在x-y平面的投影图(自左向右运动)

3.2 竖直方向的运动

同理，在竖直方向可以将三维图投影到y-z平面上，得到如图5的示意图，此时B和C重合，A和A′近似重合，过P作PG垂直于y轴. 则存在相似三角形，得到：

代入表达式得：

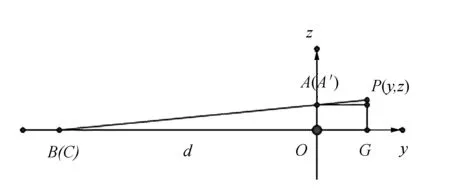
图5 小球在y-z平面投影图

3.3 运动方程的建立

通过前面的推导，只要联立(1)～(3)和(6)式，就可以得到，当小球自右向左运动时，有：

(7)

当小球自左向右运动时，有：

(8)

3.4 普氏摆运动规律的图示

根据方程(7)和(8)，利用Matlab给出普氏摆运动的图形，如图6～7所示，其中l=0.5 m,h=0.1 m,d=1.0 m,d′=0.07 m，t=0.01 s.

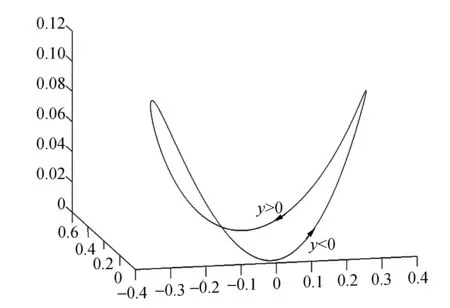
图6 三维图像

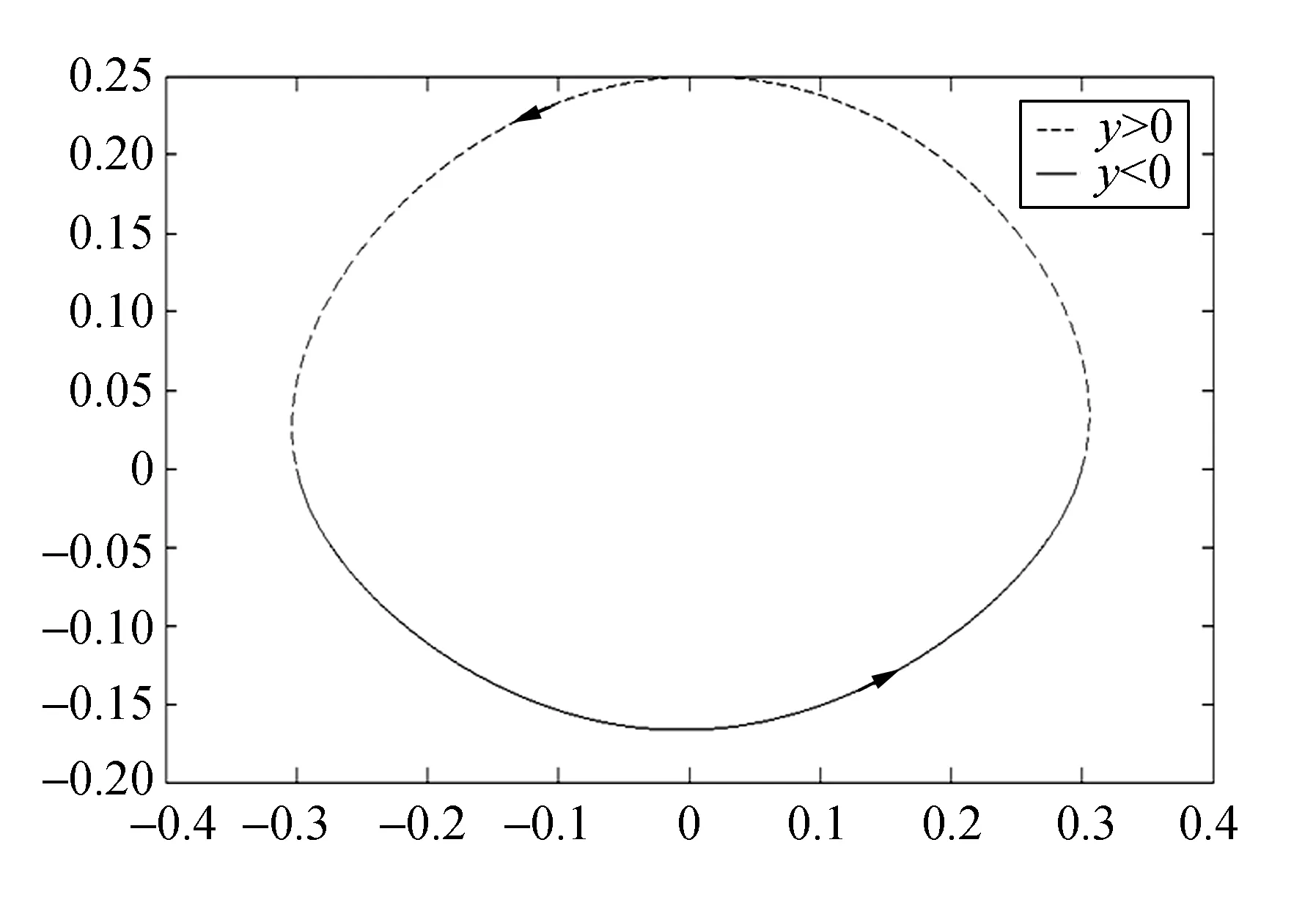
图7 投影到x-y平面

从图7可以看出，投影到x-y平面上的图像类似于椭圆形，但不是标准的椭圆，该图形关于x轴不对称.

4 分析和讨论

4.1 延迟时间的影响

方程(7)和(8)中y分量上下同时除以Δt，可以得到

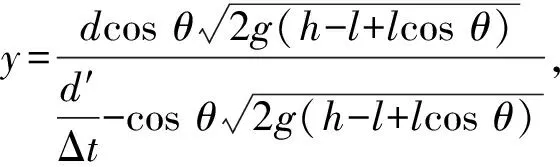
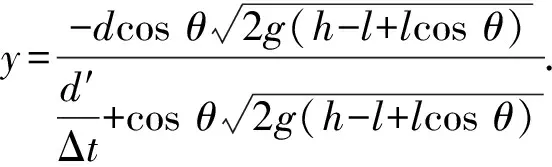
所以，延迟时间越长，|y|越大，摆球偏离摆平面的幅度越大，现象越明显，但是由于延迟时间涉及普氏摆现象的形成机制，Δt是不是常量，是否因人而异都是需要探讨的问题.

4.2 人眼距摆的距离的影响

通过方程(7)和(8)中y分量，可以看出，d增大，|y|越大，也就是小球前后摆动的幅度越大，这一结论和实际实验中观察到的现象一致.

4.3 摆球最大高度的影响

方程(7)和(8)中y分量上下同时除以v，得到：

可以看出，v越大，y越大，而摆球的最大高度决定了小球的最大速度，因此摆球初始高度h越大，现象越明显，这和实验中观察到的现象一致.

5 结束语

推导了普氏摆运动的像点轨迹方程，并对其方程进行了分析讨论. 通过方程可知，普氏摆在人眼中的运动轨迹是近似椭圆形但不是标准椭圆形，其图形关于摆平面不对称，略微向摆平面的后方偏移，影响其演示效果的主要有延迟时间、人眼距摆平面的距离、摆球释放的高度等.

参考文献：

[1] Pulfrich C.Die Stereoskopie im Dienste der isochromem und herterochromen photometrie[J]. Naturwissenschaft,1922,10:553-564.

[2] Tyler C W. Stereopsis in dynamic visual noise [J].Nature, 1974,250:781-782.

[3] 孙为民，刘宪国. Pulfrich(普尔弗里希)现象分析[J]. 高师理科学刊，2005,25(4):23-24.

[4] Carney T, Paradiso M A, Freeman R D. A physiological correlate of the Pulfrich effect in cortical neurons of the cat [J].Vision Res., 1989,29:155-165.

[5] Akiyuki A, Izumi O, Freeman R D. Joint-encoding of motion and depth by visual cortical neurons: neural basis of the Pulfrich effect [J]. Nature Neuroscience, 2001,4:513-518.

[6] Jenny C A, Read, Bruce G C. Effect of interocular delay on disparity-selective vl neurons:relationship to stereoacuity and the pulfrich effect[J]. Journal of Neurophysiology, 2005,94(2):1541-1553.

[7] Read J C, Cumming B G. The stroboscopic Pulfrich effect is not evidence for the joint encoding of motion and depth [J]. Journal of Vision, 2005, 5(5):417-434.

[8] Read J C, Cumming B G. All Pulfrich-like illusions can be explained without joint encoding of motion and disparity [J]. Journal of Vison, 2005,5(11):901-927.

[9] 罗春霞. 神秘的普氏摆[J]. 中国高新技术企业，2008,24:327.

[10] Morgan M J, Thompson P. Apparent motion and the Pulfrich effect [J]. Perception, 1975,4:3-18.