第45届国际物理奥林匹克竞赛实验试题简介

张春玲,刘丽飒,宋 峰,刘玉斌

(南开大学 物理科学学院,天津 300071)

1 引 言

第45届国际物理奥林匹克竞赛于2014年7月11日至7月19日在哈萨克斯坦的阿斯塔纳举行,代表中国参赛的5名中学生全部获得了金牌．本届竞赛的实验题是一道大的光学题目,题名为“看见隐藏的现象！”,主要考查与光的偏振相关的知识． 因篇幅有限,我们对原题作缩略,提炼出主要问题,给出简要的试题解答,并对中国队选手的答题情况给出简短评论.

2 试题介绍

实验中用到的器件及其实物图如表1所示.

表1 实验中用到的器件及其实物图

续表

很多物质具有光学各向异性,光的折射率依赖于光的传播方向和偏振方向. 偏振片1的透振平面与偏振片表面的交线为O1O1′(如图1),光线入射到偏振片1上,通过偏振片后成为线偏振光,其电场矢量Eins的振动方向在偏振片1的透振平面内. 接着光线照射到各向异性光学薄片P上,P的光轴方向PP′在晶体平面内且与偏振片1的透振平面成45°. 在P内光可被分成2种：振动方向垂直于光轴的寻常光Eo和振动方向平行于光轴的非寻常光Ee. 这2种光波的折射率不同,其折射率差为Δn=no-ne，从光学薄片出射时两光波的相位差为Δφ=2πhΔn/λ(h为薄片厚度,λ为入射光在真空中的波长). 因此,出射光的偏振态发生改变,2种光合成为椭圆偏振光. 接着,光束照射到偏振片2上,偏振片2的透振平面与偏振片1的透振平面垂直.

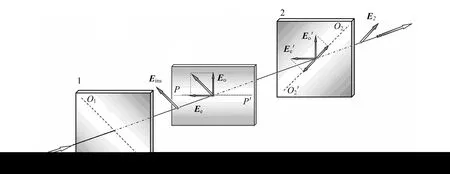
图1 研究光学各向异性的实验装置

经过简单推导可得光束经过光学薄片P和偏振片2后的光强为

其中，I0为照射到光学薄片上的光强,k为光通过光学薄片P和偏振片2的透过率系数,Δφ为经过光学薄片P后寻常光与非寻常光的相位差.

2.1 定性现象观察(3.5分)

2.1.1 偏振片(0.8分)

找出偏振片1和偏振片2的透振平面.

2.1.2 尺子(1.0分)

将LED固定在支架上,并连接好电源. 安装2个偏振片,有标号的一面(正面)朝向光源,确保2个偏振片的透振平面正交,即第二个偏振片后没有光线透出. 如图2～3,用1张白纸挡在第一个偏振片的正面,在2个偏振片中间放塑料尺子. 要求：找出塑料尺所有可能的光轴方向；分别估算在1号尺子上和2把尺子重叠这2种情况时, 大概在什么距离蓝光的相位差改变2π.

图2 把塑料尺固定在屏幕上

图3 观察塑料尺双折射现象的装置

2.1.3 塑料薄带(0.8分)

要求：找出薄带所有可能的光轴方向；将薄带用夹子固定在屏上,薄带的边缘与屏的边缘对齐,如图4,将屏放在2个偏振片中间,移动屏观察薄带上的色彩变化,以屏的左边缘作为x轴的零点,测量2个暗带的中间点的坐标(左边的坐标为xL,右边的坐标为xR).

图4 将可弯曲的塑料胶带固定在屏幕上

2.1.4 液晶盒(0.9分)

液晶是介于固态晶体和无定型液体之间的一种物质, 可以通过外加电场调整和控制其分子取向. 液晶具有各向异性,有2个折射率. 各向异性现象的效果依赖于外加的交流(AC)电压. 液晶盒由2个玻璃片组成,玻璃片的内表面镀有透明的导体层,2个玻璃片之间是薄薄的液晶层,玻璃片上焊有导线以连接AC电源. 不加电压时,液晶的长分子的方向平行于玻璃片,分子的方向与晶体的光轴一致. 将液晶盒放置在2个偏振片中间,并连上电源. 改变加在液晶盒上的电压,观察透过液晶盒的光的色彩变化. 要求：加在液晶盒上的电压为零和最大电压情况下,观察并确定所有可能的光轴方向,并在答题卡上标出来,设z轴为竖直方向；测量当液晶分子轴向发生90°突变时,加在液晶盒上的电压Ucr.

2.2 测量(16.5分)

将激光、偏振片1、有开口的屏幕以及光电探测器(1个光电二极管)固定在底座上. 调整实验装置,使激光束通过起偏器和屏幕的开口后正好照在光电二极管上. 利用旋钮5c使光电二极管上的光斑尺寸为5～6 mm.

激光器出射的是线偏振光. 用旋转圆盘5a来调整激光的偏振方向,使激光束基本上全部通过第一个偏振片,并且椭圆形光斑的长轴在竖直方向. 安装偏振片2,确保2个偏振片是正交的. 图5为安装屏幕之后的整套实验装置.

图5 测量塑料尺透射光的装置

2.2.1 研究光电二极管 (3.2 分)

采用光电二极管测量光强,其电动势是照射光强度的复杂函数,电路如图6所示. 万用表测直流(DC)电压依赖于照射光强度和可变电阻器的阻值. 下面实验的主要目标是选择电阻的最佳值,使电阻上的电压值与照射在光电二极管上的光强成正比.

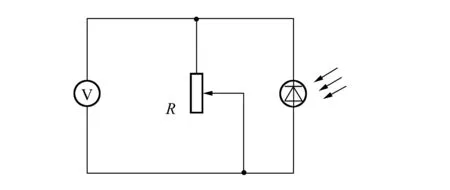
图6 测量光电二极管电动势的电路

从光学座上取下第二个偏振片和屏,用夹子将减弱光强的衰减片固定在偏振片的后面,如图7所示. 被测电压的最大值必须超过300 mV. 利用万用表测量电阻器的电阻值和电阻器上的电压,将开关放在恰当的位置,从而能够采用1个万用表既能测量电阻也能测量电压,也就是只通过打开和合上开关以及调节万用表挡位就能够测量,而不用断开电路.

图7 将滤光片固定于偏振片上

要求：画出电路图,确保开关的位置能够方便测量电阻器上的电压和电阻；在照射光强度为最大值(滤光片的数量n=0)和最小值(滤光片的数量n=5)时,测定电阻器上的电压与电阻的函数关系,在同一张图上画出相应的2条关系曲线,标出2条曲线的电压差值最大的电阻范围；测量电阻器上的电压U与滤光片数量n=0,1,2,3,4,5的关系(必须采用3个不同的电阻值,大约是30 kΩ, 20 kΩ和10 kΩ),将相应函数关系线画在同一张图上,注意选取合适的坐标以能够说明电阻器上的电阻是否与照射在光电二极管上的光强成线性关系,并根据上面提到的3个电阻值,选择最佳电阻值Ropt,再使用此电阻测量不同光强下的电压并作图. 利用获得的数据,计算滤光片的透过率γ=Itr/Iinc,估计误差,这里Itr为透射光强,Iinc为入射光强.

2.2.2 透过塑料尺的光(5.4 分)

在后续实验中必须使用上面选定的最佳电阻值,光强采用相对单位mV,数值上等于电阻器上的电压值. 在本部分中使用图5中的光路图,将塑料尺放在2个偏振片之间 ,如图2用夹子把尺子夹在带有开口的屏上,必须和屏上所画的直线重合,确保提供的2把尺子显示双折射现象. 把一把尺子叠放在另外一把尺子上, 当光通过时,观察图样.

要求：测量透射光强与光入射到尺子的位置坐标x(0～10 cm)的关系. 要分别测量所提供的每把尺子以及2把尺子叠在一起的情况. 在每种情况下,要测出电压的最大值. 在同一张图中画出每种情况对应的关系曲线.

对每把尺子,计算x从0到7 cm所对应的寻常光和非常光之间的相位差Δφ,在图中作出对应的关系线. 写出计算时使用的所有公式. [注意无法通过式(1)直接推出相位差,要正确地计算相位差,还需要一些其他物理条件.]

假定2把尺子各自满足线性关系：

Δφ1=a1x+b1,

Δφ2=a2x+b2,

分别确定尺子1和2各系数的数值.

利用前面所得到数据,计算2把尺子叠在一起时透射光强的理论值. 写下计算时使用的所有公式. 在此小题前面部分的实验图中加上计算得到的理论曲线.

2.2.3 液晶盒 (4.5 分)

将液晶盒如图8放在2个偏振片间. 要求：测量透射光的强度与液晶盒所加电压的关系,作图画出相应的关系线. 计算当电源与液晶盒未连接时,寻常光和非常光的相位差Δφ. 液晶盒上所加电压在很宽的范围内,寻常光和非常光的相位差与所加电压之间的关系为

Δφ=CUβ,

利用所得数据画图,确定上式适用的区间,计算指数β的数值.

图8 测量液晶盒特性的装置

2.2.4 光透过弯曲塑料薄带(3.4分)

按照2.1.3部分的描述把薄带安在屏上. 要求：测量透过光学系统后的光强与光入射到薄带时的光点坐标x的函数关系,x的测量范围为薄带中心的±20 mm，作图画出相应的关系曲线. 计算薄带不弯曲时寻常光和非寻常光的相位差Δφ,已知Δφ处于10π到12π间.

薄带靠近中心部分近似是半径为R的圆弧. 理论上相位差Δφ与距薄带中心的距离z(z≪R)满足如下关系

式中n=1.4是塑料薄带的折射率. 用前面几部分得到的数据,计算靠近薄带中心部分圆弧的曲率半径R.

3 简要解答和中国队学生答题情况分析

3.1 定性观察部分

偏振片1和偏振片2的透振平面如图9(a)所示. 经过国内培训,学生都知道通过旋转偏振片,透射光强最小时第二个偏振片的透振平面与第一个偏振片的透振平面垂直. 但是一些学生在做此题时感到困惑,因为此题的难度在于判断第一个偏振片的透振平面. 如果在答题时没有思路,但是能够仔细读题,就会在仪器介绍部分和2.2部分找到线索. 首先仪器介绍部分明确写出“偏振片的偏振方向与水平方向夹角为45°”,可以帮助学生初步判断透振平面的方向. 其次2.2部分提到“激光器出射的是线偏振光” ,如果学生据此能够知道激光光斑的方向就是其振动方向,就可以通过旋转第一个偏振片,判断出光强最小时偏振片的透振平面与激光光斑的方向垂直. 如果在读题时没有注意到提示线索,还可以利用布儒斯特角. 自然光在电介质界面上反射时,一般情况下反射光是部分偏振光,但是当入射角为布儒斯特角时反射光是线偏振光,其振动方向与入射面垂直. 通过将LED以布儒斯特角照射在白屏上,让反射光入射偏振片,然后转动偏振片,找到消光的位置,这时偏振片的透光平面刚好和反射线偏振光的偏振方向垂直.

塑料尺所有可能的光轴方向如图9(b)所示,为平行和垂直尺子的长边方向. 单独1号尺子和2把尺子叠放时,大概相距12 cm和8 cm时蓝光的相位差改变2π. 塑料薄带的光轴方向如图9(c)所示,与尺子成10°,左边暗带中间点的坐标xL=3.5 cm,右边暗带中间点的坐标xR=7.5 cm. 加在液晶盒上的电压为零和最大电压情况下的光轴方向如图9(d)所示,当液晶分子轴向发生90°突变时,加在液晶盒上的电压Ucr=2 V.

(a)

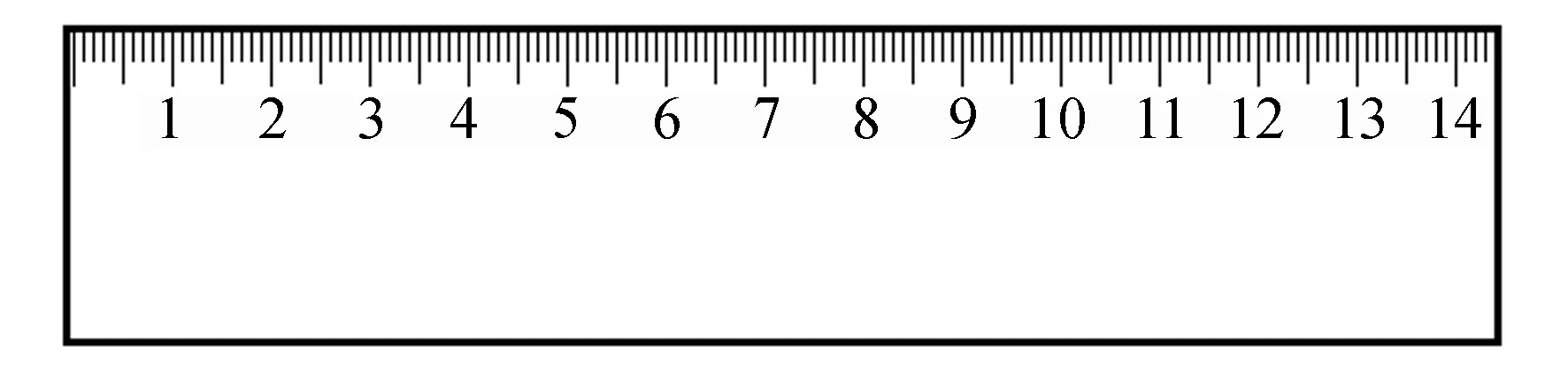
(b)

(c)

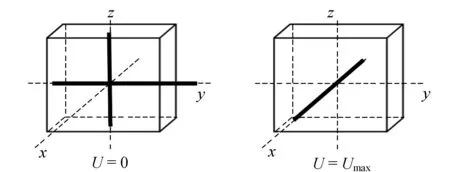
(d)图9 定性实验观察部分不同部件的透振平面和光轴方向

3.2 测量部分

3.2.1 研究光电二极管

电路图如图6所示，需要在图6的电阻和光电二极管之间加开关. 在照射光强度为最大值和最小值时,电阻器上的电压与电阻的关系如图10(a),图中阴影部分2条曲线的电压差值最大. 电阻器上的电压U与滤光片数量的关系如表2所示,透过滤光片之后的光强与滤光片的数量之间的关系为In=I0γn,如果测得的电压与光强成比例,则有Un=U0γn,为了验证此关系,只需画出lnU与n的关系lnUn=lnU0+nlnγ,如图10(b),根据3条曲线特点,选择最佳电阻值Ropt=5 kΩ,在使用此电阻时测得的不同光强下的电压画在图10(b)中,根据最小二乘法计算出滤光片的透过率γ=0.59±0.02.

(a)

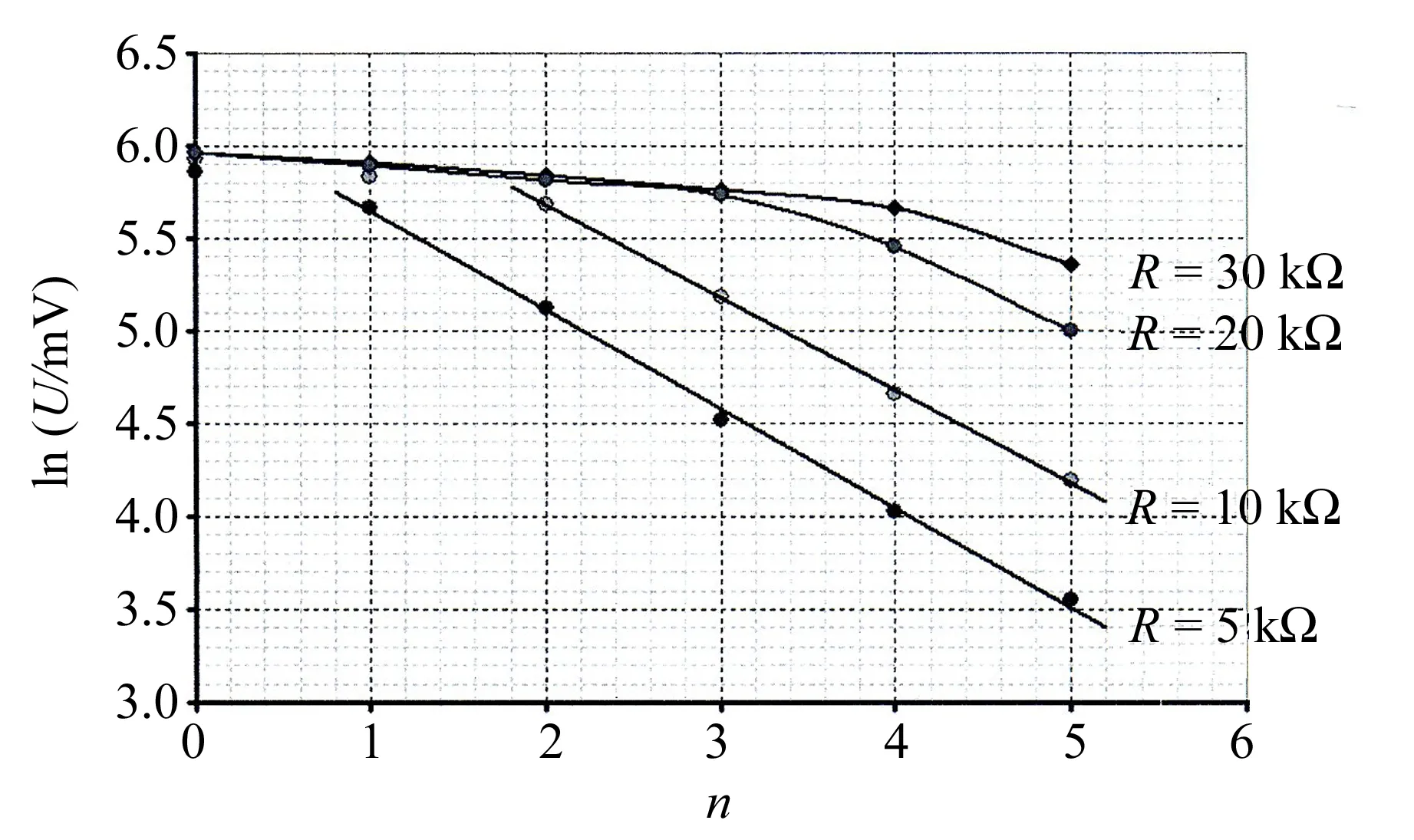
(b)图10 确定最佳电阻时的实验曲线

表2 电阻器上的电压U与滤光片数量的关系

注：R1=5.1 kΩ,R2=29.9 kΩ,R3=20.4 kΩ,R4=10.1 kΩ,

U1,U2,U3,U4对应R1,R2,R3,R4两端的电压.

当2个实验参量之间是简单的线性关系时,中国队的学生能够轻易地画出参量之间的关系曲线,但是当2个参量之间不是明显的线性关系时,个别学生还是依据惯性思维把它们往线性关系上硬套,而不是去看看他们是不是更符合幂函数或者指数函数的关系. 虽然考试时时间有限是理由,但是在这样的大型比赛中因为这方面能力的欠缺而丢失本题的分数,进而对后面的分数产生影响确实是非常可惜.

3.2.2 透过塑料尺的光

每把尺子和2把尺子叠放,尺子坐标x与透射光强数据见表3,关系曲线见图11(a).

表3 尺子坐标x与透射光强、寻常光和非常光的相位差

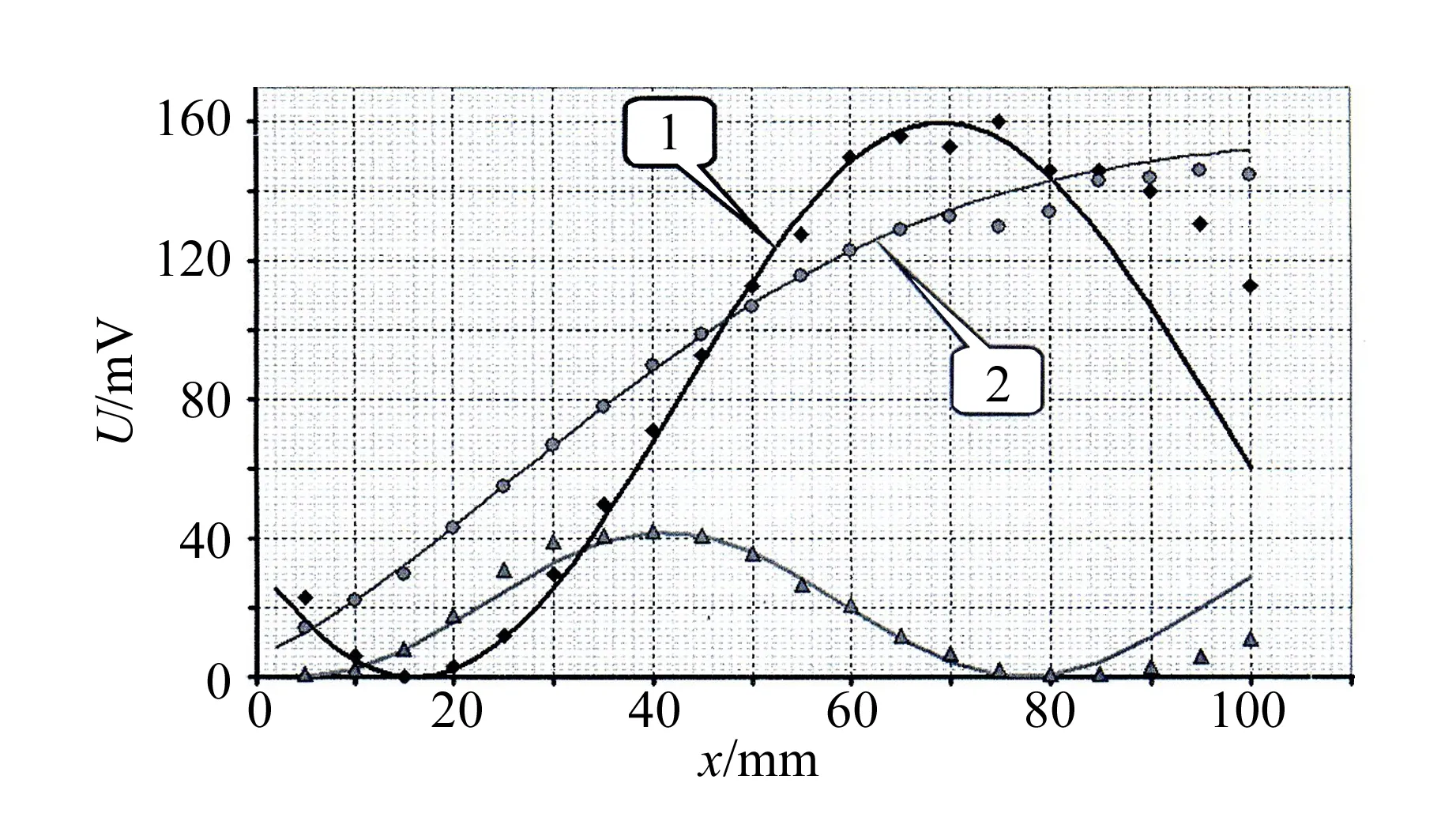
(a)

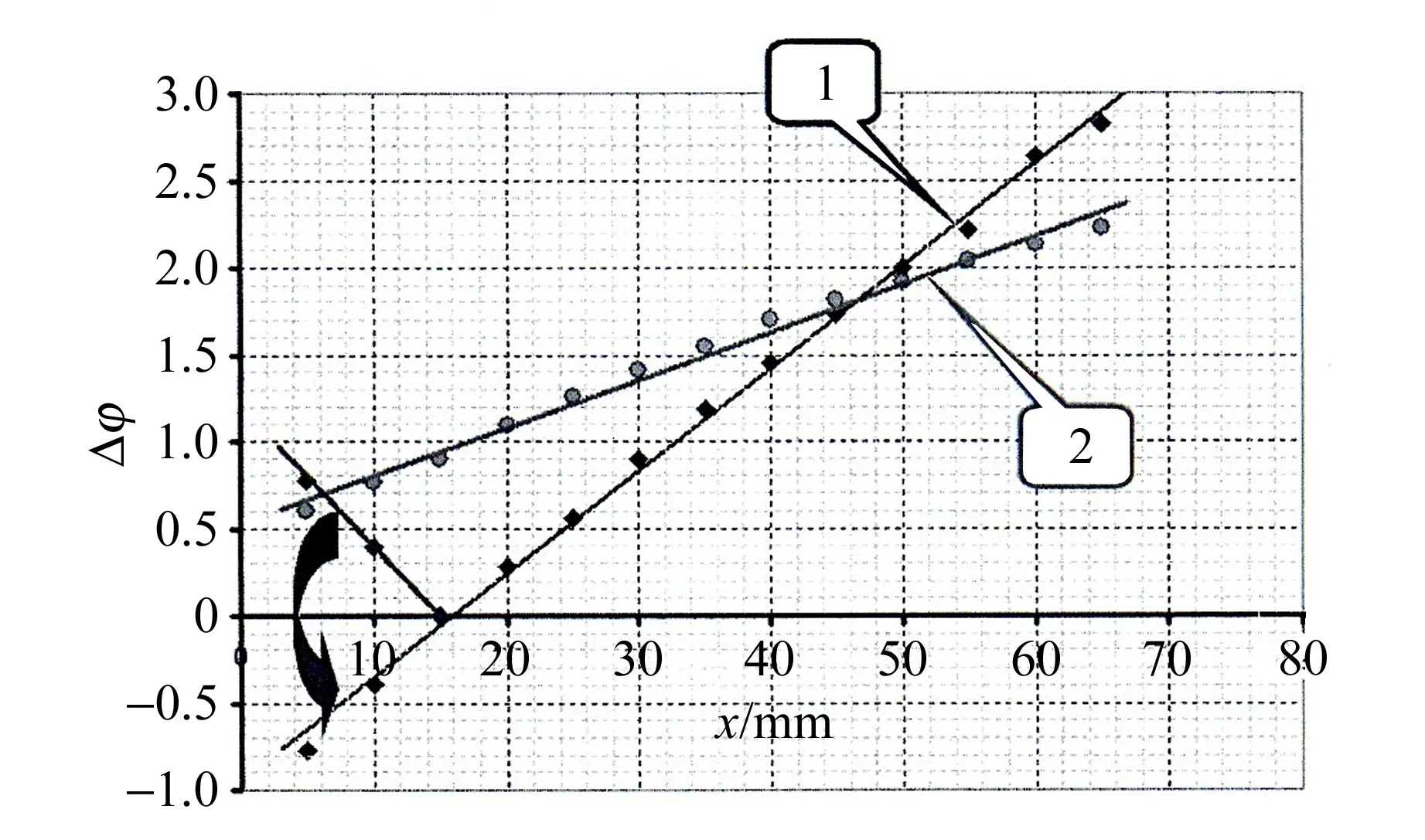
(b)图11 尺子坐标与透射光强度、相位差的关系

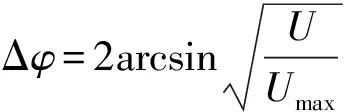
最小二乘法得到的结果为

Δφ1=0.059x-0.94,

Δφ2=0.028x+0.52.

2把尺子叠在一起时,理论上来说相移就是简单的相加:

此处Umax是从实验结果得到的2把尺子叠在一起时测得的最大电压. 将计算得到的理论值列在表3中,并加画在图11(a)上(此处没有给出).

3.3 液晶盒

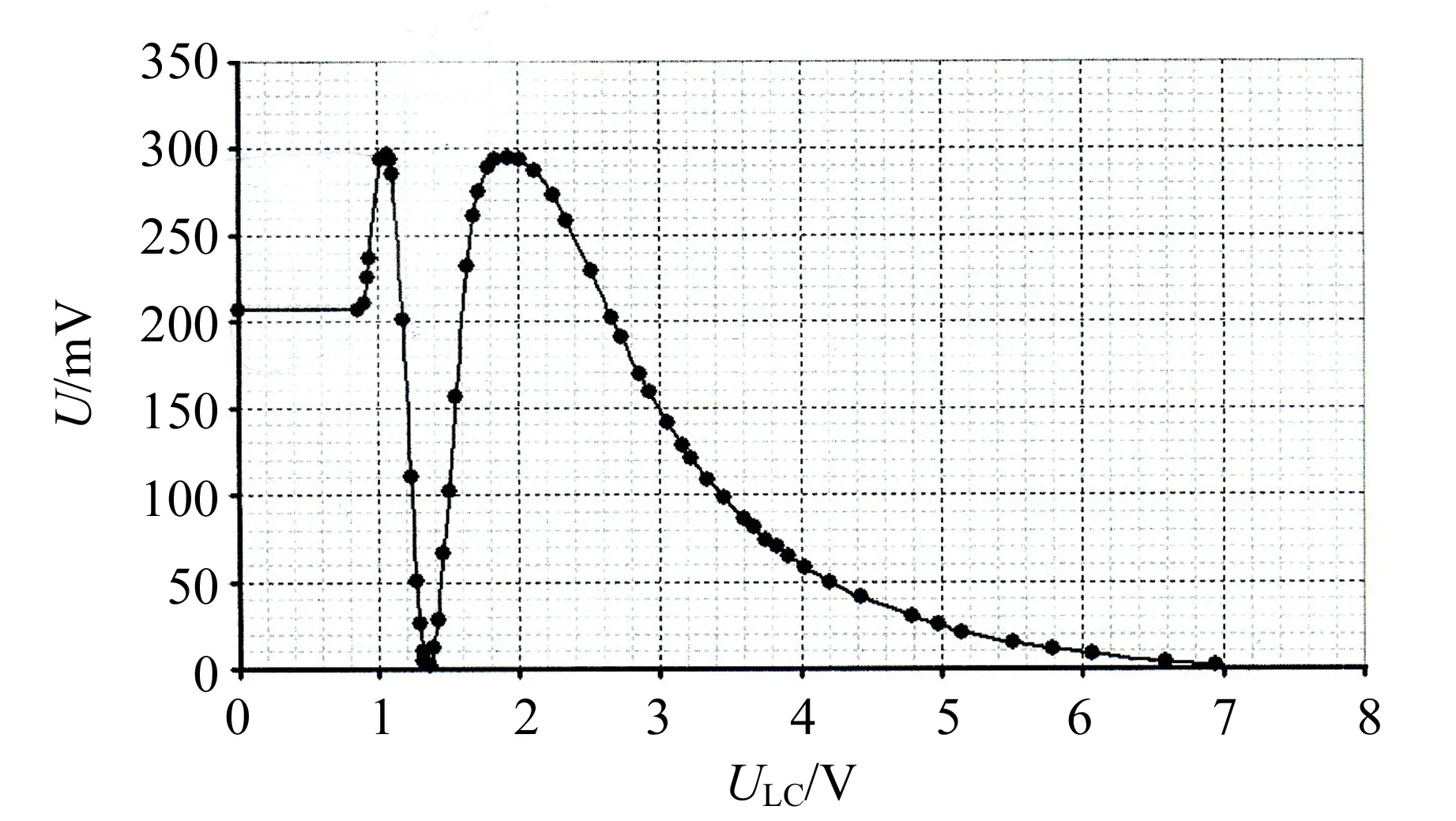
液晶盒上所加电压与和光电探测器上的电压关系如图12(a). 为了后面计算相位差,必须为(2)式选择正确的根. 因为液晶盒上所加电压ULC的值比较大时,光电探测器上的电压趋于0,Δφ→0,所以

计算得到的相位差如图12(b),电压为0时的相位差Δφ0=10.6.

为了验证幂函数Δφ=CUβ的适用性,画幂函数图如图12(c). 由图可知在1～5 V范围内,函数基本是线性的. 函数的幂指数等于直线的斜率,数值为β≈1.75.

(a)

(b)

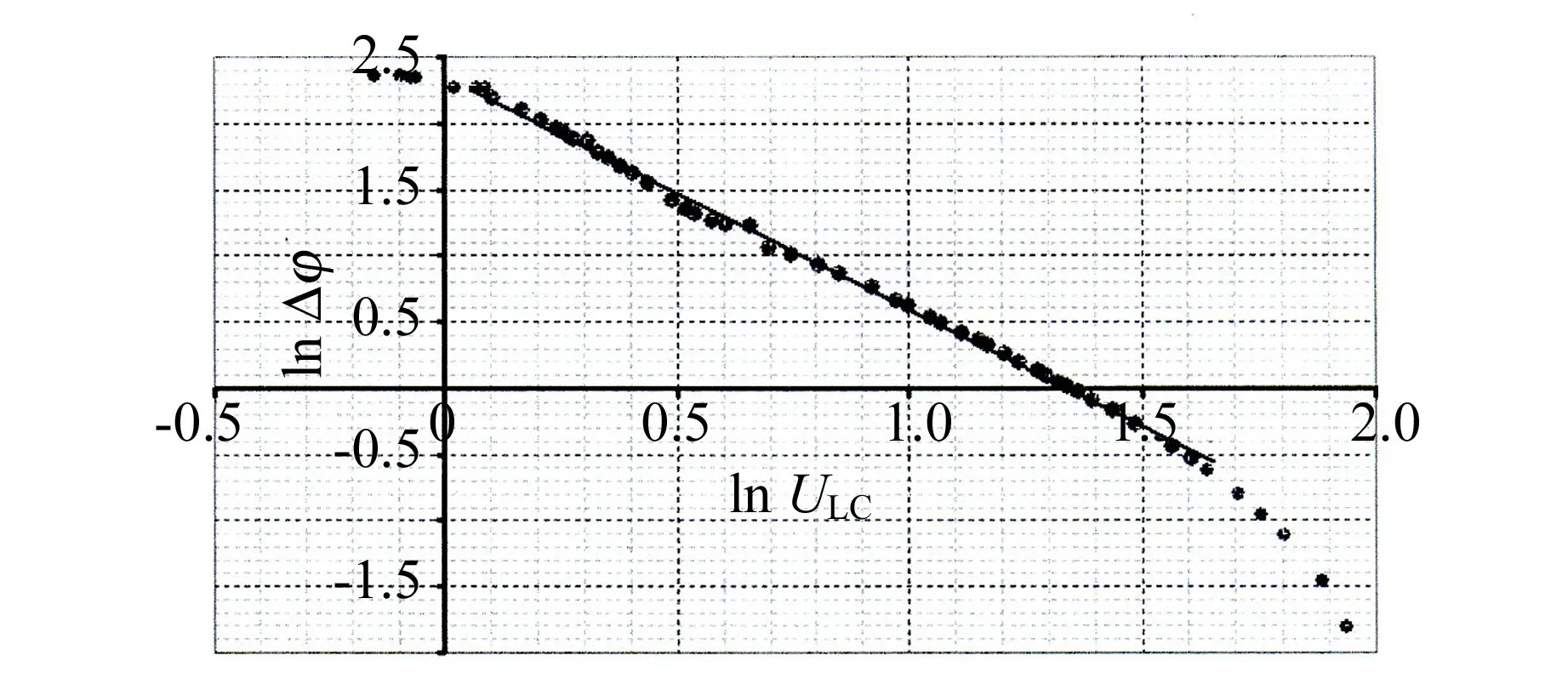
(c)图12 液晶盒上所加电压与光电探测器上的电压、相位差的关系

3.4 光通过塑料薄带

光强与光点照到薄带位置坐标x的关系如图13(a). 曲线形状显示Δφ0依赖于光强和相位差之间关系的上升部分,可以计算出

这里h为薄带厚度. 因此,透射之后寻常光与非寻常光相位差

(a)

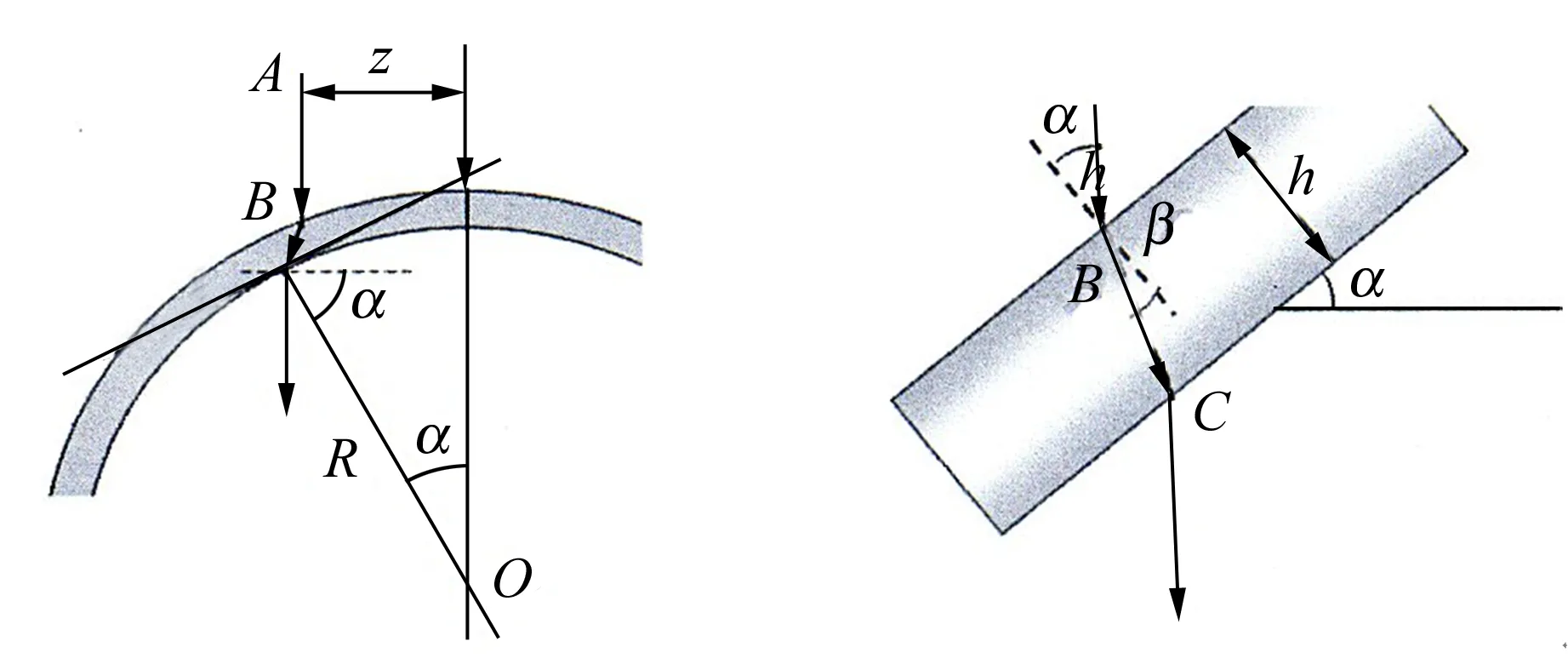
(b)图13 薄带相对中心的光强和薄带圆弧区光路示意图

这样,要确定曲率半径,需要分析相位差与薄带中心距离平方的函数关系,画出对应关系图后可以发现其中间部分近似为z的抛物线函数Δφ=az2+b. 为了确定函数的系数,画出Δφ与z2的关系图,用最小二乘法得a=0.010 4 mm-1,b=2.45,但是需要加上2π得到b的数值.

4 结束语

近2年亚洲物理奥赛和国际物理奥赛的实验部分都有一个共同的特点,就是每次实验考试都是1道大的综合题目. 但是虽然是1道题目,却是力电结合、力光结合或者光电结合. 这样做的好处是每道题都是由浅入深,能够比较系统地考察学生的实验水平. 即使实验水平不高的学生也会有入手点,能够拿到一定的基础分,而实验水平高的同学,能够有更多的时间去完成更多的实验内容,取得更高的分数.

参考文献：

[1] 吕斯骅,段家忯. 新编基础物理实验[M]. 北京：高等教育出版社,2006．

[2] 张春玲,宋峰,刘玉斌,等. 第44届国际物理奥林匹克竞赛实验试题简介[J]. 物理实验,2013,33(12)：13-17,20.

[3] 张春玲,刘丽飒,宋峰,等. 第15届亚洲物理奥林匹克竞赛实验试题简介[J]. 物理实验,2014,34(8)：14-19,24.

[4] 张春玲,宋峰,张天浩,等. 第14届亚洲物理奥林匹克竞赛实验试题与中国队学生实验能力分析[J]. 物理实验，2013,33(10)：18-26.