四模Lorenz系统的全局动力学研究

李德雪，尹社会

(河南工业职业技术学院，473000，河南，南阳)

四模Lorenz系统的全局动力学研究

李德雪，尹社会

(河南工业职业技术学院，473000，河南，南阳)

通过理论和数值模拟分析了一个四模Lorenz混沌系统的非线性特性和全局动力学行为。从对称性、耗散性、平衡点的稳定性、空间相图、时序波形图、分岔图等几个方面展示了系统具有丰富的动力学行为。

四模Lorenz混沌系统；分岔；耗散性；最终有界集

0 引言

混沌是指发生在确定性系统中的貌似随机的不规则运动，但与真正的随机运动又有着本质的区别。混沌运动在动力学上是确定的，运动的内部不稳定性导致了其运动的不可预测性。混沌系统产生的混沌运动具有几个重要特征：初值敏感性，临界水平和分形维[1]。奇怪吸引子是相空间中的一个点集，随着运动时间的增加，所有轨线都趋向于它。自从Lorenz在一个简单的三维自治系统中首先发现了蝴蝶混沌吸引子之后，又有新的混沌吸引子不断被发现，尤其是这些混沌系统的最终有界性被许多研究者所认识和研究[2-8]。本文进一步考虑文献[9]所提出的混沌系统，通过构造新的广义李雅普诺夫函数簇给出了新的吸引集的指数估计，并给出严格证明。数值仿真给出了系统的相图、时序波形图、分岔图等，结果表明了本文方法的可行性和有效性。

1 数学模型及其主要结果

王贺元等研究的一个四模Lorenz混沌系统的方程为[9]：

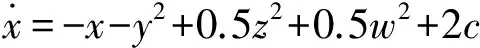
(1)

其中：(x,y,z,w)T∈R4为状态变量，c为系统实参数。

当c=11时，初值取(1,3,3,3)，系统(1)的轨线的相图如图1所示，各个变量随时间演化的时序波形图如图2所示。如果初值发生细微的变化，系统的行为会发生明显的变化，如图3所示为初值取(1,3,3,3)和(1,3.0001,3,3)的时序图形。

图1 系统(1)在参数c=11下的轨线相图

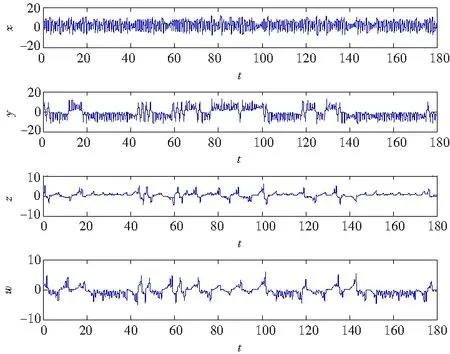
图2 系统(1)在参数c=11下各个变量的时序波形图

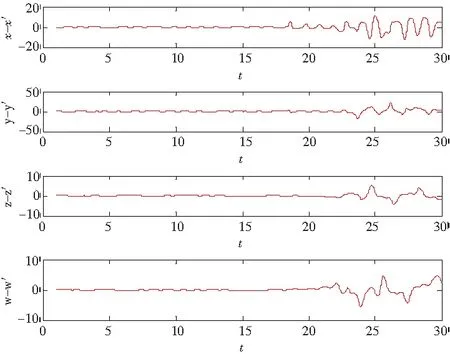
图3 系统(1)在参数c=11下初值(1,3,3,3)和(1,3.0001,3,3)下的敏感性时序波形图

随着参数c∈[0,20]的变化，系统表现出极限环(周期轨或拟周期轨)和奇怪吸引子等不同的非线性行为，即出现Hopf分叉和混沌现象。下面通过数值模拟可以验证图4中的结论。

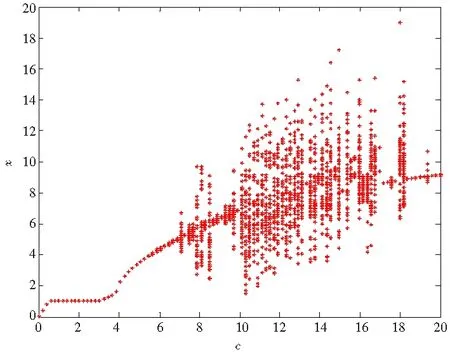
图4 系统(1)在x对c∈[0,20]的分岔图

图5 c=-1时系统(1)的相图

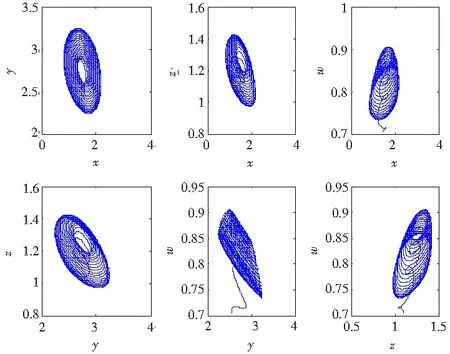
图6 c=4时系统(1)的相图

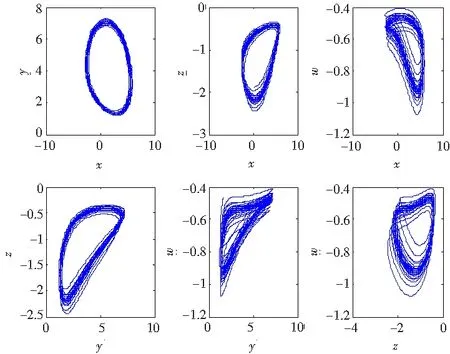
图7 c=8时系统(1)的相图

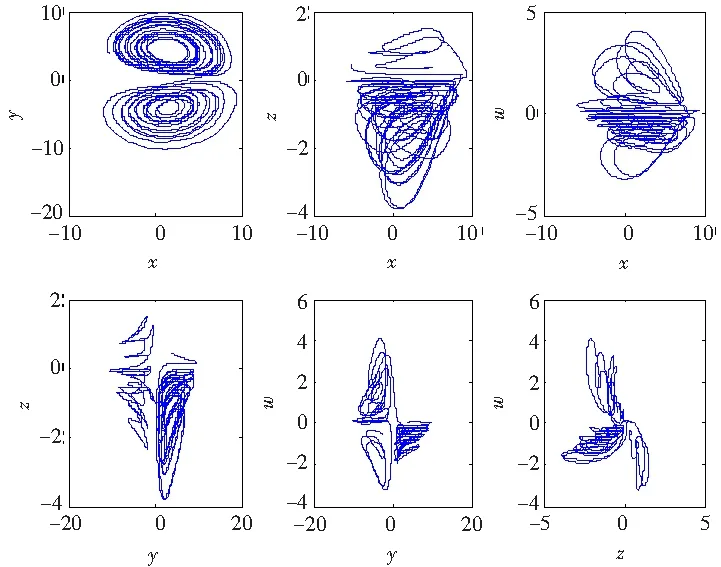
图8 c=9时系统(1)的相图

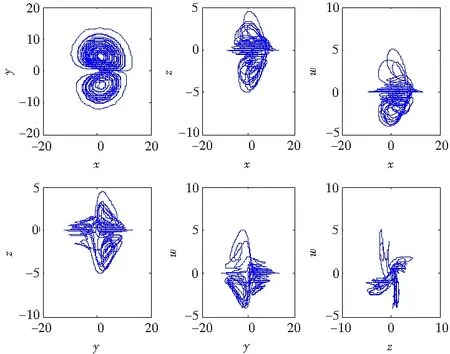
图9 c=10时系统(1)的相图

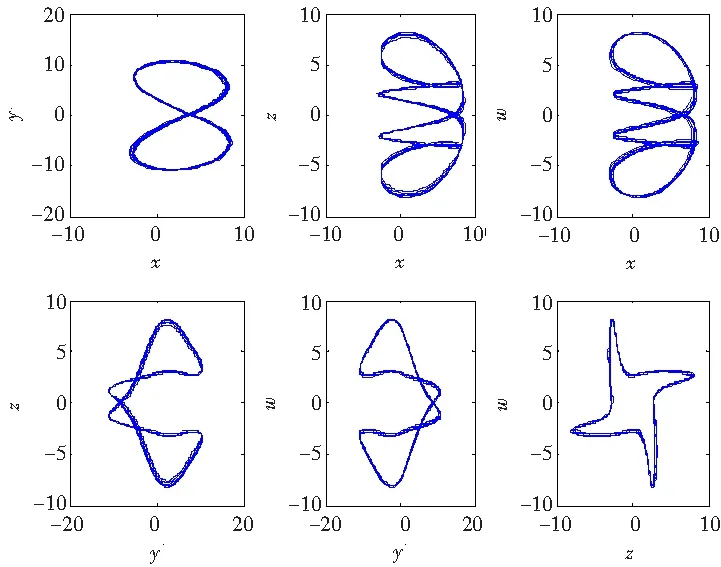
图10 c=16时系统(1)的相图

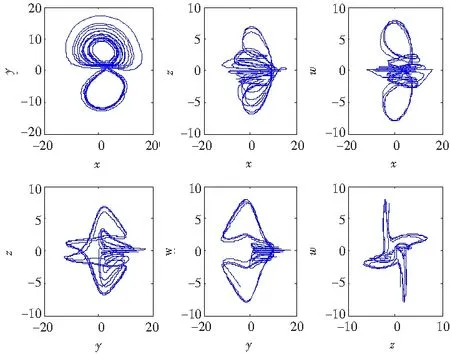
图11 c=17时系统(1)的相图

图12 c=18.7时系统(1)的相图

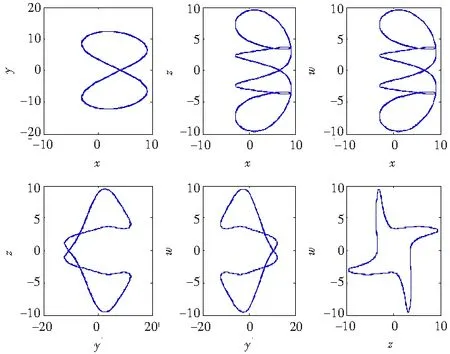
图13 c=20时系统(1)的相图

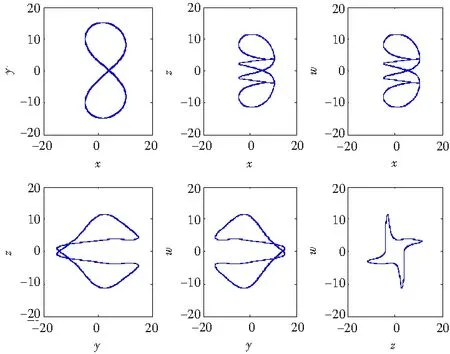
图14 c=30时系统(1)的相图

2 系统的界估计及数值仿真

定理1：集合Ω={(x,y,z,w)|(x-c)2+y2+z2+w2≤c2,(c∈R)}是系统(1)的正向不变集和最终有界集。

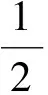
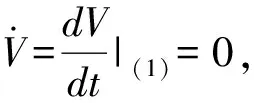
Γ={(x,y,z,w)|(x-c)2+y2+z2+w2=c2,(c∈R)}。

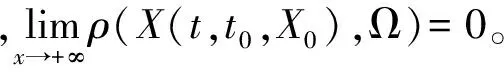
当参数c=11时，系统(1)的最终界估计为，Ω={(x,y,z,w)|(x-c)2+y2+z2+w2≤112},其中Ω在空间O-xzw空间中的投影如图15所示。

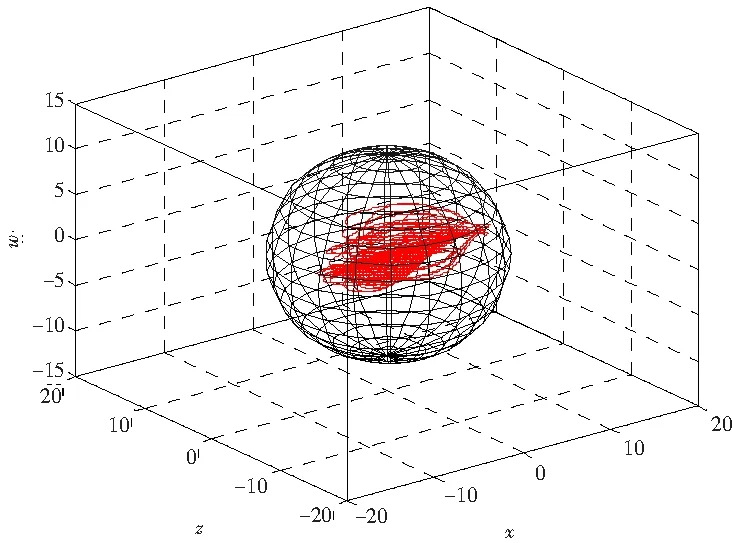
图15 当t→+∞时,系统(1)的正半轨线包含在三维球内

3 结论

本文研究了参数c变化时系统(1)的部分动力学行为和全局吸引集，并且给出了相应的计算机仿真。由于该系统具有丰富的动力学行为，其中混沌机理和分叉现象的研究还有待进一步探索。

[1] 吕金虎.混沌时间序列分析及其应用[M].武汉:武汉大学出版社,2002.

[2]Lorenz E N.Deterministic non-periods flows[J].J Atoms Sci,1963,20(2):130-141.

[3]尹社会,张勇,张付臣,等.基于Lorenz系统的强迫Lorenz混沌系统的动力学研究[J].东北师范大学学报(自然科学版),2014,46(1):42-47.

[4]尹社会,张勇,徐鹏飞.一个三维混沌系统的动力学行为及反馈同步[J].江西科学,2013,31(6):717-721.

[5]尹社会,张付臣,张光云,等.Navier-Stokes方程的动力学研究[J/OL].计算机工程与应用,http://www.cnki.net/kcms/detail/11.2127.TP.20130715.0936.008.html.

[6]张勇,尹社会,张付臣,等.新混沌系统的全局动力学研究[J/OL].计算机工程与应用,http://www.cnki.net/kcms/detail/11.2127.TP.20131017.1526.004.html.

[7]张勇,尹社会,张光云,等.多维混沌系统的全局动力学研究[J/OL].计算机工程与应用,http://www.cnki.net/kcms/detail/11.2127.TP.20131017.1526.005.html.

[8]屈元举,谢芳森,沈艳菲.一个新混沌系统的动力学研究和电路仿真[J].江西科学,2010,28(1):54-57.

[9]王贺元,鞠春贤.四模Lorenz系统的动力学行为及其数值模拟[J].高等学校计算数学学报,2010,32(2):99-105.

GlobalDynamicsofaNovelNonlinearChaoticSystem

LI Dexue,YIN Shehui

(Henan Polytechnic Institute,473000,Nanyang,Henan,PRC)

The globally exponential attractive set and non-linear characteristic properties of a four-modes Lorenz chaotic system is further investigated by theoretical and simulative analysis.From symmetry,dissipation,the stability of the equilibrium point,the phase diagram,time domain waveform and bifurcation diagram show the novel chaotic system has rich dynamic behavior.

four-modes chaotic system;bifurcation;dissipation;ultimate bounded set

2014-06-26;

2014-08-08

李德雪(1977-)，女，河南南阳人，硕士，讲师，主要从事非线性动力系统和混沌控制与同步等研究。

南阳市科学技术发展规划项目(2013GG035)。

10.13990/j.issn1001-3679.2014.05.003

O357.1；O241.82

A

1001-3679(2014)05-0578-04