基于Pro/E和LS-DYNA的齿轮线外啮合冲击研究

，， ，

(1.东北大学机械工程与自动化学院，辽宁 沈阳 110819；2.东北大学信息科学与工程学院，辽宁 沈阳 110819；3.中国人民解放军65631部队，辽宁 锦州 121300)

基于Pro/E和LS-DYNA的齿轮线外啮合冲击研究

佟操1，孙志礼1，冯真2，贾宁3

(1.东北大学机械工程与自动化学院，辽宁 沈阳 110819；2.东北大学信息科学与工程学院，辽宁 沈阳 110819；3.中国人民解放军65631部队，辽宁 锦州 121300)

0 引言

众所周知，齿轮的安装与制造误差对齿轮齿面接触应力和齿根弯曲应力有很大影响。但是迄今为止，还没有一种能够精确求解带有安装与制造误差齿轮接触应力与弯曲应力的有效方法。传统的方法是通过引入载荷系数，来考虑误差因素。但是这仅取决于人为经验，不可能精确计算带有各类随即因素的齿轮应力。

在齿轮啮合过程中，由于轮齿误差和轮齿变形，使轮齿产生“啮合合成基节误差”，使轮齿在啮入和啮出时的啮入点和啮出点偏离理论啮合线，从而使主、被动齿轮转动速度产生偏差和突变，引起啮入和啮出冲击力。研究表明，啮合冲击是导致齿轮传动振动、噪声和点蚀破坏的主要原因之一[1-4]。

从文献成果[5-10]来看，主要研究以振动理论为基础的离散模型较多，其动力学模型是基于假设只有弹性而无惯性和只有惯性没有弹性的质量块组成，此离散模型可以大大简化物理模型且有利于计算效率。然而，由于齿轮结构配置和几何形状复杂，同时齿轮啮合刚度随时间变化的非线性行为(由于移动的接触点、单双齿接触交替、啮合刚度不连续和齿侧间隙的影响)，故离散模型很难精确地描述齿轮系统的动力学特性。

通过大型三维建模软件Pro/E建立带有基节偏差的齿轮实体模型，采用全球著名的显式动力学软件LS-DYNA对1对直齿轮进行动力学计算，不需要任何额外的假设与简化，求解带有基节偏差的齿轮动态接触应力和弯曲应力特性。

1 齿轮啮合冲击碰撞相关理论

1.1 齿轮啮合冲击分析

在齿轮动力学中，将这种传递中齿对和齿对的交替过程称为轮齿啮合的过渡过程。一般说来，理想齿轮(无误差、无变形的齿轮)的过渡过程是平稳的。但是，由于实际的齿轮总是存在误差，而且在传递动力时也会产生弹性变形，因而在过渡过程中将产生冲击。由于轮齿误差和轮齿受载弹性变形所产生实际基节和理论基节的偏差，因此,在齿轮啮合过渡过程中，使得轮齿1的基节不等于轮齿2的基节。这样，轮齿在啮入点和啮出点会偏离理论啮合线，从而导致齿轮传动在啮合开始与结束时发生啮入与啮出冲击。

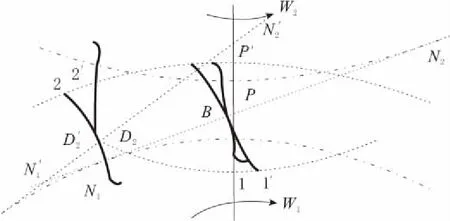
图1 齿轮啮入冲击

1.2 关于两接触弹性体的接触动力学相关理论

齿轮动力学平衡方程为:

(1)

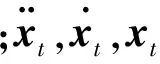
关于解法，LS-DYNA采用显式中心差分法，具体算法为：假定0,t1,t2,…,tn时刻的节点位移、速度与加速度均为已知，现求解tn+1(t+Δt)时刻的结构响应。中心差分法对加速度、速度的导数采用中心差分代替，即

(2)

将式(4)代入动力学基本方程，整理后得:

(3)

求解上式线性方程组即可求得各时刻的节点位移向量，将其代入差分公式可求得对应的速度、加速度向量。

关于两物体A和B的接触问题，构型分别为VA和VB，边界面分别为ΩA和ΩB。A为主体(Master)，其接触面为主动面，物体B为从面(Slave)，其接触面为从动面。A与B接触时的非嵌入条件可以表示为:

VA∩VB=0

(4)

物体A与物体B不能互相重叠，在每一时步，对比ΩC面上物体A与B对比节点的坐标，或对比速率来实现位移协调条件,即

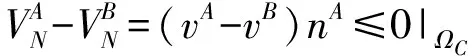
(5)

下标N表示接触法线方向。

接触面力应满足：

(6)

LS-DYNA显式动力学接触-碰撞算法采用对称罚函数法，对于从节点nS，搜索与它最近主节点mS。检查与其主节点上有关的所有主片，确定从节点nS穿透主表面时可能接触的主片。若主节点mS与从节点nS不相重，且满足式(9)时，从节点nS与主片Si发生接触。

(7)

Ci和Ci+1是主片Si在mS点的两条边矢量。矢量S是矢量g在主表面上的投影，g是从mS到nS的矢量。

S=g-(g·m)m

(8)

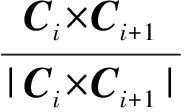
S=max(g·Ci/|Ci|)，i=1,2,…

(9)

从而确定了从节点nS在主片Si上可能的接触点C的位置。其中r是主片Si上任一点的位置矢量。接触点位置满足如下方程。

(10)

求解C坐标(ξc,ηc)。之后检查从节点nS是否穿透主片。若l=ni·[t-r(ξc,ηc)]<0，表示nS穿透主片Si，ni是在接触点处Si外向法线单位矢量，若l≥0，即nS没有穿透主表面。如果nS穿透主片Si，则在nS和接触点之间附加一个接触矢量，可计算主片Si各节点接触力。

2 齿轮副参数化模型的建立

如前节分析知，齿轮线外啮合冲击主要是由于大小齿轮基节偏差所致，故本节探讨关于带有基节偏差的齿轮实体模型生成的方法，传统的理想齿轮齿轮生成办法[10-11]，不再予以叙述，重点阐述在理想齿轮基础之上添加基节偏差参数化模型。

对于基节偏差，其定义为在基圆上同侧齿面的法相实际距离与工程距离之差。当齿轮存在不同齿距偏差时，体现在模型中的变化是齿轮齿廓位置的偏移。因此，在Pro/E中建立齿轮轮齿特征时应用“阵列”方法，围绕齿轮中心轴线，齿与齿间的阵列角度为360/Z，阵列的轮齿将均匀分布于齿轮外缘。

为了赋予阵列角度360/Z偏差值，直观体现到模型中便是基节偏差。

然而在建立带有基节偏差的齿轮，其难点就是基节偏差至阵列角度偏差的转化问题，在具体设计建模过程中，给定基节偏差Δ基节，通过式(13)转化为阵列角度偏差，并设置在关系式中,即

(11)

所以，在阵列齿轮时，阵列角度为:

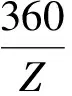
(12)

图2为生成带有基节偏差的齿轮，由于偏差较小，不易肉眼观察，故将此模型的基节偏差放大为0.1的效果图。

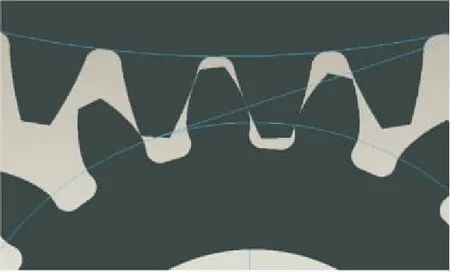
图2 误差齿轮Pro/E

从图2可以看出，后一对还齿轮即将进入啮合，且在线外啮合，从而为动力学仿真提供了生成带有基节偏差的实体模型。

3 数值求解

3.1 前处理

选择ANSYS作为前处理软件，选择适用于大变形分析的solid164体单元以及用于加载转速与转矩的shell163壳单元。对于solid164单元，选择单点高斯积分形式，shell163壳单元，单元为均匀厚度，厚度为0.1mm，选择S/R corotational Hughes-Liu面内多积分，以消除沙漏模态。齿轮的材料选择30CrNi3，质量密度为7.85×103kg/m3，弹性模量为2.06×1011Pa，泊松比为0.3。

3.2 有限元网格划分

对于有限单元网格，六面体相比四面体网格单元，能够得到较好的计算精度，且在相同计算精度下，可以使用较少的网格数量，从而提高计算速度，因此,使用solid164六面体划分网齿轮进行划分。

对于有限元算法本身的特性，其计算只是近似解，其计算的精度取决于网格质量。通常网格质量越好，密度越高，则计算精度越精确，但同时计算时间也大幅度增加。因此,选择较好的网格控制参数，才能保证计算的结果准确可行。控制网格参数的原则是重要部位加密(如齿面、齿根过渡圆角部位)，不重要的位置(如齿轮轮毂)网格密度可以适当的稀疏，这样不仅能保证重要部位的计算精度还能节省宝贵的计算时间，提高效率。

具体的操作步骤：首先采用solid164单元，选择一个适当的网格控制参数，控制适当的esize、lsize以控制齿轮齿根圆、过渡圆角、渐开线的网格密度，对其齿轮整体进行体扫掠，采用shell163单元在齿轮内表面对其划分网格，计算出当前接触位置的应力结果；然后将网格密度大小缩小1倍，再试验，直到同一位置2次计算结果相差很小时，则停止。此后网格密度继续增多，不会增加计算精度，只会使计算时间大幅度增加，因此,在动力学仿真之前，通过反复试验选取合适的网格密度，认为此时的网格密度为最佳。经过反复试验和对比，最终的齿轮网格划分如图3所示。

图3 齿轮有限单元模型

3.3 定义PART、接触和施加载荷

在ANSYS/LS-DYNA程序中，没有接触单元，只要定义可能接触的接触表面、接触类型以及与接触有关的一些参数，在计算过程中程序就能保证接触界面之间不发生穿透，并在接触界面相对运动时考虑摩擦力的作用。模型选用的接触类型是自动面面接触(ASTS)，此接触是最容易定义的接触类型而且不会花费过多的CPU时间。

把采用刚体上加载转矩转速。定义大小齿轮的内圈为刚性体，主动齿轮施加转速，被动轴施加阻力距，转速为900r/min，转矩为5 000N·mm。

3.4 修改K文件

改动的地方有以下几点需要注意：

a.由于模型计算量较大，导致系统的内存不足，无法满足计算需求，此时需要修改文件内存，将K文件第1行后面加上30×107，以满足内存需求。

b.LS-DYNA求解碰撞问题时，不能有初始穿透，固先处理初始穿透，在关键字*CONTROL_CONTACT中将参数IGNORE项改为1，可以很好地消除初始穿透引起不真实的应力。

c.几乎所有LS-DYNA的所有功能都能通过ANSYS命令流实现。但是，知道ANSYS只是将APDL命令转化为K文件，最终计算时都是采用LS-DYNA求解器，输入文件都是K文件，所以直接在更改K文件，会减少重建划分网格、建立模型等时间。通过大量尝试发现，ANSYS命令流不能完美地转化为LS-DYNA的K文件，例如在主动轮的刚体留有只具有绕Z轴转向自由度，对应K文件的参数值应为7，但是经过转换后为8，故此处需改动。

d.定义接触设置时，若要求的齿轮齿面接触应力，需输出对应文件，在LS-PrePost中才能调用。

4 数值仿真结果的验证与分析

4.1 理想齿轮啮合冲击的结果分析

在Pro/E中首先建立理想齿轮副模型，调整齿轮副啮合角度，使其第1对轮齿，第2对轮齿接近啮合的位置，此时对其啮合齿轮进行动力学仿真。对于弯曲应力的提取，在主动轮齿根部位提取相应单元，分别提取第1对、第2对轮齿的弯曲应力-时间曲线，如图4所示。

图4 理想无误差齿根弯曲应力

从图4可以看出,在双齿啮合区，由于2个轮齿共同参与啮合，每个轮齿啮合力峰值是单齿啮合区峰值的1/2；单齿啮合区啮合力峰值分别为208 MPa,212MPa，其最大值与理论值18 MPa，相差不大，其比值为1.133，即动载系数，与理论相符，印证了计算模型的正确性。

对于接触应力的提取，由于齿轮啮合接触点时刻变化，故其接触应力的提取不能通过选取单一节点。提取方式为：通过选取接触面上所有节点，认为其接触应力值最大曲线对应的节点位置为齿轮啮合接触相对应的节点位置。

如图5所示，对于第1对齿轮齿面上173号节点接触冲击最大，对于第2对齿轮齿面上466号节点接触冲击最大。

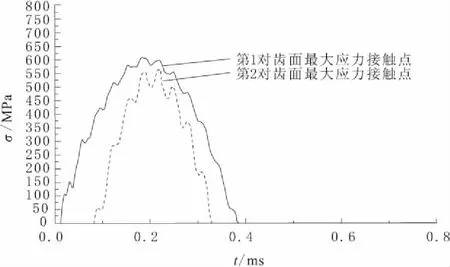
图5 理想无误差齿面最大接触应力

4.2 基节偏差对齿轮啮合冲击的影响

由第1.1节分析知，当主动轮基节小于从动轮基节时，是产生啮入冲击的主要因素。故分别选取主动轮基节偏差为正(基节减小方向)、从动轮基节偏差为负(基节增大方向)，再由第2节中建立的参数化齿轮生成所需要的模型。由模型结果可得出，随着齿轮的基节偏差增大，齿面所受冲击应力值也在增长，故在校核齿轮强度时，应考虑最大基节偏差时的接触应力作为最大校核应力，在冲击接触应力过大时，可以适当增加齿轮加工精度等级，以此来减少基节偏差。

5 结束语

齿轮接触应力和弯曲应力的理论分析与动态仿真结果基本吻合，验证了方法的正确性。对带有不同基节偏差的齿轮模型进行动力学分析，得出基节偏差对齿轮啮合冲击的应力状态具有十分重要的影响，即基节偏差越大，齿轮啮合冲击越严重。研究为齿轮强度的精确计算和设计提供了一种方法，在选择齿轮精度加工等级时，可以根据上述计算方法选择适当的齿轮基节偏差范围，使其能够承载当前的负载力矩与转速。对于研究齿轮连续体各类随即误差对齿轮减振降噪具有一定的理论价值。

[1] 李润方，王建军.齿轮系统动力学[M].上海：科学出版社,1997.

[2] 周长江，唐进元，钟志华.齿轮传动的线外啮合与冲击摩擦[J].机械工程学报,2008,44(3):75-79.

[3] 唐进元,刘 欣,戴 进.基于ANSYS/LS-DYNA的齿轮传动线外啮合冲击研究[J].振动与冲击,2007,26(9):40-44.

[4] 李 昌，韩 兴，孙志礼.基于Pro/E和ADAMS的齿轮啮合精确动力学仿真[J].机械与电子,2008,(1):55-58.

[5] Lin J，Parker R G.Analytical characterization of the unique properties of planetary gear free vibration[J].Journal of Vibration and Acoustics-transactions of the Asme,1999,121(3):316-321.

[6] Mcfadden P D，Cook J G，Forster L M.Decomposition of gear vibration signals by the generalized stransform[J].Mechanical Systems and Signal Processing,1999,13(5):691-707.

[7] Dalpiaz G，Rivola A，Rubini R.Effectiveness and sensitivity of vibration processing techniques for local fault detection in gears[J].Mechanical Systems and Signal Processing,2000,14(3):387-412.

[8] Antoni J，Bonnardot F，Raad A,et al.Cyclostationary modelling of rotating machine vibration signals[J].Mechanical Systems and Signal Processing,2004,18(6):1285-1314.

[9] Samuel P D，Pines D J.A review of vibration-based techniques for helicopter transmission diagnostics[J].Journal of Sound and Vibration,2005,282(1/2):475-508.

[10] 李常义,卢耀辉,周继伟.基于ANSYS的渐开线圆柱齿轮参数化造型与有限元建模及分析技[J].机械传动,2004,28(6):25-28.

[11] 何茂先,殷晨波,肖 乐.基于Pro/E的渐开线齿轮的参数化建模研究[J].机械与电子,2006,(3):72-75.

Research of Gear Meshing Impact Outside the Engagement Line Based on Pro/E and LS-DYNA

TONGCao1,SUNZhi-li1,FENGZhen2,JIANing3

(1.School of Mechanical Engineering and Automation,Northeastern University,Shenyang 110819,China;2.College of Information Science and Engineering,Northeastern University,Shenyang 110819,China;3.People’s Liberation Army of China,65631Troop,Jinzhou 121300,China)

首先基于Pro/E二次开发建立带有基节偏差的齿轮参数化模型，给出生成误差模型的方法和思路，从而保障了连续体齿轮动力学仿真顺利进行；采用ANSYS前处理功能，基于APDL命令流语言，对齿轮进行划分网格，给出划分网格的控制方法和划分思路，以保证求解计算精度高且计算时间快；采用显式动力学软件LS-DYNA对其进行动力学计算，从而实现精确求解齿轮连续体在啮合冲击过程中齿轮的动态弯曲应力和接触应力。

齿轮；基节偏差；线外啮合冲击；Pro/E；LS-DYNA；接触应力；弯曲应力

In this paper,firstly,a gear parametric model with base pitch error is established based on Pro/E secondary development,and given a method and idea to generate error model,therefore,it is guaranteed that continuous body gear dynamics is simulating successfully.the gear model is menshed based on APDL command flow language mesh by using ANSYS’s pre-processing function,and a meshing control method is given in order to ensure high accuracy and to calculate time fast.The explicit dynamics software LS-DYNA is introduced for the dynamics calculations,thereby,it is achieved that gear bending stress and contact stress during engagement impact is calculated accurately.

gear;base pitch error;impact outside the action line;Pro/E;LS-DYNA;contact stress;bending stress

2013-10-29

航空科学基金资助项目(20110450002)

TB53

A

1001-2257(2014)06-0010-05

佟操(1986-)，男，辽宁营口人,博士研究生,研究方向为齿轮系统动力学、齿轮传动系统虚拟可靠性试验;孙志礼(1957-)，男，山东巨野人,教授，博士研究生导师,研究方向为机械可靠性工程等。