自由界面模态综合求解系统的开发与应用

2014-04-10温争鸣胡于进

机械与电子 2014年6期

关键词：降阶综合法子结构

温争鸣，胡于进

（华中科技大学机械科学与工程学院，湖北武汉430074）

0 引言

自由界面模态综合法是复杂系统动力学分析的最有效的方法之一［1－2］。但是，该方法完全忽略了高阶截断模态的影响，结果的收敛性和精度均较差。因此，一些研究者［3－5］通过研究，形成了目前常用的双协调自由界面模态综合法。

虽然自由界面法在工程中已有了广泛的应用，但是这些应用大都仅仅针对某一工程实例。基于双协调自由界面模态综合法［6－7］开发通用性的求解系统，为自由界面模态综合法在工程中的应用提供有效工具。

1 双协调自由界面模态综合法

1.1 子结构降阶

将复杂系统按照其特点划分为若干个子结构，选取其中任一子结构为例来介绍子结构的降阶。设该子结构的无阻尼动力学方程为：

按照界面自由度和非界面自由度对上式进行分块，得：

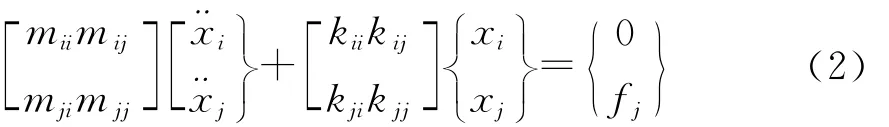
下标i和j分别表示结构的非界面自由度和界面自由度；fj为边界作用力。因为子结构作自由振动，所以非界面力为零。

由式（1）和式（2）可得：

B为布尔矩阵，表征了界面自由度在总体自由度中的位置。

求解式（1）可得子结构的正则化模态φr，取前k阶作为子结构的保留主模态φk。设子结构的高阶假设模态为Ψd，即

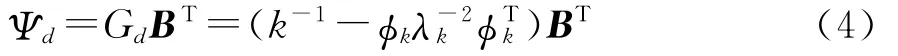
将子结构的保留模态集和剩余模态集组装成假设模态矩阵为：

利用假设模态矩阵，将子结构的物理坐标x转换为模态坐标p，即

pk为选择的低阶保留主坐标；fj为界面力，这里将其作为一组广义坐标。式（6）即为模态综合的第1次坐标变换。将式（6）代入式（1），得子结构在模态坐标下的动力学方程为：

1.2 综合求解

不失一般性，以2个子结构（α和β）为例进行综合。对子结构分别建立模态坐标下的动力学方程，并联立起来，得到系统的自由振动方程为：

假设子结构α和β间只有1个对接界面。引入面力平衡条件αfj＝－βfj，得：

再利用对接面位移协调αxj＝βxj进行装配。联立式（6），将界面力fj表示为保留模态坐标pk的函数形式为：

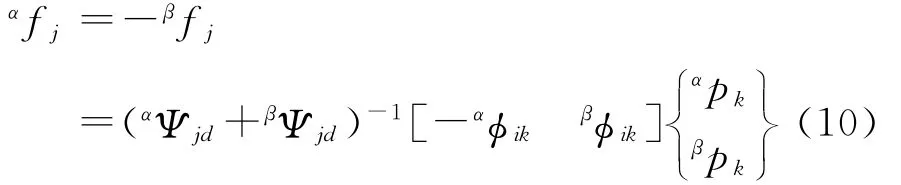
因此，有

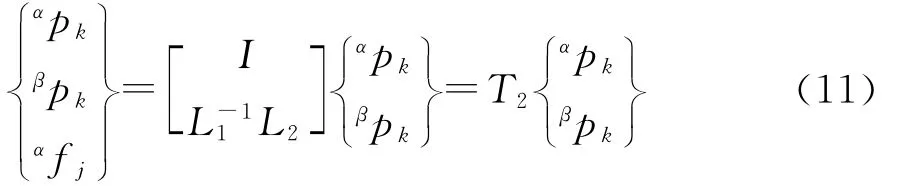
L1＝αΨjd＋βΨjd；L2＝［－αφikβφik］。联立式（9）和式（11）得：

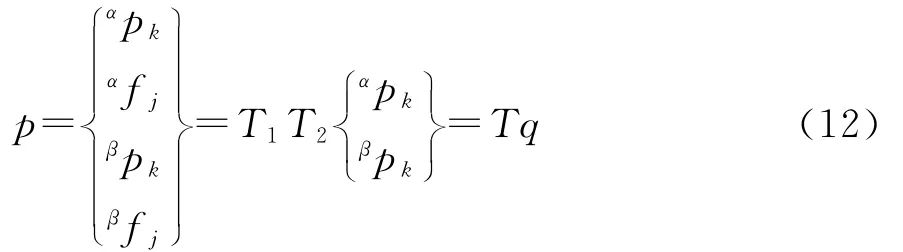
T＝T1T2；q＝［αpLβpL］T。利用式（12），对式（8）进行坐标变换，从而建立解耦后的系统动力学方程为：

求解式（13）可得到系统的固有频率以及系统在广义坐标q下的振型，结合式（6）和式（12）可将结果返回到物理坐标上。例如对于子结构α，有：

αB＝［αIβ0］，它表征了子结构α 的模态坐标αp在p中的位置。

2 刚体模态及弹性连接的处理

对于有刚体模态的自由子结构而言，其刚度阵是奇异矩阵，无法运用式（4）计算剩余柔度。对于这种情况，可以利用移频法［8］来消除子结构刚度阵的奇异性，仍然采用子结构的剩余模态来近似高阶截断模态。移频法的基本公式为：

子结构的综合需要将边界位移协调作为条件来建立第2次坐标变换的转换矩阵。这种假设对于子结构间完全固连的情况较为符合，但是对于连接比较薄弱、变形不连续以及存在连接部件的结构，则不能很好地进行分析。连接子结构的引入可以很好地解决这方面的问题。

连接子结构的基本特征［9］为：仅存在界面自由度而无非界面自由度，所有界面自由度又同时与相邻的模态子结构所共有。其基本特性决定了它的坐标变换矩阵仅仅依赖于相邻子结构模态矩阵中对应于界面自由度的子矩阵，而无法生成独立的广义坐标。设连接子结构的坐标变换矩阵为：

cφ为连接子结构的变换矩阵；αΨjd为α子结构模态矩阵对应于界面自由度的子矩阵；βΨjd为β子结构模态矩阵对应于界面自由度的子矩阵。

3 求解系统的实现流程

3.1 输入模块

输入模块的主要工作是通过收集子结构的模型数据、连接集数以及求解参数来定义模态综合实例。

子结构的模型数据含义：第1部分是指子结构的节点和单元数据，用于实现子结构的显示；第2部分是指子结构的质量矩阵、刚度矩阵以及低阶模态，用于实现子结构的降阶。系统通过文件预处理将bdf文件转换成mdl文件以读取子结构的有限元模型，子结构的质量阵、刚度阵和模态矩阵则可以通过Nastran的SOL103序列（模态分析求解序列）获得。因此，对于理论模型，必须提供子结构的bdf文件，若提供的是其他格式的模型文件，则需要通过相应的软件转换为bdf文件格式。

连接集数据是指子结构之间相互连接的自由度集合以及连接属性。自由度集合包含连接节点编号以及自由度号。连接属性则分为刚性连接和弹性连接，对于弹性连接需要定义各个连接自由度之间的等效刚度，为连接子结构的定义提供必要的数据。

求解参数主要包括：各个子结构的保留模态阶数（各子结构的保留模态数可以不同）、移频量和综合结果的计算阶数。

3.2 子结构降阶模块

子结构降阶模块的作用是处理输入模块读入的信息，为之后的综合求解准备必要的数据。其中，子结构预处理是在子结构与子结构、子结构与连接集之间建立对应关系，并为第2次坐标变换矩阵的子矩阵T1的生成做准备。子结构降阶则是以子结构的bdf文件为基础，通过USET1命令将相应的连接集信息写入bdf文件，然后利用DMAP语言结合求解参数修改SL103序列以实现子结构的降阶，具体的DMAP实现流程如图1所示。

首先，通过MODUSET模块将子结构的分析自由度集划分为界面自由度集和非界面自由度集，然后分别利用UPARTN和MERGE，将子结构的质量阵和刚度阵和模态矩阵按照不同的自由度集进行分块和再组装。对于有刚体模态的子结构，需要使用ADD模块完成移频处理，以消除刚度矩阵的奇异性。在完成系统矩阵的处理后，利用PARTN模块截取保留主模态，然后运用SMPYAD，SOLVE和ADD模块求出剩余模态矩阵，再通过MERGE模块将保留主模态和剩余模态组装成假设模态矩阵。最后，利用SMPYAD模块求出子结构的模态质量阵和模态刚度阵，并通过OUTPUT4模块将模态质量阵和模态刚度阵以及假设模态矩阵输出到op4文件。

图1 子结构降阶流程

对于存在柔性连接的综合实例，需要通过连接子结构模块来构造连接子结构的质量阵和刚度阵。这一过程在VC＋＋程序中完成，并未涉及DMAP程序，故在此不作详细介绍。

3.3 综合求解模块

综合求解模块以SOL100序列为基础，自定义一个新的求解序列，它的输入包括各个子结构的输出、连接子结构的系统矩阵以及第2次坐标变换矩阵的子矩阵T1矩阵。综合求解模块的DMAP流程如图2所示。

通过INPUTT4模块将各个子结构输出到op4文件中的模态质量阵、模态刚度阵以及假设模态矩阵，并读入到求解序列中，T1矩阵的读入则是由DMIIN模块完成。利用ADD模块和MERGE模块分别将求出L1矩阵和L2矩阵，并通过SOLVE模块和MERGE模块构造T2矩阵。使用MPYAD模块将T1和T2相乘得到模态综合第2次坐标变换的变换矩阵T矩阵。得到T矩阵后，利用SMPYAD对综合系统的质量阵和刚度阵进行坐标变换，并用READ模块求出综合系统的特征值、固有频率和振型。最后使用MPYAD模块，将综合系统的振型转化成子结构在物理坐标下的振型，并利用MATPCH模块将结果输出到相应子结构的pch文件中。综合系统的特征值和固有频率频率则通过OFP模块输出到f06文件中。综合求解结束后，通过后处理模块将综合求解模块输出的固有频率和振型读取到内存中，并为每个子结构生成相应rsl文件，以便系统进行读取和显示。

所开发的自由界面模态综合法求解系统是以实验室所开发的混合建模求解系统为基础，该系统的逻辑结构以及数据结构见参考文献［10－12］。

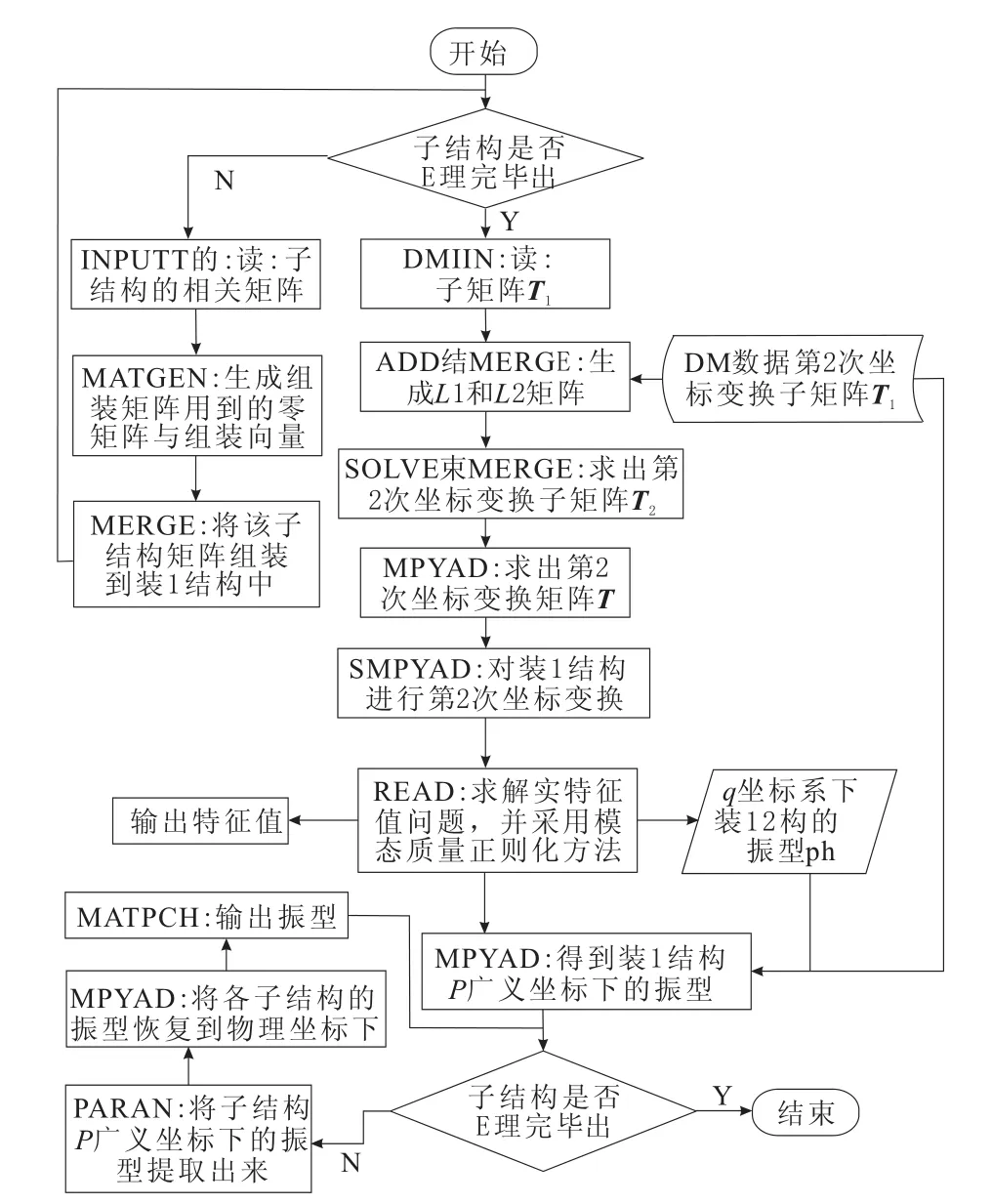
图2 综合求解流程

4 算例验证

4.1 浮筏装置

图3所示为1个浮筏装置的简化机构。其中，m1和m2表示被隔振机械，质量分别为：m1＝200 kg，m2＝250kg，筏架和基座的尺寸分别为：1 200 mm×800mm×20mm和2 000mm×800mm×40 mm。基座的两短边约束、两长边自由，而筏架的四边均自由。筏架和基座的材料参数为：E＝2.0×1011N／m2，ρ＝7 800kg／m3，μ＝0.3。m1和 m2分别通过1个弹簧和阻尼器与筏架相连，筏架通过8个弹簧固定在基座上。将其划分为基座和筏架（含机器）2个子结构。基座与筏架之间的弹簧作为连接子结构，连接子结构的弹簧刚度为k2＝500N／m。基座与筏架之间的弹簧仅存在Y方向的自由度，因此，仅需设置Y方向的连接自由度。又因为子结构2包含有刚体模态，因此，需要对子结构做移频处理，移频量设为1。

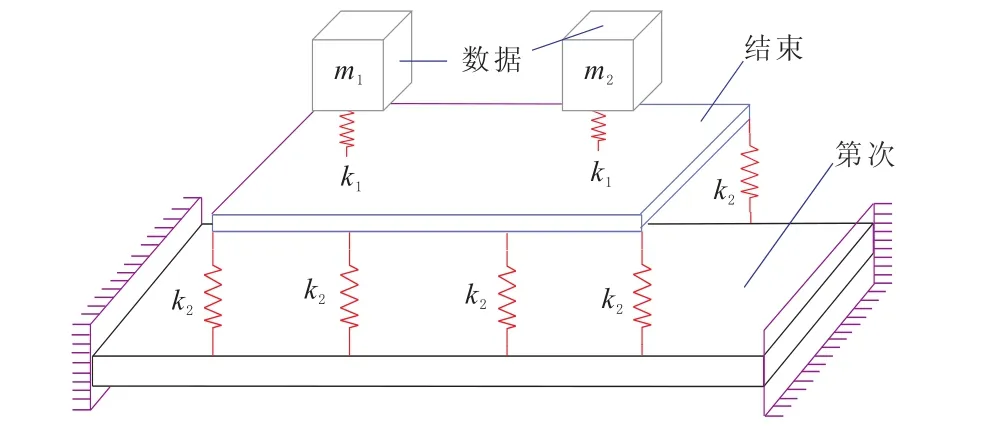
图3 浮筏装置结构

每个子结构选取保留模态为13阶（包含3阶刚体模态）。将模态综合计算结果中的前5阶弹性频率与Nastran整体计算的前5阶弹性频率进行比较，比较结果如表1所示。对比结果表明，系统对弹性连接子结构的综合计算结果能满足工程要求。

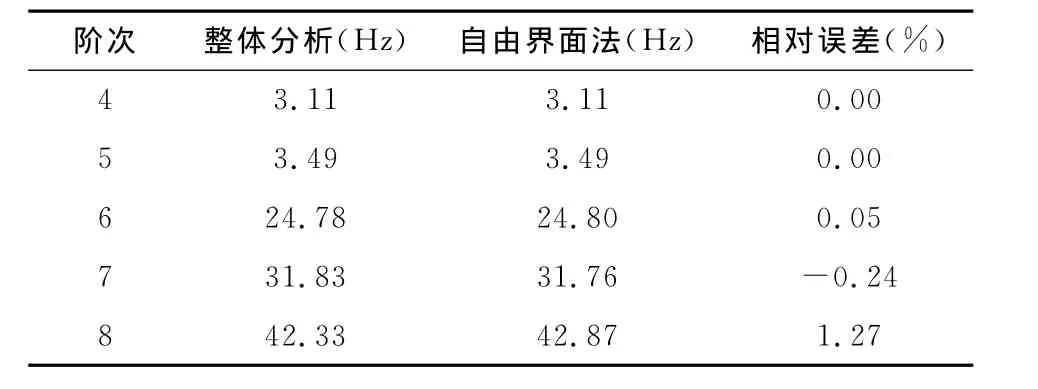
表1 浮筏装置模态综合弹性频率对比

4.2 多子结构及刚性连接验证

以一个飞机模型为例来验证多个子结构件刚性相接的综合计算。将其划分为3个子结构，即机身和2个机翼。飞机模型子结构组装后的整体模型包含19 191个壳单元，18 930个节点，材料参数为：E＝2.0×109N／m2，ρ＝1 750kg／m3，μ＝0.3。子结构之间为刚性连接，每个子结构均取16阶保留模态（包括6阶刚体模态）参与综合，连接自由度为全部6个自由度，移频量设为1。表2为综合分析与整体分析的前5阶弹性频率的对比结果。对比结果表明，该系统对刚性连接子结构的综合计算结果能够满足工程要求。