基于ESO和BESO连续体结构拓扑优化分析
2014-09-06,
,
(长春工业大学机电工程学院,吉林 长春 130012)
基于ESO和BESO连续体结构拓扑优化分析
母德强,范以撒
(长春工业大学机电工程学院,吉林 长春 130012)
使用APDL参数化设计语言编写程序,利用ANSYS软件平台实现了对大型龙门工程机械横梁的拓扑优化。分析结果表明,双向渐进结构优化算法(BESO)迭代过程快,计算效率高,优化结构清晰。
连续体结构;拓扑优化;算法;参数化设计语言
0 引言
渐进结构优化法ESO[1-2]是近年来兴起的一种解决各类结构优化问题的数值方法。通过删除结构中的低效或者无效材料,以使结构“进化”为最优形态[3]。借助现有的有限元分析软件,ESO方法可以方便地解决各种优化问题。在迭代过程中,传统的ESO法删除一些单元后,导致材料的性能不能完全发挥;也可能造成结构的“奇异”而使求解困难。
双向渐进结构优化法BESO[4]是对ESO算法的延伸和改进,可以有效解决ESO方法存在的问题,优化的核心是删除低应力或无应力单元的同时,在高应力单元周围增加新单元,提高材料的使用效率。由于可以逐渐增加结构中所需的材料,所以初始优化区域可以小于设计区域,这就提高了计算效率。
1 拓扑优化方法的发展
[5]主要解决连续体结构的拓扑优化问题,研究了ESO法在频率约束下的有关问题。Chu发表了基于位移约束的ESO的相关研究,由于ESO算法思想简单,可以借助有限元分析软件实现迭代过程,通用性较好。
Querin进一步发展了ESO法,提出不仅可以在迭代中删除低效率的材料,还可以在高应力单元周围增加单元。Yang利用位移优化模型和频率优化模型,介绍了BESO法在解决拓扑优化问题的优势[6]。它在连续体结构拓扑优化的工程应用方面具有宽广的发展空间。
2 拓扑优化方法理论及算法实现
2.1 ESO方法理论与算法实现
ESO方法的基本思想是通过将无效或低效的单元逐步去掉,结构将逐步趋于优化。在优化迭代中,有限元网络是固定的,对存在的材料单元编号为非零数,对不存在的材料单元编号为零。ESO算法的实现过程和BESO优化算法的实现过程前4步是一样的,可见下一节。
2.2 BESO方法理论与算法实现
优化过程中,删除低应力单元的同时,在可能导致结构“奇异”的单元周围增加单元,以确保迭代收敛到最优解,结构保持不变性,充分发挥材料的性能。BESO算法实现的步骤,即
a.在给定的荷载和边界条件下,定义初始设计区域,并用有限元网格离散该区域。
b.在复杂应力条件下,使用Von Mises作为最常用的判别准则,Von Mises应力为:

(1)
σx,σy,σz为正应力;τxy,τyz,τzx为切应力。
c.在每次有限元分析完成后,从模型中删除符合下列条件的所有单元,即

(2)
RRI为当前的删除率,通常取1%~2%。若两应力的比值大于RRI,则认为单元特性处于高应力状态,如果小于RRI,则认为单元特性处于低应力状态,可以删除。
d.重复迭代操作,直至达到下一个稳态。引进一个进化率ER,并把它加到删除率中,即
RRI+1=RRI+ER
(3)
e.每次迭代根据删除率,单元删除个数记为E1。如果删除单元后存在奇异的单元,也一起删除,单元删除个数记为E2。每迭代1次删除单元总数为:
E=E1+E2
(4)
f.检查结构中需要添加单元的节点,增加单元总数为M。
g.在当前迭代过程中,当删除的单元个数N和增加的单元个数M接近时,达到一个稳定状态。
h.增加的删除率重复步骤b~步骤g,直到达到结构的最优拓扑形状。
3 连续体结构优化算法的实现及分析
对有限元软件ANSYS的APDL语言进行二次开发,分别实现了渐进结构优化和双向渐进结构优化算法。
基于这2种方法,对某类大型龙门矿山机械的横梁截面进行拓扑优化设计。初始删除率为0.02,进化率为0.01,体积删除率为50%,过滤半径为0.3,最大迭代次数为200,优化初始模型截面尺寸为10m×2m,如图1所示。弹性模量取2.0×1011MPa,泊松比取0.3,F=2000N。
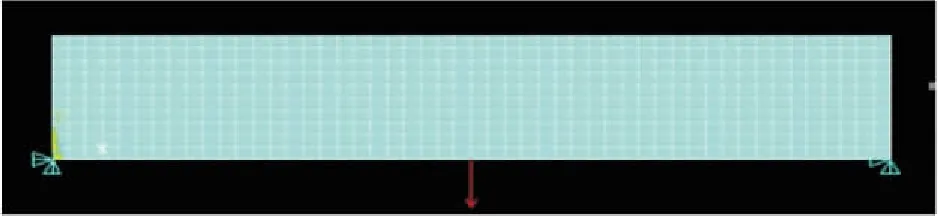
图1 横梁截面结构的有限元模型
图1是横梁截面结构的有限元模型,在结构的左右节点施加完全约束,结构中点位置受一个集中载荷力F。图2是使用ESO算法进行拓扑优化的结果,由图2可知,一些单元被删除后,不能恢复,这样就造成了最终优化结果上一些单元的缺失,不但影响优化的美观,对后续的提取结构模型进行圆整增加困难。图3是使用BESO算法进行拓扑优化的结果,由图3可知,图形结果非常清晰,优化结果新颖,为下一步的提取模型,生产实体进行形状优化和多目标优化提供更大的方便。

图2 ESO拓扑优化模型

图3 BESO拓扑优化模型
2种算法的体积删除率和迭代过程如图4所示。横轴代表优化迭代的次数;纵轴体积分数表示的是在整个优化迭代的过程中,体积的减小百分比,随着迭代过程的进行,体积逐渐减小至不变;纵轴平均柔度(N·mm)是整个结构的平均柔度大小,随着迭代次数的增加,结构的平均柔度趋于稳定,它反映的是结构单元的承载刚度。由图4知,经过30步的迭代,结构的体积达到平衡状态。结构的设计过程中刚度是一个重要的影响因素。通常,在最大的变形量的约束下要求有最大的刚度。而且,拓扑优化就是在最大的刚度和规定体积下寻找材料的最好布置方式。在此过程中,使用应变能去衡量结构的最大刚度,最大刚度也代表着结构的平均柔度。所以,图4a最终平均柔度是3.5×10-7N·mm,图4b最终的平均柔度是4×10-7N·mm。单元的平均柔度越高,这说明结构材料性能得到了充分的体现,高效单元更多,低效或无效单元更少。优化的结果证明了BESO优化算法的优点。
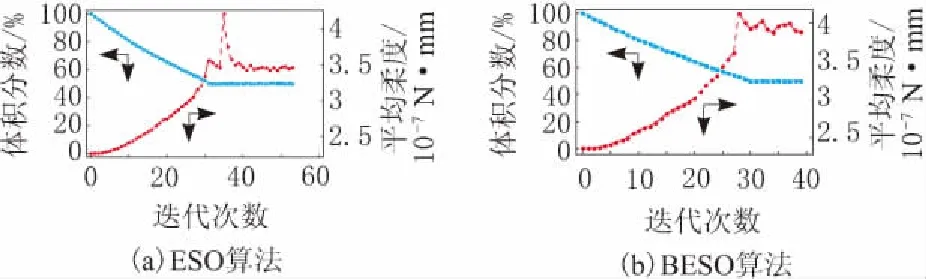
图4 体积删除率和迭代过程变化
4 结束语
对有限元软件ANSYS的APDL语言进行二次开发,分别实现了渐进结构优化和双向渐进结构优化算法。分析结果表明,BESO比传统的ESO算法具有更好的优化性能,验证了BESO的正确性和有效性。
参考文献:
[1] 荣见华,谢忆民,姜节胜,等.渐进结构优化设计的现状与进展[J].长沙交通学院学报,2001,17(3):17-24.
[2] Xie Y M,Steven G P.Shape and layout optimization via an evolutionary procedure[C].Proceedings of the International Conference on Computational Engineering Science,Hong Kong,1992.
[3] 谢亿民,黄晓东,左志豪,等.渐进结构优化法(ESO)和双向渐进结构优化法(BESO)的近期发展[J].力学进展,2011,41(4):462-471.
[4] Yang X Y,Xie Y M,Steven G P,et al.Bidirectional evolutionary method for stiffness optimization[J].AIAA Journal,1999,37(11):1483-1488.
[5] Xie Y M,Steven G P.Evolutionary structural optimization[M].Berlin,Heidelberg,New York:Springer-Verlag Berlin and Heidelberg GmbH & Co.K,1997.
[6] Yang X Y,Xie Y M,Steven G P.Evolutionary methods for topology optimization of continuous structures with design dependent loads[J].Computers & Structures,2005,83(12):956-963.
Topology Optimization Analysis Based on ESO and BESO Continuum Structures
MUDe-qiang,FANYi-sa
(School of Mechatronic Engineering,Changchun University of Technology,Changchun 130012,China)
In this paper,writing programs by ansys parametric design language (APDL),and using ANSYS software platform we completed the topology optimization process of large-scale project machinery beam gantry.The results show that,BESO algorithm has advantages of fast iterative process,high computational efficiency and clear optimize structure.
continuum structure;topological optimization;algorithm;parametric design language
2013-12-27
TH122
A
1001-2257(2014)06-0076-02
母德强(1961-),男,辽宁昌图人,教授,博士研究生导师,院长,研究方向机械系统动力学与优化设计;范以撒(1986-),男,河南周口人,硕士研究生,研究方向数字化设计与分析技术。
