加氢裂化工艺操作过程的优化分析

杨东奎，王 阔，王继锋

(1.辽宁石油化工大学，辽宁 抚顺 113001；2.中国石化抚顺石油化工研究院)

加氢裂化工艺操作过程的优化分析

杨东奎，王 阔2，王继锋2

(1.辽宁石油化工大学，辽宁 抚顺 113001；2.中国石化抚顺石油化工研究院)

通过样条曲线插值的数学方法，建立了加氢裂化反应过程中的处理量、温度对裂化产品物化性质影响的数值模型，并将该模型应用于减压蜡油(VGO)的加氢裂化工艺优化分析。该优化问题以VGO加氢裂化反应的处理量和温度为变量，以产品中喷气燃料馏分的烟点、冰点，柴油馏分收率以及中油选择性作为约束条件，考察在上述约束条件下工艺操作参数的可行区间，并在此相关条件约束下，基于所确立的数学模型计算相关转化率的最小值，以便获得系统高产尾油时的工艺操作参数，并与实验数据进行对比。对比结果表明，该方法效果良好，所得数据与实验数据相近。

加氢裂化 工艺参数 样条曲线 优化分析 减压蜡油 约束条件

工艺运转评价对催化剂的开发以及相关催化反应过程的评估与优化有着不可替代的作用，是催化剂研发的必要组成部分，因此，研究人员对此进行了大量的研究，并取得了一定的成果[1-2]。然而，由于催化工业过程极其复杂，目前对于工艺运转试验的设计以及运转数据的后处理仍然存在很大的局限性，具体表现在：现阶段的工艺评价对于各类油品参数与各类工艺条件的“综合”依赖关系几乎没有一个较为全面的定量认识；对于实验所采集的数据缺乏必要而有效的处理，在已有数据与各类工艺条件的关联以及已有数据自身关联性的有效挖掘方面所做的工作更少；对于各类催化剂的相关工艺所做的优化工作多停留在“经验阶段”，没有必要的黑箱[3]唯象理论和算法予以支持。

现阶段对于加氢裂化工艺优化问题的研究仍面临相当大的困难。首先，要确立一种较为准确的成品油性能与运转工艺条件的高维显式函数关系十分困难。传统的函数确立方法是最小二乘法[4]，然而，该方法必须首先确立相关函数的结构，再根据已确立的函数结构使用参数估计的方法计算相关函数的参数，其中最为困难的部分是函数结构的确立，而文献报道大多为函数结构优先确立的情况[5]。其次，成品油性能对运转工艺条件的函数属于多参数函数模型，其数据空间呈现超曲面性状，往往超出人们的想象能力，这更为函数表达式的合理选择增加了难度。另外，即使相对准确地确立了所需的各类近似描述工艺过程的函数，各类函数的自身复杂性也对传统的最优化方法提出了巨大的挑战[6]，现实中的优化体系往往具有极大的非凸性和极强的非线性特征[7]，这也为优化问题的数学求解带来阻力。

为了避开传统数学方法解决实际问题的不足，本研究采用样条曲线的数学方法，并基于具体实验数据，采用分片插值的方法来描述特定催化剂作用下减压蜡油(VGO)标准原料油加氢裂化的工艺优化问题。

1 实 验

实验在60 mL小型加氢装置上进行。原料为伊朗VGO，按照实验设计的需要不断调整实验温度及处理量，且在不同工艺条件下采集产品。产品以小于82 ℃馏分为轻石脑油馏分、82～132 ℃馏分作为重石脑油馏分、132～282 ℃馏分作为喷气燃料馏分、282～370 ℃馏分作为柴油馏分、大于370 ℃馏分作为尾油馏分，并以喷气燃料和柴油馏分的加和作为中油馏分。通过对馏分切割数据的采集以及对采集的实验数据进行数值样条插值计算，即可获得各馏分的含量。

2 数值模型的建立

Matlab工具包中的griddata函数[8]可以将位于同一空间坐标系下的散点插值为规则格网，并提供包括基于Delaunay三角形的线性插值、三次多项式插值及最近点插值等数值方法，可以方便地实现结合邻近离散点分布特征的光滑曲面拟合。

本研究只有温度和处理量两个变量参数，可以采用二元样条函数来处理。样条函数[9]是满足一定连续条件的分片插值多项式，具有简单性和协调性的优点，可利用meshgrid函数在二维空间内将温度、处理量的实验数据张成一个四边形格网，然后在这些格网内做三角剖分，在三角形内部采用面积坐标计算相关油品性质，再将相同油品性质对应的工艺操作点连接成线，即为操作条件等势线。根据此方法可分别做出轻石脑油收率、重石脑油收率、柴油收率、转化率等的等势线。

通过编写Matlab命令文件，即可在Matlab环境下实现相关计算，并通过Matlab的图形可视化功能，得到所需的数值模型。

3 结果与讨论

3.1 生成油特征参数的计算与收集

分别将不同加氢裂化工艺条件下得到的生成油采用5 L实沸点蒸馏装置进行馏分切割，所得结果见表1。由表1可见，裂化反应转化率与中油选择性之间存在着此消彼长的关系。

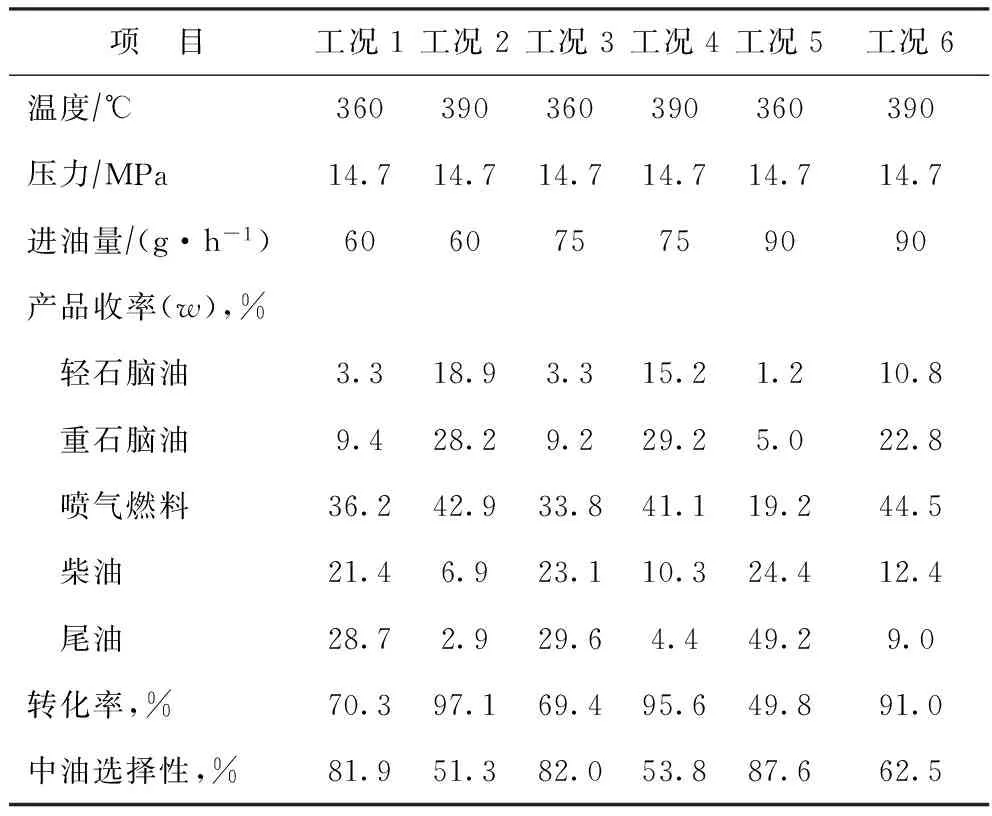
表1 部分生成油的馏分切割数据

3.2 生成油特征参数对工艺条件的等势线图绘制

分别将表1中的生成油切割数据对加氢裂化工艺条件(包括温度和处理量)做二维等势线图，结果见图1。由图1可见：原料转化率随温度的增加和处理量的降低而增加；产品的中油选择性随温度的增加及处理量的降低而降低，其变化趋势与转化率相反；产品中轻、重石脑油馏分收率随温度的增加和处理量的降低而增加，其增加速率在处理量较低时受温度的影响较为显著。产品中柴油馏分收率随温度的增加而降低，但随处理量的增加而先增加后降低，这是因为在较低的反应温度下原料油裂化生成柴油馏分的反应要比柴油馏分进一步生成其它馏分的反应更容易，而提高反应温度则加剧了柴油的二次裂化反应，致使柴油馏分更多地裂解为喷气燃料或更轻的馏分，故其收率有所降低[10]；当处理量较低时，尾油馏分裂解为柴油馏分的速率大于柴油馏分裂解的速率，以至于柴油馏分累计增加；当处理量较高时，尾油馏分裂解为柴油馏分的速率小于柴油馏分裂解的速率，从而使柴油馏分逐渐减少。产品中的喷气燃料馏分收率变化较为复杂，当处理量较高时，产品中的尾油和柴油馏分含量较高，可以不断转化为喷气燃料馏分，且其转化速率大于喷气燃料的裂解速率，故随温度的增加，喷气燃料收率不断增加；而当处理量较低时，产品中的尾油和柴油馏分含量较低，已经无法提供足够的馏分来转化为喷气燃料馏分，与此同时，喷气燃料的裂解速率却随着温度的增加而增加，这就导致喷气燃料收率随温度增加而先增加后减小。绝大多数生成油馏分的收率均表现出与裂化反应工艺条件较强的非线性依赖关系。

3.3 喷气燃料馏分特征参数对相关工艺条件的等势线图绘制

依据喷气燃料数据分别将喷气燃料馏分的冰点、烟点、萘系烃含量、芳烃含量对加氢裂化工艺条件做二维等势线图，结果见图2。由图2可见：喷气燃料产品的冰点近似随反应温度的增加而降低，随处理量的降低而增加，但当处理量较大时，其随处理量变化不大，故在高温和低处理量的工况条件下生产的喷气燃料低温性能较好；喷气燃料的烟点和芳烃含量随反应温度的增加分别增加和降低，随处理量的增加分别降低和增加，但当处理量较大时，两种性质变化却不大；喷气燃料烟点及芳烃含量对工艺条件等势线的变化形态较为相似，但其数量的变化却呈近似相反的规律，这可能是由于烟点的变化反映喷气燃料燃烧积炭倾向的变化趋势，喷气燃料中芳烃含量越高，烟点就越低；喷气燃料的萘系烃含量随反应温度的增加而降低，但随处理量的增加呈先增加后降低的趋势，在处理量较低时，其变化趋势完全类似于喷气燃料的烟点及芳烃含量。

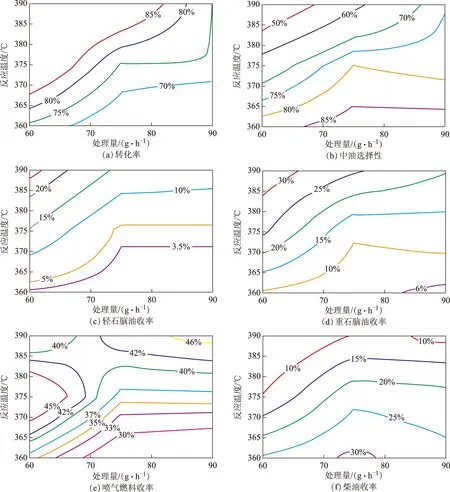
图1 生成油特征参数对工艺条件的等势线图

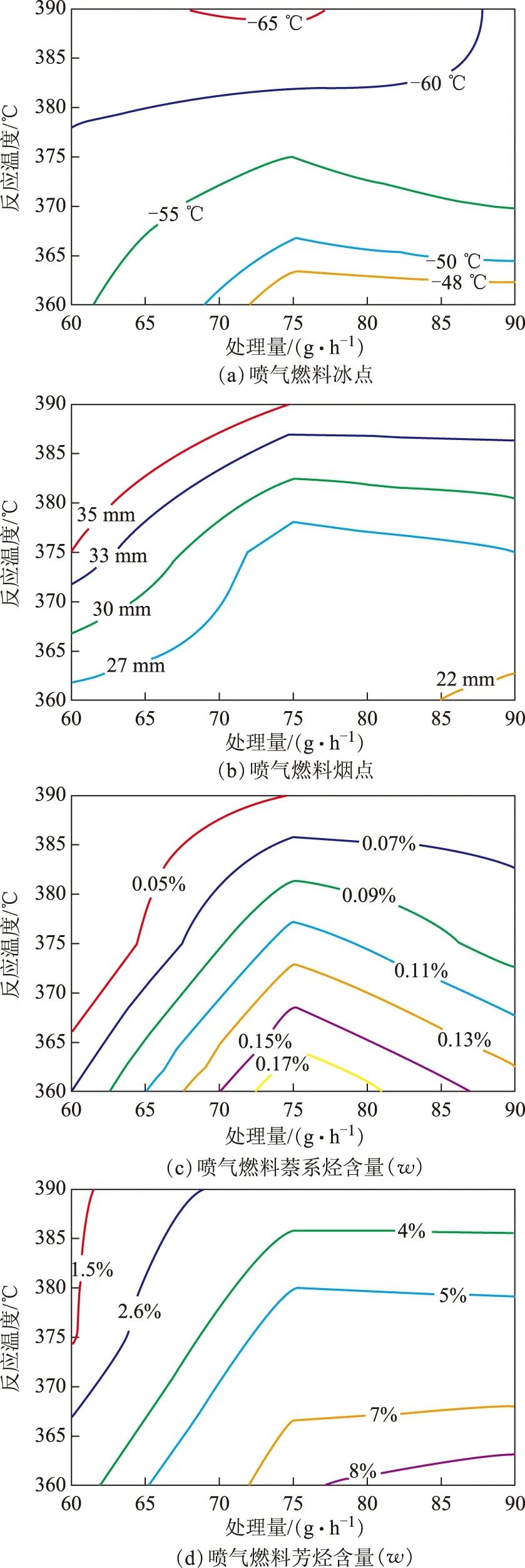
图2 喷气燃料特征参数对工艺条件的等势线图

3.4 加氢裂化工艺的优化分析

在实际加氢裂化工艺操作过程中，一般要求在指定产品性质的约束下来调整加氢裂化反应工艺条件。然而，满足指定产品性质要求时所对应的工艺条件涉及的操作区间可能较为复杂，甚至所涉及的可行工艺操作点可能不存在，可能存在且唯一，也可能有多个，因此，这就牵涉到最优工艺点的选择问题。

3.4.1 复合工艺优化操作区间的确立 在实际生产操作过程中，对产品某种性质的要求可能并不唯一，可能会根据市场的需要以及上下游工况而对各馏分油产品的性质提出不同要求。现有的工作很少将如此复杂的产品质量与工艺操作要求考虑在一起分析，一般仅用单工艺条件优化[11]的方法分别进行讨论，这将在相关计算过程中无法满足需要，因此，在此选择多种因素复合考察的研究方法。假设对馏分油的相关性质要求如下：喷气燃料冰点：大于-52 ℃，喷气燃料烟点：22～25 mm，中油收率：大于83%，柴油收率：大于25%。分别绘制在各类产品性质约束下对应的工艺操作区间，结果见图3。

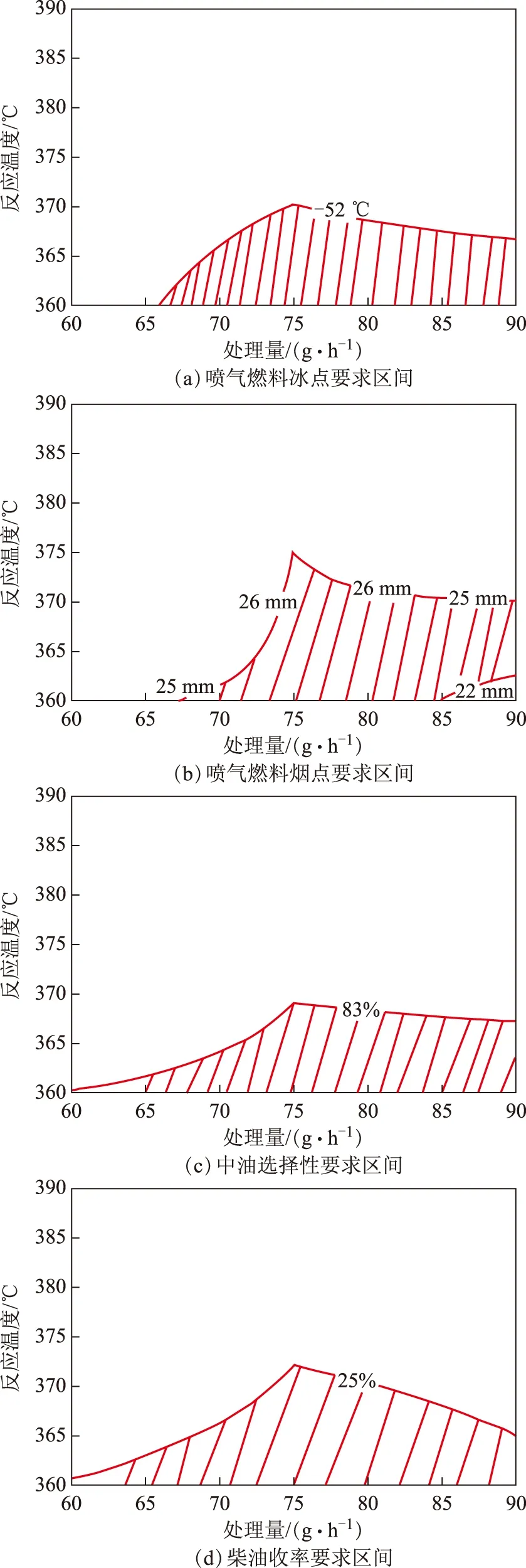
图3 满足各类产品性质要求时对应的工艺操作区间

假定喷气燃料冰点、喷气燃料烟点、中油选择性以及柴油收率所确立的工艺操作区间分别为Ω1，Ω2，Ω3，Ω4。根据约束条件的逻辑关系及操作参数空间的几何关系，可以确定符合约束条件的操作空间在逻辑上满足式(1)。

Ω可行=Ω1∩Ω2∩Ω3∩Ω4

(1)

将所涉及的各类等势线绘制在同一张图上，如图4所示。复合工艺优化问题的实际可行工艺区间即为图3所描述的4类工艺操作区间在几何上的交集，其相关的复合工艺操作区间如图5所示。由图5可见：复合工艺操作区间带有一定的任意性，形状极不规则；复合工艺操作区间由4类油品性质约束条件共同确立，不同的约束条件联合确立可行工艺操作区间的边界；复合工艺操作区间不是数学上典型的凸区间，不能用传统函数[12]的求解方法来计算，因此在该区间上进行的优化可能较为复杂，可对其进行剖分再采用传统优化方法计算，也可将复合工艺操作区间视作一个整体而采用近现代软计算[13-17]方法进行计算。

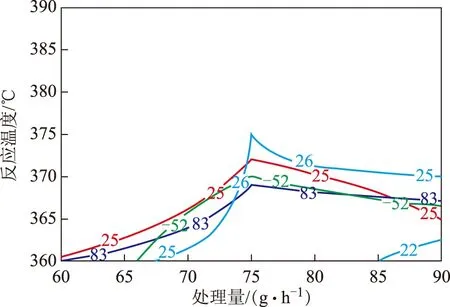
图4 各类产品性质的等势线图 —喷气燃料冰点/℃; —喷气燃料烟点/mm; —中油选择性，%; —柴油收率，%

图5 复合工艺优化问题所对应的操作区间 —喷气燃料冰点/℃; —喷气燃料烟点/mm; —中油选择性，%; —柴油收率，%

3.4.2 复合工艺操作区间上的转化率优化分析在满足以上操作区间区域范围的前提下，为最大限度地生产尾油，也就是使裂化反应在该约束条件下的转化率达到极小值，将以上要求表达为标准的数学形式：Min转化率，S.T.喷气燃料冰点：大于-52 ℃，喷气燃料烟点：22～25 mm，中油选择性：大于83%，柴油收率：大于25%。

基于上述目标函数及约束条件，分别绘制复合工艺操作区间及转化率的等势线，如图6所示。图6中几条不同颜色的实线分别代表各类性质等势线，虚线则代表转化率等势线。通过对转化率等势线与相应操作区间相对位置的观察，可以得到：转化率随温度的增加及处理量的降低而增加。图6中，等势线由右下角向左上角呈非线性增加，在等势线簇由右下角向左上角推进的过程中逐渐接近所需的工艺操作区间，然后与之相交，最后再离开所需工艺操作区间；在操作区间范围内，转化率的最小值所对应的处理量约为85 g/h，而对应的裂化反应温度约为360 ℃，其限制条件的瓶颈在于喷气燃料的烟点要求；在操作区间范围内，转化率的最大值所对应的处理量约为75 g/h，而对应的裂化反应温度约为370 ℃，其限制条件的瓶颈在于中油选择性的要求。

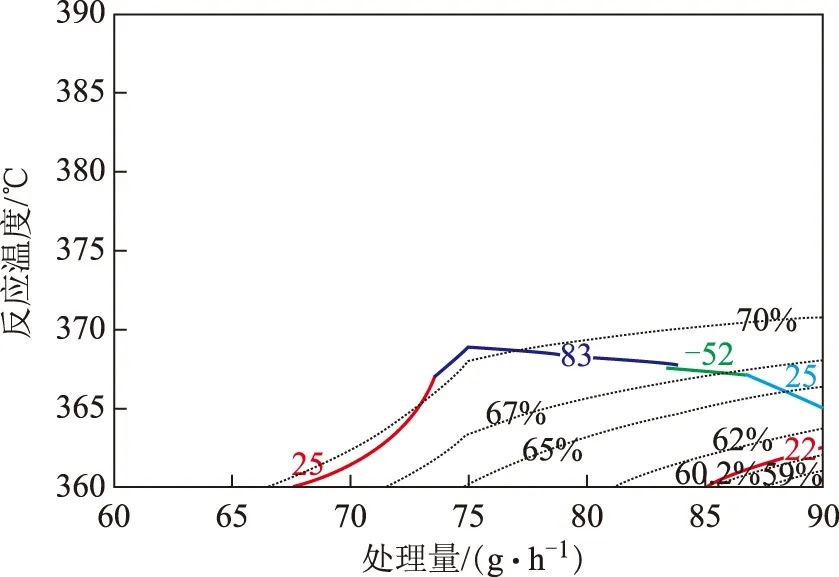
图6 复合工艺优化问题所对应的操作区间及转化率等势线图 —喷气燃料冰点/℃; —喷气燃料烟点/mm; —中油选择性，%; —柴油收率，%

按照相关的计算结果，分别将裂化段工艺条件设置为：压力14.7 MPa，处理量85 g/h，反应温度360 ℃。在此条件下的产品性质见表2。由表2可见，所估算的产品性质与实际产品性质相近，馏分油转化率的误差仅为0.27%左右，说明此方法具有良好的优化效果。

表2 产品性质估算值与实际值对比

4 结 论

为了解决加氢裂化工艺过程中复杂工艺操作区间的确立及工艺操作点的优化问题，设计了产品切割方案，基于实验数据以及样条曲线插值的数学思想，建立了在各种工艺约束条件下的特征参数模型，并基于该模型绘制特征参数对工艺条件的等势线图，考察了裂化温度和处理量对转化率、中油选择性、柴油收率以及喷气燃料的收率、冰点、烟点等的影响，同时将该种建模方法和分析方法应用于特定催化剂作用下VGO加氢裂化工艺优化的研究，并考察了在各种复杂约束条件下，加氢裂化工艺的最优化操作区间及其相关转化率的极值问题。该方法方便、便捷、可靠、高效，克服了传统最优化方法的诸多不足，为寻找最优化工艺操作点提供了最佳方案，并对油品炼化工艺中其它各种优化问题的分析和研究具有借鉴意义。

[1] 张会成，颜涌捷，赵荣林，等.渣油加氢处理过程中金属分布与脱除规律的研究[J].石油炼制与化工，2006，37(11)：7-10

[2] 韩照明，刘长厚，蒋立敬.固定床渣油加氢过程催化剂级配优化研究及工业应用[J].当代化工，2006，35(5)：333-347

[3] 魏传锋，王浚.黑箱建模方法在环境模拟实验中的应用[J].航天器环境工程，2005，22(4)：204-206

[4] 王毅敏，马丽英.传统最小二乘法曲线拟合的缺陷及其改进[J].电力学报，1997，12(1)：51-54

[5] 吕翠英，吴江宏，林慧敏.催化裂化反再系统神经网络操作优化[J].计算机与应用化学，2002，19(1)：447-450

[6] 罗述全.传统优化算法与遗传算法的比较[J].湖北工业大学学报，2007，22(3)：32-35

[7] 陈宝林.最优化理论与算法[M].北京：清华大学出版社，1998：341-347

[8] 陈本富，王贵武，沈慧，等.基于Matlab的数据处理方法在GPS高程拟合中的应用[J].昆明理工大学学报(理工版)，2009，34(5)：1-4

[9] 陈娟，李崇君，陈万吉.采用三角形面积坐标的四边形17节点样条单元[J].应用数学和力学，2010，31(1)：117-126

[10]孙忠超，山红红，刘熠斌，等.基于支持向量回归的重油催化裂化产物建模及优化[J].石油炼制与化工，2012，43(5)：76-81

[11]周红军，石铭亮，翁惠新，等.芳烃型催化重整操作条件的分析及优化[J].石油学报(石油加工)，2010，26(2)：257-263

[12]罗娜，钱锋.基于支持向量机的催化剂失活建模方法[J].计算机与应用化学，2008，25(7)：801-804

[13]王华，唐国金.函数优化问题的一种异步并行模拟退火算法[J].控制与决策，2005，20(5)：579-582

[14]孙小平，张双虎.基于并行组合模拟退火的全局优化算法[J].西安理工大学学报，2004，20(4)：396-399

[15]张颖，刘艳秋.软算法方法[M].北京：科学出版社，2002：109-128

[16]曹德铭，袁希钢.产量要求不确定单产品周期间歇过程的最优化[J].计算机与应用化学，2001，18(5)：505-510

[17]罗立，魏关锋，姚平经，等.多流股换热器网络的识别与构造[J].计算机与应用化学，2004，21(3)：333-338

OPTIMIZATION ANALYSIS OF HYDROCRACKING OPERATION

Yang Dongkui1， Wang Kuo2， Wang Jifeng2

(1.LiaoningShihuaUniversity，Fushun，Liaoning113001； 2.FushunResearchInstituteofPetroleumandPetrochemicals，SINOPEC)

A numerical model was established by spline curve interpolation method to study the relationship between physico-chemical properties of the cracking products and the operation parameters of throughput and temperature in hydrocracking process. This model was applied to the optimization analysis of a VGO hydrocracking process. The smoke point and freezing point of aviation jet fuel， diesel yield as well as middle distillate selectivity were used as the constraint objects in the optimization to investigate the feasible operation parameter ranges of throughput and reaction temperature. Under the constraint objects， the minimum conversion was calculated by the model to get the operation parameters for high tail oil yield and compared with the experimental data. The comparison shows that the method has a good effectiveness and the data calculated is close to the experimental results.

hydrocracking； process parameter； spline curve； optimization analysis； VGO； constraint condition

2013-11-25； 修改稿收到日期： 2014-02-27。

杨东奎，硕士研究生，主要从事催化材料及分子模拟方向的研究工作。

王阔，E-mail：kkchemical2006@163.com。

中国石油化工股份有限公司合同项目(113026)。