基于频响函数矩阵计算阻尼系统动力响应的新方法

张 淼， 于 澜 ， 鞠 伟

(1.长春工程学院 理学院，长春 130012；2.中国第一汽车股份有限公司 技术中心，长春 130012)

计算结构动力响应时若采用直接积分法，对于每一个时间步长，其运算次数与半带宽、自由度数的乘积成正比。当半带宽较大且时间历程远大于系统的最小固有振动周期时，结构动力响应的计算将是很耗时的。而振型迭加法在一定条件下可以取得比直接积分法高的计算效率，它主要是利用系统自由振动的模态振型将多自由度的动力方程组转换成为相互解耦的独立方程，对每一个方程可以求解其响应的解析解和数值解。在对每个方程求解时常常采用Duhamel积分法，在一般情况下，它也需要数值积分来计算，只有极少数简单情况才可以得到解析解。直接积分法和振型迭加法各有优势，目前被工程界广泛应用。

对于经典阻尼系统，由于其阻尼矩阵能被系统的无阻尼固有振型对角化，因此可以实现系统解耦，在理论上其响应求解不存在困难，只是在求解每一个解耦方程的过程中，需要考虑所使用的算法的稳定性及计算代价[1]。若将系统转入状态间格式，在状态方程中使用直接积分法，迭代产生响应的近似解序列[2～4]，与其伴随的则是计算精度及计算效率的平衡问题[5]。对于非经典阻尼引起的耦合问题，传统的实模态理论无法使方程解耦。目前常用的计算响应的方法是近似对角化法，但若结构的整体模态阻尼矩阵的某些非对角元数值较大时，直接忽略非对角项所引起的误差的可控性还有待研究[6]；再者是采用复模态解耦方法来计算响应[7]，但计算过程相当复杂。

文献[8]提出了一种函数变换方法，转移系统阻尼项的影响，使用数值技术求解时变矩阵的特征向量，给出了自由振动的响应近似解。文献[9]中利用矩阵分析原理及变换前后系统的振型向量之间的内在联系，给出了系统相应的模态计算方法。由于频率响应矩阵包含的信息丰富，实测方便，测量的精度较高，因此使用频率响应矩阵解决许多工程应用的实际问题，诸如模型修正[10]及结构损伤识别[11-12]等。在这些研究的基础上，本文拟使用矩阵函数变换将阻尼系统转化为无阻尼时变系统，从而既克服了阻尼项所带来的困扰，又更容易求得其模态参数，进而推导并证明了计算其频率响应矩阵的公式，并以此为基础提出了一种基于频响函数矩阵求解经典和非经典阻尼系统精确响应的新方法，结论的公式精确简单，易于实施。本文方法在解决经典阻尼问题时，与振型迭加法同为解析解；对于非经典阻尼系统，无法直接使用振型迭加法解决，而相较于Newmark法，本文方法的最大优势在于它为精确解，而非数值解。

1 多自由度阻尼系统的转化

对自由度为n的阻尼系统，设M、C、K分别是对称的质量、阻尼和刚度矩阵，相应的运动微分方程为:

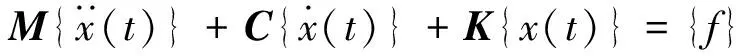
(1)

若取V=[{v1},…,{vn}]为无阻尼正则振型矩阵，则模态质量和模态刚度矩阵变为:

VTMV=diag(m1,m2,…,mn)=I

(2)

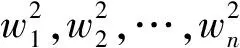
记模态阻尼矩阵为:

(3)

并取坐标变换

{x(t)}=V{q(t)}

(4)

在模态坐标{q(t)}下，式(1)等价于:

(5)

当式(5)中的模态阻尼阵为对角矩阵D=diag(d1,…,dn)时，式(1)称为经典阻尼系统，否则称为非经典阻尼系统。事实上，对经典阻尼系统，式(5)表明，原动力系统已经实现解耦，正如引言中所叙述的那样，可以采用振型迭加法，求解出每个节点处的动力响应。为了得到更加精确的结论，本文提出一种计算阻尼系统精确响应的新方法。为此，定义一个与模态阻尼矩阵有关的矩阵函数变换:

{y(t)}=eDt{q(t)}

(6)

或其逆变换:

{q(t)}=eDt{y(t)}

(7)

则:

(8)

和

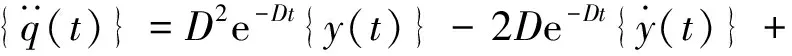
(9)

将式(7)～式(9)代入式(5)得:

(10)

用eDt左乘式(10)两端，有:

(11)

这时式(11)变为无阻尼振动系统的运动微分方程。为了讨论其特征问题，引入状态方程。

2 阻尼系统的复模态分析

对一般动力系统式(1)，把时间域上的矩阵方程变换到以λ为变量的拉氏域中，并假定初始位移和初始速度均为零，则得:

(λ2M+λC+K){X(λ)}={F(λ)}

(12)

令:

Z(λ)=λ2M+λC+K

则:

Z(λ){X(λ)}={F(λ)}

即:

{X(λ)}=H(λ){F(λ)}

式中H(λ)称为传递矩阵。沿频率轴jω计算的传递矩阵称为频率响应矩阵。且:

|Z(λ)|=0

(13)

即为式(1)的特征方程，特征方程的根为式(1)的极点，决定式(1)的共振频率。

为了把式(12)转化为一般特征问题，我们引入恒等式：

(λE-λE){X(λ)}=0

(14)

将式(12)与式(14)相结合得:

(15)

其中:

如果右端向量为零，式(17)就成了关于实值矩阵A的一般特征问题:

(A-λE){Y}={0}

(16)

其特征值满足方程:

|A-λE|=0

(17)

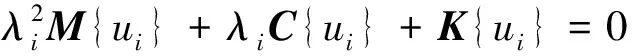
(i=1,2,…,n)

基于上面关于一般动力系统的复模态理论，具体考虑无阻尼系统式(11)的极点和模态振型，并利用它们求系统式(11)的响应。

3 经典阻尼系统的精确响应求解

对经典阻尼系统，系统(1)的模态阻尼矩阵D为对角阵，所以矩阵D2也为对角阵，根据矩阵代数理论，矩阵函数f(D)=diag(f(d1),…,f(dn))也是对角阵，即

(18)

从而无阻尼系统式(11)的系数矩阵便约化为常数对角阵,即

eDt(Λ-D2)e-Dt=Λ-D2

相应地，在坐标变换式(7)下，式(5)等价于:

(19)

即由式(16)可有:

[(D2-Λ)-λ2E]{X}={0}

(20)

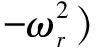
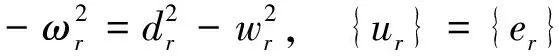
(r=1,2,…,n)

(21)

其中{er}为单位向量。至此求出了系统式(19)的模态参数，就可以利用它们来表示其频响函数。

定理1[13]对阻尼系统(1)，其传递矩阵为:

其中Qr为比例换算因子。

定理2[13]对阻尼系统(1)，其频率响应矩阵为:

其中2jωrmrQr=1，mr为模态质量。

由于系统式(19)的模态向量为单位坐标向量，即VTV=I，且该系统的质量阵为单位阵，因此由定理3可得系统式(19)的频响函数矩阵为对角阵:

(22)

由此，在简谐激励力作用下，当输入力为{f}={F}eiωt时，系统式(19)的稳态响应为:

{y(t)}=H(jω)eDtVT{f}

(23)

再根据式(4)和式(7)，可得原阻尼系统式(1)的响应为:

{x(t)}=Ve-DtH(jω)eDtVT{f}

(24)

根据式(18)及式(22)可知，eDt,e-Dt及H(ω)均为对角阵，所以上式简化为:

{x(t)}=VH(jω)VT{f}

(25)

由式(25)可知只需利用无阻尼正则振型、无阻尼固有频率及模态阻尼矩阵等信息即可求得简谐激励下的任一经典阻尼动力系统的精确响应。

4 非经典阻尼系统的精确响应求解

对非经典阻尼系统，无法直接使用振型迭加法求解，为此本文提出一种基于模态参数求解非经典阻尼精确响应的新方法。

对非经典阻尼系统，模态阻尼矩阵D不是对角阵，对应系统式(11)的状态矩阵A为

与(20)式类似地可有

[eDt(D2-Λ)e-Dt-λ2E]{X}={0}

这是关于矩阵eDt(D2-Λ)e-Dt的特征问题表达式。模态阻尼矩阵D虽不是对角阵，但它为对称阵，因此可正交相似于对角阵，即存在正交阵P，使:

D=Pdiag[k1,…,kn]PT

(26)

根据矩阵代数理论，矩阵函数:

eDt=Pdiag[ek1t,…,eknt]PT

(27)

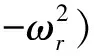
(r=1,2,…,n)

其中{er}为单位向量。由于系统式(11)的模态向量为eDt{er}(r=1,2,…,n)，且该系统的质量阵为单位阵，因此由定理3系统式(11)的频响函数矩阵可简化为对角阵：

(28)

由此，在简谐激励条件下，当输入力为{f}={F}eiωt时，系统式(11)的稳态响应为：

{y(t)}=[H(jω)]eDtVT{f}

(29)

再由式(4)和式(7)可得系统式(1)的稳态响应为：

{x(t)}=Ve-Dt[H(jω)]eDtVT{f}

(30)

其中H(jω)的算法见式(28)， eDt的算法见式(27)。

5 数值算例

作为算例1，考虑如图所示的动力系统。

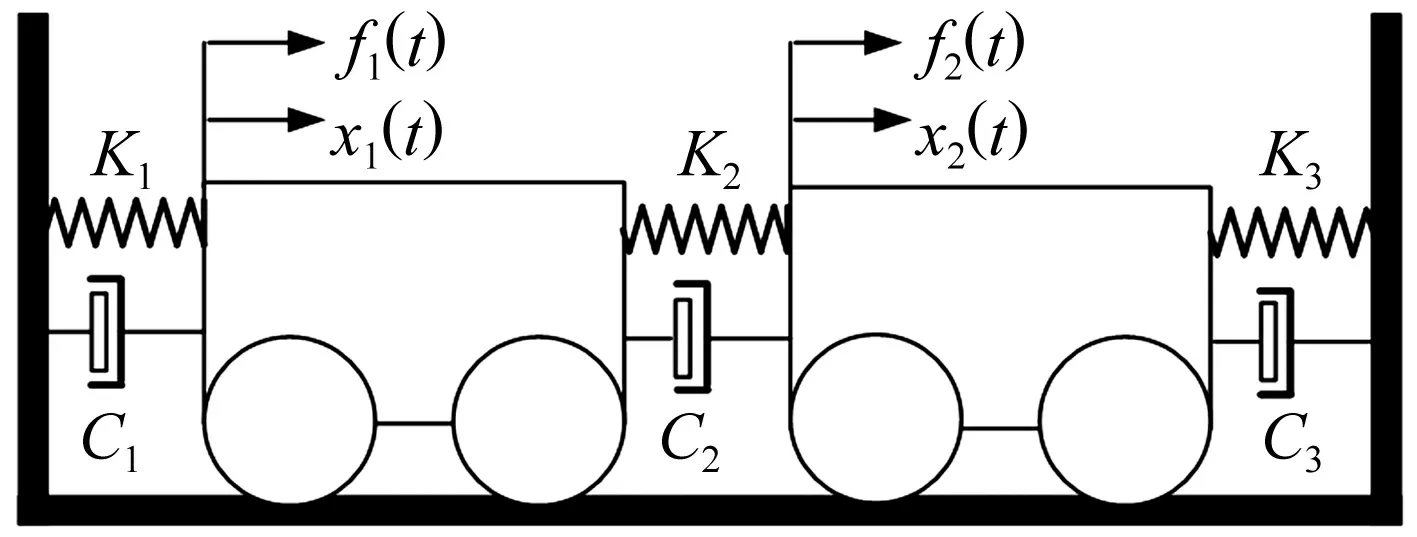
图1 两自由度阻尼振动系统

对上面两自由度阻尼振动系统，令:

k1=k2=k3=k=2 000 N/m

C1=C2=C3=c=3 N/(m·s-1)

M1=M2=m=2 kg

(31)

解得系统的无阻尼正则振型矩阵为:

(32)

由于模态阻尼阵:

(33)

为对角阵，所以该系统为经典阻尼系统。由振型迭加法可推得响应的解析表达式为:

(34)

其中:

由本文提出的方法，

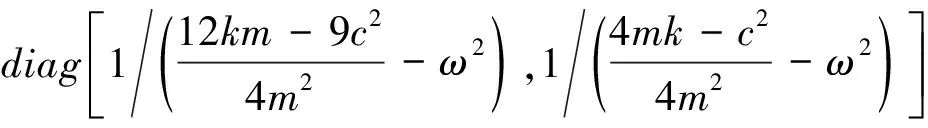
(35)

根据式(25)得:

(36)

表1 本文算法与振型迭加法计算响应解的比较

下面在时间6 s内，分别以时间步长Δt=0.25 s和Δt=1 s应用本文方法求解响应，并与振型迭加法的计算结果进行了比较，具体结果见表1。

从表1的结果看，对于经典阻尼系统的响应问题，本文方法的计算结果与振型迭加法的计算结果基本一致，而本文的响应表达式是通过解析方法得到的，这说明本文方法与振型迭加法的表达式是等价的。二者的偏差存在于振型迭加法需反复计算两倍于系统自由度数的反正切和三角正弦值，在计算机运算过程中不可避免地产生了误差的累积。

作为算例2，考虑如下的弹簧质量系统，如图2所示。

图2 弹簧质量系统

Fig.2 Spring-mass system

图中k1=0.95，k2=k3=…=k10=0.03，k11=1.05，m1=m2=…=m10=1.0，每个频率的自然阻尼系数都为0.05。用有限元方法提取系统的性质矩阵后，计算其无阻尼正则振型矩阵为:

由式(3)计算模态阻尼阵为:

表2 本文算法及Newmark法计算响应解的比较

D并非纯对角矩阵，因此该系统为非经典阻尼系统。设简谐激励为:

{f}=(F1,F2,F3,F4,F5,F6,F7,F8,F9,F10)Tsinωt

(37)

其中:F1=F3=F5=F7=F9=1,F2=F4=F6=F8=F10=2,ω=2。下面在时间2 s内应用本文方法求解响应，并与Newmark方法进行比较，结果见表2。

从表2的结果看，对于非经典阻尼系统的响应问题，本文方法与Newmark方法求得的响应值相近，即验证了本文方法的正确及可行性。二者的偏差存在于本文方法为解析解，而Newmark方法为数值解。而在计算效率方面，Newmark方法在每个时间步长上都需要求解一个未知数个数与自由度数相同的方程组，为了提高精度还需要缩小时间步长，势必带来计算量的增长，因此本文方法在计算效率及精度方面均优于Newmark方法。

6 结 论

本文提出了一种计算经典及非经典阻尼系统响应的新方法。只需利用任意动力系统所对应的无阻尼正则振型、无阻尼固有频率及模态阻尼阵，即可求得任意激励下经典及非经典阻尼动力系统的精确响应。本文提出的算法公式简洁、紧凑和精确，不存在计算误差，不仅在计算响应时使效率及精度均得到提高，而且还可作为优化目标函数应用于模型修正、结构设计优化及损伤识别等工程领域，有着良好的前景。

参 考 文 献

[1]徐医培，李素有，吴立言.结构动态响应的求解方法分析[J].机械设计与制造，2009,6:12-14.

XU Yi-pei,LI Su-you,WU Li-yan.Analysis about several methods of solving dynamic response of structures[J].Machinery Design & Manufacture,2009,6: 12-14.

[2]张森文，曹开彬.计算结构动力响应的状态方程直接积分法[J].计算力学学报，2000,17(1): 94-97.

ZHANG Sen-wen,CAO Kai-bin.Direct integration of state equation method for dynamic response of structure [J].Chinese Journal of Computation Mechanics,2000,17(1): 94-97.

[3]刘寒冰，张 淼，魏 健.结构动力响应分析的多重网格方法[J].吉林大学学报：工学版，2008，38(3)：619-623.

LIU Han-bing,ZHANG Miao,WEI Jian.Multigrid method for structure dynamic response analysis [J].Journal of Jilin University: Engineering and Technology Edition,2008,38(3): 619-623.

[4]蒲军平，刘 岩，王元丰，等.基于精细时程积分的结构动力响应降维分析[J].清华大学学报：自然科学版，2002，42(12)：1681-1683.

PU Jun-ping,LIU Yan,WANG Yuan-feng,et al.Structure dynamic response analysis by reduced dimensions based on a precise time-integration method [J].Journal of Tsinghua University: Science and Technology,2002,42(12): 1681-1683.

[5]郭兴旺，邹家祥.对机械振动系统的六种动态响应分析方法的评述[J].振动与冲击，1996,15(2): 43-46.

GUO Xing-wang,ZOU Jia-xiang.A review of six dynamic response analysis methods of mechanical vibration systems [J].Journal of Vibration and Shock,1996,15(2): 43-46.

[6]周锡元，马东辉，俞瑞芳.工程结构中的阻尼与复振型地震响应的完全平方组合[J].土木工程学报，2005,38(1): 31-39.

ZHOU Xi-yuan,MA Dong-hui,YU Rui-fang.Damping in structures and complete qudratic combination (CCQC)of complex mode seismic responses[J].China Civil Engineering Journal,2005,38(1): 31-39.

[7]Greco A，Santini A.Comparative study on dynamic analysis of non-classically dymped linear system[J].Structural Engineering and Mechanics,2002,14(6):679-698.

[8]Liu Z S，Song D T，Huang C.Vibration analysis of non-classically damped linear systems [J].Journal of Vibration and Acoustics,2004,126:456-458.

[9]徐 涛，程 飞，于 澜,等.非经典阻尼系统的求解[J].吉林大学学报：工学版，2006，36：49-52.

XU Tao,CHENG Fei,YU Lan,et al.Solution of non-classical damped system [J].Journal of Jilin University: Engineering and Technology Edition,2006,36: 49-52.

[10]Li W M，Hong J Z.Research on the iterative method for model updating based on the frequency response function [J].Acta Mechanica Sinica,2012,28(2):450-457.

[11]杨彦芳，宋玉普，纪卫红.基于实测频响函数主成分的在役网架损伤识别方法[J].振动与冲击，2007,26(9): 128-132.

YANG Yan-fang,SONG Yu-pu,JI Wei-hong.An identification method of existing truss structural damage bases on principal component analysis measured frequency response functions[J].Journal of Vibration and Shock,2007,26(9): 128-132.

[12]杨海峰，吴子燕，吴 丹.基于加速度频率响应函数的结构损伤测量方法研究[J].振动与冲击，2007,26(2): 90-92.

YANG Hai-feng,WU Zi-yan,WU Dan.Structural damage detection method based on acceleration frequency response function [J].Journal of Vibration and Shock,2007,26(2): 90-92.

[13]Ward H，Stefan L，Paul S.Modal analysis theory and testing[M].Katholieke Universiteit Levven,Brussel,Belgium,1997.