低雷诺数下串联双圆柱涡激振动机理的数值研究

郭晓玲， 唐国强,2， 刘名名， 吕 林,3， 滕 斌

(1．大连理工大学 海岸和近海工程国家重点实验室，大连 116024；2．韩国海洋科学技术研究所，大田 305-343；3．大连理工大学 深海工程研究中心，大连 116024)

在海洋工程中，当水流经过海洋平台的桩柱、支撑结构、立管及海底管线等这些非流线型结构时，会在尾流区内产生交替的旋涡脱落，使作用在结构上的流体作用力表现出明显的周期性特征，进而诱发涡激振动(Vortex-Induced Vibration，VIV)。当涡旋的脱落频率与结构的固有频率相接近时，将发生“锁定”现象。此时，结构物会以较大的振幅振动，导致结构物的寿命急剧降低。在过去的几十年中，均匀流中单个圆柱的涡激振动问题得到广泛的关注[1-6]。人们通过对高雷诺数实验研究发现，在低质量-阻尼比(m*ξ)下，圆柱的位移响应可以分为三个阶段[1]：初始分支(Initial branch)、上分支(Upper branch)及下分支(Lower branch)，而在高质量-阻尼比(m*ξ)情况下，圆柱的位移响应只存在初始分支和下分支[2]。通过强迫振动的实验研究发现[3]：对于仅发生横流向受迫振动的圆柱结构，其尾涡脱落模式通常可划分为2P、2S和P+S三种形式，从Khalak等[1]中可以看到，位移响应的初始分支对应的涡脱落模式为2S，下分支对应的为2P模式。

对于海洋工程结构中近距离放置的多个圆柱的情况，由于圆柱之间存在明显的水动力干涉作用，相应的涡激振动响应与单个圆柱的情况存在显著的差别[7-11]。针对上游圆柱固定不动，下游圆柱发生涡激振动的实验研究表明[7]，由于受到上游圆柱尾迹区的影响，下游圆柱开始发生锁定时所对应的约化速度大于单个圆柱的情况。并且，下游圆柱的锁定带宽与两圆柱的间距有关。例如，Brika等[7]的结果表明，当两圆柱间的相对圆心距L/D=10.0时，以约化速度表征的下游圆柱的锁定区间约为单圆柱情况的2倍。Carmo等[8]分别计算了二维(Re = 150)和三维(Re = 300)条件下，弹性支撑圆柱在上游固定圆柱尾流干涉作用下的横流向单自由度振动问题。计算条件为圆心间距分别为LX/D=1.5、3.0、5.0和8.0，质量比为m*=2.0，阻尼比为ξ=0.007。数值结果表明，在Re=150条件下，当发生共振时，下游圆柱的振幅较单圆柱情况增大近50%，而对于三维情况，在不同的圆心间距下，下游圆柱的振动幅值随约化速度的变化趋势与对应的二维情况类似。在以往的研究工作中，考虑到圆柱发生涡激振动时顺流向位移的振幅比较小，因此，顺流向的振动往往被忽略[8-9]。而Vandiver等[10]的研究工作表明，顺流向和横流向存在明显的相互作用。陈文曲等[11]也对这一方面开展了数值分析工作。但是，人们对低雷诺数流动中，处于固定圆柱尾迹干涉作用下，同时具有顺流向和横流向双自由度的圆柱涡激振动问题仍缺乏深刻的认识，特别是圆柱间距及质量比对圆柱受力和涡激振动响应的影响还需要更加细致的研究。

以目前现有的计算能力，对大尺度(几千米水深)范围内的实际立管涡激振动开展全场三维数值分析还面临很大的挑战，计算时间过长，不能满足实际工程设计的需要。但有关低雷诺数下，多圆柱涡激振动问题的数值研究对于发展可靠的数值模型以及建立快捷的近似工程分析预报方法是有借鉴意义的。因此本文的工作主要在于加深对多圆柱涡激振动现象物理本质的认识，更侧重于基础理论方面的研究。本文采用三步有限元数值方法对二维Navier-Stokes方程进行了求解，并结合任意拉格朗日-欧拉(ALE)动网格方法，建立和开发了相应的数值模型和计算程序，以Re=150为代表，重点研究了两个等直径串联圆柱的涡激振动问题，其中上游圆柱固定不动，下游圆柱在弹性支撑和阻尼作用下允许同时发生顺流向和横流向振动。通过数值计算，来研究圆柱间隙比、质量比以及约化速度等因素对下游圆柱涡激振动特性的影响。

1 数值模型

1.1 流动控制方程

二维不可压缩均匀粘性牛顿流体运动的基本控制方程为连续性方程和Navier-Stokes方程，在ALE参考坐标系下，可以表示成如下的无量纲形式：

(1)

(2)

其中，xi表示笛卡尔坐标(二维情况下i= 1、2，分别对应x和y方向)，ui为xi方向的流速分量，p为压力，Re=UD/υ为雷诺数，U为均匀来流流速，D为圆柱直径，υ为流体的运动学粘性系数,cj为对流速度，并有:

(3)

应用三步有限元方法[12-13]，可得到如下离散形式的动量方程：

(4)

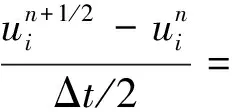
(5)

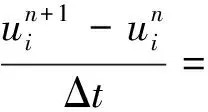
(6)

(7)

对于时间推进，本文根据CFL(Courant-Friedrichs-Lewy)条件，采用如下的动态时间步长：

式中，Se为网格的面积，ue为网格中心点的流速，min(*)表示在计算域内取最小值，Cs为安全系数，文中取为Cs= 0.2。

由于上述离散格式具有高阶Tayler-Galerkin性质，同时速度与压力通过投影(Projection)过程进行了解耦，因此式(4)～式(6)以及式(7)均可采用统一的标准Galerkin有限元方法进行空间离散，相关的离散方法可参见文献[12～14]。

当获得流场和压力场后，圆柱所受到的流体作用力可通过对圆柱表面的压力及粘性剪切力进行表面积分求得，无量纲化的拖曳力系数CD和升力系数CL分别为：

(8)

(9)

式中，p,u,v分别为圆柱表面上某点的压力、x方向速度、y方向速度，θ为该点与圆心的连线与x轴正向之间的夹角。

1.2 圆柱的运动方程

(10)

(11)

当圆柱的位移确定后，本文通过微分网格变换方法进行网格更新[15]，进而获得新的网格坐标以及网格运动速度，用于下一时间步的流场求解。

1.3 计算模型及边界条件

计算模型及边界条件如图1所示。两等直径圆柱串联放置，无量纲的圆柱直径为d=1。设坐标原点位于下游圆柱的初始圆心，两圆柱圆心间距为LX，相应的无量纲参数为LX/D。计算域的顺流向长度为55D，横流向宽度为50D。在入口处指定无量纲的速度u=1，v=0；侧壁采用了对称边界条件∂u/∂y=0，v= 0；出口处的速度边界条件为∂ui/∂t+c∂ui/∂xi=0，其中c为局部平均流速；圆柱表面施加不可滑移边界条件u=dx/dt，v=dy/dt。计算中，在出口处指定相对压力p= 0，在其他边界采用∂p/∂n=0的压力边界条件，n为指出流体域的外法向单位矢量。在初始时刻，流场中的速度及相对压力分布均设为零(即初始速度场满足连续方程)。

图1 计算域及边界条件示意图

2 模型验证

2.1 网格收敛性验证

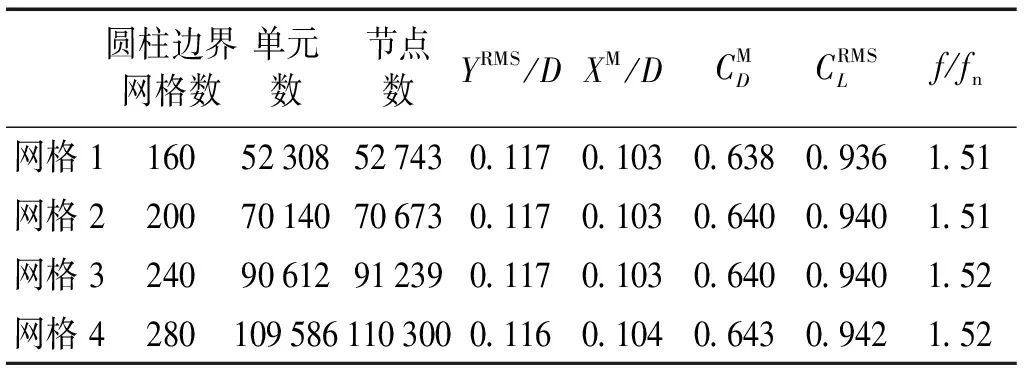
表1 网格收敛性验证结果

2.2 圆柱横流向涡激振动的数值验证

为进一步验证本文数值模型的可靠性，同时考虑到在之前的工作中已对固定单圆柱绕流问题进行了详细的验证[13]，以下仅对单个圆柱(Isolated)横流向自激振动以及上游圆柱固定，下游圆柱(直径同于上游圆柱)的横流向自激振动问题分别进行计算。在计算的过程中，均采用了相同的雷诺数Re=150、质量比m*=2.0和阻尼比ξ=0.007。图2给出了单圆柱横流向最大振幅(Amax/D)随约化速度(Ur)的变化及其与Carmo等[8]的对比结果。对于串联双圆柱的情况，考虑了LX/D= 1.5和3.0两种条件下，下游圆柱的横流向最大振幅对约化速度的依赖关系。从图2中可以看出，本文的数值计算结果(present)与已有数值结果吻合良好，表明本文的数值模型具有良好的数值精度。

3 计算结果及分析

在Carmo等[8]的数值分析工作中，考虑了上游圆柱固定不动的情况下，下游圆柱只在横流向发生涡激振动的问题。本文将对下游圆柱同时发生横流向和顺流向双自由度涡激振动的问题进行研究。为便于与文献[8]的结果进行对比分析，本文选择与该文相同的雷诺数Re=150、阻尼比ξ=0.007以及圆心间距比LX/D=3.0、5.0和8.0，在约化速度Ur= 3.0 ～ 12.0的范围内对下游圆柱的两自由度涡激振动响应特性开展研究。同时，本文进一步以m*= 5.0、10.0、20.0为例，研究质量比对下游圆柱发生涡激振动时动力响应的影响。

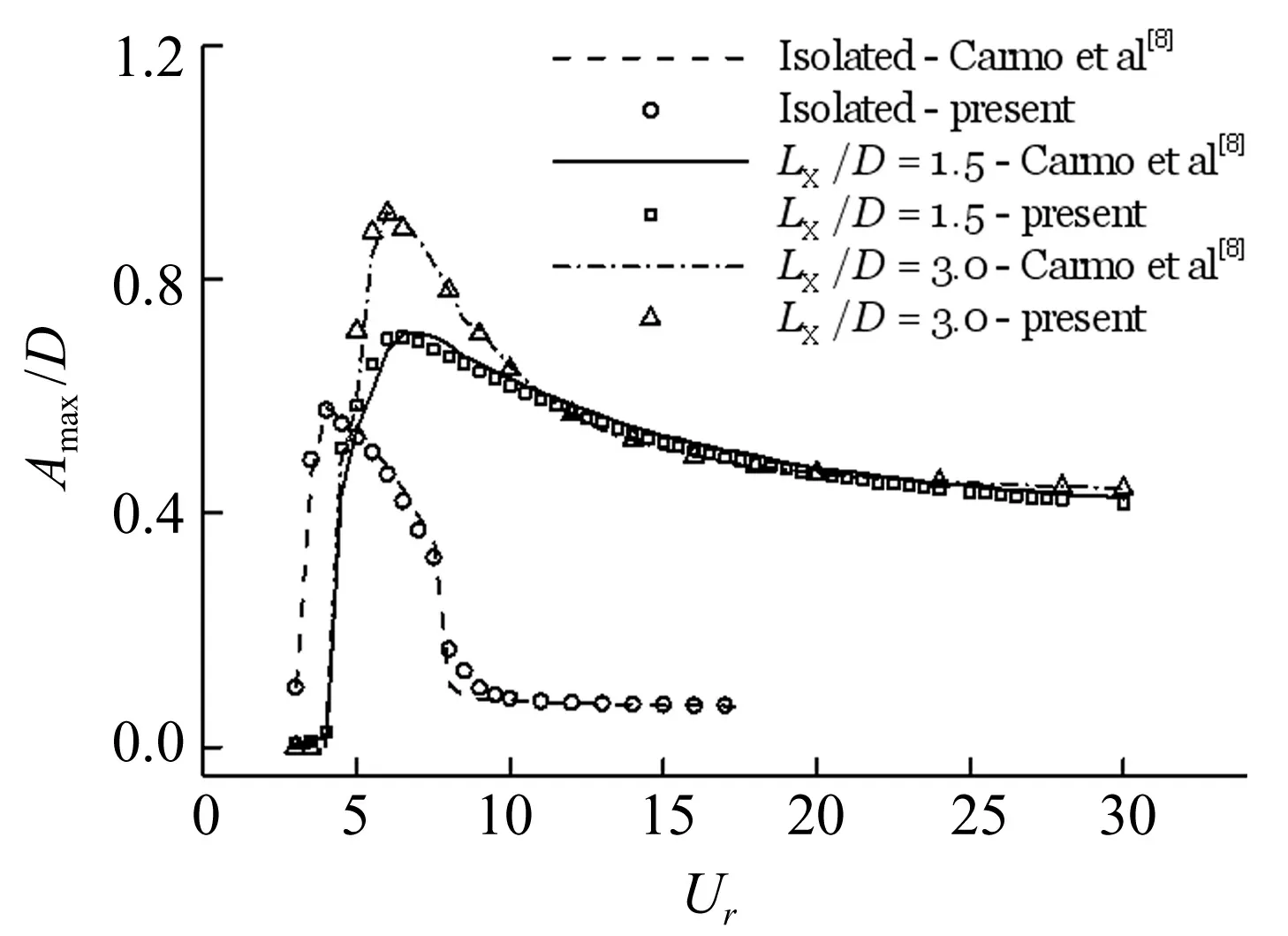
图2 单圆柱及下游圆柱横流向最大振幅Amax /D随约化速度Ur的变化(与文献[8]的对比，Re=150，m* = 2.0，ξ = 0.007)

3.1 圆心间距比的影响

根据固定串联圆柱的不同涡脱落模态[16-17]，本文选择了三个代表性的圆心间距比，LX/D= 3.0、5.0和8.0，并与相同雷诺数Re=150下的单圆柱(Isolated)涡激振动情况进行了比较，分析了圆柱的位移响应、振动频率、受力特性、尾涡脱落模式及运动轨迹的情况。

3.1.1 下游圆柱的位移及振动频率

图3(a)以质量比m*=10.0、阻尼比ξ=0.007为例，给出不同圆心间距下，下游圆柱横流向位移均方根YRMS/D随Ur的变化。从图中可以看出，当Lx/D=3.0时，其横流向位移响应曲线同单圆柱类似，只有一个峰，而Lx/D=5.0和8.0的YRMS/D曲线均出现了两个峰值。在Lx/D=3.0时，下游圆柱的最大位移均方根比单圆柱的情况增大近50%，而对于Lx/D=5.0和8.0，最大位移均方根约等于单圆柱的位移。从图3(a)中还可以看出，在Ur> 7.0的高约化速度范围内，与单圆柱的位移响应相比，下游圆柱的横流向位移依然维持在比较高的水平，并且Lx/D=5.0和8.0的位移均方根在幅值和变化趋势上都很接近，二者均比Lx/D=3.0所对应的位移明显偏大。

图3 不同圆心间距比LX / D下，下游圆柱涡激振动响应特性随约化速度Ur的变化关系(Re = 150，m* = 10.0，ξ = 0.007)

由图3(b)中下游圆柱的顺流向平均位移XM/D随约化速度Ur的变化曲线可以看到，随着Ur的增大，下游圆柱的顺流向平均位移也逐渐增大。同时，由于受到上游固定圆柱遮蔽效应的影响，下游圆柱的顺流向平均位移在各圆心间距下都小于单圆柱的情况。对于Lx/D=3.0的情况，在Ur≤5.5时，下游圆柱的XM/D出现负值，即下游圆柱向上游偏移，当发生锁定时，XM/D明显增大，在Ur>7.0后，XM/D基本随Ur呈线性增加。对于Lx/D=5.0和8.0的情况，顺流向平均位移与横流向位移均方根的变化趋势类似，在发生锁定前各出现一个次峰，锁定后，二者接近重合，并且随着Ur的增大基本呈线性增加，在量值上与Lx/D=3.0的情况接近。

图4给出了不同圆心间距比下，下游圆柱相对振动频率f/fn随Ur的变化关系及其与单圆柱情况的比较。对于圆柱结构的涡激振动问题，当圆柱的振动频率与固有频率接近时(即f/fn趋近于1.0，以下以0.95≤f/fn≤1.05为界)，一般可认为发生锁定[18]。图4表明，单圆柱的锁定区间约为5.0 ≤Ur≤6.5，而对于串联双圆柱的情况，在Lx/D=3.0时，下游圆柱的锁定区间为6.0≤Ur≤7.0，当Lx/D=5.0和8.0时，在本文考虑的约化速度范围内，锁定区间分别为 6.0≤Ur≤12.0和6.5≤Ur≤12.0。图4关于锁定区间的结果与图3 (a)的位移响应呈现出良好的对应关系，即圆柱振动的锁定区间对应着横流向位移比较大的区间。从图4中同时也可以发现，随着Lx/D的增大，开始发生锁定的临界约化速度也呈现出增大的趋势，并且对于Lx/D=5.0和8.0的情况，锁定区间明显大于单圆柱及Lx/D=3.0的情况。值得注意的是，在Lx/D=5.0和8.0时，横流向位移的第一个峰值出现在锁定发生之前。

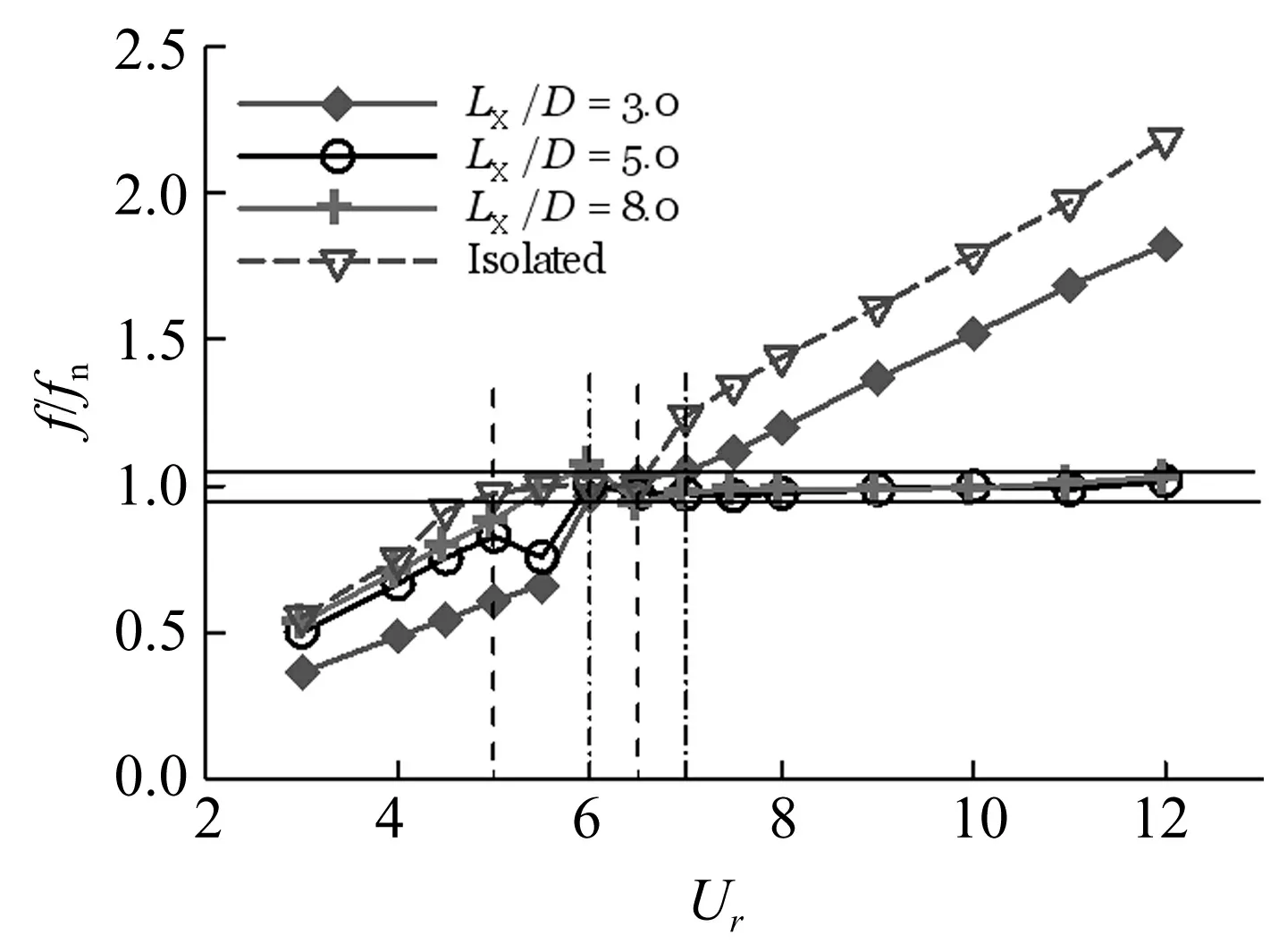
图4 不同圆心间距比LX / D下，下游圆柱横流向相对振动频率f/fn随约化速度Ur的变化关系(Re = 150，m* = 10.0，ξ = 0.007)

3.1.2 下游圆柱的受力特性

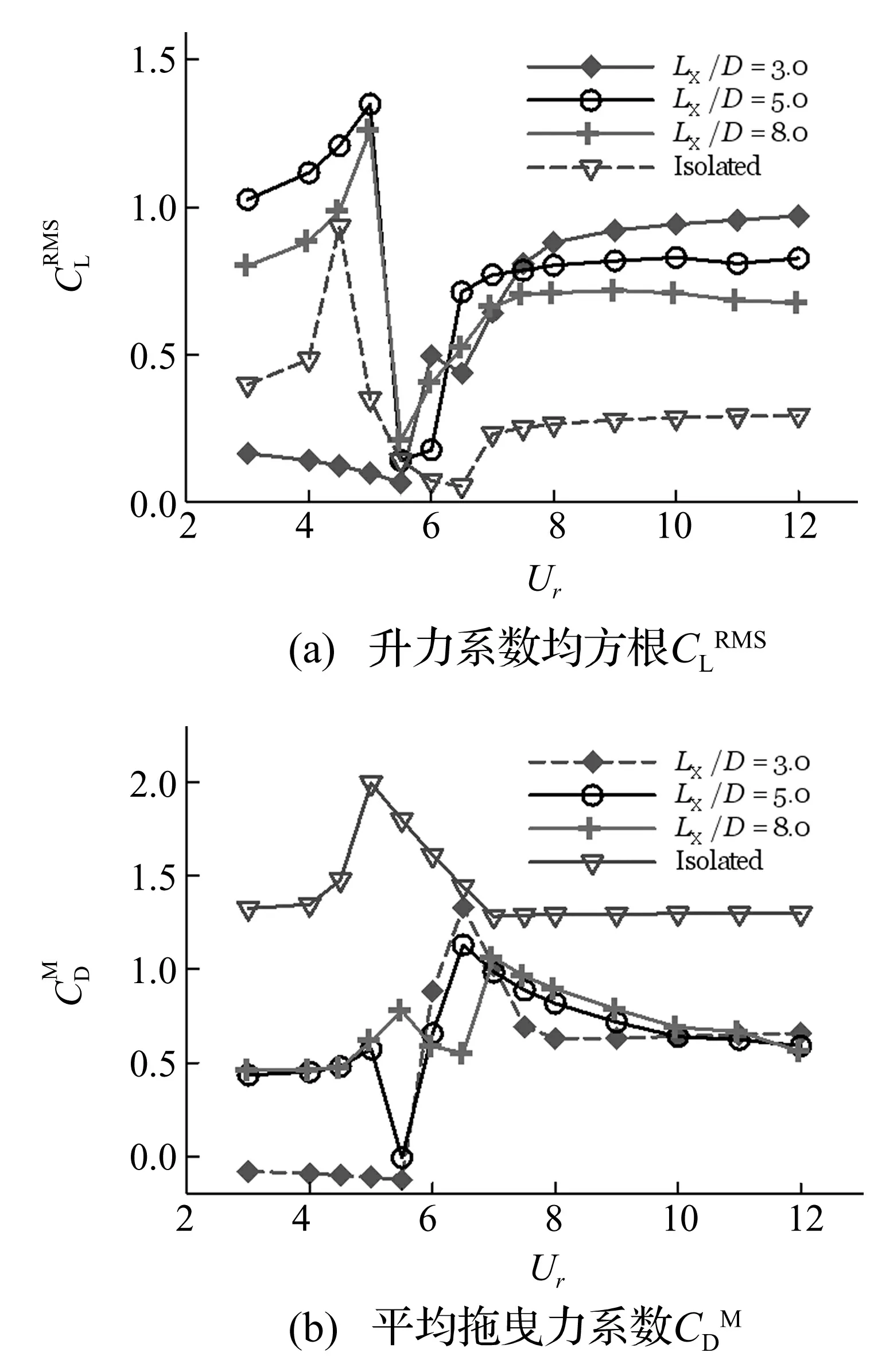
图5 不同圆心间距比LX / D下，下游圆柱受力特性随约化速度Ur的变化关系(Re=150，m*=10.0，ξ= 0.007)

3.1.3 尾涡脱落模式

图6分析了Lx/D及Ur对尾涡脱落模式的影响作用。对于Lx/D=3.0的串联双圆柱，数值结果表明，在Ur<6.0的范围内，上游固定圆柱后方没有涡旋脱落，圆柱系统尾流区内的旋涡以图6(a1)和6(a2)的模式进行整体脱落；当Ur≥6.0，即开始发生锁定后，上游圆柱后方开始出现涡脱落，如图6(a3)所示；随着Ur的进一步增大，下游圆柱不再发生锁定时，其尾涡脱落模式(参见图6(a4))相对锁定区内的图6(a3)未见明显变化。当Lx/D=5.0时，在Ur<5.5的范围内，典型尾涡脱落模式如图6(b1)所示，上游固定圆柱后方发生交替的涡旋脱落，而下游圆柱的尾涡则整齐地排成两排；当Ur=5.5时，尾涡模式如图6(b2)所示，整体上与图6(a1)及6(a2)的情况类似；当Ur≥6.0后，尾涡模式如图6(b3)和6(b4)所示，上、下游圆柱尾流区内分别可见旋涡的脱落。从前文的图3和图5中看到，在Lx/D=5.0，Ur=5.5的条件下，其位移和受力会突然变小，这正是由于当Ur=5.5时，尾涡脱落模式的突然改变所致。对于Lx/D=8.0，由于圆柱间距比较大，随着Ur的变化，上下游圆柱的尾流区内始终同时存在旋涡的脱落，参见图6(c1)-(c4)，上游圆柱脱落的涡旋经充分发展后，与下游圆柱的尾涡发生更为明显的干涉作用。

3.1.4 下游圆柱的运动轨迹

为说明下游圆柱在x和y两个自由度方向运动的相互影响作用，图7给出了不同圆心间距比和约化速度下的运动轨迹。其中，图7(a1)、图7(a2)、图7(b1)和图7(c1)中右下角分别给出了放大后的轨迹曲线。从图7(a1)-(a4)中可以看到，在相同的圆心间距比Lx/D=3.0下，随着Ur的增大，下游圆柱的运动轨迹始终是“8”字形的封闭曲线。而对于Lx/D=5.0和8.0，当Ur≤5.0时，下游圆柱的运动轨迹类似于Lx/D=3.0的情况，也为“8”字形。当Ur>5.0后，圆柱的轨迹则变为不封闭的且不规则的曲线，如图7(b3)-(b4)及7(c3)-(c4)所示。这说明圆心间距比和约化速度对下游圆柱的运动有明显的影响。当Lx/D比较小时，下游圆柱在两自由度方向上运动的相关性并不随约化速度有明显的变化。而当Lx/D较大时，Ur> 5.0后，圆柱在x和y方向运动的相互影响作用则由简单变得复杂。

图6 不同圆心间距比Lx /D及约化速度Ur下的尾涡脱落模式(Re = 150，m*=10.0，ξ=0.007)

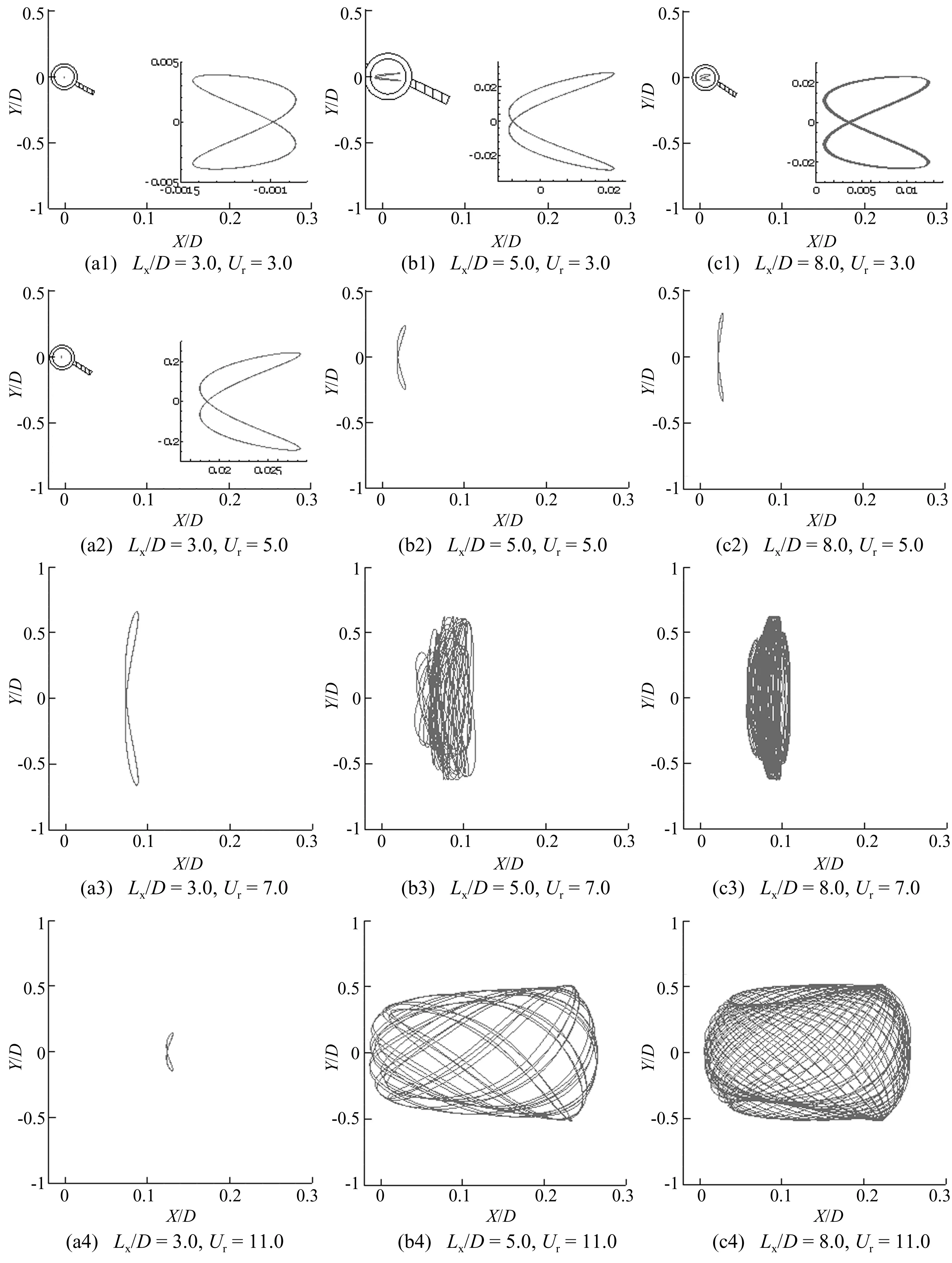
图7 不同圆心间距比Lx / D及约化速度Ur下下游圆柱的运动轨迹(Re=150，m* = 10.0，ξ = 0.007)

3.2 质量比对下游圆柱涡激振动的影响

质量比是圆柱结构涡激振动响应的重要影响因素之一，但对于多圆柱问题，相对于前述的间隙比和约化速度，人们对质量比的影响作用还缺乏细致的研究和足够的了解。在此，本文将以Lx/D=5.0为例，考虑三种不同的质量比m*= 5.0、10.0和20.0，对这一问题开展进一步的数值计算，分析质量比对圆柱的位移响应、振动频率、锁定区间、受力特性、尾涡脱落模式及运动轨迹的影响。

3.2.1 下游圆柱的位移及振动频率

图8首先给出了下游圆柱横流向相对振动频率f/fn随约化速度Ur的变化情况。从图中可以看出，在本文所考虑的参数范围内，质量比对锁定区间的影响作用不大，三种质量比下，锁定区间所对应的约化速度范围均为6.0≤Ur≤12.0。

图9给出了不同质量比下，下游圆柱的振动响应随约化速度的变化情况。图9(a)的结果表明，在锁定区间内，下游圆柱的横流向位移均方根总体上随约化速度的增大而逐渐减小。同时，在相同Ur下，m*越小，YRMS/D越大。而在未发生锁定的低约化速度范围内，在m*=20.0的条件下，YRMS/D随着Ur的增大持续增大，直到发生锁定时达到极值；对于相对较小的质量比m*=5.0和10.0，二者的YRMS/D在发生锁定前均出现跳跃。进一步的流场分析结果表明，m*=5.0，Ur=4.5和m*=10.0，Ur=5.5两个跳跃点均由尾涡脱落模式的改变所致，这说明质量比的变化也会对涡激振动过程中的流动模式和位移响应产生影响作用。

图9(b)考察了下游圆柱顺流向平均位移XM/D随Ur的变化情况。从图中可以看出，顺流向平均位移总体上均随着Ur的增大呈上升趋势，质量比越大，圆柱向下游偏移的平均位移越小。对于m*=5.0和10.0，XM/D也分别在Ur=4.5和5.5处发生跳跃，这与图9(a)的情况类似。

值得说明的是，在m*=5.0和20.0的情况下，相对于m*=10.0，下游圆柱在x,y两个方向的联合位移形态没有本质性的改变，与图7(b1)-(b4)所给出的运动形式在总体上基本一致。这表明，在本文所考查的参数范围内，质量比对下游圆柱纵向-横向运动的相干性的影响作用有限。

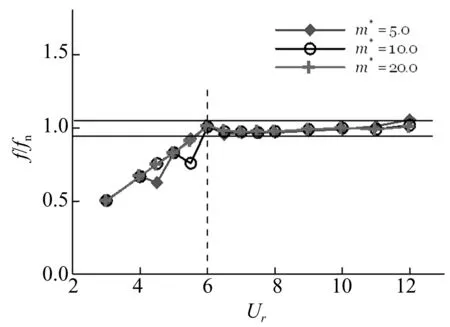
图8 不同质量比m*下，下游圆柱横流向相对振动频率f / fn随约化速度Ur的变化关系(Re = 150，Lx / D = 5.0，ξ = 0.007)

图9 不同质量比m*下，下游圆柱涡激振动响应特性随约化速度Ur的变化关系(Re =150，Lx / D = 5.0，ξ = 0.007)

3.2.2 下游圆柱的受力特性

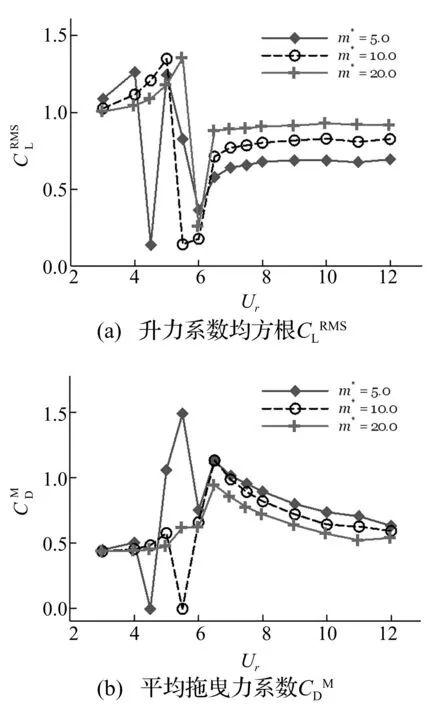
图10 不同质量比m*下，下游圆柱受力特性随约化速度Ur的变化关系(Re=150，Lx/D=5.0，ξ=0.007)

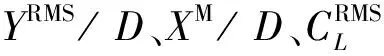
4 结 论

本文利用迎风有限元数值方法对不可压缩粘性流体的Navier-Stokes方程进行了求解，并结合ALE动网格方法，对Re=150条件下，串联双圆柱的涡激振动问题开展了二维数值分析。其中，上游圆柱固定不动，下游圆柱在弹簧和阻尼约束下允许同时发生顺流向和横流向的运动。在对数值模型的可靠性进行了验证的基础上，重点研究了两等直径圆柱圆心间距、质量比以及约化速度对下游圆柱涡激振动响应的影响作用，包括位移响应、振动频率特征、锁定区间、流体作用力、尾涡模式以及运动轨迹等方面。数值结果表明，在本文的计算范围内，随着两圆柱间相对圆心间距Lx/D的增大，下游圆柱开始发生锁定时对应的约化速度增大，在较大的间距比下(Lx/D=5.0和8.0)，锁定区间较单圆柱及小间距情况(Lx/D=3.0)明显变宽。在Lx/D=3.0的小间距下，下游圆柱的横流向振动位移可达到单圆柱情况下的1.5倍，同时下游圆柱的顺流平均位移出现负值，即下游圆柱的平衡位置向上游圆柱移动。数值结果也表明，随着约化速度和间距比的变化，串联圆柱的尾涡模式会发生显著改变，进而深刻影响圆柱的受力和运动响应。本文还以Lx/D= 5.0为典型间距，研究了质量比对下游圆柱涡激振动响应和受力特性的影响。结果表明，质量比对锁定区间的影响不明显，但当锁定发生时，在相同约化速度下，随着质量比的增大，下游圆柱的横流向运动位移响应会有所减小。进一步的流场分析表明，质量比的变化也会导致尾涡脱落模式的改变，进而影响到圆柱的受力和运动特性，这在进入锁定区间前非常明显。

目前关于两自由度涡激振动问题的研究，通常固定雷诺数，考虑运动响应等对约化速度的依赖关系。但对实际问题而言，往往是圆柱结构形式和流体物性一定，来流流速发生改变，此时雷诺数和约化速度同时发生变化。因此，固定雷诺数而仅改变约化速度的研究方法不能满足全面了解涡激振动特性的需要，这是在以后的研究工作中需要加以关注的问题。另一方面，随着雷诺数的不断增加，二维模型将不再适用，需要开展三维数值计算。本文的计算结果也表明，即便是在简单的二维低雷诺数条件下，约化速度的微小变化也会引起涡激振动响应特性的剧烈改变，这就要求采用很小的约化速度增量来开展细致的数值分析工作，这些都会导致计算量的激增，对现有的计算条件提出了较大的挑战。此外，在高雷诺数条件下，直接数值模拟(Direct Numerical Simulation)在理论上是可靠的，但计算量巨大。采用湍流模型虽可缓解计算量的压力，但湍流模式本身的适用性问题至今仍是全人类共同面对科学难题之一。

参 考 文 献

[1]Khalak A，Williamson C H K.Motions,forces and mode transitions in vortex-induced vibrations at low mass-damping [J].Journal of Fluids and Structures，1999，13(7-8)：813-851.

[2]Feng C C.The measurement of vortex induced effects in flow past stationary and oscillating circular and D-section cylinders [D].Vancouver：University of British Columbia，1968.

[3]Williamson C H K，Roshko A.Vortex formation in the wake of an oscillating cylinder [J].Journal of Fluids and Structures，1988，2(4)：355-381.

[4]何长江，段忠东.二维圆柱涡激振动的数值模拟 [J].海洋工程，2008，26(1)：57-63.

HE Chang-jiang，DUAN Zhong-dong.Numerical simulation of vortex-induced vibration on 2D circular cylinders [J].The Ocean Engineering，2008，26(1)：57-63.

[5]方平治，顾 明.圆柱两自由度涡激振动的数值模拟研究 [J].同济大学学报(自然科学版)，2008，36(3)：295-298.

FANG Ping-zhi，GU Ming.Numerical simulation for vortex-induced vibration of circular cylinder with two degree of freedoms [J].Journal of Tongji University (Nature Science)，2008，36(3)：295-298.

[6]唐国强.立管涡激振动数值模拟方法及物理模型实验 [D].大连：大连理工大学，2011.

[7]Brika D，Laneville A.The flow interaction between a stationary cylinder and a downstream flexible cylinder [J].Journal of Fluids and Structures，1999，13(5)：579-606.

[8]Carmo B S，Sherwin S J，Bearman P W，et al.Flow-induced vibration of a circular cylinder subjected to wake interference at low Reynolds number [J].Journal of Fluids and Structures，2011，27(4)：503-522.

[9]Bao Y，Zhou D，Tu J H.Flow interference between a stationary cylinder and an elastically mounted cylinder arranged in proximity [J].Journal of Fluids and Structures.2011，27(8)：1425-1446.

[10]Vandiver J K，Jong J Y.The relationship between in-line and cross-flow vortex-induced vibration of cylinders [J].Journal of Fluids and structures，1987，1(4)：381-399.

[11]陈文曲，任安禄，李广望.串联双圆柱绕流下游圆柱两自由度涡致振动研究 [J].力学学报，2004，36(6)：732-738.

CHEN Wen-qu，REN An-lu，LI Guang-wang.The Numerical study of two-degree-of -freedom vortex-induced vibration of the downstream cylinder in tandem arrangement [J].Chinese Journal of Theoretical and Applied Mechanics，2004，36(6)：732-738.

[12]Jiang C B，Kawahara M.The analysis of unsteady incompressible flows by a three-step finite element method [J].International Journal for Numerical Methods in Fluids，1993，16(9)：793-811.

[13]Lu L，Qin J M，Teng B，et al.Numerical investigations of life suppression by feedback rotary oscillation of circular cylinder at low Reynolds number [J].Physics of Fluids，2011，23(3)：033601.

[14]Lu L，Cheng L， Teng B，et al.Numerical investigation of fluid resonance in two narrow gaps of three identical rectangular structures [J].Applied Ocean Research，2010，32(2)：177-190.

[15]吕 林.海洋工程中小尺度物体的相关水动力数值计算 [D].大连：大连理工大学，2006.

[16]Zdravkovich M M.The effects of interference between circular cylinders in cross flow [J].Journal of Fluids and Structures，1987，1(2)：239-261.

[17]Carmo B S，Meneghini J R，Sherwin S J.Secondary instabilities in the flow around two circular cylinders in tandem [J].Journal of Fluid Mechanics，2010，644：395-431.

[18]Leontini J S，Stewart B E，Thompson M C，et al.Predicting vortex-induced vibration from driven oscillation results [J].Applied Mathematical Modelling，2006，30(10)：1096-1102.