超高层钢-混凝土混合结构地震损伤模型研究

蒋欢军,朱剑眉,陈 前

(1.同济大学 结构工程与防灾研究所，上海 200092；2.同济大学 建筑设计研究院，上海 200092)

由于城市发展的需要和建筑技术进步的推动，世界各地超高层建筑数量逐渐增多。为了适应建筑高度的不断突破，新的结构体系应运而生，而钢-混凝土混合结构体系由于其具有的独特优势，在我国目前已建成的超高层建筑中得到了广泛的应用。目前钢-混凝土混合结构体系的理论研究一定程度上落后于工程实践，其在地震作用下的损伤发展及演化过程不甚明确[1]，加之我国是遭受地震灾害最为严重的国家之一，因此深入研究钢-混凝土混合结构在地震作用下的损伤过程、损伤机理与损伤评估方法具有深远的现实意义。

从结构地震倒塌反应的全过程来看，结构的破坏是损伤不断累积发展的过程[1]，因此从损伤评估的角度研究结构的破坏是一种较为合理的途径。

国内外大量震害实例及相关实验研究表明，结构的地震破坏形式可归结为结构中的最大反应(强度、位移、延性等)首次被超越和累积损伤破坏两种类型，从而形成了首次超越破坏准则(强度准则、变形准则、能量准则)及能量和变形双控准则[2]。强度准则是最早的破坏准则，该准则能较好地反映结构从弹性到塑性的过程，但随着对地震非线性问题研究的深入，用强度准则描述结构屈服后的变形能力存在一定的局限性。为准确描述结构进入弹塑性过程后的破坏情况，学者们又提出了变形破坏准则。随后，为弥补变形破坏准则不能反映持时对结构累积破坏的影响，Houser[3]首先提出了用结构累积变形能来衡量结构在地震下是否发生破坏，即为能量准则，但由于难以确定采用何种形式的能量作为破坏指标而未得到广泛应用。双重累积破坏准则同时考虑结构的最大反应和累积损伤的影响，能很好地解释地震动三要素(振幅、频谱、持时)各自对结构破坏的影响，目前已得到了大家的公认，其中最大变形与累积耗能的组合是应用最为广泛的。

目前，结构损伤理论的研究主要集中在材料、构件及结构三个层次。构件层次的损伤模型主要指直接从结构构件出发，建立能够描述结构构件损伤过程的损伤模型。陈鑫等[4]对Park-Ang模型进行修正，考虑轴压比系数和体积配箍率等因素，来反映高强混凝土柱的损伤发展过程。侯圣吉[5]分析了剪跨比、混凝土强度和轴压比对型钢高强高性能混凝土框架柱抗震性能的影响，提出了基于变形和累积耗能非线性组合的型钢高强高性能混凝土框架柱地震损伤模型。

在结构层次的损伤研究理论分析方面，主要有加权法和整体法。目前被普遍接受的对整体结构的损伤评估方法是加权法，它将结构尺度损伤视为构件尺度损伤的函数，即借助权重系数将构件层次上的损伤加权组合，获得整体结构的损伤信息。Park等[6]将各构件的耗能比作为权重系数，由构件损伤加权得到楼层损伤，再由楼层损伤得到整体结构的损伤。牛狄涛等[7]认为结构薄弱层和发生损伤的楼层位置对整体结构损伤有着重要影响，直接采用构件损伤指数比来加权得到整体结构损伤。刘良林等[8]基于等效线性方法，在Ghobarah整体损伤评价模型的基础上提出了新的结构整体损伤指数计算式。罗欣等[9]采用能量耗散系数和最大变位处的卸载刚度的退化为破坏参数，提出了适用于高强混凝土剪力墙构件的双参数地震损伤模型。

总体而言，目前针对钢筋混凝土结构的损伤研究较多，而针对钢-混凝土混合结构的整体损伤模型的研究尚待深入，且未提出考虑不同类型构件重要性区别的损伤模型。对于钢-混凝土超高层结构，其构件类型较多，不同类型构件的地震损伤对于结构整体安全性的影响大小不同，所建立的损伤模型亦需考虑这一点。

本文基于已有的研究成果，提出了考虑不同构件重要性、楼层位置以及损伤值大小，适用于典型超高层钢-混凝土混合结构(型刚混凝土框架-混凝土核心筒结构)损伤特点的整体结构地震损伤模型。

1 楼层地震损伤模型的建立

1.1 构件地震损伤模型

本文认为仅仅从最大变形或累积耗能单方面来考虑构件的损伤，难以真实反映构件的破坏机理，因为构件的最大变形和累积损伤是相互影响的，随着累积损伤的增加，最大变形的位移界限不断降低；相应地，随着最大变形的增加，累积损伤的控制界限也在下降。合理的地震损伤模型应该包含最大变形和滞回耗能两个指标。因此，本文采用基于最大变形和滞回耗能的双参数地震损伤模型来计算构件的损伤指标，选取适合于典型超高层钢-混凝土混合结构型钢混凝土框架-混凝土核心筒的各主要构件(型钢混凝土柱、钢梁、钢筋混凝土剪力墙和连梁)的地震损伤模型。

对于型钢混凝土柱，基于王东升等[10]提出的改进的Park-Ang双参数模型，刘阳等[11]通过对完成的型钢混凝土柱试验数据的拟合得出了考虑配钢率、剪跨比和配箍率的耗能因子β，该损伤模型表达如下：

(1)

β=-0.002ρa+0.005λ+0.01ρw

(2)

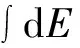
对于钢梁，本文利用Chai等[12]基于57个钢悬臂构件试验提出的修正的Park-Ang双参数损伤模型，该模型预测与试验结果吻合良好，较好地反映出了钢构件的损伤发展特点，模型表达形式如下：

(3)

式中:Ehm为单调加载下结构的塑性耗能，其他符号意义同式(1)，β*取为0.23。

对于钢筋混凝土剪力墙和连梁，采用本课题组提出的修正的Park-Ang地震损伤模型[13]，该模型较好地解决了Park-Ang损伤模型上下界不收敛的问题，可以更真实地反映钢筋混凝土构件的地震损伤性能，具体表示形式如下：

(4)

(5)

对于某一类型构件，其损伤值越大对本类型构件的损伤值的影响越大。基于这种想法，本文将同一楼层的同类型所有构件按照损伤值权重系数加权求得各类型构件的损伤值，即：

(6)

(7)

1.2 楼层地震损伤模型的建立

目前，通过构件的损伤指标的加权组合得到楼层的损伤指标的关键在于如何确定各类构件的权重系数。合理的权重系数要能够反映构件在结构整体中的相对重要程度。

本文将结构中的构件分为关键构件、主要构件和次要构件。对于型钢混凝土框架-混凝土核心筒结构，剪力墙和框架柱为结构的关键构件，框架梁为主要构件，连梁是体系中最先破坏且损伤最严重的构件，连梁的破坏对结构整体损伤的影响不大，属于次要构件。

根据不同类型构件的重要性给出不同的加权系数来计算楼层的地震损伤指标，构件的破坏对楼层的失效及抗震性能影响越大，相应给出的加权系数越大，影响越小加权系数越小。本文提出的楼层地震损伤模型如下：

(8)

(9)

(10)

(11)

(12)

式中，a,b,c,d为四类基本构件的相对重要性系数。

图1 迭代法确定系数的a,b,c,d流程图

依据上述重要性分析，有a>b>c>d。利用MATLAB软件，根据图1所示的流程图，通过迭代的方法确定合适的构件相对重要性系数a,b,c,d。

通过对一个典型型钢混凝土框架-混凝土核心筒结构某楼层失效时该楼层的地震损伤指标为1的条件迭代计算得到四类构件的相对重要性系数分别为：a=3.5，b=2.8，c=2.3，d=1.6。

2 整体结构地震损伤模型的建立

采用加权组合法建立整体结构的地震损伤模型，其表达形式如下：

(13)

式中，λj为第j层的楼层加权系数，Dj表示第j层的楼层损伤值，N为结构的楼层总数。

现有的加权组合法在确定楼层的加权系数时一般只考虑单个因素的影响，考虑不够全面。本文考虑了楼层位置系数γj与楼层损伤值系数ωj二者组合的形式。

2.1 楼层位置系数的计算

对于一般结构来说，底部楼层的重要性远比上部楼层大，对于超高层混合结构而言，一般底部几层都属于需要加强的部位。本文对杜修力[14]提出的线性楼层位置相对重要性系数进行了指数修正，提出了非线性的楼层位置系数，表达式如下：

(14)

式中，γj为第j层的楼层位置系数，j表示楼层号，N表示楼层总数。

图2为以一幢36层建筑为例，采用上述表达式绘制的楼层位置系数随楼层变化的关系曲线，可以看出，对于楼层数较多的超高层建筑，该位置系数在下部楼层变化相对比较缓慢。

图2 楼层位置系数随楼层变化关系曲线

2.2 楼层损伤值系数的计算

一般来说，损伤值越大的楼层对结构整体损伤的贡献越大。因此本文假定损伤值最大的楼层损伤值权重系数为1，其他楼层按该层损伤值与最大楼层损伤值的相对大小关系作为权重系数。楼层损伤值系数的计算公式如下：

(15)

式中，ωj为第j层的楼层损伤值系数，Dj表示第j层的楼层损伤值，Dmax为各楼层的最大损伤值。

2.3 楼层损伤权重系数计算

为了同时考虑楼层位置系数与损伤值系数二者的影响，考虑下述组合形式，具体的表达式为：

(16)

式中，λj为第j层的楼层损伤权重系数，N表示楼层总数。

3 算例结构

一个典型的型钢混凝土框架-混凝土核心筒结构由型钢混凝土柱、钢框架和钢筋混凝土核心筒组成。结构总高度110.2 m，首层高4.0 m，2～3层高3.6 m，其余各层高均为3.0 m。地上总计36层，标准层的结构平面布置如图3所示。结构按8度(0.20 g)进行抗震设计，场地类别为Ⅱ类，设计地震分组为第一组，场地特征周期为0.35 s。

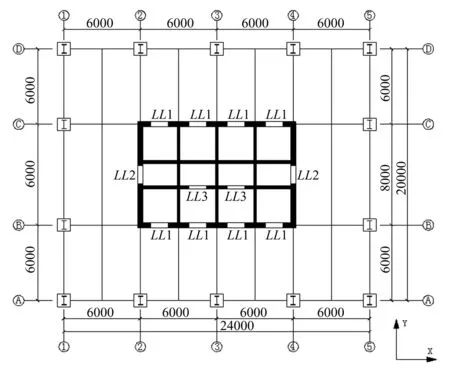
图3 结构标准层平面图

采用中国建筑科学研究院开发的PKPM和SATWE软件完成结构的截面设计和配筋计算，采用CSI公司开发的ETABS软件进行复核，采用Perform-3D软件建立结构的非线性数值计算模型，进行非线性地震反应和损伤计算分析。

根据设计反应谱选取了10条地震波进行时程分析，其中8条为天然波，2条为人工波，输入的地震波如表1所示，名称为User1和User2的地震波为单向的拟合设计反应谱的人工波。各条地震波的加速度反应谱与规范设计反应谱的比较如图4所示，图中粗实线为规范反应谱，粗虚线为所选地震波反应谱平均值曲线。从反应谱曲线可以看出，所选地震波的反应谱与规范反应谱基本在统计意义上相符。

图4 各条地震波的加速度反应谱曲线

分别输入X向为主和Y向为主的地震加速度记录进行时程计算，并逐渐加大峰值加速度，直到结构破坏为止。本文所建立的混合结构模型，竖向不存在刚度突变或结构不连续，也不存在薄弱层，此时，结构的破坏出现在结构的底层，即是由于底层的失效导致结构的失效。故本文以底层框架柱失效导致底层失效破坏作为结构失效的判别标准。

美国规范ATC-40将房屋遭受地震后，可能遭受的状态分为IO(Immediate Occupancy)、LS(Life Safety)、CP(Collapse Prevention)，可解释为“立即居住” 、“生命安全”和“防止倒塌”。

ATC- 40 给出了梁、柱、墙等构件在上述几种相应状态下的塑性限值，无论何种类型铰，都可以用图5表示，纵轴表示轴力、弯矩、剪力等,横轴表示轴向变形、曲率、转角等，其中B、IO、LS、CP、C为性能点,B点表示构件出现塑性铰，进入塑性状态，C点表示构件丧失承载能力，为失效点。各性能点所对应的横坐标为相应的弹塑性位移限值。

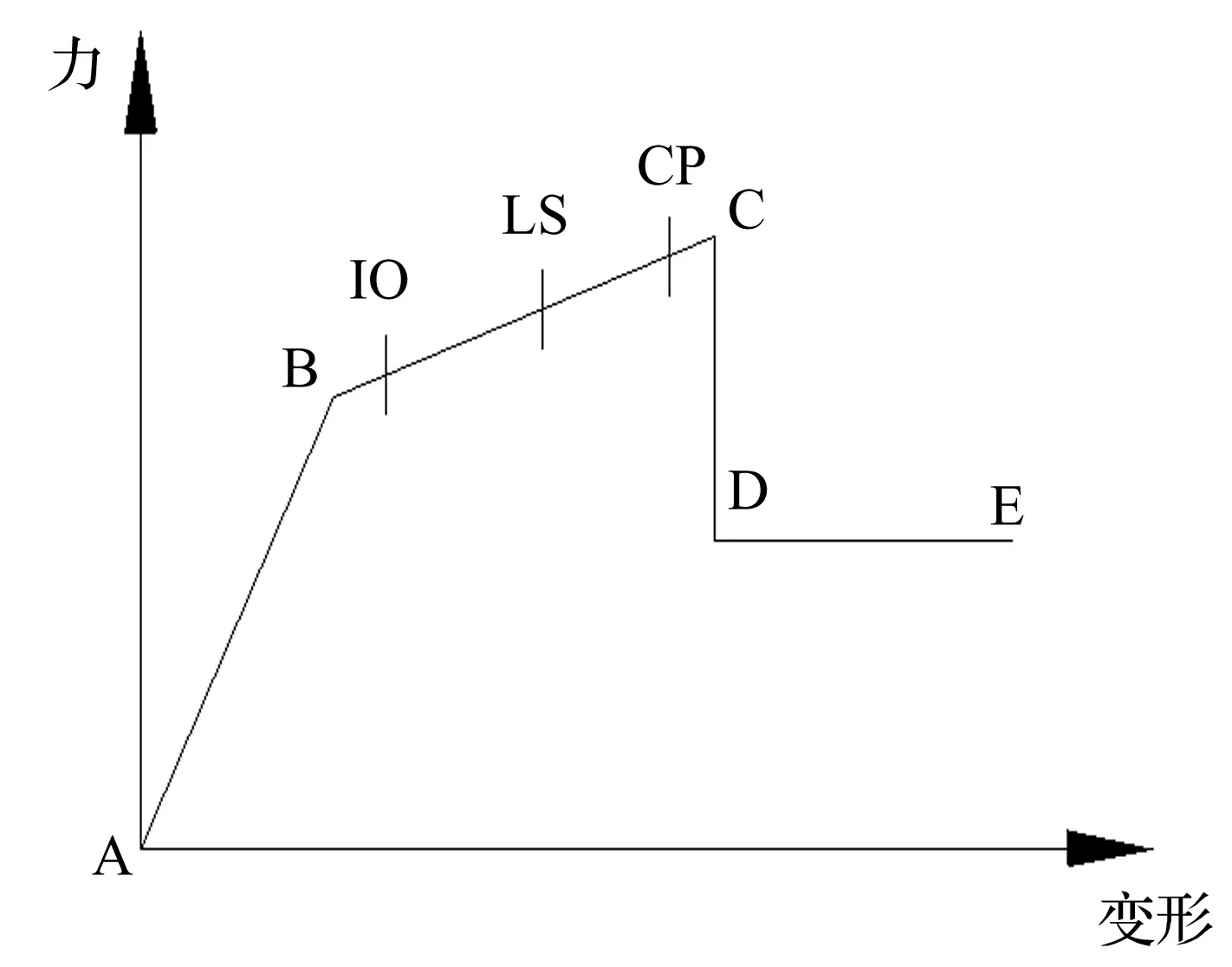
图5 在不同性能水准下的塑性铰位移限值

以底层框架柱失效导致底层失效破坏此时的加速度峰值作为时程计算工况，共得到20个工况。表1列出了不同地震波输入下结构失效时的加速度峰值。从表中可以看出，不同地震波输入下的加速度峰值差异较大，说明不同地震波输入所引起的结构地震反应有较大的差异。

表1 地震动输入工况

4 算例结构的地震损伤计算

4.1 各类构件的地震损伤计算

采用前文提出的构件损伤模型，可以计算得到各地震波工况下各楼层的框架梁、框架柱、核心筒剪力墙以及连梁各类构件的地震损伤指标，其中底层的计算结果如表2所示。

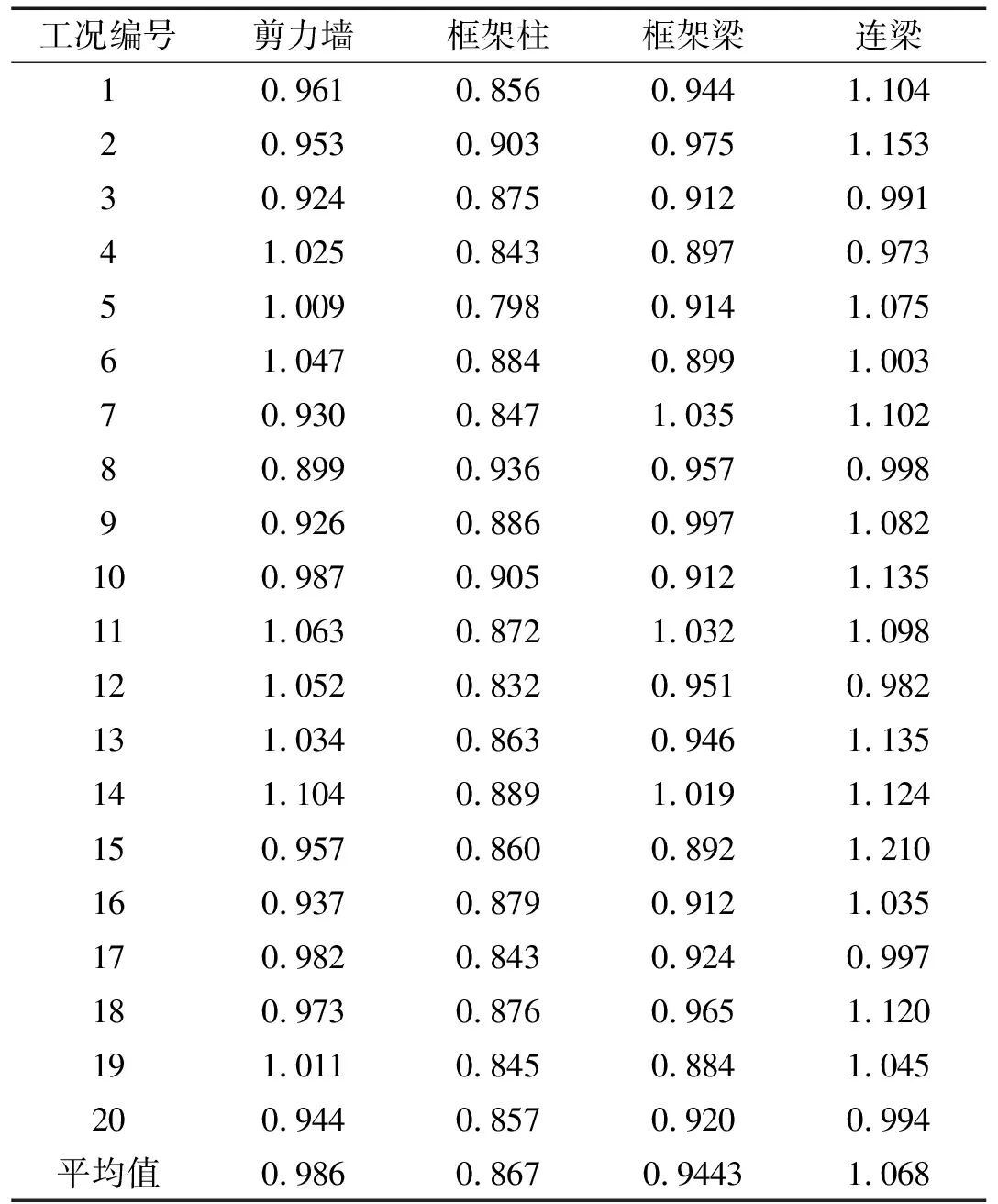
表2 各工况地震波输入下底层各类构件的加权损伤值

各个工况下，底层剪力墙、框架柱、框架梁和连梁的加权损伤值对比见图6所示。

图6 各工况地震波输入下底层各类构件的加权损伤值

可以看出，连梁的加权损伤值最大，说明连梁作为次要构件最先屈服消耗地震输入的能量并最先达到失效从而损伤最为严重。框架梁与剪力墙的加权损伤值次之，这主要是因为核心筒作为混合结构的第一道抗震防线，在地震作用下承担了大部分地震剪力，先于框架柱进入塑性状态，而框架的设计遵循了强柱弱梁的原则，框架梁也比较早地进入了塑性状态，加权损伤值也比较大。框架柱的加权损伤值最小，主要是因为：一方面框架作为第二道抗震防线，承担的地震剪力较小，破坏比较轻：另一方面，框架部分本身实现了“强柱弱梁”，即框架梁先进入屈服和破坏，而框架柱最后破坏。

同时列出了各工况地震波输入下25层、顶层各类构件的加权损伤值如图7、8所示。

对比图6和图7与图8，可以看出底层、25层与顶层各类构件的加权损伤值大小相对关系比较一致，连梁的加权损伤值最大，剪力墙和框架梁的加权损伤值次之，框架柱的加权损伤最小。这说明针对不同楼层，不同类型构件的加权损伤值相对大小关系是一致的，即不同楼层内各类构件的破坏顺序以及损伤程度相对大小都是一致的。总体而言，楼层位置越高，构件的地震损伤值越小。

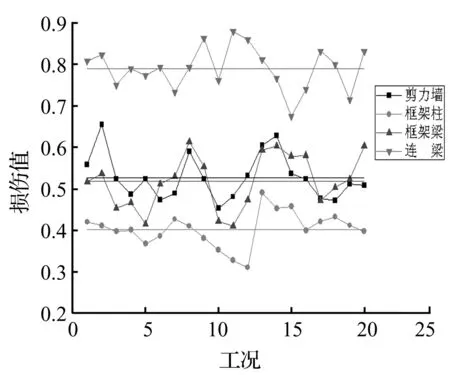
图7 各工况地震波输入下25层各类构件的加权损伤值

图8 各工况地震波输入下顶层各类构件的加权损伤值

4.2 各楼层的地震损伤计算

利用式(8)可计算得到各工况地震波输入下各楼层的地震损伤指标，其中工况2对应的地震波输入下的计算结果如表3所示。

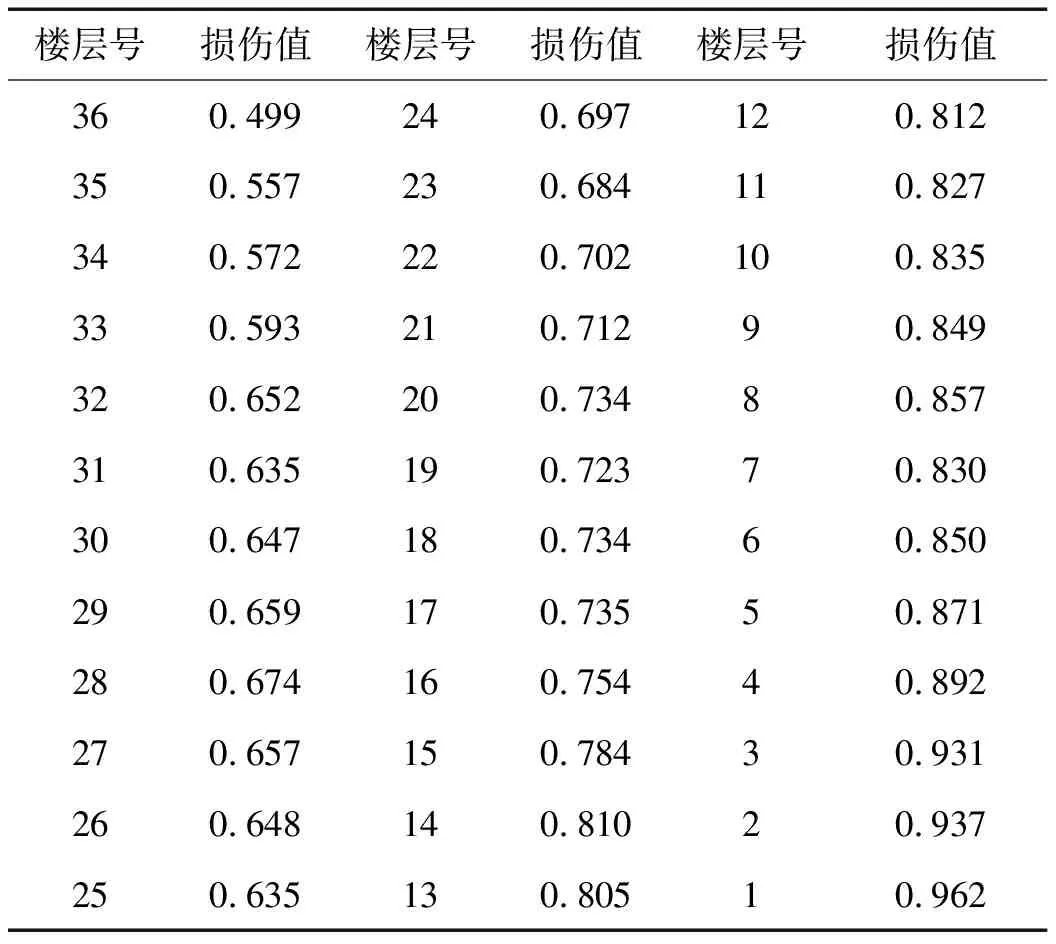
表3 工况2作用下各楼层的地震损伤指标

结合各楼层的损伤指标可以看出，总体而言，结构底部几层的损伤值较大，是结构的薄弱部位，结构的损伤值随楼层位置的上升有逐渐减小的趋势，但减小的幅度并不大，底层损伤值接近于1时，顶层损伤值在0.5左右。这是由钢-混凝土混合结构的特点决定的，可以从三个方面来解释：第一，核心筒剪力墙作为第一道防线承担了大部分的楼层剪力，在地震作用下首先屈服并消耗了地震输入的大部分能量，各个楼层的剪力墙均造成了较大的累积损伤，而从本文提出的楼层地震损伤模型可以看出，剪力墙对楼层的损伤贡献和影响最大，这样加权之后所得上部楼层的损伤值也比较大；第二，从结构的损伤发展情况来看，底层柱破坏时，上部楼层大部分框架梁都已失效，此时钢框架梁的损伤值也比较大；第三，连梁作为混合结构的理想耗能构件，最早进入了屈服状态，损伤值最大，虽然连梁损伤对楼层的损伤影响最小，但由于连梁本身损伤值比较大，所以它对楼层损伤值的贡献不可忽略。综合这三个方面原因，即使上部楼层的型钢混凝土框架柱损伤值比较小，按照本文损伤模型计算所得的楼层损伤值仍然比较大。

4.3 结构整体的地震损伤计算

按照本文提出的结构整体损伤模型计算了部分工况下结构的整体损伤指标，并与采用牛荻涛[7]提出的结构整体地震损伤模型计算得到的结果进行了比较，如表4所示。

从表4中可以看出，两种模型计算得到的结构整体的地震损伤指标比较接近，且各个工况下得到的结果也比较接近，结构失效时的整体损伤值离散性很小，其大小基本在0.8左右。因此，在应用本文提出的地震损伤模型进行钢-混凝土混合结构的性能等级划分时可将0.8作为结构整体失效的损伤指标限值。

表4 结构整体损伤指标比较

5 结 论

本文以型钢混凝土框架-混凝土核心筒结构为研究对象，对典型超高层钢-混凝土混合结构的地震损伤模型进行了研究。根据这类结构的地震损伤特点和损伤演化规律提出了构件、楼层、整体结构三个层次的地震损伤模型，可为钢-混凝土混合结构的地震损伤评估、基于性能的抗震设计提供依据。

参 考 文 献

[1]陈 敏.地震激励下混合结构中局部构件损伤对楼层整体损伤影响的研究[D].西安: 西安建筑科技大学,2010.

[2]熊仲明,史庆轩.钢筋混凝土框架结构倒塌破坏能量分析的研究[J].振动与冲击,2003,22(4): 8-1.

XIONG Zhong-ming,SHI Qing-xuan.Study on evaluation theory for collapse mechanism of reinforced concrete frame structure with energy method[J].Journal of Vibration and Shock,2003,22(4): 8-1.

[3]Houser G W.Limit design of structural to resist earthquakes [J].Proceedings of 1WCEE,1956,44-48.

[4]陈 鑫,阎 石,李 兵,等.高强钢筋高强混凝土柱损伤模型试验研究[J].工程力学,2013,(S1): 154-158.

CHEN Xin,YAN Shi,LI Bin,et al.Experimental study on damage model for HSC columns [J].Engineering Mechanics,2013,(S1): 154-158.

[5]侯圣吉.型钢高强高性能混凝土框架柱地震损伤模型研究[D].西安: 西安建筑科技大学,2009.

[6]Park Y J,Ang A H S,Wen Y K.Seismic damage analysis of reinforced concrete building[J].Journal of Structural Engineering,ASCE,1985,111(4): 740-757.

[7]牛荻涛.基于弹塑性随机动力分析的抗震结构概率设计理论与方法[D].哈尔滨：哈尔滨建筑工程学院,1991.

[8]刘良林,王全凤,林煌斌.基于周期的结构整体地震损伤评价方法[J].华侨大学学报(自然科学版),2013,03: 313-315.

LIU Liang-lin,WANG Quan-feng,LIN Huang-bin.Structural overall seismic damage evaluation method based on period [J].Journal of Huaqiao University (Natural Science),2013,3: 313-315.

[9]罗 欣,梁兴文,邓明科等.高强混凝土剪力墙地震损伤模型分析[J].地震工程与工程振动,2012,32(4): 145-151.

LUO Xin,LIANG Xing-wen,DENG Ming-ke,et al [J].Earthquake Engineering and Engineering Vibration,2012,32(4): 145-151.

[10]王东升,司炳君,艾庆华,等.改进的Park-Ang地震损伤模型及其比较[J].工程抗震与加固改造,2005,(S1): 144-150.

WANG Dong-sheng，SI Bing-jun，AI Qing-hua,et al.A comparative study of modified Park-Ang model and Park-Ang model for structural seismic damage evaluation [J].Earthquake Resistant Engineering and Retrofitting,2005,(S1): 144-150.

[11]刘 阳,郭子雄,黄群贤.型钢混凝土柱的损伤模型试验研究[J].武汉理工大学学报,2010,30 (9): 203-207.

LIU Yang,GUO Zi-xiong,HUANG Qun-xian.Experimental study of damage model for SRC columns [J].Journal of Wuhan University of Technology,2010,30(9): 203-207.

[12]Chai Y H,Romstad K M,Bird S M.Energy-based linear damage model for high-intensity seismic loading [J].Journal of Structural Engineering,1995,121(5): 857-864.

[13]陈林之,蒋欢军,吕西林.修正的钢筋混凝土结构Park-Ang损伤模型[J].同济大学学报,2010,38(8): 1103-1107.

CHEN Lin-zhi,JIANG Huan-jun,LÜ Xi-lin.Modified Park-Ang damage model for reinforced concrete structures[J].Journal of Tongji University,2010,38(8): 1103-1107.

[14]杜修力,欧进萍.建筑结构地震破坏评估模型[J].世界地震工程,1991,7(3): 50-58.

DU Xiu-Li,OU Jin-ping.Seismic damage assessment model of building structures [J].World Information on Earthquake Engineering,1991,7(3): 50-58.