TMD-基础隔震混合控制体系在近场地震作用下的能量响应与减震效果分析

王亚楠， 李 慧,2， 杜永峰,2

(1.兰州理工大学 防震减灾研究所，兰州 730050；2.兰州理工大学 西部土木工程防灾减灾教育部工程研究中心，兰州 730050)

基础隔震结构通过在上部结构和基础之间设置水平刚度明显小于上部结构抗侧刚度的隔震层来延长结构的基本周期，使上部结构与输入地震动的短周期成分几乎绝缘，最终达到保护上部结构的目的。地震作用下隔震结构的变形主要集中在隔震层，为了避免在强震作用下由于隔震层的位移过大而导致隔震垫破坏的情况发生，在进行隔震设计时经常采用下述两种措施：一种是在隔震层增设阻尼器，另一种是在隔震层设置限位器。这些措施虽然可以有效地控制隔震层位移，但往往会导致上部结构层间位移和峰值绝对加速度增大。

正是由于上述两种措施存在着不足，且工程上急需保证隔震垫在地震作用下的正常工作，Palazzo等[1-2]提出了一种将TMD和基础隔震技术联合起来进行控振的策略，并对安装有TMD的基础隔震结构在确定性地震激励和随机地震激励下的动力响应进行了分析。朱宏平等[3]对高层基础隔震结构和TMD相结合的混合控制体系在EL Centro地震波作用下的振动波和功率流大小进行了计算，结果表明：这种被动混合控制系统能够非常有效地抑制强地面运动作用下高层建筑的振动，而且明显降低了基础隔震系统内部的振动功率流。Melkumyan[4-5]首次将TMD应用于隔震住宅的设计当中，用来减小隔震结构的位移需求。De Iuliis等[6]对在隔震层安装TMD的摩擦摆基础隔震结构进行了非线性时程分析，研究了TMD用于减小隔震层地震响应的有效性。Tomoyo等[7]将安装有TMD的基础隔震结构简化为两自由度线性体系，采用随机方法求解了用于TMD设计的最优参数，主要对远场地震作用下TMD对基础隔震结构位移需求的影响进行了研究，研究结果表明：通过安装TMD，基础隔震结构的位移需求获得了15%～25%的减小。

上述研究者们主要针对远场地震作用下，假定上部结构和隔震层为弹性时，TMD对基础隔震结构地震响应的影响进行分析，并将安装TMD前后隔震层位移的比值作为衡量TMD减震效果的标准。但是，与远场地震相比，近场地震的特点非常显著，具有很高的加速度峰值和长周期的速度脉冲分量，巨大的地震能量以速度脉冲的方式输入结构，使结构发生弹塑性变形，最终给结构造成严重地破坏[8-9]。文中对近场地震作用下，考虑隔震层的非线性变形行为，安装TMD前后基础隔震结构的地震响应和能量响应进行求解，通过对结构中地震输入能量的传递和耗散过程的分析，从能量的角度来探讨TMD-基础隔震混合控制体系的减震效果。

1 运动方程及其求解

1.1 隔震支座非线性模型

文中对具有铅芯橡胶隔震支座(LRB)的TMD-基础隔震混合控制体系进行研究。采用Bouc-Wen模型来描述铅芯橡胶隔震支座的非线性力-变形行为，那么隔震支座的恢复力可表示为[10]：

(1)

(2)

式中:q为LRB的屈服位移；γ，β，η和A为滞回环的无量纲参数。α，β，γ，η和A对滞回环的形状起控制作用，通常情况下由实验确定。

LRB的屈服后刚度αkb与隔震结构的设计周期Tb相关联，其中Tb可以表示为：

(3)

式中:M为隔震结构的总质量。

隔震垫中由橡胶部分产生的粘性阻尼cb可以通过橡胶部分的阻尼比ξb来求解，即：

cb=2Mωbξb

(4)

式中:ωb=2π/Tb为隔震结构的频率。

1.2 TMD最优参数求解

文献[11]基于优化设计的方法给出了地震作用下以主结构位移最小作为目标函数的TMD最优参数的求解公式：

(5)

(6)

式中:fopt为TMD自振频率与隔震结构自振频率的最佳比值；ξopt为TMD的最佳阻尼比；μ为TMD质量与隔震结构总质量的比值。所需的TMD参数根据上述两式进行求解。

1.3 运动方程建立及其求解

如图1所示的层间剪切型混合控制体系，其运动方程可表示为：

(7)

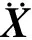
F=KX+H(1-α)FyZ

(8)

式中:K为体系的刚度矩阵；X为体系的相对位移列向量；H=[1,0,…,0]T为隔震层位置向量:

(9)

式中:k1，k2,…,kn为上部结构各层的刚度；kT为TMD的刚度。

将式(8)代入式(7)并联立式(2)，采用状态空间描述法将运动方程改写成一阶微分方程的形式，即：

(10)

式中:

运用四阶龙格-库塔方法[14]对该微分方程进行迭代求解。

图1 TMD-基础隔震混合控制体系

2 能量平衡方程及其求解

对式(7)两边关于相对位移列向量X进行积分，得到体系的相对能量平衡方程：

(11)

式中:左边第一项代表体系动能EK，第二项代表体系阻尼耗能ED，第三项由体系的弹性应变能ES和隔震支座滞回耗能EH组成；等式右边项代表体系输入能EI。

(12)

(13)

(14)

(15)

(16)

任意时刻t，体系各项能量之和与地震动输入能保持平衡，即：

EK+ED+ES+EH=EI

(17)

采用牛顿-科斯特公式[14]中的梯形法则对式(12)～式(16)进行求解，然后根据式(17)判断其误差大小。

3 数值算例

3.1 工程概况

以某上部结构8层的基础隔震结构为例，上部结构各层质量mi=2.3×105kg(i=1,2…8)，各层刚度ki=3.9×108N/m(i=1,2…8)，阻尼比ξs=0.05；隔震层质量mb=3.3×105kg，隔震层刚度kb=1.9×107N/m，隔震支座的粘性阻尼比ξb=0.05，隔震支座的屈服位移q=0.015 m，隔震支座屈服后与屈服前的刚度比α=0.1。用于描述隔震支座非线性行为的Bouc-Wen模型的相关参数β，γ，η，A的取值分别为0.5，0.5，1，1；TMD的相关参数包括TMD的质量、刚度以及阻尼比，当质量比μ=0.1时，TMD的质量mt=2.2×105kg，通过式(5)和式(6)可求得TMD的相关参数fopt=0.89，ξopt=0.15。

3.2 近场地震动选取

选取具有不同脉冲周期的四条近场地震记录，如表1所列，脉冲周期[15]的范围大致可以覆盖基础隔震结构的基本周期范围，计算时，所有地震动的加速度峰值均调幅为400 cm/s2。

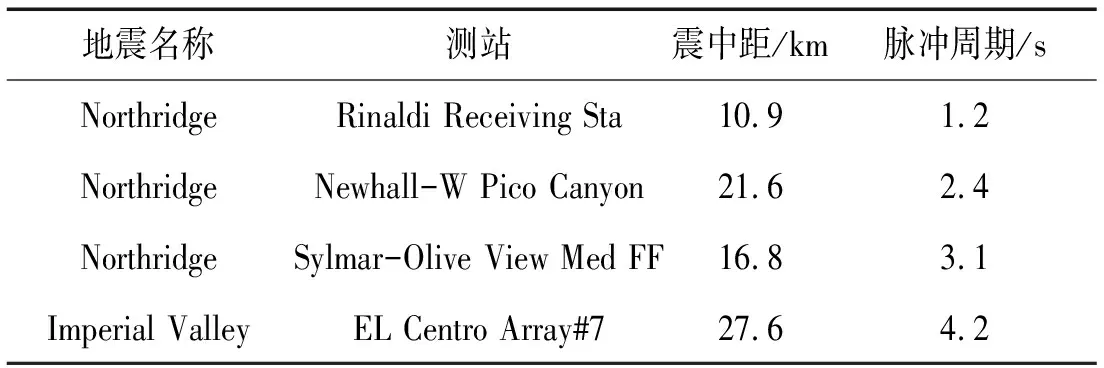
表1 近场地震动记录

3.3 非线性时程分析

图2为脉冲周期为2.4 s的近场地震动作用下，安装TMD前后隔震层的位移响应对比。可以看出，TMD对隔震层位移的第一峰值没有起到控制作用，对第二位移峰值有明显的控制效果，其中第一、第二峰值是根据其出现时刻的先后顺序来定义的。

不同脉冲周期的地震动作用下，安装TMD前后隔震层位移响应的第一、第二峰值对比如表2所示，可以看出在不同脉冲周期的地震动作用下，TMD对隔震层位移的第一峰值的减震作用均不明显，某些地震动作用下有轻微的放大作用，但控制在10%以内，而对第二峰值具有明显的减震效果，其中当脉冲周期Tp与结构基本周期接近时(Tp=2.4 s)，减震效果最为明显，减小了约54%，当脉冲周期远离结构基本周期时，减震效果有所降低。

同时从表2可以看出隔震层位移的最大峰值响应可能与第一峰值对应，也可能与第二峰值相对应，这与地震动特性有关，因此如果仅以隔震层最大位移作为控制目标来衡量TMD的减震效果，它的有效性就大大地弱化了，这与文献[6]所得的结论一致。

表2 安装TMD前后隔震层位移峰值对比

3.4 能量响应分析

图3和图4分别为脉冲周期为2.4s的近场地震动作用下，原结构与混合控制体系的能量响应。从图3可以看出，当隔震层在强震作用下进入非线性变形阶段后，地震动输入原结构的能量主要通过隔震垫的滞回耗能和结构的阻尼耗能来耗散，其中滞回耗能占了很大的比重，因此起到了保护上部结构的作用。从图4可以看出，混合控制体系的能量也是通过隔震垫的滞回耗能和体系的阻尼耗能来耗散掉，但是两者所占的比重大致相同，说明在混合控制体系中阻尼耗能同样发挥了很大的作用。

结合图3和图4可以看出，基础隔震结构和混合控制体系的输入能在后期主要通过隔震层滞回耗能和阻尼耗能来耗散，动能和应变能仅占很少一部分，因此文中主要通过分析结构的输入能、隔震层滞回耗能以及阻尼耗能的变化来研究TMD对结构的控制效果。

图2 隔震层位移响应对比

图5～图7分别为脉冲周期为2.4 s的近场地震动作用下，原结构与混合控制体系的输入能对比、阻尼耗能对比和隔震层滞回耗能对比。从图5可以看出，混合控制体系的输入能要大于原结构的输入能，究其增大原因，从式(15)可以看出体系的输入能与体系的质量、地震动加速度以及体系的速度响应相关联，安装TMD后不仅增加了结构的质量而且体系的振动特性也与原结构有所不同。从图6和图7可以看出，与原结构相比混合控制体系的阻尼耗能明显增加，隔震层的滞回耗能明显减小。这些结果表明在混合控制体系中更多的输入能由阻尼耗散掉，从而减小了隔震垫的滞回耗能，对隔震垫起到了保护的作用。

图5 原结构与混合控制体系输入能对比

为了研究TMD对基础隔震结构的控制效果，将混合控制体系的能量响应分解成TMD(子结构)和基础隔震结构(主结构)的能量响应两部分。主结构的能量响应包括主结构动能、弹性应变能、阻尼耗能以及隔震层滞回耗能，文中将它们的和值称之为主结构输入能；子结构的能量响应包括TMD的动能、应变能和阻尼耗能。

图8和图9为脉冲周期为2.4s的近场地震动作用下，安装TMD前后主结构的输入能对比和阻尼耗能对比，主结构的隔震层滞回耗能对比如图7所示。从图8和图9可以看出，安装TMD后主结构的输入能和阻尼耗能都明显地减小，结合图6可知体系中阻尼耗能的增加是由TMD的阻尼耗能引起的。因此从能量的角度来看，TMD通过自身的阻尼耗能消耗了体系的大部分输入能，从而减小了主结构的能量响应。

同时从图8和图9可以看出，在初始时段TMD对主结构能量响应的控制效果很微弱，在后期达到稳定状态，这表明TMD减震效果的发挥有一定的滞后性，它的耗能作用的发挥需要一个储存能量的过程来使它运动起来，这也是TMD对隔震层位移第一峰值几乎没有起到控制作用的原因。

图8 安装TMD前后主结构输入能对比

图9 安装TMD前后主结构阻尼耗能对比

不同脉冲周期地震动作用下，安装TMD前后主结构的输入能峰值、隔震层滞回耗能峰值以及阻尼耗能峰值对比见表3～表5。

表3 主结构输入能峰值对比

从表3可以看出，在不同脉冲周期地震动作用下，安装TMD后主结构的输入能都减小了，但减小的幅度受脉冲周期的影响较大，变化范围从13%到28%，因此在实际工程中选取TMD参数时应考虑到地震动特性的影响。

从表4可以看出，安装TMD后隔震层的滞回耗能明显减小，说明隔震层的非线性变形得到了一定程度的控制。减小的幅度同样受到脉冲周期的影响，当脉冲周期与结构基本周期接近时控制效果最好，减小了约35%。

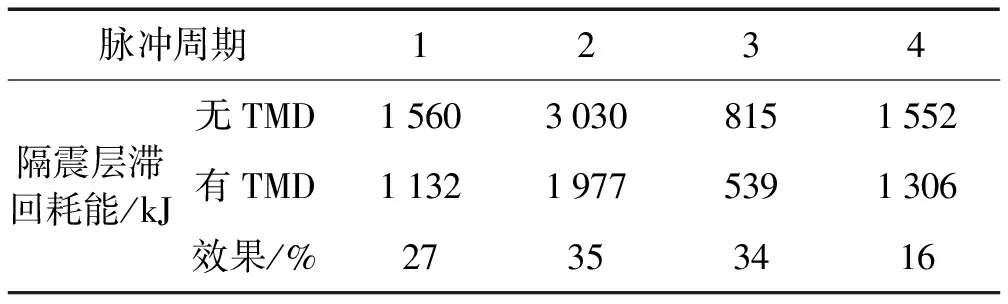
表4 主结构隔震层滞回耗能峰值对比

从表5可以看出，在不同脉冲周期地震动作用下，主结构的阻尼耗能都减小了，这就更进一步的说明主结构能量响应的减小主要是由TMD的阻尼耗能引起的，主结构阻尼耗能的减小程度同样受到脉冲周期的影响。

表5 主结构阻尼耗能峰值对比

4 结 论

文中对近场地震作用下TMD-基础隔震混合控制体系的非线性地震响应和能量响应进行了求解，分析了不同脉冲周期地震动下体系的能量变化和耗散过程，最后对其减震效果进行了研究，得出以下主要结论：

(1)TMD对隔震层位移第一峰值几乎没有起到控制作用，而对第二峰值的控制效果明显，因此如果以隔震层位移峰值的最小化作为控制目标，安装TMD后的控制效果并不理想。

(2)安装TMD后，主结构的输入能和隔震层的滞回耗能有较大程度的减小，这是因为TMD中的阻尼耗散了体系中大部分的输入能。同时TMD减震作用的发挥有一定的滞后性，因为它需要一个储存能量的过程。

(3)当脉冲周期与结构的基本周期接近时，TMD的减震效果最好，当脉冲周期逐渐偏离结构基本周期时，减震效果有所降低，因此在选取TMD的参数时，应考虑地震动特性的影响。

参 考 文 献

[1]Palazzo B,Petti L.Seismic response control in base isolated systems using tuned mass dampers [C]// Proceedings of First World Conference on Structural Control.Los Angeles,California,1994.

[2]Palazzo B,Petti L,De Ligio M.Response of base isolated systems equipped with tuned mass dampers to random excitations [J].Journal of Structural Control,1997,4(1): 9-22.

[3]朱宏平,唐家祥.高层建筑被动混合控制的波动分析 [J].地震工程与工程振动,1998,18(3),56-66.

ZHU Hong-ping,TANG Jia-xiang.A traveling wave approach to seismic passive combined control system of tall buildings[J].Earthquake Engeering and Engineering Vibration,1998,18(3): 56-66.

[4]Melkumyan M G.The state-of-the-art in structural control in armenia and proposal on application of the dynamic dampers for seismically isolated buildings [C]// In: Proceedings of the Third International Workshop on Structural Control for Civil and Infrastructure Engineering,2000.

[5]Melkumyan M G.First application of the dynamic damper in the design of seismically isolated dwelling house [C]// In: Lesch R,IrschikH,KrommerM,editors,Proceeding of the third European conference on structural control,2004.

[6]De Iuliis M,Petti L,Palazzo B.Combined control strategy base isolation and tuned mass damper: an effectiveness analysis of its application to nonlinear benchmark base isolated structure [C]// The 14th World Conference on Earthquake Engineering.Beijing,China,2008.

[7]Taniguchi T,Kiureghian A D,Melkumyan M.Effect of tuned mass damper on displacement demand of base-isolated structures [J].Engineering Structures,2008,30: 3478-3488.

[8]江 辉,朱 晞.脉冲型地震动模拟与隔震桥墩性能的能量分析 [J].北方交通大学学报,2004,28(4): 6-11.

JIANG Hui,ZHU Xi.Simulation of pulse-type earthquake excitation and energy performance of isolated bridge piers [J].Journal of Northern JiaoTong University,2004,28(4): 6-11.

[9]Li H,Wang Y A,Du Y F.Vibration control of hybrid control system of TMD-Base isolation under near-fault seismic ground motions[R].International Conference on Computer and Information Science,Safety Engineering,2012,1119.

[10]Jangid R S.Stochastic response of building frames isolated by lead-rubber bearings [J].Struct.Control Health Monit,2010,17:1 22.

[11]Bakre S V,Jangid R S.Optimum parameters of tuned mass damper for damped main system [J].Struct.Control Health Monit,2007,14: 448-470.

[12]Clough R W,Penzien J.Dynamics of structures [M].McGraw-Hill,Inc,1993.

[13]杜永峰,李 慧,Spencer B F,等.非比例阻尼隔震结构地震响应的实振型分解法 [J].工程力学,2003,20(4): 24-31.

DU Yong-feng,LI Hui,Spencer Billie F,et al.Real mode superposition method for analysis of seismic response of non-proportionally damped isolated structures[J].Engineering Mechanics,2003,20(4): 24-31.

[14]唐玲艳,田尊华.工程与科学数值方法的MATLAB实现[M].北京: 清华大学出版社,2009.

[15]Baker J W.Quantitative classification of near-fault ground motions using wavelet aanlysis [J].Bulletin of the Seismological Society of America,2007,97(5): 1486-1501.