大跨径桥梁静风稳定参数的敏感性分析
2014-09-05李加武侯利明
李加武,方 成,侯利明,汪 洁
(1.长安大学 公路学院,西安 710064;2.中交第一公路勘察设计研究院有限公司,西安 710055;3.西安建筑科技大学,西安 710055)
与动力失稳不同,静力失稳发生前无任何预兆,具有突发性强、破坏性大的特点。过去,人们普遍认为大跨径桥梁的颤振临界风速一般都低于静力失稳的发散风速。但是,1967年,日本东京大学Hirai教授在悬索桥的全桥模型风洞试验中观察到了静力扭转发散现象。同济大学风洞试验室在汕头海湾二桥的风洞试验中,发现了斜拉桥由静风引起的弯扭失稳现象。后来,Boonyapinyo等学者对桥梁静风稳定性问题进行不断的探讨和改进,初步探明了失稳机理。在总结已有研究的基础上,本文基于风洞试验测得的主梁静力三分力系数,在综合考虑结构几何非线性和静风荷载非线性的基础上,对大跨径悬索桥以及大跨径斜拉桥进行了静风失稳全过程分析;然后分别考察了三分力系数、初始风攻角、桥塔风荷载、缆索风荷载以及边跨风荷载等参数对大跨径缆索承重桥静风稳定性的敏感程度,得出在分析中必须考虑的参数和可以忽略的参数,为大跨径桥梁的抗静风设计提了供依据与参考。
1 静风稳定性分析程序实现
静风失稳的临界风速是通过三分力系数的欧几里得范数来判断,本文基于大跨径桥梁静风稳定性理论,在程进等人提出的增量与内外两重迭代相结合的基础上,引入外层迭代次数上限与风速步长,利用ANSYS编制了相应的参数化程序,其具体实现步骤如下:
(1)根据资料,在ANSYS中建立全桥三维有限元模型,并对模型进行自重荷载下的位移计算;
(2)提取主梁扭转角{θ}0,计算该状态下的三分力系数,此时主梁上的有效攻角均等于初始攻角α0;
(3)假定初始风速U0和初始风速步长DU0,当前风速Ui=U0,设定外层迭代次数上限Nmax;
(4)计算当前Ui风速下主梁的静风荷载,采用Newton-Rapson方法进行结构非线性求解,获得收敛解(内层迭代);
(5)提取主梁扭转角向量{θ}i,则该级风速下用于修正三分力系数的扭转角向量取{q}i={q}i+j{Dq}i,其中,φ为松弛因子,在0~1.0之间,本文取0.35。扭转角增量{Dq}i={q}i-{q}i-1-j{Dq}i-1,此时,主梁的有效攻角{α}={α0}+{q}i;
(6)计算该状态下的三分力系数;
(7)检查三分力系数的欧几里得范数是否小于允许值;

(k=X,Y,Z)
式中:Na为受到静风荷载作用的主梁节点总数;Ck为阻力、升力或升力矩系数;epsk为阻力、升力或升力矩系数的允许误差,一般在0.000 5~0.005之间取值。
(8)如果三分力系数的范数全小于允许值,说明本级风速计算结果收敛,输出计算结果。按设定步长增加风速,返回步骤(4)进行下一级风速计算(增量法);
(9)如果三分力系数的范数大于允许值,重复步骤(4)~(7)(外层迭代)。若迭代次数达到迭代次数上限,说明本级风速难以收敛,则恢复到上一级风速状态,将风速步长减半,返回步骤(4),重新计算。如果风速步长小于预定值,计算结束;
(10)绘制结构变形-风速曲线,判定静风失稳临界风速。
其计算流程图见图1。
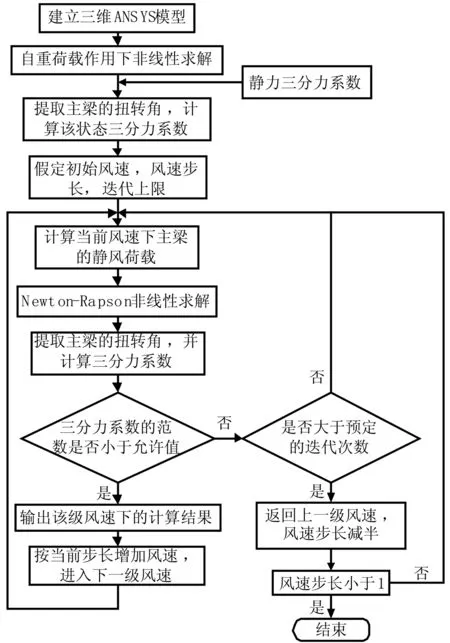
图1 静风稳定性计算流程图
2 虎门二桥概况及计算模型
虎门二桥位于广东省珠江三角洲地区,西起广州市番禺区东涌镇,接珠三角经济区环形公路南环段和京珠高速公路,终于东莞市厚街互通立交,与广深高速相交,东接正在规划中的厚街至寮步高速公路。虎门二桥工程主桥桥位南距虎门大桥约10 km,北距珠江黄埔大桥约20 km,连续跨越大沙水道和坭洲水道。该项目分为过江通道工程和接线工程,过江通道工程由坭洲水道桥、大沙水道桥和引桥组成,坭洲水道桥采用主跨(658+1 688)m双塔双跨扁平箱梁悬索桥,大沙水道桥采用主跨1 200 m双塔单跨悬索桥或斜拉桥,引桥采用40-60 m预应力混凝土桥。坭洲水道桥和大沙水道桥的有限元计算模型分别如图2和图3所示。

图2 坭洲水道桥有限元计算模型

图3 大沙水道桥有限元计算模型
3 静风稳定性参数的敏感性分析
3.1 三分力系数的影响
主梁静力三分力系数是描述主梁静风荷载的一组无量纲参数,不同的主梁断面有不同的三分力系数。本节对坭洲水道桥的主梁断面进行了更换,分别选取坭洲水道桥方案一主梁断面,方案三主梁断面及大沙水道桥主梁断面,其它结构参数保持不变,计算该桥的静风失稳临界风速。通过计算得到不同主梁静力三分力系数下静风失稳临界风速值如表1所示。洲水道桥方案一主梁断面,方案三主梁断面及大沙水道桥主梁断面如图4~图6;主梁最大竖向位移、侧向位移和扭转变形随风速的变化如图7~图9所示;图10~图12分别为三个主梁断面的升力系数、阻力系数和升力矩系数比较图。

表1 不同静力三分力系数下静风失稳临界风速

图4 坭洲水道桥方案一主梁断面
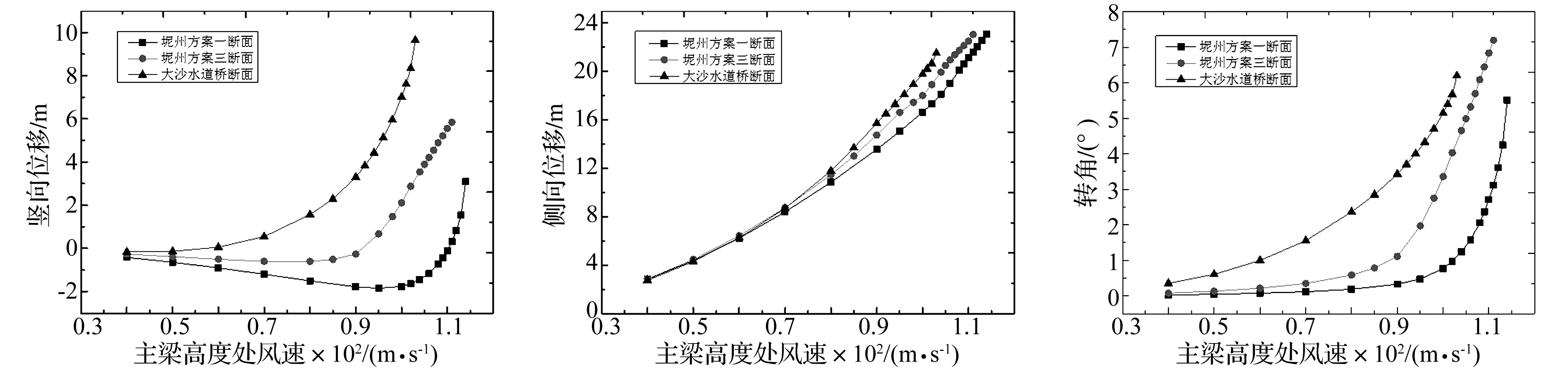
图7 主梁最大竖向位移随风速的变化
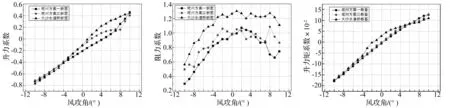
图10 升力系数比较图
从图7~图12中可以看出,坭洲水道桥方案一与方案三主梁的升力系数和升力矩系数较为接近,计算所得的静风失稳临界风速仅差3 m/s,约占失稳风速的2.6%,而坭洲水道桥方案一与大沙水道桥主梁的升力系数和升力矩系数相差大,静风失稳临界风速相差达到了11 m/s,约占失稳风速的9.7%。因此,主梁的三分力系数值是影响结构静风稳定性的主要因素之一,其中升力系数和升力矩系数对静风稳定性影响较大。
3.2 初始风攻角的影响
桥梁结构的有效攻角是由风的初始攻角和主梁的扭转角两部分组成的,而结构所承受静风荷载的大小又是结构有效攻角的函数,不同的初始风攻角势必会影响到结构的静风荷载大小。本节选取风的初始攻角为0°、+1°、+2°、+3°(因负攻角对结构的静风稳定性起到有利的作用,故没有选取)分别对坭洲水道桥的静风失稳临界风速进行了计算与比较。得到各初始风攻角下的静风失稳临界风速值如表2所示。图13~图15为主梁最大竖向位移、侧向位移和扭转变形随风速变化的对比图。

表2 不同初始攻角下静风失稳临界风速
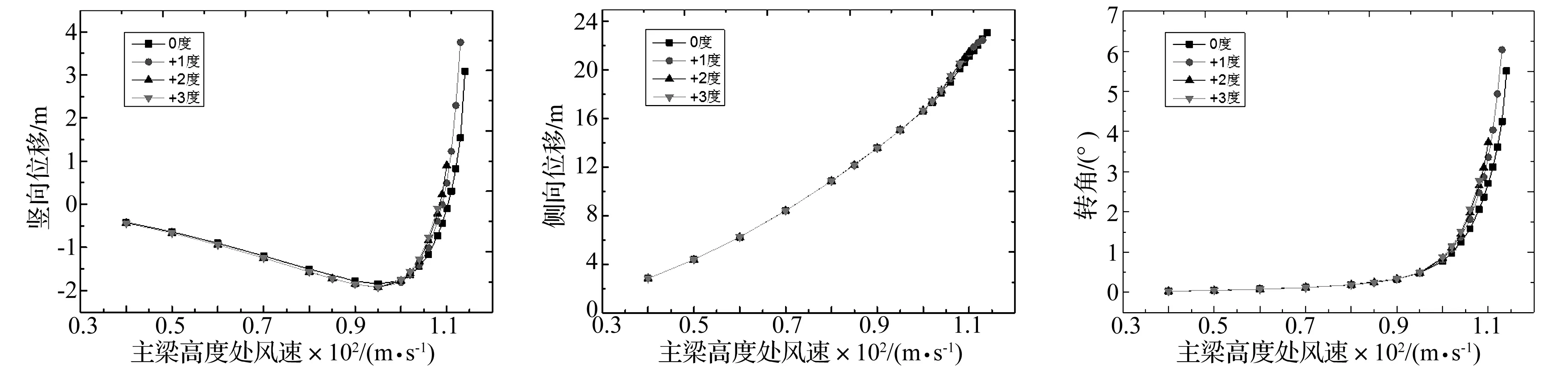
图13 主梁最大竖向位移随风速变化的对比
从图13~图15中可以看出,随着风速的不断增加,主梁的竖向位移、侧向位移和扭转角的变化趋势基本相同,但静风失稳临界风速值随着初始风攻角的增加而逐渐减小,最大相差6 m/s,约占失稳风速的5.6%,因此坭洲水道桥初始风攻角的选取对静风稳定性的影响较大。初始风攻角对静风稳定性的影响大小主要与主梁静力三分力系数有很大关系,主梁的升力系数和升力矩系数变化越快,对静风稳定性的影响也就越大。
3.3 桥塔风荷载的影响
大跨度缆索承重桥的桥塔一般都较高且迎风面积较大,其上作用的静风荷载与迎风面积成正比,与桥塔基准高度处的风速平方成正比,因此桥塔静风荷载相对较大, 本节分别对坭洲水道桥和大沙水道桥的桥塔加风荷载与不加风荷载进行了分析。经过计算,得到坭洲水道桥和大沙水道桥桥塔加风荷载与不加风荷载时的静风失稳临界风速值见表3所示。图16~图18为坭洲水道桥主梁最大竖向位移、侧向位移和扭转变形随风速变化的对比图,图19~图21为大沙水道桥主梁最大竖向位移、侧向位移和扭转变形随风速变化的对比图。

表3 桥塔风荷载对临界风速的影响
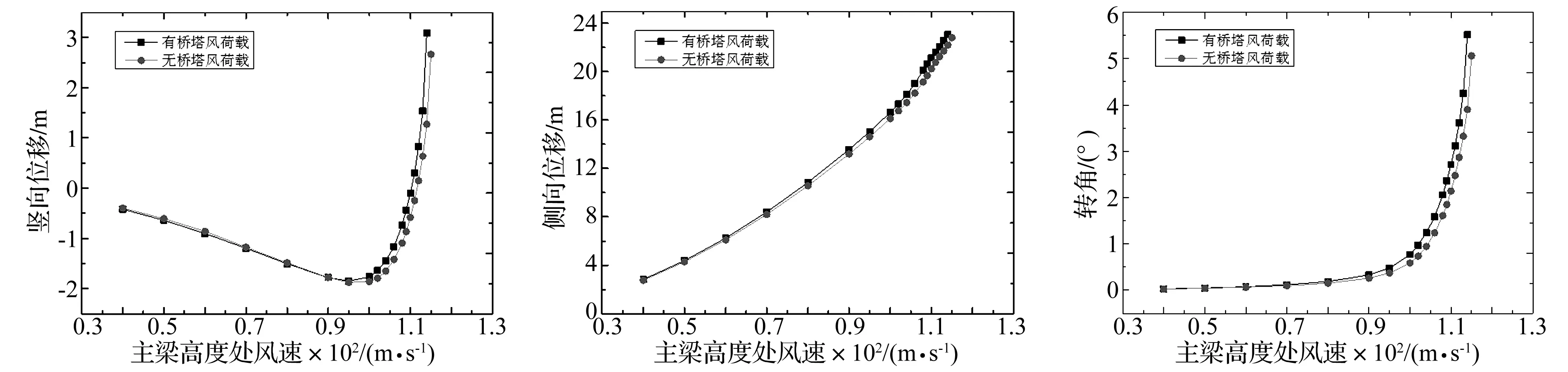
图16 坭洲水道桥竖向位移随风速的变化
图19 大沙水道桥竖向位移随风速的变化
从图16~图18中可以看出,随着风速的不断增加,坭洲水道桥主梁的竖向位移、侧向位移、扭转角的变化曲线基本重合,桥塔加风荷载与不加风荷载的静风失稳临界风速值仅差1 m/s,约占失稳风速的0.9%,因此悬索桥桥塔风荷载对结构静风稳定性影响很小,可以被忽略。
从图19~图21中可以看出,随着风速的不断增加,大沙水道桥主梁的竖向位移、侧向位移、扭转角的变化曲线基本重合,桥塔加风荷载与不加风荷载的静风失稳临界风速值仅差3 m/s,约占失稳风速的1.5%,因此斜拉桥桥塔风荷载对结构静风稳定性影响很小,可以被忽略。
3.4 主缆及吊杆风荷载的影响
随着悬索桥跨径的不断增大,其主缆和吊杆的直径将相应加大,使得主缆和吊杆上的风荷载也随之变大。坭洲水道桥的主缆直径达到了0.93 m,吊杆的直径为0.074 m,主缆和吊杆上的风荷载有可能对桥梁结构的静风稳定性产生一定的影响。为了考察主缆和吊杆上的风荷载对结构静风稳定性的影响,下面分以下四种情况进行计算:
(1)施加所有风荷载;
(2)不施加吊杆风荷载;
(3)不施加主缆风荷载;
(4)主缆和吊杆风荷载都不施加;
四种情况下静风失稳临界风速如表4所示。图22~图24为主梁竖向位移、侧向位移和扭转变形随风速的变化。

表4 不同情况下静风失稳临界风速

图22 主梁竖向位移随风速的变化
由图22~图24可以看出,情况一和情况二计算得到的静风失稳临界风速相差很小,仅差1 m/s,约占失稳风速的0.9%,而情况一和情况三计算的静风失稳临界风速相差11 m/s,约占失稳风速的9.6%,即吊杆风荷载对结构的静风稳定性影响较小,主缆风荷载对结构的静风稳定性影响较大,而且加主缆风荷载对结构的静风稳定性产生不利的作用。
而且,从图22~图24可以看出,主缆风荷载对主梁的侧向位移,竖向位移和扭转角影响都较大,吊杆风荷载对三者的影响都很小。其主要原因是主缆的直径达到了0.93 m,每延米风荷载约为主梁横桥向风荷载的18%,吊杆的直径为0.074 m,每延米风荷载约为主梁横桥向风荷载的1.4%,因而主缆风荷载对结构的静风稳定性影响较大,载,因此,在大跨径悬索桥的静风稳定性分析中必须考虑主缆风荷载的作用,否则偏于不安全。
3.5 斜拉索风荷载的影响
大跨度斜拉桥的斜拉索相对较长,直径较大,作用在拉索上的风荷载相应也较大,并且斜拉索与主梁直接相连,其上的荷载会间接作用在主梁上,因此斜拉索上的风荷载可能对结构的静风稳定性产生一定的影响。本节对大沙水道桥的斜拉索分别加风荷载与不加风荷载进行计算,得到两种情况下结构的静风失稳临界风速值见表5所示。图25~图27为主梁最大竖向位移、侧向位移和扭转变形随风速变化的对比图。

表5 不同情况下静风失稳临界风速

图25 主梁最大竖向位移随风速变化
从图25~图27中可以看出,主梁的竖向位移、侧向位移及扭转角在风速不断增加的过程中相差较大,当达到静风失稳风速时,大沙水道桥加斜拉索风荷载的跨中主梁节点侧向位移达到20 m,不加斜拉索风荷载的跨中主梁节点侧向位移为13m,相差很大,而且在同一风速下,有斜拉索风荷载的主梁竖向位移、扭转变形都比没有斜拉索风荷载时大。两者的静风失稳临界风速值相差也较大,达到了12 m/s,约占失稳风速的6.2%。因此,在求解斜拉桥静风失稳临界风速时,斜拉索的风荷载不能忽略。
3.6 边跨风荷载的影响
大跨度斜拉桥边跨跨度相比主跨跨度较小,静风失稳时,最大位移一般都出现在主跨跨中,边跨的位移相对较小,边跨风荷载是否影响主跨位移和静风失稳临界风速不太清楚,本节对大沙水道桥边跨的主梁和斜拉索分别加风荷载与不加风荷载进行计算,得到两种情况下的静风失稳临界风速值见表6所示。图28~图30为主梁最大竖向位移、侧向位移和扭转变形随风速变化的对比图。
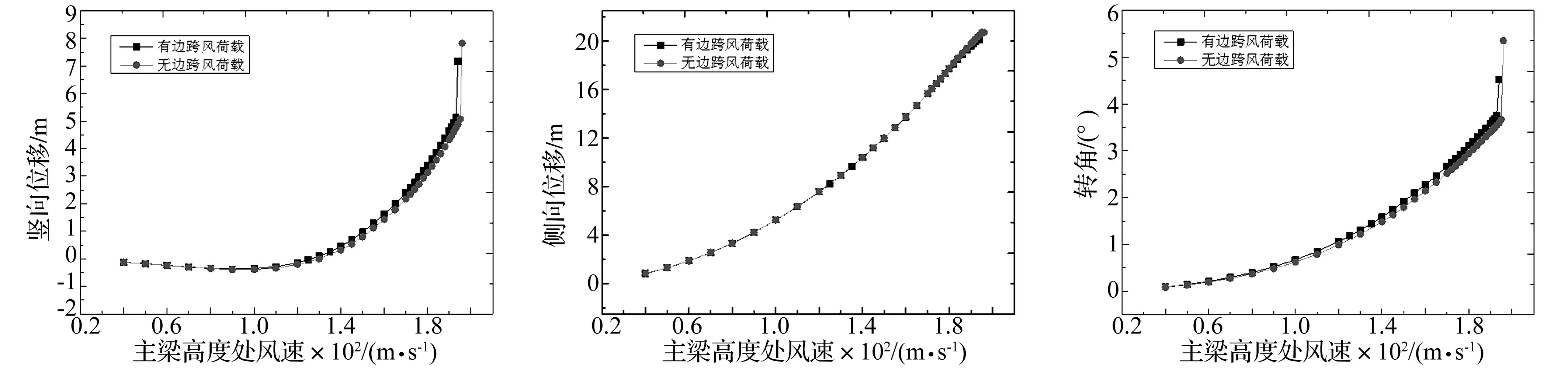
图28 主梁最大竖向位移随风速变化

表6 边跨有无风荷载情况下静风失稳临界风速
从图28~图30中可以看出,随着风速的不断增加,两种情况下主梁的竖向位移、侧向位移、扭转角的变化曲线基本重合,静风失稳临界风速仅相差2m/s,约占失稳风速的1%,因此边跨风荷载对桥梁静风稳定性的影响很小,可以被忽略。
4 结 论
本文以虎门二桥为例,通过改变影响静风稳定性的参数来考察其对大跨径缆索承重桥静风稳定性的敏感程度,分析计算结果可得如下结论:
(1)主梁静力三分力系数是影响桥梁静风稳定性的主要因素之一,其中升力系数和扭转力矩系数对静风稳定性影响较大;
(2)桥梁结构的静风稳定性一般随着初始风攻角的增加而降低,当升力和升力矩系数变化较快时,影响较大,变化较慢时,影响较小;
(3)桥塔风荷载对桥梁静风稳定性的影响很小,可以被忽略;
(4)大跨径悬索桥主缆风荷载对静风稳定性影响较大,分析中必须考虑,吊杆风荷载对静风稳定性影响很小,可以忽略;
(5)由于大跨径斜拉桥拉索一般较长,其上风荷载较大,且直接与主梁相连,拉索风荷载对静风稳定性影响较大,分析中不能忽略;
(6)边跨风荷载对桥梁静风稳定性的影响很小,可以被忽略。
参 考 文 献
[1]白 桦,李 宇,李加武.钢桁架悬索桥颤振稳定性能研究[J].振动与冲击,2013,32(4):90-95.
BAI Hua,LI Yu,LI Jia-wu,et al.Flutter stability of a steel truss girder suspension bridge[J].Journa l of Vibration and Shock,2013,32(4):90-95.
[2]丁泉顺,朱乐东.基于气弹模型试验的高耸结构随机风振等效静力风荷载[J].振动与冲击,2012,31(24):34-37.
DING Quan-shun,ZHU Le-dong.Equivalent static wind loads for stochastic vibration of a towering structure based on its aeroelastic-model wind tunnel test[J].Journal of Vibration and Shock,2012,31(24):34-37.
[3]Boonyapinyo V,Yamada H,Miyata T.Wind-induced nonlinear lateral-torsional buckling of cable-stayed bridges.Journal of Structural Engineering,ASCE,1994,120(2): 486-506.
[4]Larsen A.Advances in aeroelastic analysis of suspension and cable-stayed bridges[J].Journal of Wind Engineering and Industrial Aerodynamics,1998: 73-90.
[5]程 进,江见鲸,肖汝诚,等.大跨度桥梁空气静力失稳机理研究[J].土木工程学报,2002,35(1):35-39.
CHENG Jing,JIANG Jian-jing,XIAO Ru-cheng,et al.Stdudy of the mechanish of aerostatics instability for long_span bridge[J].China Civil Engineering Journal,2002,35(1):35-39.
[6]程 进,肖汝诚,项海帆.大跨径悬索桥静风稳定性的参数研究.公路交通科技,2001,18(2),29-32.
CHENG Jing,XIAO Ru-cheng,XIANG Hai-fan.Parametric studies on aerostatics stability for suspension bridge[J].Journal of Highway And Transportatio n Research And Development,2001,18(2),29-32.
[7]李加武,陈 飞,张宏杰.考虑雷诺数效应的桥梁静风稳定分析.公路交通科技,2009,26(5):64-74.
LI Jia-wu,CHEN Fei,ZHANG Hong-jie.Analysis of static_wind stability of bridge with consideration of reynolds numbers effects[J].Journal of Highway And Transportation Research And Development,2009,26(5):64-74.
[8]胡晓伦.大跨度斜拉桥颤抖振响应及静力稳定性分析[D].上海:同济大学,2006.
[9]张志田,葛耀君.大跨度悬索桥非线性静风稳定精细化分析[A].第十六届全国桥梁学术会议论文集[C].2004.
[10]李永乐,欧阳韦,郝 超,等.大跨度悬索桥静风失稳形态及机理研究[J].空气动力学学报,2009,27(6):701-706.
LI Yong-le,OUYANG Wei ,HAO Chao,et al.Study on shape for long-span susoension bridges[J].Acta Aero Dynamica Sinica,2009,27(6):701-706.
