影响从涡激振动中获取能量的参数研究

罗竹梅，张立翔

(1．昆明理工大学 能源与动力工程系，昆明 650093；2.昆明理工大学 工程力学系，昆明 650051)

目前对海流能的利用主要集中在潮流能利用方面，即利用水下涡轮发电装置从具有较大流速的潮流中获取能量，但基于涡激振动从海洋流或河流中获取能量方面的研究很少[1-3]。非流线形结构在水流作用下会在其两侧产生周期性的旋涡脱落，从而在结构上形成与流向垂直的周期性外力，引发结构横向振动，即通常所说的涡激振动。涡激振动其共振发生在固有频率附近一定范围内，在较广的流速和雷诺数范围内，都能产生有效的振动，即使在低速的水流中也可获得横向的水动能。水下涡轮机在2.5～3.6 m/s甚至更高的流速下才可以工作，而全世界大量的海洋流其流速都低于1.5 m/s，一般河流其水流速度低于1.03 m/s。因此这一想法对于从低速河流和海流中获取能量具有重要的现实意义。

利用涡激振动从低速水流中获取能量的研究还停留在理论和实验阶段。Bernitsas[4-6]的团队仅对单个弹性支撑刚性圆柱体的涡激振动进行了研究，主要研究了自由表面、雷诺数、阻尼比及表面粗糙度的设计对圆柱体振幅和共振范围的影响。圆柱体质量比m*(m*为振动体质量与排开流体质量之比)、阻尼比ζ、质量阻尼比m*ζ以及圆柱体在水中的固有频率fn对从水流中获取能量效率η的影响，目前相关文献报道极少。受物理实验条件的限制，本文通过流固充分耦合的数值方法，对二维弹性支撑圆柱体在均匀流中的横向涡激振动进行了模拟。并用该数值方法进行了4种方案计算，以观察m*、ζ、m*ζ和fn对η的影响。

1 涡激振动数值模拟

1.1 流体模型

流体控制方程用非定常不可压缩雷诺平均N-S方程求解并用SST(Shear-Stress Transport)k-ω湍流模型封闭。为保证圆柱大位移运动时流体网格的质量，采用任意拉格朗日欧拉(Arbitrary Lagrange-Euler，ALE)方法。ALE描述下流体的连续性方程和动量方程

(1)

(2)

(3)

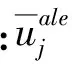
采用有限元中的有限体积法对方程组进行离散，流体区域采用非结构四边形网格，压力-速度耦合方式采用PISO算法，空间导数采用二阶精度的中心差分格式，压力差值选择标准方法，时间导数用二阶组合时间积分法。

1.2 结构模型

假定圆柱体被置于一个质量-弹簧-阻尼系统中，如图1所示。

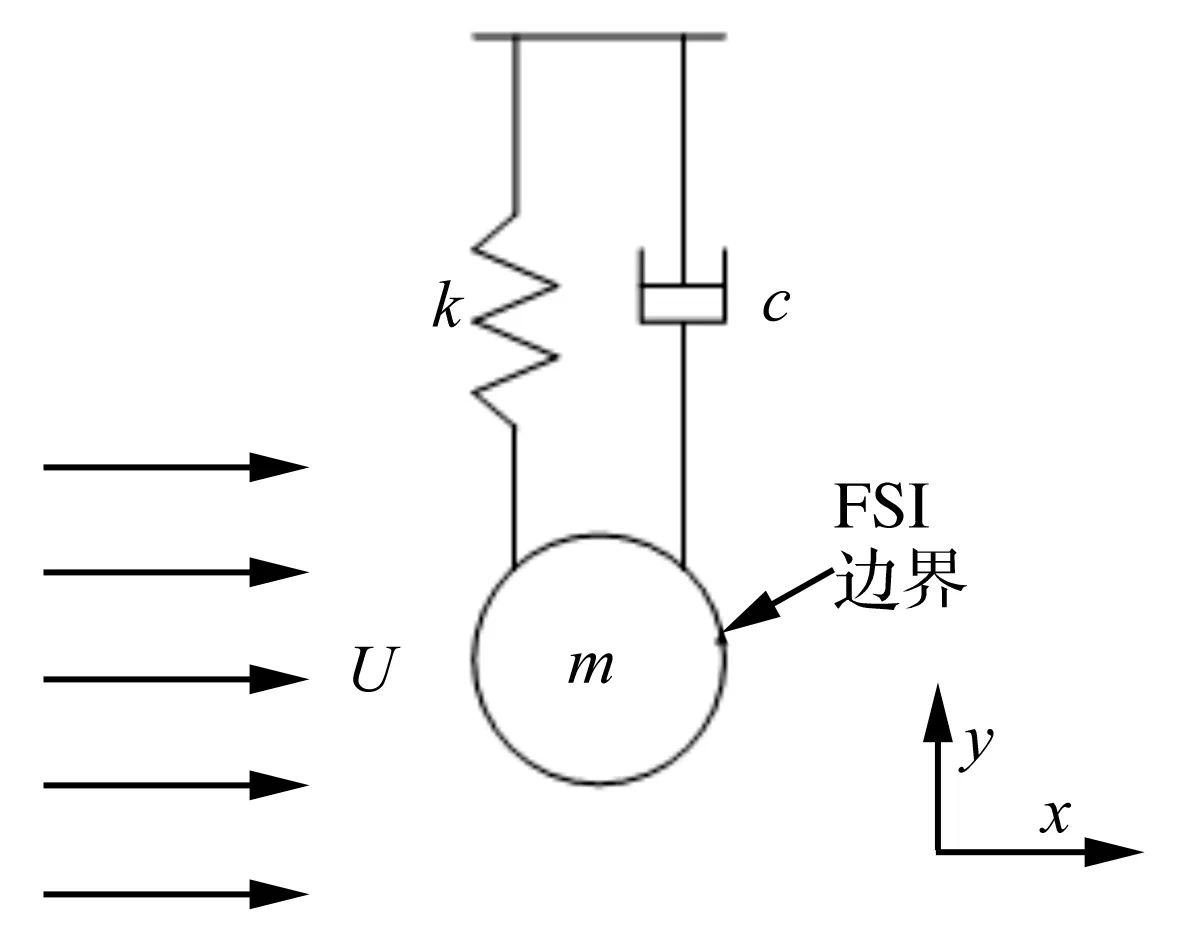
图1 圆柱体涡激振动模型

结构控制方程采用有限元数值离散方法，离散后的非线性方程组写成矩阵形式

(4)

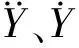
1.3 涡激振动模拟

流体和固体模型建好后，通过流固耦合求解器同时耦合求解，耦合边界上应用位移协调条件、力平衡条件以及速度平衡条件。每个时间步内进行多次迭代计算，直到满足计算精度，流体和结构才整体向前推进计算。这一数值方法实现了流体和结构充分耦合计算，可模拟真实的涡激振动现象。

为了验证本数值方法的合理性，采用与Guilmineau等[7]数值实验及Khalak等[8]的物理实验完全相同的低质量比m*=2.4和质量阻尼比m*ζ=0.013。对振幅A、流速U和激励频率fex进行无量纲化处理：A*=A/D，U*=U/fnD，f*=fex/fn，其中A*、U*和f*分别为圆柱体振幅比、约化速度和频率比，实验结果如图2所示。

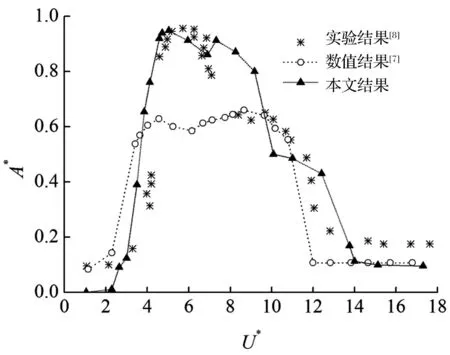
图2 不同实验中的振幅比A*

2 能量获取效率η

共振范围内，圆柱体横向位移响应为定常态的谐波振动，呈正弦规律变化，且与升力之间存在一个相位差Φ，因此，可将单位长度圆柱体横向位移y(t)和升力Fy表达成

y(t)=Asin(2πfext)

(5)

(6)

式中:Cy为升力系数幅值；D代表圆柱体直径。

能量转换效率η的大小可根据流体在一个振动周期内对单位长度的圆柱体做功的大小Ps与单位长度内流体的总能量Pf之比进行计算，即：η=Ps/Pf。其中，单位时间内单位长度流体的总能量

(7)

单位时间单位长度圆柱体从流体中获取能量

(8)

结合式(5)～(8)，采用如下无量纲形式表达能量获取效率η

η=πA*CysinΦ(f*/U*)

(9)

3 结 果

约化速度U*的计算范围为3～13，这一范围包含了实验中出现的整个共振范围。用本文数值方法进行了大量的数值计算，计算方案见表1。

表1 实验方案

式(9)中各参数值可通过数值计算结果直接或间接得到，其中相位差Φ用过零鉴相法求得：在特定时刻，求解两个信号通过零点的时间差Δt，根据参考信号的频率ω，得出相位差Φ=180ωΔt/π，然后确定相位差Φ的符号。

3.1 m*和ζ对η的影响

为考察m*和ζ对横向能量获取效率η的影响，设计了两组方案：第一组方案固定m*、fn，通过改变ζ以观察ζ对η的影响;第二组方案则固定ζ、fn，通过改变m*以观察m*对η的影响，见表1中方案1和方案2。

弹性支撑刚性圆柱体峰值振幅的大小取决于m*ζ，m*ζ越小，振幅峰值越大[8-10]。m*对涡激振动横向位移的影响是非线性的，而结构阻尼比ζ的影响则几乎是线性的[11]。方案1的计算结果见图3。

图4中可以观察到方案2下m*对η的影响趋势：m*=2时，其能量获取效率的峰值ηmax最小，为0.195，但从水流中有效获取能量的约化速度最广；m*=4时，其能量获取效率的峰值ηmax最大，为0.262，相反，其从水流中有效获取能量的约化速度范围最窄。这说明m*不仅影响能量获取效率的大小，同时也影响有效获取能量的约化速度范围。

图3 方案1中A*和η随U*的变化图

3.2 m*ζ对η的影响

从方案1的实验结果不难发现，当m*ζ=0.21时，其ηmax出现最大值。为了观察其它质量阻尼比m*ζ下圆柱体从涡激振动中获取能量的效率，增加了方案3，见表1。如图5所示，当m*=2，m*ζ=0.24时，其ηmax值远高于其它两种阻尼比下的值，ηmax达到0.301，其它两种情况的ηmax值相当，约为0.2。

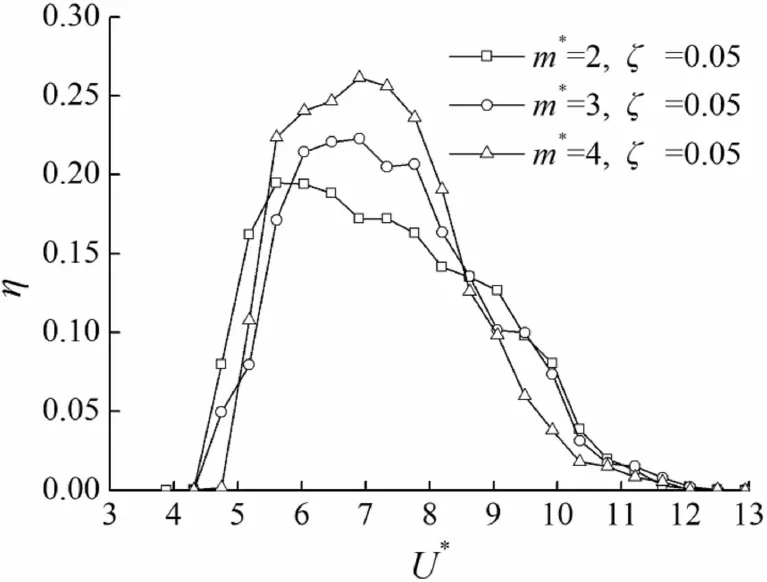
图4 方案2中η随U*的变化图

图5 方案3中η随U*的变化图

图6 m*ζ与η的关系图

此外，在方案1的基础上，增加了更小阻尼比ζ=0.01下的涡激振动响应计算。将组合参数m*ζ值(0.03、0.1、0.15、0.2、0.21、0.24、0.3、0.4)及其对应的ηmax值进行整理，发现m*ζ控制ηmax值的大小，且存在一个最优的m*ζ，使圆柱体从涡激振动中获取能量的效率最大。对共振范围内各m*ζ值下的η求平均值，发现最大平均效率ηp也出现在m*ζ=0.24处，如图6所示。因此，在某一雷诺数范围内，选取合理的质量阻尼比m*ζ，可使圆柱体从涡激振动中获取能量的峰值效率ηmax及平均效率η最大。

3.3 fn对η的影响

图7 方案4中A*随U及η随U*的变化图

随着fn的增加，其峰值振幅先增加后又减小，但其共振范围却向高流速和高雷诺数移动，这一点对从涡激振动中获取能量很重要。与fn对峰值振幅的影响规律一样，随着fn的增加，其ηmax值也是先增加后减小，但有效获取能量的约化速度范围却随着fn的增加逐渐减小。从方案4的实验结果图7来看，适当选取fn值，可使圆柱体从涡激振动中获取能量的效率最大，且同时还可拥有较广的速度范围。

4 结 论

本文通过流固充分耦合数值方法模拟涡激振动，并用该数值方法对影响弹性支撑圆柱体从涡激振动中获取能量的参数进行了研究。设计了4种方案来分析m*、ζ、m*ζ和fn对获取能量效率η的影响。通过对实验数据进行分析，得到如下结论：

(1)m*不仅影响η的大小，同时也影响有效获取能量的约化速度范围。当m*不变时，存在一个最优的ζ值使圆柱体从涡激振动中获取能量的效率最大。因此，为了能在较大的速度范围内有效地从海洋流或河流中获取能量，建议采用较低的m*，但为了得到更大的ηmax，需选择一个合理的阻尼比ζ。

(2)m*ζ控制获取能量的最大效率ηmax和平均效率ηp的大小，且存在一个最优的m*ζ，可使ηmax和ηp最大。

(3)适当选取fn，可使圆柱体从涡激振动中获取能量的效率最大，同时还可使其应用速度范围较广。

对从海洋流或河流中利用涡激振动获取能量的振动系统设计，本实验结果可提供参考。

[1]Barrero-Gil A，Alonso G，Sanz-Andres A.Energy harvesting from transverse galloping[J].Journal of Sound and Vibration，2010，329 (14):2873-2883.

[2]Bernitsas M M，Raghawan Y，Ben-Simon E M H，et al.VIVACE (vortex induced vibration for aquatic clean renewable energy from fluid flow[J].Journal of Offshore Mechanics and Arctic Engineering，2008，130: 041101.

[3]Yoshiki，Nishi.Power extraction from vortex-induced vibration of dual mass system[J].Journal of Sound and Vibration，2012:1-14.

[4]Bernitsas M M，Ben-Simon Y，Raghavan K，et al.The VIVACE converter: model tests at high damping and Reynolds number around105[J].Journal of Offshore Mechanics and Arctic Engineering，2009，131:011102.

[5]Raghavan K，Bernitsas M M.Experimental investigation of Reynolds number effect on vortex induced vibration of rigid circular cylinder on elastic supports[J].Ocean Engineering，2011,38:719-731.

[6]Lee J H，Bernitsas M M.High-damping，high-Reynolds VIV tests for energy harnessing using the VIVACE converter[J].Ocean Engineering 2011,38: 1697-1712.

[7]Guilmineau E，Queutey P.Numerical simulation of vortex-induced vibration of a circular cylinder with low mass-damping in a turbulent flow[J].Journal of Fluids and Structures，2004，19: 449-466.

[8]Khalak A，Williamson C H K.Motions，forces and mode transitions in vortex-induced vibration at low mass-damping[J].Journal of Fluids and Structures，1999，13: 813-851.

[9]范杰利，黄维平.细长立管两向自由度涡激振动数值研究[J].振动与冲击，2012，31(24)：65-68.

FAN Jie-li，HUANG Wei-ping.Numerical simulation of 2-DOF vortex-induced vibration of a long riser[J].Journal of Vibration and Shock，2012，31(24)：65-68.

[10]Govardhan R，Williamson C H K.Modes of vortex formation and frequency response of a freely vibrating cylinder[J].Journal of Fluids Mechanics，2000，420: 85-130.

[11]何长江，段忠东.二维圆柱涡激振动的数值模拟[J].海洋工程，2008，26:57-63.

HE Chang-jiang，DUAN Zhong-dong.Numerical simulation of two-dimensional cylindrical vortex-induced vibration[J].Journal of Ocean Engineering，2008，26:57-63.